引言
我们想一想计算机如何执行决策任务?当音乐应用推荐歌曲、电商平台建议商品,或银行系统处理贷款申请时,这些功能常依赖于一种算法进行决策。今天,我们将学习机器学习中的一种基本算法:决策树。它通过一系列规则对数据进行分类或预测,结构直观且易于理解。决策树会从数据中学习规则,并按照特征逐层划分,最终输出决策结果。
一、认识决策树------像树一样思考
1、什么是决策树
决策树是一种模拟人类逐步推理过程的经典机器学习算法,它通过构建一棵由节点和分支组成的树状结构,依据数据特征按层级进行规则判断,实现对样本的分类或回归预测,它的核心组件包括:根节点(代表整个数据集的起始判断点)、内部节点(每个节点对应一个特征属性的测试条件,将数据划分到不同分支)、叶子节点(位于树末端,代表最终的分类结果或预测值)以及连接它们的分支(表示基于判断条件所导向的不同路径),让我来举一个简单的银行贷款例子:
房产?
/ \
无 有
/ \
车辆? 可以贷款
/ \
无 有
/ \
不可贷款 车收入?
/ \
>30万 <30万
/ \
可以贷款 不可贷款这个树告诉我们有房产的直接可以贷款,没房产但有车的,则是由收入决定的,没房产也没车的,不能贷款。
2、决策树能做什么?
决策树可以胜任两种预测任务:分类任务:预测离散的类别标签,例如判断电信客户是否会流失(是/否)、识别一封邮件是否为垃圾邮件、或辅助进行疾病诊断(健康/患病),以及回归任务:预测连续的数值结果,例如预估房价、 forecasting 销售额或分析温度变化趋势。通过其基于规则的树形结构,决策树能够从数据特征中学习并模拟出复杂的决策边界或函数关系,使其在商业、医疗、金融等多个领域都有广泛的应用。
二、决策树的"灵魂"------三种核心算法
1、ID3算法:用"不确定性"衡量
ID3算法是一种经典的决策树生成算法,它是利用"不确定性"的减少来指导特征选择。它使用信息熵作为衡量数据集混乱程度的指标,熵值越大,表示数据的类别分布越混杂、不确定性越高。熵的计算公式为:H(U) = -Σ(p_i * log₂(p_i)),(其中p_i是第i类样本的比例。)。举一个简单的例子:假设我们有14天的数据,9天打球,5天不打球:信息增益 = 分裂前的熵 - 分裂后的加权平均熵,信息增益越大,说明用这个特征分裂效果越好。
import math
# 计算熵值
p_play = 9/14
p_not_play = 5/14
entropy = -p_play * math.log2(p_play) - p_not_play * math.log2(p_not_play)
print(f"熵值: {entropy:.3f}")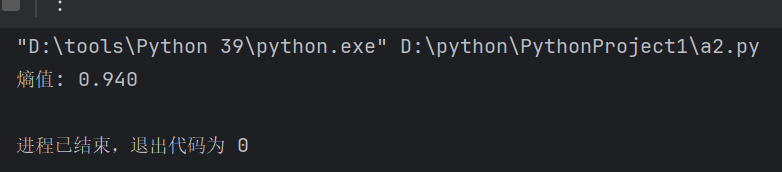
2、C4.5算法:解决ID3的缺陷
ID3 存在的一个关键缺陷:由于 ID3 单纯依据信息增益来选择分裂特征,它会天然地偏好那些取值数量众多的特征,因为这类特征往往能产生非常纯的子集,带来很高的信息增益,但这会导致模型过拟合,缺乏泛化能力。C4.5算法是对 ID3 算法的一项重要改进:它引入了信息增益率作为新的特征选择标准,其定义为信息增益除以该特征本身的固有熵。即便一个特征取值很多、信息增益高,但如果它自身的熵也很大(表示其取值分布本身就很混乱),那么其信息增益率就会被抑制,从而更公平地评估特征的真实分类能力。
3、CART算法:最常用的现代算法
CART算法是目前广泛应用的决策树生成算法,其特点是能够同时处理分类与回归任务:在解决分类问题时,它使用基尼系数(Gini Index)作为衡量节点纯度的分裂标准,而在解决回归问题时,则使用均方误差(MSE)作为分裂标准。对于二分类问题,基尼系数的计算公式为Gini = 2 * p * (1-p),(其中p是正例的比例),基尼系数直观地反映了数据集的"不纯度",其值域在0到0.5之间(对于二分类),系数值越小,表示节点内样本的类别越趋于一致,即"纯度"越高,因此,CART算法在每一步分裂时,都会选择那个能使子节点加权基尼系数(或回归问题的均方误差)下降最多的特征及其分割点,通过这种递归的二分方式构建出一棵有强大预测能力的决策树。
三、实战:用Python构建第一棵决策树
1、环境准备
首先确保安装了必要的库:
pip install pandas scikit-learn matplotlib numpy2、电信客户流失预测实战
1.导入必要的库
import pandas as pd # 数据处理和分析
import numpy as np # 数值计算
import matplotlib.pyplot as plt # 数据可视化
from sklearn.model_selection import train_test_split # 数据集划分
from sklearn.tree import DecisionTreeClassifier, plot_tree # 决策树模型和可视化
from sklearn import metrics # 模型评估指标2.数据加载
data = pd.read_excel("电信客户流失数据.xlsx")3.数据预处理
# 特征和目标变量分离
X = data.iloc[:, :-1]
y = data.iloc[:, -1]
# 数据集划分(80%训练,20%测试)
# stratify=y 确保训练集和测试集中正负样本比例一致
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42, stratify=y
)4.决策树模型构建
clf = DecisionTreeClassifier(
criterion='gini', # 使用基尼系数作为分裂标准(CART算法)
max_depth=3, # 限制树的最大深度,防止过拟合
min_samples_split=10, # 节点至少需要10个样本才考虑分裂
min_samples_leaf=5, # 叶节点至少包含5个样本
random_state=42 # 确保结果可复现
)5.模型训练与可视化
clf.fit(X_train, y_train) # 训练模型
# 可视化决策树
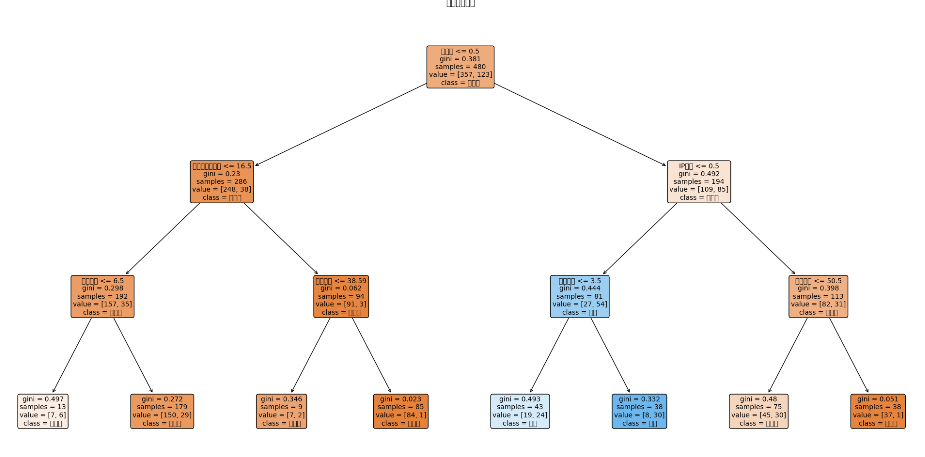
plt.figure(figsize=(20, 10))
plot_tree(clf,
feature_names=X.columns, # 显示特征名
class_names=['未流失', '流失'], # 类别标签
filled=True, # 用颜色填充节点
rounded=True, # 圆角边框
fontsize=10,
proportion=True) # 显示样本比例而不是数量6.模型评估
# 预测
y_pred = clf.predict(X_test)
y_pred_proba = clf.predict_proba(X_test)[:, 1] # 预测为流失的概率
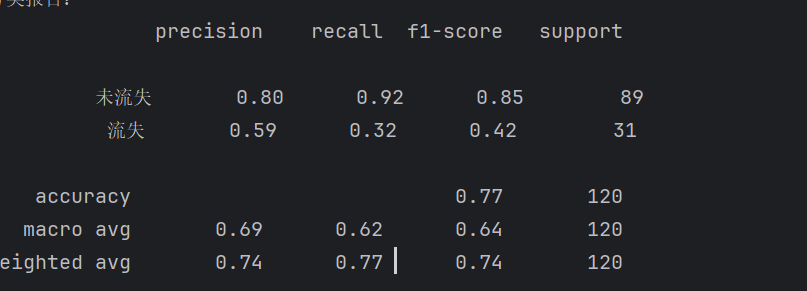
# 分类报告
print("分类报告:")
print(metrics.classification_report(y_test, y_pred, target_names=['未流失', '流失']))
# 混淆矩阵
cm = metrics.confusion_matrix(y_test, y_pred)
print("混淆矩阵:")
print(cm)7.绘制AUC-ROC曲线
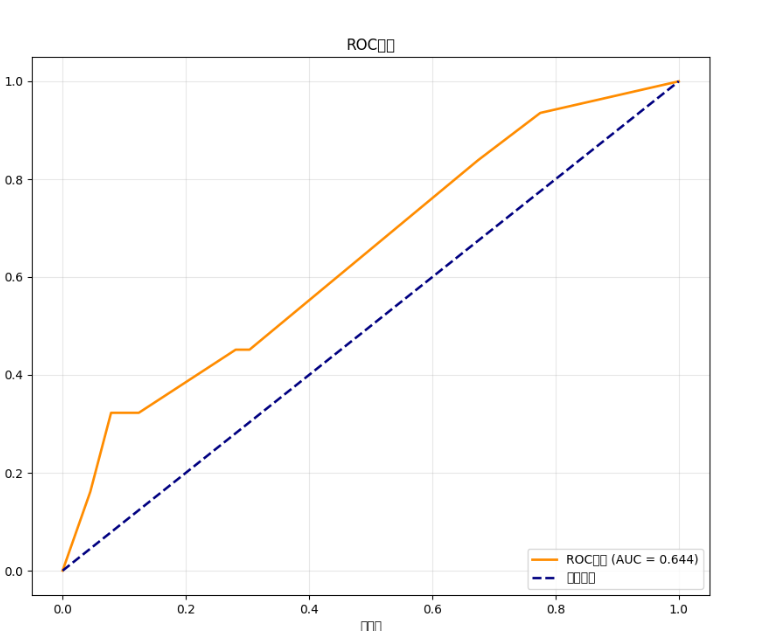
fpr, tpr, thresholds = metrics.roc_curve(y_test, y_pred_proba)
roc_auc = metrics.auc(fpr, tpr)
plt.figure(figsize=(10, 8))
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC曲线 (AUC = {roc_auc:.3f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--', label='随机猜测')
plt.xlabel('假正率')
plt.ylabel('真正率')
plt.title('ROC曲线')
plt.legend(loc="lower right")
plt.grid(True, alpha=0.3)
plt.show()8.运行代码
四、决策树的深度探索
1、回归树:预测连续值
-
导入必要库
import numpy as np
from sklearn.tree import DecisionTreeRegressor, plot_tree
import matplotlib.pyplot as plt
2.创建示例数据
# 设置随机种子,确保每次运行结果相同
np.random.seed(42)
# 创建100个样本,3个特征
X_reg = np.random.rand(100, 3) * 100 # 特征值范围:0-100
# 创建目标变量(房价)
y_reg = 50 + X_reg[:,0]*0.3 + X_reg[:,1]*20 + X_reg[:,2]*0.5 + np.random.randn(100)*10我们通过np.random.seed(42) 设置随机种子以确保结果的可重复性,随后生成了一个包含100个样本且每个样本具有3个特征的特征矩阵 X_reg,其值在0到100之间均匀随机生成,分别模拟房屋的面积(平方米)、房间数量(个)和地理位置得分,目标变量 y_reg(代表房价)则由一个预设的线性关系生成:基础房价50加上面积乘以0.3、房间数乘以20、地理位置得分乘以0.5的贡献,最后再添加一个标准差为10的正态分布随机噪声项,来模拟现实数据中的不确定性。
-
创建回归树模型
创建回归树
reg_tree = DecisionTreeRegressor(
criterion='squared_error', # 分裂标准:均方误差
max_depth=3, # 最大深度为3层
min_samples_leaf=5, # 叶节点最少5个样本
random_state=42 # 确保可重复性
) -
训练模型
用数据训练回归树
reg_tree.fit(X_reg, y_reg)
获取模型得分
score = reg_tree.score(X_reg, y_reg)
print(f"模型R²分数: {score:.3f}")
5.可视化决策树
# 设置图形大小
plt.figure(figsize=(12, 6))
# 绘制决策树
plot_tree(reg_tree,
feature_names=['面积', '房间数', '地理位置'],
filled=True, # 填充颜色
rounded=True, # 圆角矩形
fontsize=10) # 字体大小
# 添加标题
plt.title("房价预测回归树", fontsize=14)
# 显示图形
plt.tight_layout()
plt.show()6.运行代码

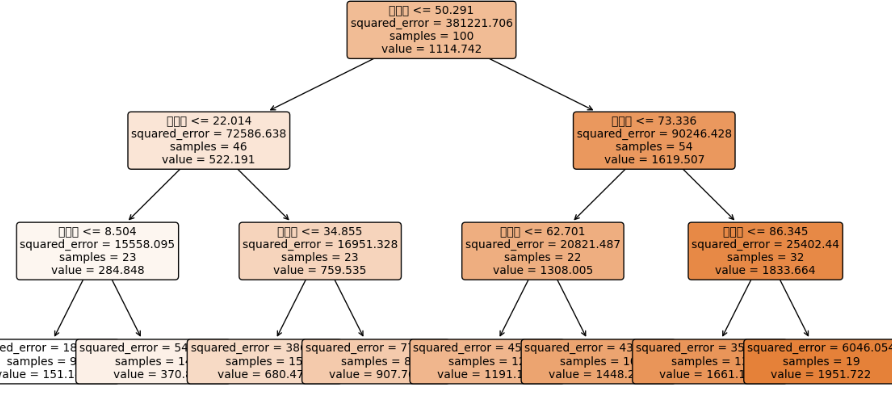
2、关键参数详解与调优
1.导入库和初始化模型
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeClassifier
# 创建基础决策树模型
base_tree = DecisionTreeClassifier(random_state=42)2.定义搜索参数
# 简化的参数网格(为了加速搜索)
simple_grid = {
'max_depth': [3, 4, 5], # 树的最大深度
'min_samples_leaf': [5, 10, 20] # 叶子节点最少样本数
}在通过网格搜索进行决策树模型的超参数调优时,我们定义了一个简化的参数网格 simple_grid来提升搜索效率,其中重点关注两个关键参数:其一是 max_depth,它用于控制树的最大生长深度,防止模型过度复杂,本次搜索将其候选值设定为 [3, 4, 5];其二是 min_samples_leaf,它规定了叶节点所需的最小样本数,有助于避免过拟合,本次搜索的候选值为 [5, 10, 20]。通过这个精炼的参数组合,系统可以更高效地遍历并评估不同模型配置的性能。
3.执行网格搜索
# 创建网格搜索对象
grid_search = GridSearchCV(
base_tree, # 基础模型
simple_grid, # 参数网格
cv=5, # 5折交叉验证
scoring='roc_auc' # 使用AUC评分
)
# 在训练数据上执行搜索
grid_search.fit(X_train, y_train)为了寻找决策树模型的最优参数组合,我们首先创建一个 GridSearchCV 对象,该对象以基础决策树模型为估计器,并传入之前定义的简化参数网格,同时指定使用交叉验证来评估每一组参数的稳健性,并以ROC曲线下面积作为模型优劣的评分标准,随后,调用该对象的 fit 方法在训练集 (X_train, y_train) 上执行全面的网格搜索,最终确定出在验证集上表现最佳的参数配置。
4.获取最佳模型
# 获取最佳参数
best_params = grid_search.best_params_
# 获取最佳模型
best_tree = grid_search.best_estimator_
# 使用最佳参数重新训练模型(确保完全拟合)
best_tree.fit(X_train, y_train)5.性能评估与比较
from sklearn import metrics
# 使用调优后的模型预测
y_pred_best = best_tree.predict(X_test)
# 计算调优后准确率
best_accuracy = metrics.accuracy_score(y_test, y_pred_best)
# 计算原始模型准确率(假设已有模型clf)
original_accuracy = metrics.accuracy_score(y_test, clf.predict(X_test))为了评估经过网格搜索调优后的决策树模型的性能,将其与未经调优的原始模型进行比较,我们首先使用调优得到的最佳模型对测试集进行预测,得到预测标签,随后,利用 accuracy_score 函数计算该最佳模型在测试集上的分类准确率,同时,为了进行对比,我们也计算出预先训练好的原始模型 clf 在相同测试集上的准确率,从而能够评估参数调优过程对模型性能的提升效果。
6.输出结果
print(f"最佳参数: {best_params}")
print(f"最佳交叉验证AUC: {grid_search.best_score_:.3f}")
print(f"\n性能对比:")
print(f"调优前准确率: {original_accuracy:.3f}")
print(f"调优后准确率: {best_accuracy:.3f}")
print(f"提升: {(best_accuracy-original_accuracy)*100:.1f}%")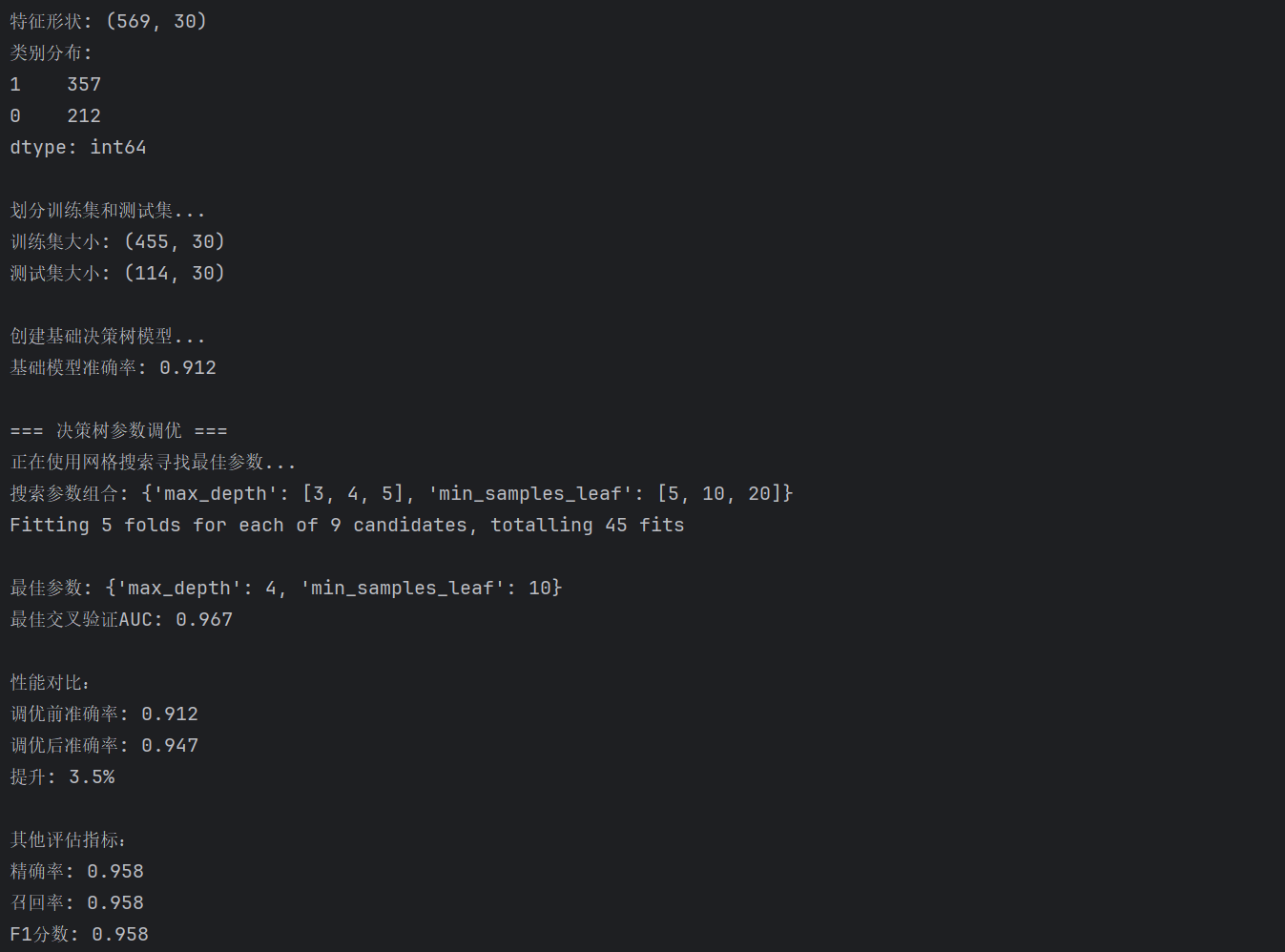
到这里我们就学完了决策树算法的基本内容了,在下一章里我们将继续学习机器学习中其他的一些常用算法。