引言:学习的本质是什么?
在人工智能的发展历程中,一个核心问题始终萦绕不去:机器如何学会理解数据的内在结构? 人类能从几个像素识别一张脸,能从几个音符听出一段旋律,能从几个词语理解一段情感。这种从有限信息中理解整体的能力,正是表示学习的核心目标。
自编码器(Autoencoder)和变分自编码器(Variational Autoencoder)就是在这种背景下诞生的两种重要模型。它们不仅是深度学习中的重要组成部分,更是通往智能生成 和理解学习的关键桥梁。
一、 基本概念
想象一下,当你需要向朋友描述一张复杂的图片时,你会怎么做?你可能会说:"这是一张猫的图片,橘色条纹,坐在窗台上,窗外是城市夜景。" 你并没有传输整张图片的数百万个像素,而是用几十个词压缩 了关键信息,而这些信息足够让朋友在脑海中重建出大致的画面。
这就是自编码器的核心思想:学习数据的有效表示。
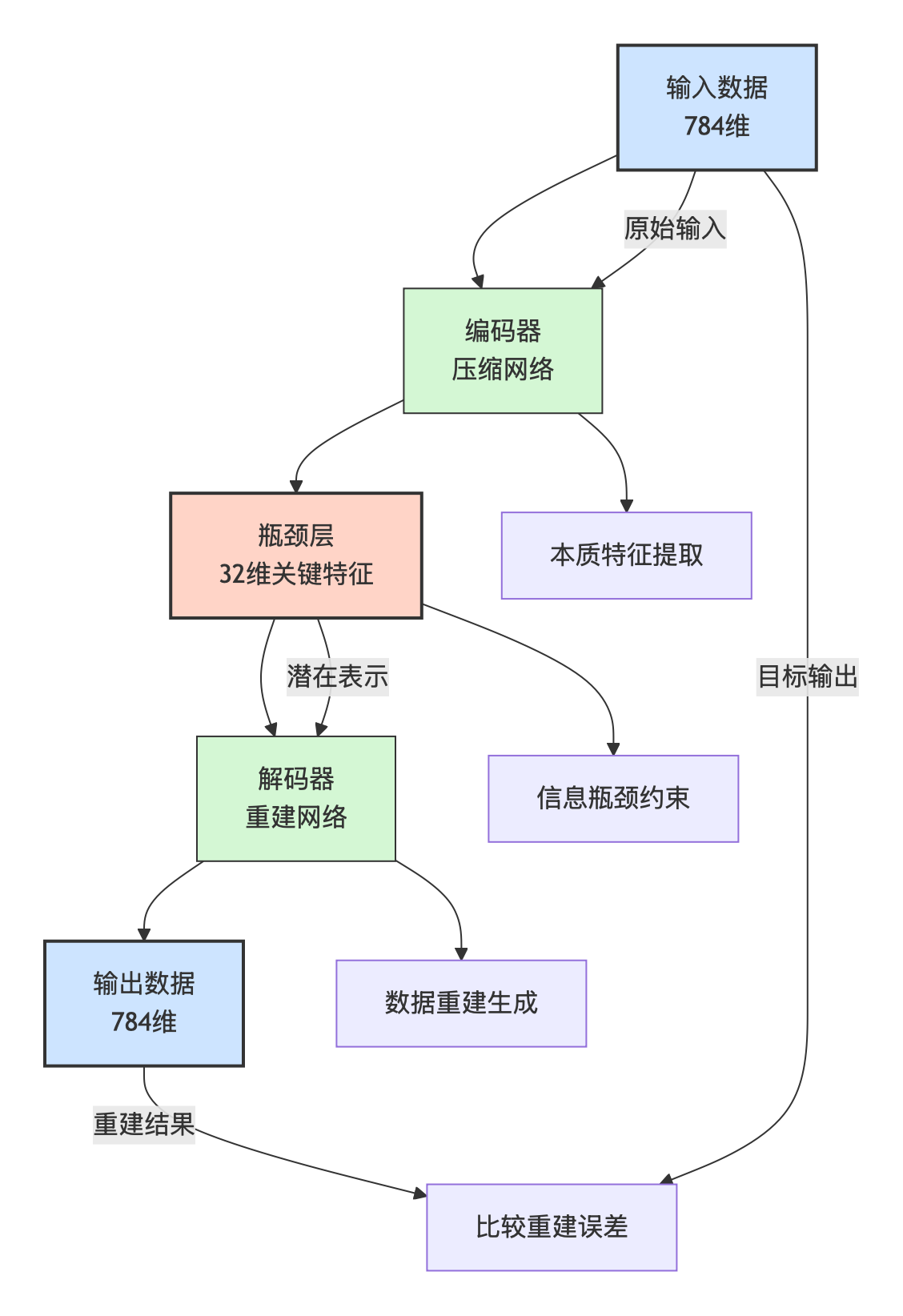
二、技术原理:压缩与重建
自编码器的目标是学习一个函数,使得:
f(x)=decoder(encoder(x))≈x f(x) = \text{decoder}(\text{encoder}(x)) \approx x f(x)=decoder(encoder(x))≈x
这看似同义反复的过程,却通过瓶颈约束 实现了奇妙的效果。当信息必须通过一个维度远小于输入的瓶颈时,网络被迫选择性地记忆最重要的特征。
假设我们要处理 28×28 像素的手写数字图片(784 维),瓶颈层设为 32 维,那么:
- 原始:784个像素
- 压缩后:32个关键特征
这 32:1 的压缩比 迫使网络学习 什么是数字的本质 :是笔画的方向、曲线的弧度、结构的比例,而不是具体的像素位置。数学表达 很简单:
设编码器函数为 EEE,解码器函数为DDD,则:
潜在表示: z=E(x)z = E(x)z=E(x)
重建输出: x′=D(z)=D(E(x))x' = D(z) = D(E(x))x′=D(z)=D(E(x))
损失函数: L=∣∣x−x′∣∣2L = ||x - x'||^2L=∣∣x−x′∣∣2
三、自编码器重建MNIST手写数字
- 输入层:784 维(28×28 像素的手写数字图像)
- 编码器:逐层压缩输入数据,最终得到 32 维的瓶颈层表示
- 解码器:逐层重建数据,输出与输入相同维度的图像
- 自编码器通过学习数据的有效表示,能够提取出重要的特征,从而实现数据的压缩和重建。
python
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
torch.manual_seed(42)
device = torch.device("mps" if torch.backends.mps.is_available() else "cuda" if torch.cuda.is_available() else "cpu")
print(f"使用设备: {device}")
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)) # 将像素值归一化到[-1, 1]
])
train_dataset = torchvision.datasets.MNIST(
root='./data', train=True, download=True, transform=transform
)
test_dataset = torchvision.datasets.MNIST(
root='./data', train=False, download=True, transform=transform
)
batch_size = 256
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
class SimpleAutoencoder(nn.Module):
"""
简单的全连接自编码器
结构: 784(输入) → 256 → 128 → 32(瓶颈层) → 128 → 256 → 784(输出)
"""
def __init__(self):
super(SimpleAutoencoder, self).__init__()
# 编码器
self.encoder = nn.Sequential(
nn.Linear(784, 256),
nn.ReLU(True),
nn.Linear(256, 128),
nn.ReLU(True),
nn.Linear(128, 32), # 瓶颈层,32维压缩表示
nn.ReLU(True)
)
# 解码器
self.decoder = nn.Sequential(
nn.Linear(32, 128),
nn.ReLU(True),
nn.Linear(128, 256),
nn.ReLU(True),
nn.Linear(256, 784),
nn.Tanh() # 输出值在[-1, 1]之间,匹配输入归一化
)
def forward(self, x):
x_flat = x.view(x.size(0), -1)
encoded = self.encoder(x_flat)
decoded = self.decoder(encoded)
reconstructed = decoded.view(x.size(0), 1, 28, 28)
return reconstructed, encoded
model = SimpleAutoencoder().to(device)
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
def train_autoencoder(model, train_loader, num_epochs=20):
model.train()
for epoch in range(num_epochs):
epoch_loss = 0.0
for batch_idx, (data, _) in enumerate(train_loader):
data = data.to(device)
# 前向传播
reconstructed, _ = model(data)
loss = criterion(reconstructed, data)
# 反向传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
epoch_loss += loss.item()
avg_loss = epoch_loss / len(train_loader)
# 打印每个epoch的损失
print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {avg_loss:.6f}')
print("开始训练自编码器...")
num_epochs = 20
train_autoencoder(model, train_loader, num_epochs)
def visualize_reconstructions(model, test_loader, num_examples=8):
model.eval()
with torch.no_grad():
data_iter = iter(test_loader)
images, labels = next(data_iter)
images = images.to(device)
reconstructed, _ = model(images)
images = images.cpu()
reconstructed = reconstructed.cpu()
images = (images + 1) / 2
reconstructed = (reconstructed + 1) / 2
fig, axes = plt.subplots(2, num_examples, figsize=(15, 4))
for i in range(num_examples):
axes[0, i].imshow(images[i].squeeze(), cmap='gray')
axes[0, i].set_title(f'Label: {labels[i]}')
axes[0, i].axis('off')
axes[1, i].imshow(reconstructed[i].squeeze(), cmap='gray')
axes[1, i].set_title('Reconstructed')
axes[1, i].axis('off')
plt.tight_layout()
plt.show()
return images, reconstructed
original_imgs, reconstructed_imgs = visualize_reconstructions(model, test_loader)
def evaluate_reconstruction_quality(original, reconstructed):
"""计算重建图像的质量指标"""
mse = np.mean((original.numpy() - reconstructed.numpy()) ** 2)
psnr = 20 * np.log10(1.0 / np.sqrt(mse)) # 峰值信噪比
print(f"重建质量评估:")
print(f"均方误差 (MSE): {mse:.6f}")
print(f"峰值信噪比 (PSNR): {psnr:.2f} dB")
return mse, psnr
evaluate_reconstruction_quality(original_imgs[:8], reconstructed_imgs[:8])
python
重建质量评估:
均方误差 (MSE): 0.008786
峰值信噪比 (PSNR): 20.56 dB
四、自编码器的变体
稀疏自编码器
目标:让少数神经元在给定输入时被激活,模仿大脑的稀疏编码。
核心思想:在损失函数中添加稀疏性约束:
L=∣∣x−x′∣∣2⏟重建损失+λ∑j∣aj∣⏟稀疏性约束 L = \underbrace{||x - x'||^2}{\text{重建损失}} + \lambda \underbrace{\sum{j} |a_j|}_{\text{稀疏性约束}} L=重建损失 ∣∣x−x′∣∣2+λ稀疏性约束 j∑∣aj∣
- aja_jaj 是瓶颈层神经元的激活值
- λ\lambdaλ 控制稀疏性的强度
- 使用 L1 正则化鼓励神经元在大部分时间保持静默
效果:每个神经元变得"专业化",只对特定特征敏感,学习到更可解释的特征。
去噪自编码器
目标 :从有噪声的输入重建干净数据,学习数据的本质结构。
核心思想 :对输入添加噪声 ϵ\epsilonϵ,让模型重建原始干净数据:
L=E[∣∣x−D(E(x+ϵ))∣∣2]L = \mathbb{E} \left[ ||x - D(E(x + \epsilon))||^2 \right]L=E[∣∣x−D(E(x+ϵ))∣∣2]
- ϵ\epsilonϵ 可以是高斯噪声、遮挡噪声等
- 网络不能简单记忆,必须理解数据的统计规律
- 增强模型的鲁棒性和泛化能力
效果:模型学会忽略噪声,抓住数据的本质特征,能处理不完美的输入。
收缩自编码器
目标 :使编码对输入的微小变化不敏感,学习更稳定的特征。
核心思想 :惩罚编码对输入变化的敏感度:
L=∣∣x−x′∣∣2+λ∑i,j(∂zj∂xi)2L = ||x - x'||^2 + \lambda \sum_{i,j} \left( \frac{\partial z_j}{\partial x_i} \right)^2L=∣∣x−x′∣∣2+λi,j∑(∂xi∂zj)2
- ∂zj∂xi\frac{\partial z_j}{\partial x_i}∂xi∂zj 是潜在变量对输入变化的敏感度
- 鼓励相似输入产生相似编码
- 防止过拟合,提高特征稳定性
效果:学习到对输入微小扰动不敏感的特征,提高模型的鲁棒性。