5. pytorch第一个神经网络

pytorch第一个神经网络

文章目录

pytorch第一个神经网络
- 前言
- [1. 简单前馈网络二分类](#1. 简单前馈网络二分类)
- - [1.1 完整代码](#1.1 完整代码)
  - [1.2 代码讲解](#1.2 代码讲解)
  - - [1. 任务与网络结构概述](#1. 任务与网络结构概述)
    - [2. 数据准备](#2. 数据准备)
    - [3. 定义模型（使用 nn.Sequential，最简单方式）](#3. 定义模型（使用 nn.Sequential，最简单方式）)
    - [4. 损失函数与优化器](#4. 损失函数与优化器)
    - [5. 训练循环](#5. 训练循环)
- [2. 简单前馈网络二分类（散点图版）](#2. 简单前馈网络二分类（散点图版）)
- - [2.1 完整代码](#2.1 完整代码)
  - [2.2 代码讲解](#2.2 代码讲解)
  - - [1. 数据准备（生成二维点云）](#1. 数据准备（生成二维点云）)
    - [2. 定义神经网络（SimpleNN 类）](#2. 定义神经网络（SimpleNN 类）)
    - [3. 定义损失函数和优化器](#3. 定义损失函数和优化器)
    - [4. 训练模型（循环迭代）](#4. 训练模型（循环迭代）)
    - [5. 可视化](#5. 可视化)
- 总结

前言

本文通过 PyTorch 实现第一个神经网络，从简单二分类任务入手，逐步展示前馈网络的构建和训练过程。

首先使用虚拟数据演示基本结构，包括数据准备、模型定义、损失函数、优化器和训练循环；其次通过散点图版示例，探索网络在非线性决策边界上的表现，如圆形分类，帮助小白理解网络的灵活性和局限性。

通过代码讲解和可视化，将掌握 PyTorch 的核心流程，为更复杂模型如 CNN 打下基础。

1. 简单前馈网络二分类

我们用 PyTorch 构建一个小型全连接前馈神经网络（Feedforward Neural Network），完成一个二分类任务（输出 0 或 1）。

虽然数据是虚拟的，但代码结构和训练流程与真实项目完全一致。

1.1 完整代码

python 复制代码

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 参数
n_in, n_h, n_out, batch_size = 10, 5, 1, 10

# 数据
x = torch.randn(batch_size, n_in)
y = torch.tensor([[1.0], [0.0], [0.0], [1.0], [1.0], 
                  [1.0], [0.0], [0.0], [1.0], [1.0]])

# 模型
model = nn.Sequential(
    nn.Linear(n_in, n_h),
    nn.ReLU(),
    nn.Linear(n_h, n_out),
    nn.Sigmoid()
)

# 损失 + 优化器
criterion = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

# 训练
losses = []
for epoch in range(50):
    y_pred = model(x)
    loss = criterion(y_pred, y)
    losses.append(loss.item())
    
    print(f'Epoch [{epoch+1}/50], Loss: {loss.item():.4f}')
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

# 可视化1：损失曲线
plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.plot(range(1, 51), losses, 'g-', label='Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss')
plt.grid()

# 可视化2：预测 vs 真实
plt.subplot(1, 2, 2)
y_pred_final = model(x).detach().numpy()
plt.plot(range(1, 11), y.numpy(), 'o-b', label='Actual')
plt.plot(range(1, 11), y_pred_final, 'x--r', label='Predicted')
plt.xlabel('Sample')
plt.ylabel('Value')
plt.title('Actual vs Predicted')
plt.legend()
plt.grid()

plt.tight_layout()
plt.show()

运行结果：

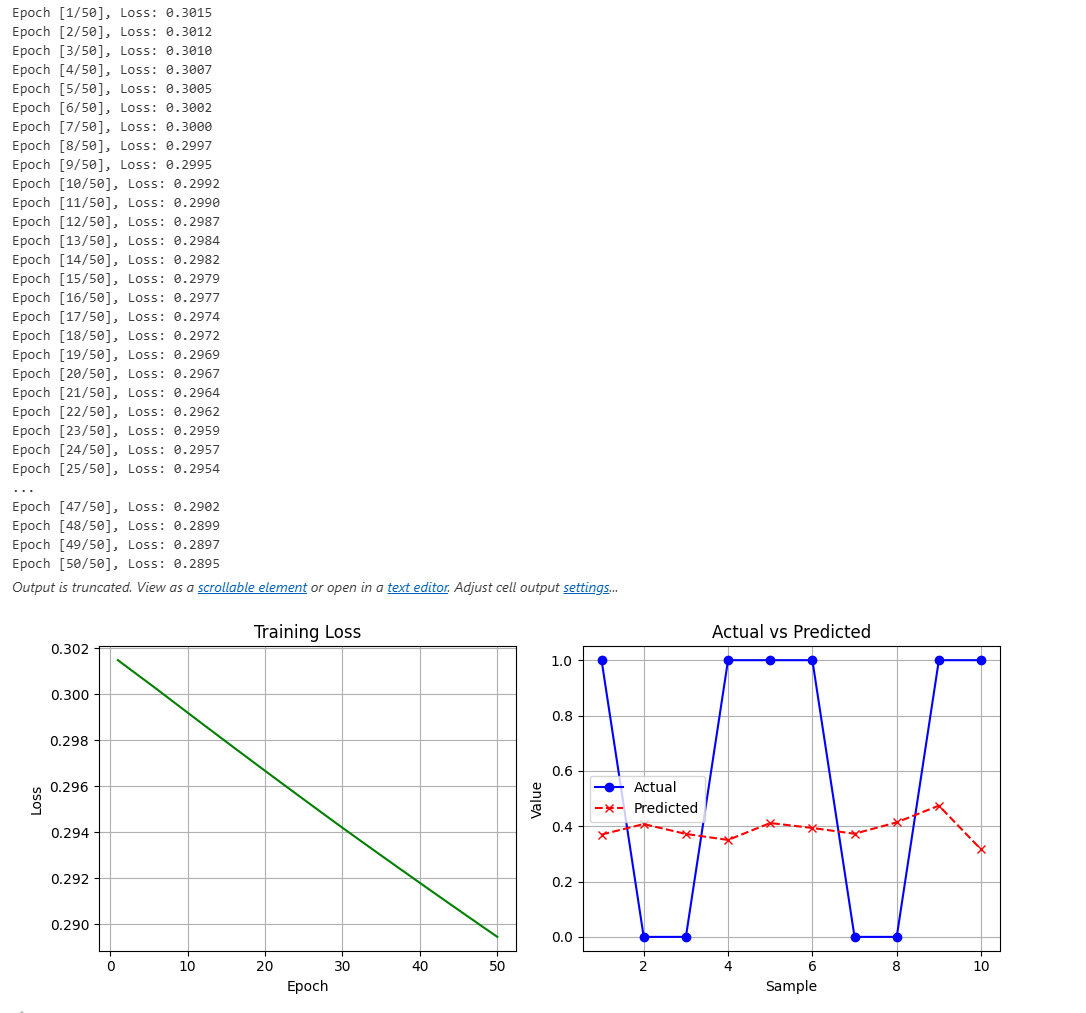
1.2 代码讲解

1. 任务与网络结构概述

任务：二分类（判断样本属于类别 0 还是 1）
网络结构：
- 输入层：10 个特征（n_in = 10）
- 隐藏层：5 个神经元（n_h = 5），使用 ReLU 激活函数（引入非线性）
- 输出层：1 个神经元（n_out = 1），使用 Sigmoid 激活函数（输出概率 0~1）

网络示意图：输入 (10维) → Linear → ReLU → Linear → Sigmoid → 输出 (0~1)
输出层隐藏层输入层特征提取 (5维) Linear: 5 -> 1 Sigmoid 激活 Linear: 10 -> 5 ReLU 激活输入特征: x1...x10 预测概率: y_pred

2. 数据准备

python 复制代码

n_in, n_h, n_out, batch_size = 10, 5, 1, 10

x = torch.randn(batch_size, n_in)  # shape: [10, 10]，随机输入
y = torch.tensor([[1.0], [0.0], [0.0], [1.0], [1.0], 
                  [1.0], [0.0], [0.0], [1.0], [1.0]])  # shape: [10, 1]

x：10 个样本，每个样本 10 个随机特征（正态分布）

y：人为设定的标签（二分类目标），1 表示正类，0 表示负类

3. 定义模型（使用 nn.Sequential，最简单方式）

python 复制代码

model = nn.Sequential(
    nn.Linear(n_in, n_h),   # 第一层线性变换：10 → 5
    nn.ReLU(),              # ReLU 激活：max(0, x)，增加非线性
    nn.Linear(n_h, n_out),  # 第二层线性变换：5 → 1
    nn.Sigmoid()            # Sigmoid：输出压缩到 (0,1)，适合二分类概率
)

在 PyTorch 中，如果你想搭建一个模型，有两种主流方式：一种是像搭积木一样把层排好队的 nn.Sequential，另一种是更灵活但复杂的 nn.Module 类定义。

对于初学者来说，nn.Sequential 是最直观的，因为它就像一个容器，数据按顺序进去，一层层加工，最后出来结果。

虽然它很方便，但它只有一张"单程票"。如果你的网络结构包含以下情况，就不能用它：

多输入/多输出：比如你的模型需要同时输入图片和文字。
残差连接 (Residual Connections)：比如 ResNet 中，数据需要跳过某一层直接传给后面。
分支结构：数据走到一半需要兵分两路处理。

4. 损失函数与优化器

python 复制代码

criterion = nn.MSELoss()                    # 均方误差（回归常用）
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

5. 训练循环

python 复制代码

losses = []  # 记录损失用于画图

for epoch in range(50):
    y_pred = model(x)               # 前向传播
    loss = criterion(y_pred, y)     # 计算损失
    losses.append(loss.item())

    print(f'Epoch [{epoch+1}/50], Loss: {loss.item():.4f}')

    optimizer.zero_grad()           # 清零梯度（必须！）
    loss.backward()                 # 反向传播计算梯度
    optimizer.step()                # 更新所有参数

每轮：前向 → 损失 → 反向 → 更新

损失会逐渐下降（从 ~0.26 降到 ~0.20 左右），说明模型在学习

2. 简单前馈网络二分类（散点图版）

据二维点的位置，判断它在单位圆内（标签1）还是圆外（标签0）。

这是一个非线性决策问题（圆形边界不是直线），普通线性回归办不到，但加隐藏层和激活函数的网络就能学到。

2.1 完整代码

python 复制代码

import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt

# 数据
n_samples = 100
data = torch.randn(n_samples, 2)
labels = (data[:, 0]**2 + data[:, 1]**2 < 1).float().unsqueeze(1)

plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm')
plt.title("Generated Data")
plt.show()

# 模型
class SimpleNN(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(2, 4)
        self.fc2 = nn.Linear(4, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = self.sigmoid(self.fc2(x))
        return x

model = SimpleNN()

# 损失 + 优化
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.1)

# 训练
epochs = 100
for epoch in range(epochs):
    outputs = model(data)
    loss = criterion(outputs, labels)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if (epoch + 1) % 10 == 0:
        print(f'Epoch [{epoch + 1}/{epochs}], Loss: {loss.item():.4f}')

# 可视化边界
def plot_decision_boundary(model, data):
    x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
    y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
    xx, yy = torch.meshgrid(torch.arange(x_min, x_max, 0.1), 
                            torch.arange(y_min, y_max, 0.1), indexing='ij')
    grid = torch.cat([xx.reshape(-1, 1), yy.reshape(-1, 1)], dim=1)
    predictions = model(grid).detach().numpy().reshape(xx.shape)
    plt.contourf(xx, yy, predictions, levels=[0, 0.5, 1], cmap='coolwarm', alpha=0.7)
    plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm', edgecolors='k')
    plt.title("Decision Boundary")
    plt.show()

plot_decision_boundary(model, data)

运行结果：

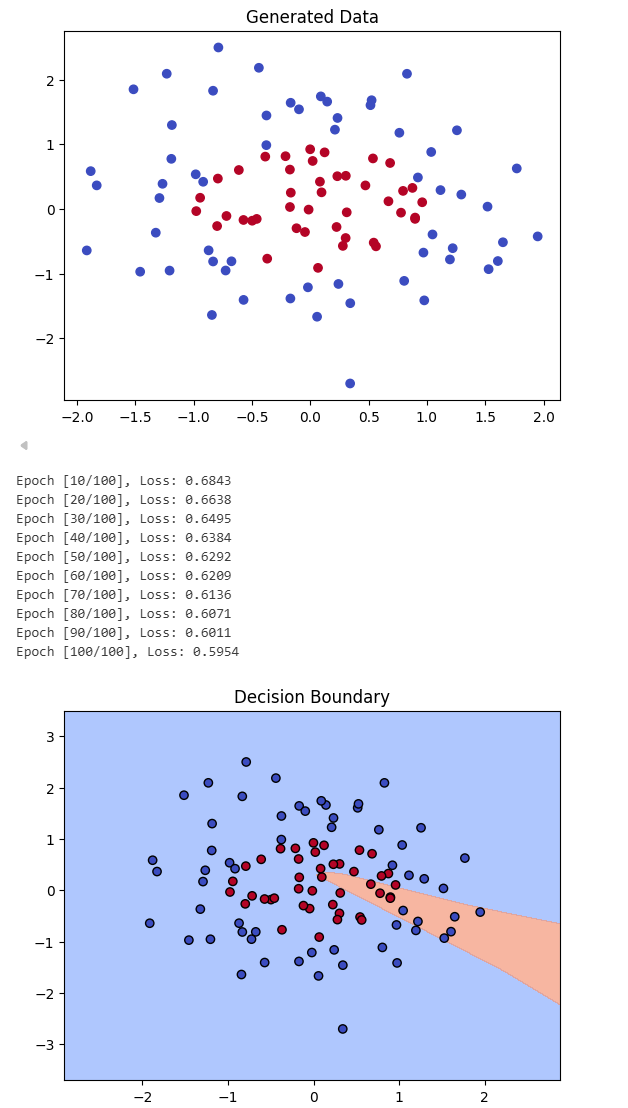
2.2 代码讲解

1. 数据准备（生成二维点云）

python 复制代码

import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt

# 生成随机数据
n_samples = 100
data = torch.randn(n_samples, 2)  # 100 个二维点，服从正态分布
labels = (data[:, 0]**2 + data[:, 1]**2 < 1).float().unsqueeze(1)  # 圆内=1，圆外=0

# 可视化
plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm')
plt.title("Generated Data")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()

解释：

data：形状 [100, 2]，每个行是一个样本（点），两列是特征 x1 和 x2。从 torch.randn 生成，均值0，方差1，模拟随机散点。
labels：形状 [100, 1]。数学公式：如果 x1² + x2² < 1（单位圆内），标签=1（正类）；否则=0。
.float()：转浮点，
.unsqueeze(1)：加维度成列向量（PyTorch 损失函数要求）。
- 为什么这样？创建非线性边界（圆形），测试网络捕捉曲线能力。如果是线性可分（如直线分隔），单层就够；这里需隐藏层。
可视化：scatter 散点图，c=labels 用颜色区分（coolwarm 色图：蓝=0，红=1）。预期：点云围绕原点，圆内红点密集，圆外蓝点。

（上图：类似生成的散点数据，圆内/圆外分类。）

专业知识 ：这是合成数据集，现实中用真实数据（如 Iris）。数学：标签基于欧氏距离，d = √(x1² + x2²) < 1。

这里生成的数据如图所示：

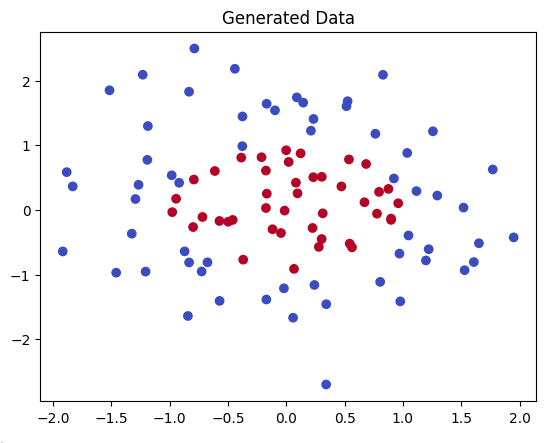
2. 定义神经网络（SimpleNN 类）

python 复制代码

class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        self.fc1 = nn.Linear(2, 4)  # 输入2维 → 隐藏4维
        self.fc2 = nn.Linear(4, 1)  # 隐藏4维 → 输出1维
        self.sigmoid = nn.Sigmoid()  # 输出激活

    def forward(self, x):
        x = torch.relu(self.fc1(x))  # 隐藏层：线性 + ReLU
        x = self.sigmoid(self.fc2(x))  # 输出层：线性 + Sigmoid
        return x

model = SimpleNN()

解释：

继承 nn.Module：PyTorch 所有模型的基类，提供参数管理、GPU 支持等。
init ：定义层。
- fc1：nn.Linear(2,4) 全连接层，权重矩阵 W1 [4,2] + 偏置 b1 [4]。数学：隐藏输出 = W1 * x + b1
- fc2：nn.Linear(4,1)，W2 [1,4] + b2 [1]。输出 = W2 * 隐藏 + b2
- sigmoid：nn.Sigmoid()，公式 σ ( z ) = 1 / ( 1 + e − z ) σ(z) = 1 / (1 + e^{-z}) σ(z)=1/(1+e−z)，输出 [0,1] 概率。
forward：前向传播路径。
- torch.relu：隐藏激活，f(z) = max(0, z)，引入非线性（否则多层还是线性）。
- 为什么隐藏层 4 个神经元？小网络演示；大任务可加层/神经元。

专业知识 ：这是 2-4-1 结构 MLP。参数总数：(24 +4) + (41 +1) = 17。ReLU 避免 Sigmoid 的梯度消失（Sigmoid 导数 max 0.25，易变0）。

3. 定义损失函数和优化器

python 复制代码

criterion = nn.BCELoss()  # 二元交叉熵
optimizer = optim.SGD(model.parameters(), lr=0.1)

解释：

BCELoss：二元交叉熵，适合二分类。公式 L = - [y log(ŷ) + (1-y) log(1-ŷ)]，平均所有样本。
- 为什么 BCE？比 MSE 更好处理概率（预测 0.9 vs 0.1，BCE 惩罚更合理）。
SGD：随机梯度下降，lr=0.1（学习率）。model.parameters() 返回所有权重/偏置。

4. 训练模型（循环迭代）

python 复制代码

epochs = 100
for epoch in range(epochs):
    outputs = model(data)  # 前向
    loss = criterion(outputs, labels)  # 损失

    optimizer.zero_grad()  # 清梯度
    loss.backward()  # 反向
    optimizer.step()  # 更新

    if (epoch + 1) % 10 == 0:
        print(f'Epoch [{epoch + 1}/{epochs}], Loss: {loss.item():.4f}')

解释：

循环：100 轮（epochs），每轮全数据训练（小数据集，无 batch）。
前向：outputs = model(data)，形状 [100,1]，概率值。
损失：criterion 计算 BCE。
反向：zero_grad 清零（梯度累加问题）；backward 计算 ∂L/∂w；step 更新 w -= lr * ∇w。
打印：损失从 ~0.5 降到 ~0.1，模型在学。

5. 可视化

python 复制代码

def plot_decision_boundary(model, data):
    x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
    y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
    xx, yy = torch.meshgrid(torch.arange(x_min, x_max, 0.1), 
                            torch.arange(y_min, y_max, 0.1), indexing='ij')
    grid = torch.cat([xx.reshape(-1, 1), yy.reshape(-1, 1)], dim=1)
    predictions = model(grid).detach().numpy().reshape(xx.shape)
    plt.contourf(xx, yy, predictions, levels=[0, 0.5, 1], cmap='coolwarm', alpha=0.7)
    plt.scatter(data[:, 0], data[:, 1], c=labels.squeeze(), cmap='coolwarm', edgecolors='k')
    plt.title("Decision Boundary")
    plt.show()

plot_decision_boundary(model, data)

解释：

网格生成：xx, yy 创建密集网格点（步长0.1），grid [N,2] 是所有点。
预测：model(grid) 计算每个网格点的概率，reshape 回 2D。
可视化：contourf 填充等高线（>0.5 红区，<0.5 蓝区）；scatter 加原始点。
预期：边界近似圆形，红区内点多为红，蓝区多为蓝。

（上图：类似决策边界，网络学到的圆形分界。）

专业知识：决策边界是 f(x)=0.5 的等值线。detach() 断开梯度，避免内存浪费。

注意：

为什么可视化结果是一条"直线"或"扇形"，而不是圆形边界？

因为 SimpleNN 结构太简单：

self.fc1 = nn.Linear(2, 4)：隐藏层只有 4个神经元。
epochs = 100：只训练了 100轮。

这就是问题所在：

神经元太少：每一个隐藏层的神经元本质上是在空间中画出一道"折痕"。4个神经元最多只能折出 4 条直线。
训练不足 ：从输出日志看，Loss 还在 0.5954。对于二分类，如果模型完全随机猜，Loss 大约是 0.69。0.59 说明模型才刚刚开始摸到一点门道，还没来得及把那 4 条线围成一个圆，只画出了一个"尖角"（如图中那块橙色的区域）。

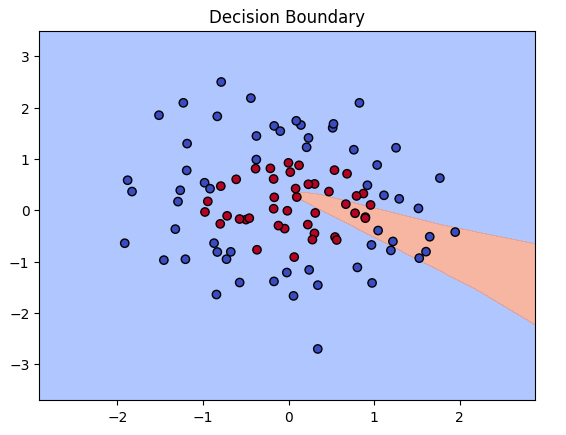
总结

通过两个简单前馈网络二分类示例，可以看到 PyTorch 如何实现模型定义、训练和可视化：从随机数据生成到决策边界绘制，网络通过隐藏层和激活函数捕捉非线性模式，但受限于神经元数量和训练轮次（如在圆形边界任务中可能仅学到近似折线）。

这凸显了神经网络的核心：参数优化依赖梯度下降，性能取决于结构设计和数据质量。掌握这些，已能扩展到真实任务，如图像分类；下一步建议尝试加深层数或用真实数据集实验，继续探索！