4. pytorch线性回归

pytorch线性回归

文章目录

pytorch线性回归
- 前言
- [1. 什么是线性回归](#1. 什么是线性回归)
- [2. pytorch代码实现线性回归](#2. pytorch代码实现线性回归)
- - [2.1 完整代码](#2.1 完整代码)
  - [2.2 代码讲解](#2.2 代码讲解)
  - - [1. 数据准备](#1. 数据准备)
    - [2. 定义线性回归模型](#2. 定义线性回归模型)
    - [3. 定义损失函数 + 优化器](#3. 定义损失函数 + 优化器)
    - [4. 训练循环（核心步骤）](#4. 训练循环（核心步骤）)
    - [5. 评估可视化](#5. 评估可视化)
- 总结

前言

线性回归是深度学习和机器学习的最经典入门算法，虽然简单，却蕴含了现代神经网络的核心思想：通过前向传播计算预测、损失函数衡量误差、反向传播计算梯度、优化器更新参数。

PyTorch 用神经网络的框架实现线性回归，用统一的代码模式（模型、损失、优化器、训练循环）就能轻松扩展到更复杂的深度模型。

1. 什么是线性回归

线性回归是机器学习最基础的算法，用于预测连续数值（如房价、股票）。目标：找到一条"最佳直线"（或超平面）拟合数据。

模型公式： y = w₁x₁ + w₂x₂ + ... + wₙxₙ + b

x：输入特征
w：权重（斜率）
b：偏置（截距）
y：预测值

PyTorch 通过神经网络方式实现它（虽简单，但原理和复杂模型一样）。

训练的本质 ：是通过不断调整 w w w 和 b b b，使得模型输出的 y ^ \hat{y} y^ 与真实值 y y y 之间的距离（即 损失 Loss）达到最小，也就是拟合。

2. pytorch代码实现线性回归

2.1 完整代码

python 复制代码

import torch
import torch.nn as nn
import matplotlib.pyplot as plt

# 设置随机种子，保证结果可复现
torch.manual_seed(42)

# -----------------------------
# 1. 数据准备（生成假数据）
# -----------------------------
X = torch.randn(100, 2)                    # 100 个样本，每个样本 2 个特征
true_w = torch.tensor([2.0, 3.0])          # 真实权重
true_b = 4.0                              # 真实偏置
Y = X @ true_w + true_b + torch.randn(100) * 0.1  # 线性关系 + 噪声

print("前5个样本的特征 X：")
print(X[:5])
print("前5个样本的真实目标 Y：")
print(Y[:5])

# -----------------------------
# 2. 定义线性回归模型
# -----------------------------
class LinearRegressionModel(nn.Module):
    def __init__(self):
        super(LinearRegressionModel, self).__init__()
        self.linear = nn.Linear(2, 1)      # 输入 2 维特征，输出 1 维预测值

    def forward(self, x):
        return self.linear(x)             # 前向传播

model = LinearRegressionModel()

# -----------------------------
# 3. 定义损失函数和优化器
# -----------------------------
criterion = nn.MSELoss()                  # 均方误差损失
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)  # SGD 优化器
# optimizer = torch.optim.Adam(model.parameters(), lr=0.01)  # 也可以用 Adam

# -----------------------------
# 4. 训练模型（新增记录损失）
# -----------------------------
num_epochs = 1000
losses = []  # 用于记录每轮损失，画曲线

for epoch in range(num_epochs):
    model.train()

    # 前向传播
    predictions = model(X)                # shape: [100, 1]
    loss = criterion(predictions.squeeze(), Y)

    # 反向传播与优化
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    losses.append(loss.item())  # 记录损失

    # 每 100 轮打印一次损失
    if (epoch + 1) % 100 == 0:
        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')

# -----------------------------
# 5. 评估模型
# -----------------------------
print('\n训练完成！')
print(f'真实权重: {true_w.numpy()}')
print(f'真实偏置: {true_b}')
print(f'预测权重: {model.linear.weight.data.numpy().squeeze()}')
print(f'预测偏置: {model.linear.bias.data.numpy().squeeze()}')

# 在全部数据上预测
with torch.no_grad():
    predictions = model(X)

# -----------------------------
# 6. 可视化：损失曲线 + 预测结果
# -----------------------------
plt.figure(figsize=(12, 5))

# 子图1：损失曲线
plt.subplot(1, 2, 1)
plt.plot(range(1, num_epochs+1), losses, color='green', linewidth=2)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('训练损失曲线（下降趋势）')
plt.grid(True)

# 子图2：预测 vs 真实值
plt.subplot(1, 2, 2)
plt.scatter(X[:, 0].numpy(), Y.numpy(), color='blue', label='真实值', alpha=0.6)
plt.scatter(X[:, 0].numpy(), predictions.squeeze().numpy(), color='red', label='预测值', alpha=0.6)
plt.xlabel('特征 x1')
plt.ylabel('目标 y')
plt.title('线性回归预测结果')
plt.legend()
plt.grid(True)

plt.tight_layout()
plt.show()

输出：

text 复制代码

前5个样本的特征 X：
tensor([[ 1.9269,  1.4873],
        [ 0.9007, -2.1055],
        [ 0.6784, -1.2345],
        [-0.0431, -1.6047],
        [-0.7521,  1.6487]])
前5个样本的真实目标 Y：
tensor([12.4460, -0.4663,  1.7666, -0.9357,  7.4781])
Epoch [100/1000], Loss: 0.4569
Epoch [200/1000], Loss: 0.0142
Epoch [300/1000], Loss: 0.0082
Epoch [400/1000], Loss: 0.0081
Epoch [500/1000], Loss: 0.0081
Epoch [600/1000], Loss: 0.0081
Epoch [700/1000], Loss: 0.0081
Epoch [800/1000], Loss: 0.0081
Epoch [900/1000], Loss: 0.0081
Epoch [1000/1000], Loss: 0.0081

训练完成！
真实权重: [2. 3.]
真实偏置: 4.0
预测权重: [2.009702  2.9986038]
预测偏置: 4.020907878875732

2.2 代码讲解

1. 数据准备

python 复制代码

import torch
import matplotlib.pyplot as plt

torch.manual_seed(42)  # 固定随机种子，可复现

X = torch.randn(100, 2)               # 100个样本，每个2个特征（正态随机）
true_w = torch.tensor([2.0, 3.0])      # 真实权重（模型要学会这个）
true_b = 4.0                          # 真实偏置
Y = X @ true_w + true_b + torch.randn(100) * 0.1  # y = Xw + b + 噪声

X.shape： [100, 2]
Y.shape： [100]
加噪声模拟真实数据不完美。
输出示例：前5个样本的 X 和对应 Y（如 12.4460 是 1.92692 + 1.48733 + 4 + 噪声）

2. 定义线性回归模型

python 复制代码

import torch.nn as nn

class LinearRegressionModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(2, 1)  # 输入2维，输出1维（自动创建 w 和 b）

    def forward(self, x):
        return self.linear(x)         # y = linear(x)

model = LinearRegressionModel()

nn.Linear(2,1)：内部 weight [1,2]，bias [1]，随机初始化。
forward：定义前向传播（必须实现）。

3. 定义损失函数 + 优化器

python 复制代码

criterion = nn.MSELoss()  # 均方误差：(预测 - 真实)^2 平均

optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
# 或 Adam：optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

MSE：回归任务标准损失。
optimizer：自动更新 model.parameters()（即 w 和 b）。注意这里优化器已经记住了model的参数，后面调用都是直接用optim来更新自己记住的参数。

4. 训练循环（核心步骤）

通过迭代来更新w和b。

python 复制代码

# -----------------------------
# 4. 训练模型（新增记录损失）
# -----------------------------
num_epochs = 1000
losses = []  # 用于记录每轮损失，画曲线

for epoch in range(num_epochs):
    model.train()

    # 前向传播
    predictions = model(X)                # shape: [100, 1]
    loss = criterion(predictions.squeeze(), Y)

    # 反向传播与优化
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    losses.append(loss.item())  # 记录损失

    # 每 100 轮打印一次损失
    if (epoch + 1) % 100 == 0:
        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')

A. 为什么需要 optimizer.zero_grad()？

在 PyTorch 中，梯度是累加的。这意味着如果你不手动清空，这一轮计算出的梯度会直接加到上一轮的梯度上。

如果不清零：梯度会越来越大，导致权重更新失控，模型无法收敛。
为什么要累加？：这在某些高级算法（如梯度累加训练大模型）中很有用，但在基础线性回归中必须清零。

B. loss.backward() 发生了什么？

**当你调用这一行时，PyTorch 会利用自动微分（Autograd）**机制，沿着计算图从 Loss 逆向回推，计算出 Loss 对每个参数（ w w w 和 b b b）的导数：

∂ L o s s ∂ w 和 ∂ L o s s ∂ b \frac{\partial Loss}{\partial w} \quad \text{和} \quad \frac{\partial Loss}{\partial b} ∂w∂Loss和∂b∂Loss

这些导数告诉模型："如果我想让 Loss 变小，权重应该往哪个方向移动？"

C. optimizer.step() 的动作

这行代码执行了最关键的一步：更新参数。根据 SGD 算法，更新公式为：

w n e w = w o l d − learning_rate × gradient w_{new} = w_{old} - \text{learning\_rate} \times \text{gradient} wnew=wold−learning_rate×gradient

减号表示我们沿着梯度的反方向（下降最快的方向）移动。

5. 评估可视化

python 复制代码

# -----------------------------
# 5. 评估模型
# -----------------------------
print('\n训练完成！')
print(f'真实权重: {true_w.numpy()}')
print(f'真实偏置: {true_b}')
print(f'预测权重: {model.linear.weight.data.numpy().squeeze()}')
print(f'预测偏置: {model.linear.bias.data.numpy().squeeze()}')

# 在全部数据上预测
with torch.no_grad():
    predictions = model(X)

# -----------------------------
# 6. 可视化：损失曲线 + 预测结果
# -----------------------------
plt.figure(figsize=(12, 5))

# 子图1：损失曲线
plt.subplot(1, 2, 1)
plt.plot(range(1, num_epochs+1), losses, color='green', linewidth=2)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('训练损失曲线（下降趋势）')
plt.grid(True)

# 子图2：预测 vs 真实值
plt.subplot(1, 2, 2)
plt.scatter(X[:, 0].numpy(), Y.numpy(), color='blue', label='真实值', alpha=0.6)
plt.scatter(X[:, 0].numpy(), predictions.squeeze().numpy(), color='red', label='预测值', alpha=0.6)
plt.xlabel('特征 x1')
plt.ylabel('目标 y')
plt.title('线性回归预测结果')
plt.legend()
plt.grid(True)

plt.tight_layout()
plt.show()

预期：权重 ≈ [2.0, 3.0]，偏置 ≈ 4.0，损失很小。

可视化效果类似这些线性回归拟合图（蓝点真实，红点/线预测，几乎重合）,如图所示。

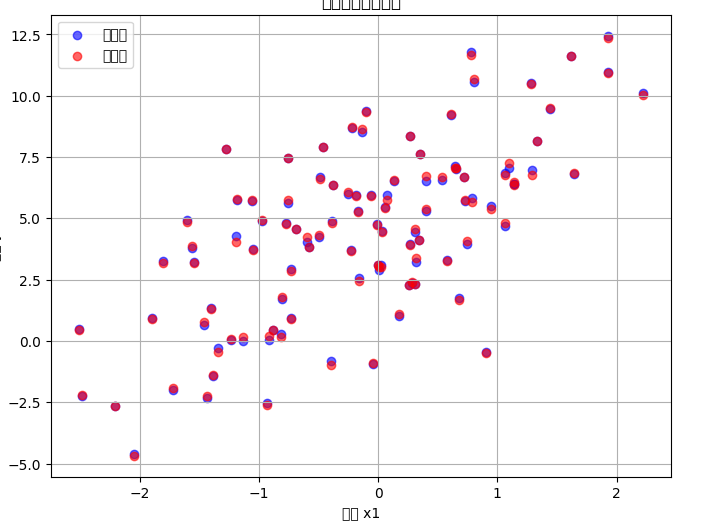
还有损失曲线图：

总结

PyTorch 线性回归的核心流程可概括为**：生成/准备数据 → 定义模型（nn.Linear） → 设置损失（MSE）与优化器（SGD/Adam） → 训练循环（前向 → 损失 → zero_grad → backward → step） → 评估与可视化。**

训练本质是通过梯度下降不断调整权重 w 和偏置 b，使预测值逼近真实值。最终模型参数接近真实设定，损失趋近于 0，预测点与真实点高度重合。