LLM高效微调：Adapt Tuning、Prefix Tuning、LoRA

针对全量微调的昂贵问题，目前主要有两种解决方案：Adapt Tuning和Prefix Tuning，你介绍下

这两个概念问得非常专业！它们是 PEFT（Parameter-Efficient Fine-Tuning，参数高效微调） 领域的两位"开山鼻祖"。

正如你所说，全量微调（Full Fine-Tuning）就像是为了给房子换个壁纸，把整栋楼都拆了重盖，太贵太慢了。我们需要更省钱的办法。

作为老师，我把这两种方法比作**"给大模型做手术的两种不同流派"：一种是 "外挂装备流" (Adapter)，一种是"催眠暗示流" (Prefix)**。

---

1. Adapter Tuning ------ 外挂装备流

这是 2019 年 Google 提出的方案（比 LoRA 还早）。

核心思想：

它不想动大模型原本的身体（冻结原参数），而是选择在大模型的每一层之间，硬塞进去一个小小的"转接头"。

具体做法：

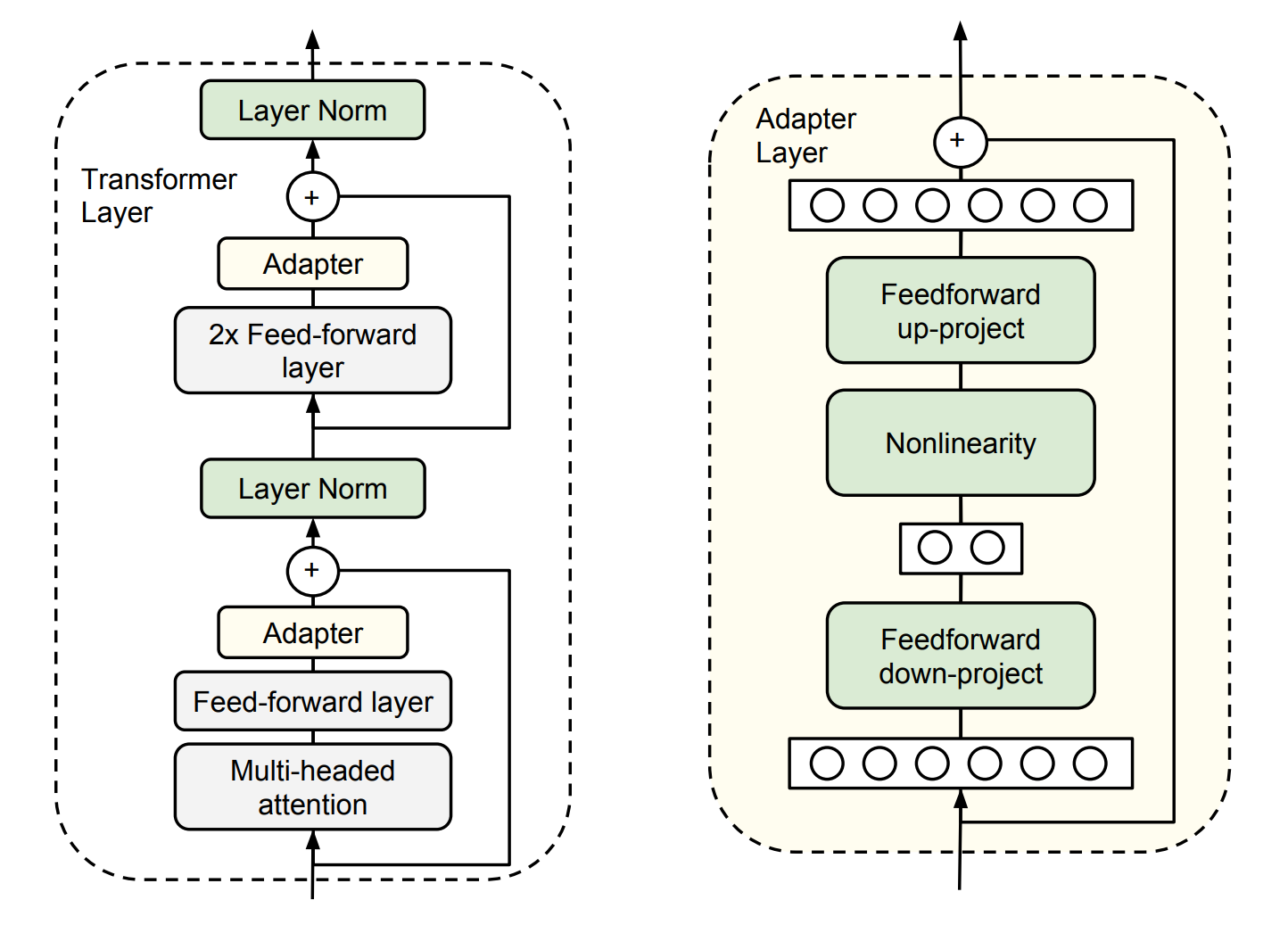
这就好比水管接头。在 Transformer 的每一层（比如 Attention 层或 MLP 层）后面，串联插入两个小的全连接层（MLP）。

这个"转接头"的设计非常巧妙，采用了 Bottleneck（瓶颈）结构：

1. 降维：先把数据的维度从高维（比如 4096）压缩到低维（比如 64）。
2. 激活：过一个非线性激活函数。
3. 升维：再把维度从低维（64）还原回高维（4096）。
4. 残差连接：加上原来的输入，防止把原始信息搞丢了。

为什么叫瓶颈？ 中间那个低维（64）就是瓶颈。因为它很小，所以参数量极少，训练时我们只更新这几个小参数，原来的大模型一动不动。

• 老师的比喻：

  这就像你的电脑（大模型）没有 HDMI 接口，你不想换主板（全量微调），于是你买了一个 USB 转 HDMI 的转接头（Adapter） 插上去。电脑还是那台电脑，但突然拥有了新的功能。

• 缺点：

  虽然训练省参数，但推理（Inference）时，速度会变慢。因为数据流必须要多走过这些新加的层，层数多了，延迟自然就高了。

---

2. Prefix Tuning ------ 催眠暗示流

这是 2021 年斯坦福大学提出的方案。

核心思想：

它不改模型结构，也不加新层，而是在输入的"潜意识"里植入一段虚拟的提示词。

我们知道 Prompt（提示词）通常是人写的文字（比如"请翻译成中文："）。但 Prefix Tuning 认为：为什么提示词非得是人能看懂的文字呢？ 机器只认向量啊。

具体做法：

它在 Transformer 的每一层（不仅仅是输入层），针对 Key (K) 和 Value (V) 矩阵，在前面拼上一段可训练的、连续的向量序列（这就是 Prefix）。

• 这些 Prefix 不是真实的单词（比如不是 "Translate" 这种词的 embedding）。

• 它们是一组纯参数，专门让模型去"领悟"任务的指令。

• 训练时，只训练这些 Prefix 参数，大模型本体冻结。

• 老师的比喻：

  这就像**"盗梦空间"或者"催眠"**。

  • 普通的 Prompt 就像老师在考卷上写："请用莎士比亚风格写作"。
  • Prefix Tuning 就像是直接用脑机接口，把"莎士比亚风格"这个概念植入到模型的潜意识（Key/Value 缓存）里。模型一睁眼（处理输入），脑子里就已经有了这个背景设定，所以它自然而然就会按这个风格说话。

• 优点：

  推理时不需要像 Adapter 那样多算几层，不增加推理延迟（因为 Prefix 可以预先算好存起来）。

• 缺点：

  它占用了上下文窗口（Context Window）。你植入的 Prefix 越长，模型能处理的实际文本长度就越短。而且训练起来有时候不如 Adapter 稳定。

---

老师的总结对比表

特性	Adapter Tuning (外挂装备)	Prefix Tuning (催眠暗示)
形象比喻	加转接头	植入潜意识/小抄
修改位置	在层与层之间插入新模块	在 Attention 的 K/V 前拼接虚拟Token
模型结构	改变了 (层数变多了)	没变 (只是输入变长了)
推理速度	变慢 (多了计算步骤)	不变 (几乎无感)
上下文长度	不影响	变短 (Prefix 占坑位)
当前地位	LoRA 的前身	P-Tuning 的基础

现在的"版本答案"是谁？

你可能会问："老师，那现在大家用哪个？"

其实，现在的王者是 LoRA (Low-Rank Adaptation)。

LoRA 吸收了这两者的精华：

• 像 Adapter 一样是通过旁路矩阵来注入变化，但利用数学技巧（重参数化），在推理时可以将 LoRA 的权重合并到原模型里。
• 结果：推理速度不慢（像 Prefix），也不占上下文（像 Adapter），训练还特别稳。

所以，Adapter 和 Prefix Tuning 是 PEFT 历史上的两座丰碑，理解了它们，你也就理解了为什么 LoRA 会诞生！

Ptuning是什么方法

P-Tuning 是清华大学（唐杰团队）提出的微调方法，它的出现是为了解决**"提示词工程（Prompt Engineering）"**太难搞的问题。

作为老师，我把它称作："AI 的自动翻译官"。

它分为 P-Tuning v1 和 P-Tuning v2 两个版本。理解了它，你就理解了为什么现在很多国产模型（比如 ChatGLM）微调时都推荐用这个。

---

1. 背景：人类的语言 vs 模型的语言

在 P-Tuning 出现之前，如果你想让 GPT-3 做情感分类，你得精心设计提示词：

• 用户A写："Is this review positive or negative?" -> 模型效果 80分
• 用户B写："Classify the sentiment:" -> 模型效果 60分

痛点： 模型太敏感了！差这几个字，效果千差万别。人类很难猜到哪句咒语（Prompt）正好能戳中模型的"爽点"。这种人类能看懂的提示词，叫离散提示（Discrete Prompt）。

---

2. P-Tuning v1：把咒语变成数学向量

P-Tuning v1 的核心思想是：为什么非要用人类的单词做提示词呢？

既然模型内部只认数字（向量），那我们干脆直接训练一组连续的向量 作为提示词，让模型自己去学这组向量该长什么样。这叫连续提示（Continuous/Soft Prompt）。

怎么做的？

它在输入层，把原本的提示词位置（比如 [CLS] Translate this:），替换成了一组可训练的参数 [h0, h1, h2, ...]。

• 人类："请翻译" (固定死的)
• P-Tuning："[向量1, 向量2, 向量3]" (这是可以变形的"液态金属")

关键技巧：LSTM 的引入

P-Tuning v1 发现，如果直接随机初始化这几个向量去训练，效果很差。因为向量之间太独立了，不连贯。

于是作者加了一个 LSTM（或 MLP） 网络来生成这些向量。这就像给这些向量穿了一根线，让它们之间有逻辑关系，训练起来就顺滑多了。

一句话概括 v1： 把"人写的提示词"变成了"机器学的嵌入向量"，只加在输入层。

---

3. P-Tuning v2：向 Prefix Tuning 学习

P-Tuning v1 有个致命弱点 ：它只改了输入层。

对于深层网络（比如 100 层的 LLaMA），输入层的影响力传到后面就微乎其微了。所以 v1 在大规模模型和复杂任务（如文本生成）上效果一般。

P-Tuning v2 吸取了 Prefix Tuning 的经验，做了升级：深层提示（Deep Prompting）。

怎么做的？

它不再只在第一层加提示向量，而是在每一层都加提示向量。

• P-Tuning v1：只在门口放个向导。
• P-Tuning v2：在每一层楼梯口都放个向导，时刻提醒模型该干嘛。

这其实和 Prefix Tuning 非常像了，但 v2 去掉了 Prefix Tuning 中复杂的重参数化（Reparameterization）操作，证明了直接优化每一层的 Prompt 向量也是可行的，而且在小模型（300M）到大模型（100B）上效果都很好。

---

老师的总结对比：三兄弟怎么分？

现在我们把 PEFT 领域的这几个兄弟放一起比一比：

方法	核心操作	插入位置	形象比喻	优缺点
Prefix Tuning	在 Attention 的 K/V 前拼向量	每一层	催眠暗示	效果好，但参数稍微有点难调
P-Tuning v1	把输入 Prompt 换成可训练向量	仅输入层	万能钥匙 (浅层)	适合做分类任务，生成任务表现差
P-Tuning v2	在每一层输入都拼向量	每一层	全程陪跑教练	综合最强，NLU和生成任务通吃

老师的建议：

• 如果你在用 ChatGLM 系列模型，你会发现官方代码库里大量使用 P-Tuning v2。这是因为清华团队对自家算法的针对性优化。
• 但在更广泛的 LLaMA 生态中，LoRA 依然是目前的霸主。

简单记忆：
P-Tuning 就是把"怎么问模型"这件事，也变成了一个可以通过梯度下降来自动学习的参数。

P-Tuning 学习的向量有什么作用，此时还支持用户输入提示词吗

这是一个非常关键的实战问题！作为老师，我可以非常肯定地回答你：

P-Tuning 学习出来的向量绝对支持，且必须支持用户的输入提示词。

为了让你彻底理解它们的关系，我们把 P-Tuning 想象成给大模型装了一个**"万能变声器"**。

---

1. P-Tuning 学习的向量有什么用？（变声器的预设按钮）

这些学习出来的向量（Soft Prompts），本质上是一组**"最优化的任务指令"**。

• 它的作用 ：

  它不是为了给模型提供"知识"，而是为了调整模型的状态，把模型拉入到一个特定的**"任务模式"**中。

• 比喻 ：

  想象你面对一个博学多才但有点精分的专家（大模型）。

  • 没有 P-Tuning：你得自己费劲地描述："请你现在扮演一个翻译官，把下面这句话翻译成英文，不要多嘴......"（这是硬提示，Hard Prompt）。专家可能听得懂，也可能心情不好不理你。
  • 用了 P-Tuning ：你训练了一组向量，这组向量就像是一个**"催眠指令"或"模式开关"**。只要把这组向量往专家脑子（输入层）里一放，专家瞬间眼神一变，自动进入"翻译模式"。他甚至不需要你用语言解释"要翻译"，他的神经元已经被这组向量激活成了翻译专用的状态。

总结：学习到的向量 = 任务特定的"场景设定"或"系统级指令"。

---

2. 此时还支持用户输入提示词吗？（当然！）

不仅支持，而且是必须配合使用。

P-Tuning 的输入结构是这样的：

Input=[Soft Prompts (学习到的向量)]+[Context (用户的输入)] \text{Input} = [\text{Soft Prompts (学习到的向量)}] + [\text{Context (用户的输入)}] Input=[Soft Prompts (学习到的向量)]+[Context (用户的输入)]

或者更形象地表示为：

变声器设置\]+\[你对着麦克风说的话\] \[\\text{变声器设置}\] + \[\\text{你对着麦克风说的话}\] \[变声器设置\]+\[你对着麦克风说的话

实际工作流程是这样的：

1. 准备阶段（P-Tuning 向量） ：

   系统先加载那组训练好的、看不懂的向量（比如长度为 10 的虚拟 Token）。这相当于告诉模型："准备好，接下来我们要进行情感分析了。"

2. 用户输入阶段 ：

   用户输入："这部电影真是太难看了，浪费我时间。"

3. 拼接阶段 ：

   模型实际接收到的序列是：
   [向量1, 向量2, ..., 向量10] + [这部电影真是太难看了，浪费我时间]

4. 推理阶段：

   • 前面的向量引导模型关注"情感"维度。
   • 后面的文字提供具体的分析对象。
   • 模型输出："负面评价"。

---

3. 为什么要这么"混合双打"？

你可能会问："既然 P-Tuning 向量那么厉害，为什么不把用户的输入也训练进去？"

• 学习到的向量（Soft Prompt）：负责**"通用规则"**（Function）。比如"翻译"、"摘要"、"分类"。这些是不变的，需要训练固化下来。
• 用户的输入（User Input）：负责**"具体数据"**（Data）。比如"今天天气不错"、"苹果很好吃"。这是千变万化的，不能被训练死，必须由用户实时输入。

老师的终极图解：

把大模型看作一个**"函数 f(x)"**。

• 传统的微调 ：修改 fff 本身（改模型参数）。
• P-Tuning ：不改 fff，而是给它加一个固定的参数 ppp。
  Result=f(p,x) \text{Result} = f(p, x) Result=f(p,x)
  • ppp (Soft Prompt)：是你训练出来的**"任务参数"**（比如 ppp 代表"翻译模式"）。
  • xxx (User Input)：是用户填写的**"变量"**。

所以，P-Tuning 的本质就是通过训练找到那个最完美的参数 ppp，让函数 fff 在处理任何用户输入 xxx 时，都能表现得最好。

什么是LoRA 微调

这是一个非常棒的压轴问题！LoRA (Low-Rank Adaptation) 是目前微调领域绝对的**"顶流"和"版本答案"**。

如果你现在的显存不够大（比如只有一张家用 3090/4090 显卡），想训练一个像 LLaMA 3 这样的大模型，LoRA 是你唯一的救星。

作为老师，我把 LoRA 称为："给大模型贴便利贴的大师"。

---

1. 为什么需要 LoRA？（核心痛点）

我们回顾一下之前讲过的：

• 全量微调：太贵。改动 7B 模型的参数，需要极大的显存来存梯度和优化器状态。
• Adapter：虽然省参数，但推理变慢（加了层）。
• Prefix/P-Tuning：虽然省参数，但占用了提示词长度，效果有时候不太稳。

LoRA 的出现，就是为了既省显存，又不让推理变慢，效果还要好。

---

2. LoRA 的核心原理：矩阵分解的魔法

LoRA 的全称是 Low-Rank Adaptation（低秩自适应）。

(1) 直观比喻：便利贴模式

想象一本超级厚的百科全书（大模型权重 WWW），里面的知识是固定的。

现在你要让这本书学会"说东北话"。

• 全量微调：把整本书重新印刷一遍，把里面的字句全改了。工程量巨大。

• LoRA ：

  我们不改书的内容。我们在书的旁边，挂一个小本子（旁路矩阵）。

  在这个小本子上记录："遇到'你好'，请读作'老铁'"。

  推理的时候：最终输出 = 原书内容 + 小本子上的修正值。

(2) 数学原理：拆解大胖子

大模型的一个权重矩阵 WWW 通常非常大，比如 1000×10001000 \times 10001000×1000（这就 100 万个参数了）。

如果要微调它，通常我们要算一个更新量 ΔW\Delta WΔW。

微软的研究员发现：虽然模型参数很多，但真正起作用的"变化量"其实并不需要那么高的维度（Low Rank）。

于是，LoRA 用两个极小的矩阵 (AAA 和 BBB) 相乘 来模拟这个巨大的变化量 ΔW\Delta WΔW。

Wnew=Wold+B×A⏟ΔW W_{new} = W_{old} + \underbrace{B \times A}_{\Delta W} Wnew=Wold+ΔW B×A

• WoldW_{old}Wold ：原始大模型权重（比如 1000×10001000 \times 10001000×1000）。冻结不动！
• BBB ：降维矩阵（比如 1000×81000 \times 81000×8）。可训练！
• AAA ：升维矩阵（比如 8×10008 \times 10008×1000）。可训练！

算一算账：

• 原来要训练：1000×1000=1,000,0001000 \times 1000 = 1,000,0001000×1000=1,000,000 个参数。
• 现在只要训练：(1000×8)+(8×1000)=16,000(1000 \times 8) + (8 \times 1000) = 16,000(1000×8)+(8×1000)=16,000 个参数。

结论： 训练参数量直接缩小了 60 多倍 ！而且那个 888 叫做 Rank (秩)，是一个超参数，通常设为 8, 16, 64 就足够了。

---

3. LoRA 的"杀手锏"：零推理延迟 (Zero Inference Latency)

这是 LoRA 打败 Adapter 的关键。

• Adapter 是在层之间串联新层，数据流必须多走几步，所以慢。
• LoRA 是在旁边搞"旁路"。

但在**推理（部署）**的时候，我们可以运用小学数学的分配律：

x⋅Wnew=x⋅(Wold+B⋅A)=x⋅Wold+x⋅(B⋅A) x \cdot W_{new} = x \cdot (W_{old} + B \cdot A) = x \cdot W_{old} + x \cdot (B \cdot A) x⋅Wnew=x⋅(Wold+B⋅A)=x⋅Wold+x⋅(B⋅A)

因为 WoldW_{old}Wold、BBB、AAA 都是矩阵，我们可以直接把 B×AB \times AB×A 算出来，加回到 WoldW_{old}Wold 里去！

Wmerged=Wold+(B×A) W_{merged} = W_{old} + (B \times A) Wmerged=Wold+(B×A)

这意味着什么？

训练完后，我们可以把那张"便利贴"**彻底融合（Merge）**进大模型里。

融合后的模型，结构和原来一模一样 ，没有任何多余的层。

所以，它的推理速度和原版模型完全一致，没有任何变慢！

---

4. 老师的总结图表

特性	全量微调 (Full FT)	Adapter / Prefix	LoRA
训练参数量	100% (巨大)	<1% (很小)	<1% (很小)
显存需求	极高 (需多卡A100)	低 (单卡可跑)	低 (单卡可跑)
推理延迟	无延迟	有延迟 (变慢)	无延迟 (可合并权重)
存储空间	几十 GB	几 MB	几 MB
多任务切换	难 (需存多个大模型)	易	极易 (换挂件即可)

5. 什么时候用 LoRA？

答案是：现在几乎所有时候。

• 你想把自己公司的文档喂给 LLaMA，让它当客服 -> 用 LoRA。
• 你想让 Stable Diffusion 生成特定画风（比如宫崎骏风格）的图 -> 用 LoRA（SD 社区里 LoRA 也是主流）。
• 你只有一张 24G 显存的卡，想微调 7B 的模型 -> 必须用 LoRA（配合 QLoRA 量化技术效果更佳）。

一句话总结：
LoRA 就是通过"四两拨千斤"的数学技巧，用极小的参数代价，实现了近似全量微调的效果，而且事后还能完美融合，不留痕迹。

为什么LoRA训练，开始对 A 使用随机高斯初始化，对 B 使用零初始化

这是一个非常硬核且具有洞察力的问题！这触及到了深度学习中**初始化（Initialization）**的核心哲学。

作为老师，我可以用一句话先告诉你答案：
为了让训练开始的第一刻，LoRA 就像不存在一样（ΔW=0\Delta W = 0ΔW=0），同时又保证梯度能够流动起来。

让我们像剥洋葱一样，从**"为什么要 0"和"为什么不能全是 0"**两个角度来拆解。

---

1. 核心目标：先别捣乱（Keep Silent）

LoRA 的公式是：
Wnew=Wold+ΔW=Wold+(B×A) W_{new} = W_{old} + \Delta W = W_{old} + (B \times A) Wnew=Wold+ΔW=Wold+(B×A)

• WoldW_{old}Wold：预训练好的大模型参数，它是经过几万亿 token 训练出来的"智慧结晶"。
• B×AB \times AB×A：LoRA 这个"实习生"提出的修改意见。

在训练还没开始的时候（Step 0）：

我们希望这个"实习生"最好闭嘴，先乖乖听"老专家"(WoldW_{old}Wold) 的话。

如果一开始 B×AB \times AB×A 就产生了一个非零的随机矩阵，那就相当于在原模型的权重上加了一层随机噪声。

• 后果：模型的预测能力瞬间崩塌，Loss 会瞬间飙升，模型还没开始学新东西，先得花时间去抵消这股随机噪声的影响。
• 解决 ：必须保证初始状态下 B×A=0B \times A = 0B×A=0。

为了让乘积为 0，AAA 和 BBB 里至少得有一个是全 0 矩阵。

---

2. 进阶问题：为什么不两个都设为 0？

既然要结果为 0，那把 AAA 和 BBB 都初始化为 0 岂不是更稳？

不行！这就涉及到"梯度消失"和"对称性打破"的问题了。

我们需要看一看**反向传播（Backpropagation）**时梯度是怎么算的。

假设 Loss 为 LLL，对于 BBB 的梯度计算大概是这样（简化版）：

∂L∂B=∂L∂(B×A)⋅AT \frac{\partial L}{\partial B} = \frac{\partial L}{\partial (B \times A)} \cdot A^T ∂B∂L=∂(B×A)∂L⋅AT

注意看公式最后那个 ATA^TAT。

• 如果 AAA 也是 0 ：
  那么 ∂L∂B\frac{\partial L}{\partial B}∂B∂L 算出来直接就是 0。
• 如果 BBB 是 0 （同理）：
  ∂L∂A\frac{\partial L}{\partial A}∂A∂L 也要依赖 BBB，如果 BBB 一开始也是 0，那么 AAA 的梯度也是 0。

结论 ：如果 AAA 和 BBB 都是 0，由于它们互相依赖对方来计算梯度，它们两个就都收不到更新信号，永远卡在 0 这个位置动不了（或者变成完全对称的更新，极难收敛）。这就像两个死锁的齿轮。

---

3. 完美策略：一个 0，一个随机

为了解开这个死锁，LoRA 采取了**"混合初始化"**策略：

• AAA (降维矩阵) ：使用 高斯分布 (Random Gaussian) 初始化。
  • 潜台词：我有数值，我有能量，但我暂时还没被放大。
• BBB (升维矩阵) ：使用 全 0 (Zeros) 初始化。
  • 潜台词：我把阀门关死了。

这时候发生的神奇反应：

1. 前向传播 (Forward) ：
   ΔW=B(全0)×A(有数)=0 \Delta W = B(\text{全0}) \times A(\text{有数}) = 0 ΔW=B(全0)×A(有数)=0

   • 效果 ：完美！模型输出完全等于 WoldW_{old}Wold，没有任何噪声干扰。

2. 反向传播 (Backward) ：

   我们来看 BBB 的梯度：
   GradientB∝Error×A \text{Gradient}_B \propto \text{Error} \times A GradientB∝Error×A

   • 因为 AAA 不是 0 （它是高斯随机数），所以 BBB 能收到有效的梯度！
   • 于是，在第一次更新后，BBB 就不再是 0 了。

3. 后续迭代 ：

   一旦 BBB 变成了非 0，AAA 在下一次计算梯度时（依赖 BBB），也能收到梯度了。
   齿轮转动起来了！

---

老师的形象比喻

把 LoRA 想象成一个吉他放大器的音量旋钮。

• AAA (高斯初始化) ：就像是吉他的琴弦。它必须处于"振动"状态（有随机值），准备好发出声音。
• BBB (零初始化) ：就像是总音量旋钮 。
  • 一开始，我们需要把音量旋钮拧到 0 （B=0B=0B=0）。
  • 为什么？ 因为我们要保证刚开机时，不会突然发出巨大的噪音吓到人（保证模型初始表现正常）。
  • 为什么琴弦不能静止？ 如果琴弦不动（A=0A=0A=0），那你怎么拧音量旋钮（更新 BBB），音箱里都没声音，你也根本不知道该往哪边拧（没有梯度）。

所以：琴弦要震动（A随机），音量要归零（B为零）。 这样既安静，又能随时开始演奏。

LoRA中文叫什么。怎么从数学角度全面理解

这也是一个非常标准且必要的提问。作为老师，我很高兴你能从"怎么用"进阶到想探究"数学本质"。

1. 中文名称

LoRA (Low-Rank Adaptation) 的中文名称通常翻译为：

"低秩自适应"

也有人称为"低秩适配微调"。

---

2. 数学角度全面理解：从"本征维度"到"矩阵分解"

要从数学上彻底理解 LoRA，我们需要拆解为 4 个核心数学概念：本征维度假设 、矩阵分解 、缩放因子 、以及线性性质。

第一层：理论基石------本征维度假设 (Intrinsic Dimension)

这是 LoRA 成立的根本原因。

• 背景 ：一个全量微调的模型，它的参数更新量记为 ΔW\Delta WΔW。假设模型维度是 d×dd \times dd×d（比如 4096×40964096 \times 40964096×4096），那么 ΔW\Delta WΔW 也是一个 4096×40964096 \times 40964096×4096 的大矩阵，包含 1600 万个参数。

• 假设 ：微软的研究人员基于先前的研究（Aghajanyan et al., 2020）提出，虽然 ΔW\Delta WΔW 看起来很大，但它其实是"虚胖"的。
  "模型在特定任务上的改变，其实只需要极少的参数就能描述清楚。"

  这就是所谓的**"低秩（Low-Rank）"**属性。

• 数学表达 ：

  虽然 ΔW∈Rd×d\Delta W \in \mathbb{R}^{d \times d}ΔW∈Rd×d，但它的秩 (Rank) 其实非常低。也就是说，存在一个 r≪dr \ll dr≪d（rrr 远小于 ddd），使得我们可以完美（或近似完美）地重构这个更新量。

  老师的比喻 ：

  就像一个三维物体（高维数据）投射在墙上的影子（低维数据）。虽然物体在动，但如果我们只关心影子的变化，其实不需要记录三维坐标，二维坐标就够了。

第二层：核心操作------低秩矩阵分解 (Matrix Decomposition)

基于上面的假设，既然 ΔW\Delta WΔW 是低秩的，那我们为什么要傻傻地存一个 d×dd \times dd×d 的大矩阵呢？

我们用两个极小的矩阵相乘来表示它：

ΔW=B⋅A \Delta W = B \cdot A ΔW=B⋅A

• 维度设定：

  • ΔW\Delta WΔW: d×kd \times kd×k (原始维度)
  • BBB: d×rd \times rd×r (高瘦矩阵)
  • AAA: r×kr \times kr×k (矮胖矩阵)
  • rrr: Rank (秩)，LoRA 的核心超参数。通常取 8, 16, 32。

• 参数量对比（数学账） ：

  假设 d=4096,k=4096,r=8d=4096, k=4096, r=8d=4096,k=4096,r=8。

  • 全量微调 (ΔW\Delta WΔW) ：4096×4096≈4096 \times 4096 \approx4096×4096≈ 16,770,000 个参数。
  • LoRA (A+BA+BA+B) ：4096×8+8×4096=32,768×2≈4096 \times 8 + 8 \times 4096 = 32,768 \times 2 \approx4096×8+8×4096=32,768×2≈ 65,000 个参数。
  • 压缩率 ：6.5万/1677万≈0.3%6.5万 / 1677万 \approx 0.3\%6.5万/1677万≈0.3%。省了 99.7% 的参数！

第三层：控制旋钮------缩放因子 (Scaling Factor) α\alphaα

很多同学只知道 rrr，但忽略了公式里还有一个隐藏的 α\alphaα。

LoRA 的完整前向传播公式其实是这样的：

h=W0x+αr(BAx) h = W_0 x + \frac{\alpha}{r} (BAx) h=W0x+rα(BAx)

• α\alphaα (Alpha) ：这也是一个超参数，通常设为和 rrr 一样大，或者 2r2r2r。
• rrr (Rank)：矩阵的秩。
• αr\frac{\alpha}{r}rα 的数学意义 ：
  它起到了一个**"恒定放大器"**的作用。
  • 当我们调整 rrr 的大小时（比如从 8 改成 16），矩阵 AAA 和 BBB 的数值分布特性会发生变化。
  • 如果没有这个 αr\frac{\alpha}{r}rα，每次改 rrr，我们都得重新去调学习率（Learning Rate）。
  • 加上这个系数后，相当于把 A×BA \times BA×B 的输出幅度归一化了。无论你怎么改 rrr，都不用大幅调整学习率。

第四层：终极奥义------线性的分配律 (Distributive Property)

为什么 LoRA 推理不慢？因为矩阵乘法满足分配律。

推理时的公式推导：

Output=Input×Wfinal=x⋅(Wold+ΔW)=x⋅Wold+x⋅(B⋅A)⋅αr \begin{aligned} Output &= \text{Input} \times W_{final} \\ &= x \cdot (W_{old} + \Delta W) \\ &= x \cdot W_{old} + x \cdot (B \cdot A) \cdot \frac{\alpha}{r} \end{aligned} Output=Input×Wfinal=x⋅(Wold+ΔW)=x⋅Wold+x⋅(B⋅A)⋅rα

虽然训练时我们是分开算的（xxx 走两路，一路走 WoldW_{old}Wold，一路走 BABABA）。

但在部署（Inference）时，我们可以提前算出：

Wmerged=Wold+αr(B⋅A) W_{merged} = W_{old} + \frac{\alpha}{r} (B \cdot A) Wmerged=Wold+rα(B⋅A)

因为 WoldW_{old}Wold 和 B⋅AB \cdot AB⋅A 都是 d×kd \times kd×k 的矩阵，它们可以直接相加 。

加完之后，模型就变回了原来的样子，没有任何额外的计算分支。

---

3. 老师的"数学直觉"总结图

为了帮你彻底记住，我们建立一个**"原本 vs 增量"**的数学直觉：

1. 目标 ：寻找 Y=(W+ΔW)XY = (W + \Delta W)XY=(W+ΔW)X
2. 全量微调 ：直接暴力求解 ΔW\Delta WΔW 的所有元素。
3. LoRA ：认为 ΔW\Delta WΔW 是贫瘠的（Sparse/Low-Rank），大部分信息是冗余的。
   • 于是假设 ΔW\Delta WΔW 可以被压缩为两个小向量空间的映射。
   • AAA：将高维特征空间 降维 到低维流形（Manifold）。
   • BBB：将低维流形的信息 升维 还原回高维空间。
4. 初始化 ：
   • A∼N(0,σ2)A \sim \mathcal{N}(0, \sigma^2)A∼N(0,σ2) (高斯分布)：保证低维空间里有初始的随机扰动方向。
   • B=0B = 0B=0 (全零)：保证初始时刻没有任何扰动传回高维空间 (ΔW=0\Delta W=0ΔW=0)，让模型从预训练状态平滑起步。

这就是 LoRA 从数学定义到初始化策略的完整闭环逻辑。

Alpha和Rank一样大，Alpha/Rank不就是1了吗，有什么意义

这是一个非常敏锐的直觉！很多初学者（甚至有经验的炼丹师）都会在这里产生疑惑。

如果 α\alphaα 和 rrr 一样大，那 αr=1\frac{\alpha}{r} = 1rα=1，这公式写着确实像个"脱裤子放屁"的多余操作。

但作为老师，我要告诉你：在实际炼丹中，α\alphaα 和 rrr 通常是不一样的，而且这个设计是为了让你在调参时"少掉几根头发"。

主要有以下三个核心意义：

---

1. 核心作用：解耦"学习率"与"秩" (Decoupling)

这是 LoRA 原论文作者设计这个系数的根本原因。

假设你正在做一个实验，你想看看 rrr（模型的复杂程度）对效果的影响。

你先试了 r=8r=8r=8，把学习率 (Learning Rate, LR) 调到了 1e−41e^{-4}1e−4，效果不错。

接着，你想试试 r=128r=128r=128。

• 如果没有 αr\frac{\alpha}{r}rα ：

  因为 rrr 变大了，矩阵 AAA 和 BBB 的维度变大了，做矩阵乘法 (B×AB \times AB×A) 时，求和项变多了 。这会导致输出的数值幅度（Magnitude）和梯度（Gradient）都变大。

  这时候，之前的学习率 1e−41e^{-4}1e−4 可能就太大了，模型会梯度爆炸。你被迫必须重新去调学习率，比如调到 1e−51e^{-5}1e−5。这非常麻烦！

• 有了 αr\frac{\alpha}{r}rα ：

  当 rrr 变大时（比如扩大了 16 倍），分母上的 rrr 也会变大。
  分子的矩阵乘法变大了，分母的 rrr 也变大了，两者刚好抵消。

结论： 这个缩放因子保证了，无论你怎么改变 rrr，你都不需要重新去调学习率。 它自动帮你把梯度的尺度归一化了。

---

2. 实际用法：α\alphaα 通常固定，只调 rrr

在工业界实战（比如使用 HuggingFace 的 peft 库）中，大家通常的习惯是：

把 α\alphaα 焊死在一个数值上（比如 16 或 32），然后去调整 rrr。

我们来看个例子：

设定 α=32\alpha = 32α=32（固定不变）。

• 实验 A (r=8r=8r=8) ：缩放因子 = 32/8=432/8 = \mathbf{4}32/8=4。
  • 含义：因为 rrr 很小，模型能力弱，我们给它放大 4 倍的权重，让它学得快点。
• 实验 B (r=64r=64r=64) ：缩放因子 = 32/64=0.532/64 = \mathbf{0.5}32/64=0.5。
  • 含义：因为 rrr 很大，参数很多，求和累积效应强，我们给它缩小 0.5 倍，防止它学过头或震荡。

你看，这时候 αr\frac{\alpha}{r}rα 就不等于 1 了！ 它变成了一个**"自动平衡器"**。

---

3. 另一种视角：α\alphaα 就是 LoRA 专属的学习率

我们可以从数学上把公式重写一下。

假设优化器的全局学习率是 η\etaη (Learning Rate)。

模型更新的本质步伐是：
Step=η×αr×∇(Gradient) \text{Step} = \eta \times \frac{\alpha}{r} \times \nabla (Gradient) Step=η×rα×∇(Gradient)

这里 η×αr\eta \times \frac{\alpha}{r}η×rα 其实可以看作是 LoRA 层的"等效学习率"。

• η\etaη (LR)：控制所有层的步伐。
• α\alphaα (Alpha)：专门控制 LoRA 这一层的步伐幅度。

为什么这很有意义？

有时候我们微调大模型，会采用分层学习率。比如：

• 原模型的 LayerNorm 层我们想微调一下，用很小的 LR。
• LoRA 层我们想让它剧烈变化，用很大的 LR。

通过调整 α\alphaα（比如把 α\alphaα 设得很大），我们就可以在不改变全局 LR 的情况下，单独放大 LoRA 层的更新幅度。

---

老师的总结

1. 当 α=r\alpha = rα=r 时：你说得对，数学上它就是 1，确实没意义。但在代码实现里，这是一种"默认的安全配置"。
2. 当 α\alphaα 固定时 ：它是为了抵消 rrr 变化带来的梯度波动 ，让你换 rrr 的时候不用重新调参。
3. 从调参角度 ：α\alphaα 是 LoRA 模块的**"音量旋钮"**。rrr 决定音质的丰富度，α\alphaα 决定声音的大小。

实战建议：

如果你在炼丹，通常建议设置 α=2×r\alpha = 2 \times rα=2×r 或者直接固定 α=32\alpha=32α=32，这样效果通常比较稳。不要纠结于让它们相等。