PyTorch优化器完全指南

Niuguangshuo2025-12-24 10:15

引言：优化器的作用

在深度学习中，优化器是驱动模型学习的"引擎" 。想象你在一座高山上寻找最低点（全局最小点），梯度告诉你下山的方向，而优化器则决定了你下山的策略------是小心谨慎地一小步一小步走，还是大胆地跳跃前进？

要理解优化器的完整作用，需要了解深度学习中几个核心概念的相互关系：

python 复制代码 
# 一个完整的训练循环，展示优化器在整个训练流程中的位置
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

for epoch in range(num_epochs):
    optimizer.zero_grad()      # 1. 清空之前的梯度
    outputs = model(inputs)    # 2. 前向传播
    loss = criterion(outputs, targets)  # 3. 计算损失
    loss.backward()            # 4. 反向传播计算梯度
    optimizer.step()           # 5. 优化器更新参数

深度学习训练流程回顾：

  1. 损失函数：衡量模型预测值与真实值之间的差异
  2. 梯度：损失函数相对于模型参数的导数，指示参数更新方向
  3. 反向传播：计算梯度的高效算法
  4. 模型权重更新：根据梯度和学习策略调整模型参数
  5. 优化器：实现权重更新的算法

关于这些概念的详细解释和相互关系，可以参考我之前写的博客：深度学习：损失函数、梯度、反向传播、模型权重更新与优化器的关系

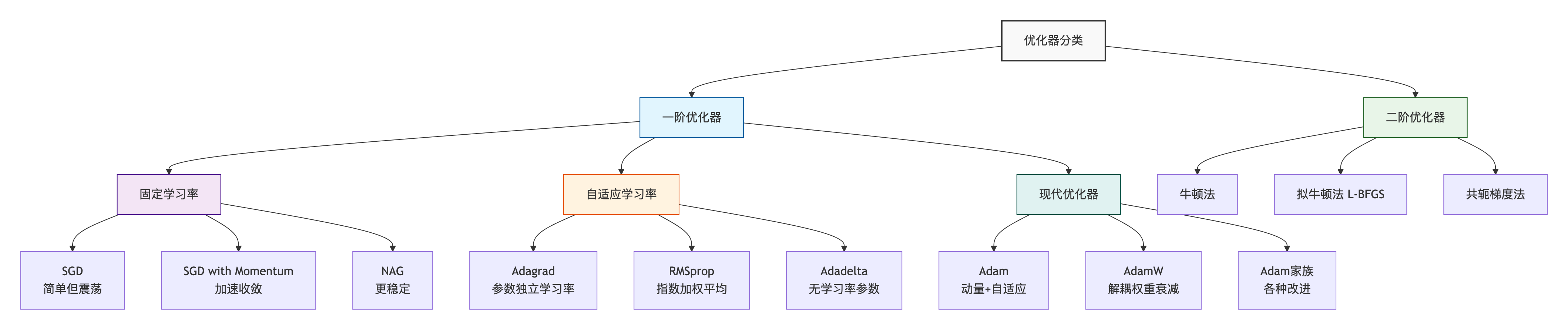
一、基础优化器

1. 随机梯度下降（SGD）

数学公式 ：
θ t + 1 = θ t − η ⋅ g t \theta_{t+1} = \theta_t - \eta \cdot g_t θt+1=θt−η⋅gt

参数说明：

  • θ t \theta_t θt：第t次迭代时的模型参数
  • η \eta η：学习率（learning rate），控制参数更新的步长
  • g t = ∇ θ L ( θ t ) g_t = \nabla_{\theta} L(\theta_t) gt=∇θL(θt)：损失函数在 θ t \theta_t θt处的梯度

PyTorch实现：

python 复制代码 
import torch.optim as optim

# 初始化SGD优化器
optimizer_sgd = optim.SGD(
    model.parameters(),
    lr=0.01,          # 学习率
    momentum=0.9,     # 动量系数（用于SGDM和NAG）
    nesterov=True,    # 启用Nesterov动量（用于NAG）
    weight_decay=1e-4  # 权重衰减（L2正则化）
)

"""
参数说明：
- params: 要优化的参数，通常是model.parameters()
- lr: 学习率，控制每次更新的步长
- momentum: 动量系数
  - 0表示使用基础SGD
  - >0表示使用SGDM（SGD with Momentum）
- nesterov: 是否启用Nesterov动量
  - False表示使用SGDM
  - True表示使用NAG（Nesterov Accelerated Gradient）
- weight_decay: 权重衰减系数（L2正则化），用于防止过拟合
"""

2. SGD with Momentum - 加入动量

数学公式 ：

动量法模拟了物理中的动量概念，帮助优化器"冲"过局部最小值：

v t = γ v t − 1 + η ⋅ g t θ t + 1 = θ t − v t \begin{aligned} v_t &= \gamma v_{t-1} + \eta \cdot g_t \\ \theta_{t+1} &= \theta_t - v_t \end{aligned} vtθt+1=γvt−1+η⋅gt=θt−vt

参数说明：

  • v t v_t vt：第t次迭代的速度（动量项）
  • γ \gamma γ：动量系数，通常设为0.9
  • η \eta η：学习率
  • g t g_t gt：损失函数在 θ t \theta_t θt处的梯度
  • θ t \theta_t θt：第t次迭代时的模型参数
  • 当梯度方向一致时，动量会累积，加速收敛；当梯度方向变化时，动量能减少震荡

PyTorch实现 ：同SGD优化器，设置momentum参数大于0

3. Nesterov Accelerated Gradient (NAG)

数学公式 ：

NAG 是动量法的改进，先根据动量方向"看"一步，再计算梯度：

v t = γ v t − 1 + η ⋅ ∇ θ L ( θ t − γ v t − 1 ) θ t + 1 = θ t − v t \begin{aligned} v_t &= \gamma v_{t-1} + \eta \cdot \nabla_{\theta} L(\theta_t - \gamma v_{t-1}) \\ \theta_{t+1} &= \theta_t - v_t \end{aligned} vtθt+1=γvt−1+η⋅∇θL(θt−γvt−1)=θt−vt

参数说明：

  • v t v_t vt：第 t t t次迭代的速度（动量项）
  • γ \gamma γ：动量系数，通常设为 0.9，控制动量的影响程度
  • η \eta η：学习率，控制每次更新的步长
  • ∇ θ L ( θ t − γ v t − 1 ) \nabla_{\theta} L(\theta_t - \gamma v_{t-1}) ∇θL(θt−γvt−1)：在调整后的参数位置计算的梯度
  • θ t \theta_t θt：第 t t t次迭代时的模型参数

PyTorch实现 ：同SGD优化器，设置momentum大于0且nesterov=True

二、自适应学习率优化器

1. Adagrad - 自适应梯度

数学公式 ：

Adagrad为每个参数设置不同的学习率，频繁更新的参数学习率小：

G t = G t − 1 + g t 2 θ t + 1 = θ t − η G t + ϵ ⋅ g t \begin{aligned} G_t &= G_{t-1} + g_t^2 \\ \theta_{t+1} &= \theta_t - \frac{\eta}{\sqrt{G_t + \epsilon}} \cdot g_t \end{aligned} Gtθt+1=Gt−1+gt2=θt−Gt+ϵ η⋅gt

参数说明：

  • G t G_t Gt：到第t次迭代为止，梯度平方的累积和
  • θ t \theta_t θt：第t次迭代时的模型参数
  • η \eta η：学习率
  • g t g_t gt：损失函数在 θ t \theta_t θt处的梯度
  • ϵ \epsilon ϵ：小常数（通常1e-8），防止除零
  • 问题： G t G_t Gt单调递增，学习率会趋向0

PyTorch实现：

python 复制代码 
import torch.optim as optim

# Adagrad
optimizer_adagrad = optim.Adagrad(
    model.parameters(),
    lr=0.01,                          # 学习率
    lr_decay=0,                        # 学习率衰减
    weight_decay=0,                    # 权重衰减（L2正则化）
    initial_accumulator_value=0,       # 初始累积值
    eps=1e-10                          # 数值稳定性常数
)

"""
参数说明：
- params: 要优化的参数，通常是model.parameters()
- lr: 学习率，控制每次更新的步长
- lr_decay: 学习率衰减，控制学习率的衰减速度
- weight_decay: 权重衰减系数（L2正则化），用于防止过拟合
- initial_accumulator_value: 初始累积值，控制累积的起始状态
- eps: 数值稳定性常数，防止除零错误
"""

2. RMSprop - 指数加权平均

数学公式 ：

RMSprop解决了Adagrad学习率衰减过快的问题，引入衰减系数：

E [ g 2 ] t = β E [ g 2 ] t − 1 + ( 1 − β ) g t 2 θ t + 1 = θ t − η E [ g 2 ] t + ϵ ⋅ g t \begin{aligned} E[g^2]t &= \beta E[g^2]{t-1} + (1 - \beta) g_t^2 \\ \theta_{t+1} &= \theta_t - \frac{\eta}{\sqrt{E[g^2]_t + \epsilon}} \cdot g_t \end{aligned} E[g2]tθt+1=βE[g2]t−1+(1−β)gt2=θt−E[g2]t+ϵ η⋅gt

参数说明：

  • E [ g 2 ] t E[g^2]_t E[g2]t：梯度平方的指数移动平均
  • β \beta β：衰减率，通常0.9
  • θ t \theta_t θt：第t次迭代时的模型参数
  • η \eta η：学习率
  • g t g_t gt：损失函数在 θ t \theta_t θt处的梯度
  • ϵ \epsilon ϵ：小常数（通常1e-8），防止除零

PyTorch实现：

python 复制代码 
import torch.optim as optim

# RMSprop
optimizer_rmsprop = optim.RMSprop(
    model.parameters(),
    lr=0.01,          # 学习率
    alpha=0.99,       # 平滑常数，对应公式中的β
    eps=1e-08,        # 数值稳定性常数
    weight_decay=0,   # 权重衰减（L2正则化）
    momentum=0,       # 动量
    centered=False    # 是否中心化
)

"""
参数说明：
- params: 要优化的参数，通常是model.parameters()
- lr: 学习率，控制每次更新的步长
- alpha: 平滑常数，控制梯度平方的指数移动平均
- eps: 数值稳定性常数，防止除零错误
- weight_decay: 权重衰减系数（L2正则化），用于防止过拟合
- momentum: 动量系数，若使用则启用动量
- centered: 是否使用中心化的RMSprop
"""

3. Adadelta - 自适应学习率

数学公式 ：

Adadelta进一步改进，不需要设置学习率：

E [ g 2 ] t = ρ E [ g 2 ] t − 1 + ( 1 − ρ ) g t 2 Δ θ t = − E [ Δ θ 2 ] t − 1 + ϵ E [ g 2 ] t + ϵ ⋅ g t E [ Δ θ 2 ] t = ρ E [ Δ θ 2 ] t − 1 + ( 1 − ρ ) Δ θ t 2 θ t + 1 = θ t + Δ θ t \begin{aligned} E[g^2]t &= \rho E[g^2]{t-1} + (1 - \rho) g_t^2 \\ \Delta\theta_t &= -\frac{\sqrt{E[\Delta\theta^2]_{t-1} + \epsilon}}{\sqrt{E[g^2]t + \epsilon}} \cdot g_t \\ E[\Delta\theta^2]t &= \rho E[\Delta\theta^2]{t-1} + (1 - \rho) \Delta\theta_t^2 \\ \theta{t+1} &= \theta_t + \Delta\theta_t \end{aligned} E[g2]tΔθtE[Δθ2]tθt+1=ρE[g2]t−1+(1−ρ)gt2=−E[g2]t+ϵ E[Δθ2]t−1+ϵ ⋅gt=ρE[Δθ2]t−1+(1−ρ)Δθt2=θt+Δθt

参数说明：

  • E [ g 2 ] t E[g^2]_t E[g2]t：梯度平方的指数移动平均
  • ρ \rho ρ：衰减率，通常0.9
  • g t g_t gt：损失函数在 θ t \theta_t θt处的梯度
  • E [ Δ θ 2 ] t E[\Delta\theta^2]_t E[Δθ2]t：参数更新量的平方的指数移动平均
  • Δ θ t \Delta\theta_t Δθt：参数更新量
  • θ t \theta_t θt：第t次迭代时的模型参数
  • ϵ \epsilon ϵ：小常数（通常1e-8），防止除零

PyTorch实现：

python 复制代码 
import torch.optim as optim

# Adadelta
optimizer_adadelta = optim.Adadelta(
    model.parameters(),
    lr=1.0,           # 注意：Adadelta中lr通常设为1.0
    rho=0.9,          # 衰减率
    eps=1e-06,        # 数值稳定性常数
    weight_decay=0    # 权重衰减（L2正则化）
)

"""
参数说明：
- params: 要优化的参数，通常是model.parameters()
- lr: 学习率，通常设为1.0
- rho: 衰减率，控制梯度平方的指数移动平均
- eps: 数值稳定性常数，防止除零错误
- weight_decay: 权重衰减系数（L2正则化），用于防止过拟合
"""

三、现代优化器

1. Adam - 自适应矩估计

数学公式 ：

Adam结合了动量法和RMSprop的优点：

m t = β 1 m t − 1 + ( 1 − β 1 ) g t （一阶矩估计） v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 （二阶矩估计） m ^ t = m t 1 − β 1 t （偏差校正） v ^ t = v t 1 − β 2 t （偏差校正） θ t + 1 = θ t − η v ^ t + ϵ ⋅ m ^ t \begin{aligned} m_t &= \beta_1 m_{t-1} + (1 - \beta_1) g_t &\text{（一阶矩估计）} \\ v_t &= \beta_2 v_{t-1} + (1 - \beta_2) g_t^2 &\text{（二阶矩估计）} \\ \hat{m}_t &= \frac{m_t}{1 - \beta_1^t} &\text{（偏差校正）} \\ \hat{v}t &= \frac{v_t}{1 - \beta_2^t} &\text{（偏差校正）} \\ \theta{t+1} &= \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \cdot \hat{m}_t \end{aligned} mtvtm^tv^tθt+1=β1mt−1+(1−β1)gt=β2vt−1+(1−β2)gt2=1−β1tmt=1−β2tvt=θt−v^t +ϵη⋅m^t（一阶矩估计）（二阶矩估计）（偏差校正）（偏差校正）

参数说明：

  • m t m_t mt：一阶矩估计（梯度指数加权平均）
  • v t v_t vt：二阶矩估计（梯度平方指数加权平均）
  • β 1 \beta_1 β1：一阶矩衰减率，通常0.9
  • β 2 \beta_2 β2：二阶矩衰减率，通常0.999
  • m ^ t \hat{m}_t m^t：一阶矩偏差校正
  • v ^ t \hat{v}_t v^t：二阶矩偏差校正
  • η \eta η：学习率
  • θ t \theta_t θt：第t次迭代时的模型参数
  • g t g_t gt：损失函数在 θ t \theta_t θt处的梯度
  • ϵ \epsilon ϵ：小常数（通常1e-8），防止除零
  • t t t：当前迭代次数

PyTorch实现：

python 复制代码 
import torch.optim as optim

# Adam
optimizer_adam = optim.Adam(
    model.parameters(),
    lr=0.001,            # 学习率
    betas=(0.9, 0.999),  # β1和β2
    eps=1e-08,           # 数值稳定性常数
    weight_decay=0,      # 权重衰减（L2正则化）
    amsgrad=False        # 是否使用AMSGrad变体
)

"""
参数说明：
- params: 要优化的参数，通常是model.parameters()
- lr: 学习率，控制每次更新的步长
- betas: 一阶和二阶矩估计的衰减率，通常设为(0.9, 0.999)
- eps: 数值稳定性常数，防止除零错误
- weight_decay: 权重衰减系数（L2正则化），用于防止过拟合
- amsgrad: 是否使用AMSGrad变体，若为True则启用AMSGrad
"""

2. AdamW - 解耦权重衰减

数学公式：

原始Adam（带权重衰减）：
θ t + 1 = θ t − η ( m ^ t v ^ t + ϵ + λ θ t ) \theta_{t+1} = \theta_t - \eta \left( \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon} + \lambda \theta_t \right) θt+1=θt−η(v^t +ϵm^t+λθt)

AdamW（解耦权重衰减）：
θ t + 1 = ( 1 − η λ ) θ t − η m ^ t v ^ t + ϵ \begin{aligned} \theta_{t+1} &= (1 - \eta \lambda) \theta_t - \eta \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon} \end{aligned} θt+1=(1−ηλ)θt−ηv^t +ϵm^t

参数说明：

  • θ t \theta_t θt：第t次迭代时的模型参数
  • η \eta η：学习率
  • λ \lambda λ：权重衰减系数
  • m ^ t \hat{m}_t m^t：一阶矩偏差校正
  • v ^ t \hat{v}_t v^t：二阶矩偏差校正
  • ϵ \epsilon ϵ：小常数（通常1e-8），防止除零
  • 改进：将权重衰减与梯度更新解耦，解决Adam中权重衰减与自适应学习率不兼容的问题

PyTorch实现：

python 复制代码 
import torch.optim as optim

# AdamW (推荐)
optimizer_adamw = optim.AdamW(
    model.parameters(),
    lr=0.001,            # 学习率
    betas=(0.9, 0.999),  # β1和β2
    eps=1e-08,           # 数值稳定性常数
    weight_decay=0.01,   # 解耦权重衰减
    amsgrad=False
)

"""
参数说明：
- params: 要优化的参数，通常是model.parameters()
- lr: 学习率，控制每次更新的步长
- betas: 一阶和二阶矩估计的衰减率，通常设为(0.9, 0.999)
- eps: 数值稳定性常数，防止除零错误
- weight_decay: 解耦权重衰减系数，通常用于防止过拟合
- amsgrad: 是否使用AMSGrad变体，若为True则启用AMSGrad
"""

总结

优化器 特点 适用场景 推荐参数
SGD 简单，收敛慢，易震荡 理论研究 lr=0.01
SGD with Momentum 加速收敛，减少震荡 计算机视觉 lr=0.01, momentum=0.9
NAG 动量法改进，更稳定 对稳定性要求高的任务 lr=0.01, momentum=0.9, nesterov=True
Adagrad 自适应学习率 稀疏数据 lr=0.01
RMSprop 解决Adagrad学习率衰减问题 非平稳目标 lr=0.001, alpha=0.99
Adadelta 无需学习率 不需要调学习率的任务 lr=1.0, rho=0.9
Adam 自适应矩估计 大多数深度学习任务 lr=0.001, betas=(0.9,0.999)
AdamW 解耦权重衰减 现代Transformer模型 lr=0.001, betas=(0.9,0.999), weight_decay=0.01
相关推荐
Aevget2 小时前
DevExpress JS & ASP.NET Core v25.1新版亮点 - 新增AI文本编辑功能
javascript·人工智能·asp.net·界面控件·devexpress·ui开发
3824278272 小时前
python:yield用法
开发语言·python
寻道模式2 小时前
【时间之外】创业踩坑指南（7）-方向盘哲学
人工智能·创业
智算菩萨2 小时前
未来家居可能的新变化：从“智能设备堆叠”到“自适应生活系统”
人工智能·生活
STLearner2 小时前
AAAI 2026 | 时空数据(Spatial-temporal)论文总结[下]（自动驾驶，天气预报，城市科学，POI推荐等）
人工智能·python·深度学习·机器学习·数据挖掘·自动驾驶·智慧城市
后端小张2 小时前
【AI 学习】LangChain框架深度解析：从核心组件到企业级应用实战
java·人工智能·学习·langchain·tensorflow·gpt-3·ai编程
NAGNIP2 小时前
LongCat-Flash-Omni：美团的全模态大模型
人工智能
未来之窗软件服务2 小时前
幽冥大陆(六十二) 多数据库交叉链接系统Go语言—东方仙盟筑基期
数据库·人工智能·oracle·golang·数据库集群·仙盟创梦ide·东方仙盟
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）05解决 WSL Ubuntu 中 /etc/resolv.conf 自动重置问题06Gemini3 生成的基于手势控制3D粒子圣诞树07Labelme从安装到标注：零基础完整指南08CentOS的ISO镜像下载09安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）10Multisim使用教程详尽版--(2025最新版)