一 水平集基本原理
水平集方法是一种用于跟踪运动界面 的数值方法,通过一个水平集函数 来表示界面位置。
和VOF方法相似,
=1 表示电解质区域,流体区域
=0 表示沉积的固体铜区域,固体区域
=0.5 的等值线即为界面,固液交接
适用于处理拓扑变化能力, 模拟空腔形成、合并、分裂 等复杂界面演化过程,适用于电沉积中可能出现的孔洞、缝隙,避免网格重构, 可与Nernst--Planck方程、Butler--Volmer动力学等电化学模型直接耦合,实现沉积过程的多物理场模拟。
| 对比项 | 水平集方法 | 变形几何方法 |
|---|---|---|
| 拓扑处理能力 | ✅ 支持 | ❌ 不支持 |
| 计算稳定性 | ✅ 高 | ⚠️ 空腔形成后中断 |
| 网格要求 | 固定网格 | 需移动/重构网格 |
| 模拟时间 | 可延长至20s | 约14s后停止 |
传统方法(变形几何)的局限性
传统使用"变形几何"节点来模拟电镀过程,但无法处理**拓扑变化,**一旦形成空腔(约14秒),计算就会停止,无法继续模拟后续过程。
二 仿真设置
(1)水平集设置窗口的"离散化"栏中水平集变量 ,决定了数学表达精度。

线性 (Linear): 每个网格单元内被假设为一条直线。
二次 (Quadratic): 每个网格单元内被假设为一个二次曲线
高次能够高精度地捕捉沉积界面的弯曲、演化以及最终的空腔形成过程,但加大了计算量,占用更多内存。
(2)水平集模型1
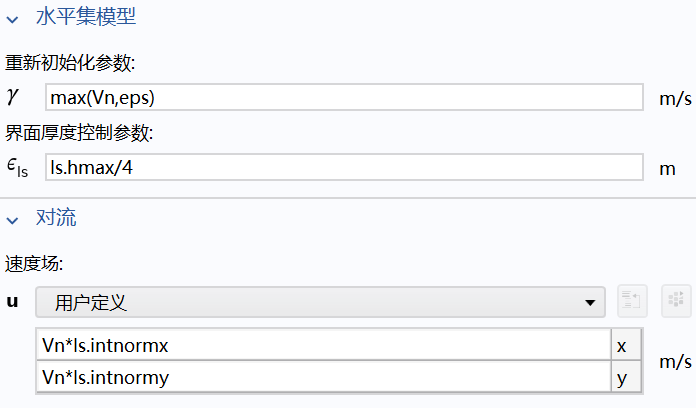
重新初始化参数意义 :重新初始化过程的速度应该至少与物理界面移动速度相当,甚至更快。这样才能确保在界面移动的同时,水平集函数能保持正确的梯度特性。
Vn :代表界面移动的物理速度大小
eps :一个很小的正数,确保 g 不为零
界面厚度控制参数 :定义了数值上界面的扩散厚度。实际界面是无限薄的,但数值计算需要一个有限厚度的过渡区。
ls.hmax :计算域中的最大网格单元尺寸
如果 太小(远小于网格尺寸),界面会变得过于尖锐,可能导致数值震荡和不稳定。
如果太大,界面过于模糊,无法精确定位,物理精度下降。
hmax/4 是一个经过验证的经验公式,在计算精度 和数值稳定性之间提供了良好的平衡。
速度场:自适应界面追踪 :随着界面的变形,ls.intnorm 会自动更新,确保沉积始终沿着当前的法向进行,即使界面变得高度弯曲或形成空腔。
Vn 是从电化学方程计算得到的物理量。
ls.intnorm 是从水平集变量计算得到的几何量。
电化学反应决定速度大小,界面几何决定速度方向。
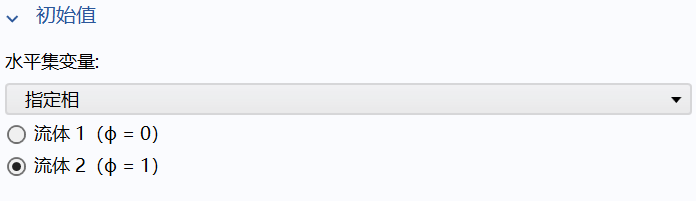
(3)初始值1:指定流体域和固体域
(4)选定入口出口
三 相场法基本原理
相场法和水平集方法都是用于追踪移动界面的方法
选择相场法(看重物理过程):
-
界面物理过程重要(如表面张力)
-
需要严格的质量守恒
-
模拟多相流与相分离耦合
-
研究界面稳定性、图案形成
选择 水平集法(看重几何变化):
-
主要关注几何演化
-
需要计算效率
-
处理大变形、拓扑变化
-
已有成熟的水平集模型框架
四 仿真设置
(1)离散化设置 - 选择二次
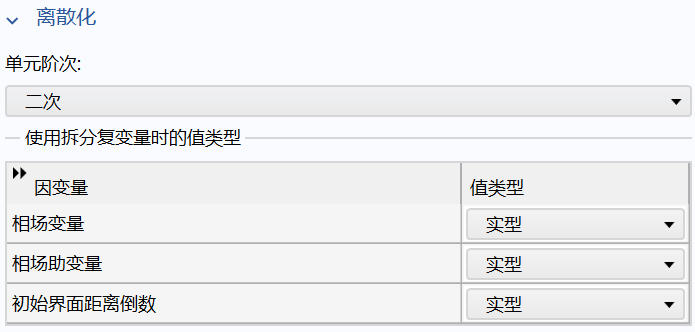
Cahn-Hilliard方程包含四阶导数 ,需要高阶形函数才能准确离散化,二次形函数提供连续的二阶导数,适合高阶PDE。
(2)相场模型1
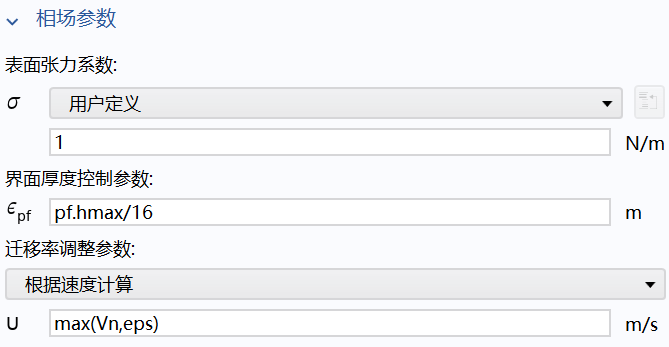
**界面厚度参数:**与表面张力相关,相比水平集更薄,可以准确描述相分离的尖锐界面。
**迁移率调整参数:**相场扩散的迁移率,根据速度计算
其余与水平集同理。
(3)设置出口入口
五 总结
对于电镀模拟:
两种PDE都能捕捉空腔形成:
-
水平集PDE更计算高效 ,适合工程应用(二阶非线性PDE)
-
相场PDE更物理丰富 ,适合机理研究(四阶非线性PDE)