文章目录
- 计算安全性
- 安全规约证明(重点)
- [对称加密的窃听不可区分实验(带n) (重点)](#对称加密的窃听不可区分实验(带n) (重点))
计算安全性
- 计算安全性弱于信息论安全性。它目前也依赖于假设,而实现后者不需要任何假设。
- 计算安全是大多数现代密码学构造方法的目标。
- 计算安全的方案,只要给足够的时间和计算能力总能被攻破!
- 使用完善保密的加密方案是不必要的。只要在实践上是不可破译的密码方案即可实用,如某方案在200年内,使用最快的可用的超级计算机,也不能以大于10^(−30)的概率攻破。
- 基于计算安全的方法包含两种放宽的完善安全概念:
- 对抗可行性时间内运行的敌手,安全性存在。
- 敌手成功率很小,以至于不关心是否真的存在。
计算安全的渐进度量方法
- 渐进方法的核心 :该方法基于复杂性理论,将敌手(攻击者)的运行时间与成功概率视为安全参数 n n n 的函数(而非具体数值)。密码方案包含安全参数 n n n,诚实双方初始化时选定 n n n,且假设敌手已知该 n n n,敌手的运行时间与成功概率均由 n n n 决定。
- 可行策略与多项式时间 :将"可行的策略"或"有效的算法"等同于在以 n n n 为参数的多项式时间内运行的概率算法(运行时间表示为 a ⋅ n c a \cdot n^c a⋅nc,其中 a , c a, c a,c 为常量)。诚实方需在多项式时间内运行,敌手虽可能计算能力更强(运行时间更长),但也在多项式时间内运行;超多项式时间的攻击策略因无现实意义而被忽略。
- 小的成功概率与可忽略性 :将"小的成功概率"等同于成功概率小于任何以 n n n 为参数的多项式倒数(即对任意常量 c c c,当 n n n 足够大时,概率小于 n − c n^{-c} n−c)。比任何多项式倒数增长更慢的函数称为"可忽略的(negligible)"。
假设方案安全时,敌手运行 n 3 n^3 n3 分钟攻破方案的概率为 2 40 ⋅ 2 − n 2^{40} \cdot 2^{-n} 240⋅2−n(该函数关于 n n n 可忽略)。不同 n n n 值下的情况:
- 当 n ≤ 40 n \leq 40 n≤40,敌手运行约6周( 40 3 40^3 403 分钟)时,攻破概率为1,此时 n n n 无实际意义;
- 当 n = 50 n = 50 n=50,敌手运行约3个月( 50 3 50^3 503 分钟)时,攻破概率约 1 / 1000 1/1000 1/1000,无法接受;
- 当 n = 500 n = 500 n=500,敌手运行超200年时,攻破概率仅为 2 − 500 2^{-500} 2−500。
计算安全的渐进安全度量方法
- 有效计算:在概率多项式时间内执行的计算。
- 可忽略的成功概率:对任意多项式 p p p,如果攻破该方案的概率渐进小于 1 p ( n ) \frac{1}{p(n)} p(n)1,则认为该方案安全,否则视为不安全。
定义 3.4
函数 f f f 为可忽略的,如果对于每个多项式 p ( ⋅ ) p(\cdot) p(⋅),存在一个 N N N,使得对于所有的整数 n > N n > N n>N,都满足
f ( n ) < 1 p ( n ) . f(n) < \frac{1}{p(n)}. f(n)<p(n)1.
等价的公式化的表述是:对所有常量 c c c,存在一个 N N N,使得对于所有的 n > N n > N n>N,满足
f ( n ) < n − c . f(n) < n^{-c}. f(n)<n−c.
为了方便记忆,上面的表述也可以陈述如下:对于任意多项式 p ( ⋅ ) p(\cdot) p(⋅) 以及所有足够大的 n n n 值,满足
f ( n ) < 1 p ( n ) . f(n) < \frac{1}{p(n)}. f(n)<p(n)1.
通常将一个可忽略函数表示为 negl \text{negl} negl。
命题 3.6
令 negl 1 \text{negl}_1 negl1 和 negl 2 \text{negl}_2 negl2 为可忽略函数。则
(1) 函数 negl 3 \text{negl}_3 negl3 被定义为 negl 3 ( n ) = negl 1 ( n ) + negl 2 ( n ) \text{negl}_3(n) = \text{negl}_1(n) + \text{negl}_2(n) negl3(n)=negl1(n)+negl2(n),则该函数是可忽略的。
(2) 对于任何正多项式 p p p,函数 negl 4 \text{negl}_4 negl4 被定义为 negl 4 ( n ) = p ( n ) ⋅ negl 1 ( n ) \text{negl}_4(n) = p(n) \cdot \text{negl}_1(n) negl4(n)=p(n)⋅negl1(n),则该函数是可忽略的。
安全规约证明(重点)
- PPT(Probabilistic Polynomial Time):概率多项式时间。
- 指定有效(概率多项式时间)敌手 A \mathcal{A} A 攻击方案 Π \Pi Π,其成功概率为 ε ( n ) \varepsilon(n) ε(n)。
- 构造"规约"算法 A ′ \mathcal{A}' A′,将 A \mathcal{A} A 作为子程序,解决难题 X \mathcal{X} X:
- A ′ \mathcal{A}' A′ 仅知 A \mathcal{A} A 想攻击 Π \Pi Π,对 A \mathcal{A} A 的内部工作一无所知;
- 对难题 X \mathcal{X} X 的输入实例 x x x, A ′ \mathcal{A}' A′ 模拟 Π \Pi Π 的实例,使 A \mathcal{A} A 与 Π \Pi Π 交互的分布, A \mathcal{A} A的分布和 A \mathcal{A} A 自身与 Π \Pi Π 交互的分布相同(或接近)。
- 若 A \mathcal{A} A 成功"攻破"模拟的 Π \Pi Π 实例,则 A ′ \mathcal{A}' A′ 解决 X \mathcal{X} X 的概率至少为多项式倒数 1 / p ( n ) 1/p(n) 1/p(n)。
- 若 ε ( n ) \varepsilon(n) ε(n) 非可忽略,则 A ′ \mathcal{A}' A′ 解决 X \mathcal{X} X 的概率为 ε ( n ) / p ( n ) \varepsilon(n)/p(n) ε(n)/p(n)(非可忽略)。因 A ′ \mathcal{A}' A′ 有效,存在有效算法以非可忽略概率解决 X \mathcal{X} X,与假设矛盾。
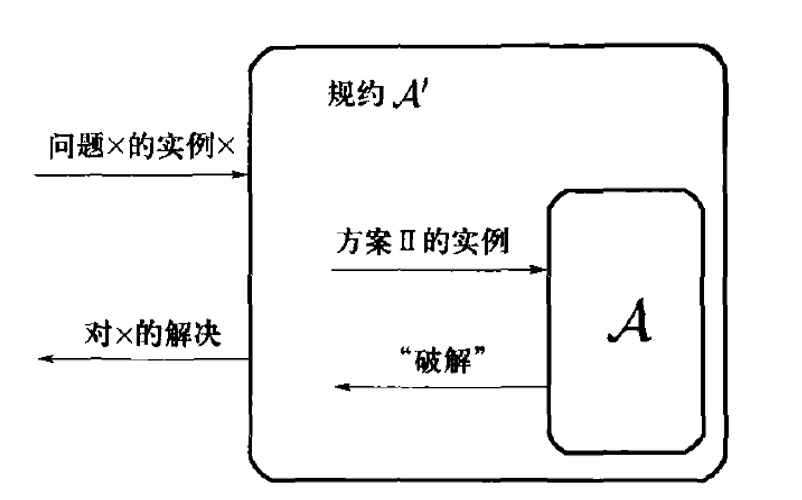
- 结论:给定难题 X \mathcal{X} X 的假设下,不存在有效敌手 A \mathcal{A} A 能以非可忽略概率攻破 Π \Pi Π,即 Π \Pi Π 是计算上安全的。
对称加密的窃听不可区分实验(带n) (重点)
- 窃听不可区分实验对任何对称密钥方案 π = ( G e n , E n c , D e c ) \pi =(Gen,Enc,Dec) π=(Gen,Enc,Dec),任何敌手 A \mathcal{A} A ,以及对任何安全参数 n n n的值都适用。
- 窃听不可区分实验 PrivK A , Π eav ( n ) : \text{PrivK}_{A,\Pi}^{\text{eav}}(n): PrivKA,Πeav(n):
- 给定输入 1 n 1^n 1n给敌手 A A A, A A A输出一对长度相等的消息 m 0 , m 1 m_0, m_1 m0,m1
- 运行 Gen ( 1 n ) \text{Gen}(1^n) Gen(1n) 生成一个密钥 k k k, 选择一个随机比特 b b b, b ← { 0 , 1 } b \leftarrow \{0,1\} b←{0,1}。一个密文 c ← Enc k ( m b ) c \leftarrow \text{Enc}_k(m_b) c←Enck(mb)被计算并且给 A A A。 把 c c c叫做挑战密文。
- A 输出一个比特 b ′ b' b′。
- 如果 b = b ′ b = b' b=b′, 则为1, 否则为 0 0 0。 如果 PrivK A , Π eav ( n ) = 14 \text{PrivK}_{A,\Pi}^{\text{eav}}(n) = 14 PrivKA,Πeav(n)=14, 则称 A A A成功。
定义 3.8
如果对于所有的概率多项式时间敌手 A \mathcal{A} A,存在一个可忽略函数 negl \text{negl} negl 使得:
Pr [ PrivK A , Π eav ( n ) = 1 ] ⩽ 1 2 + negl ( n ) \Pr\left[\text{PrivK}_{\mathcal{A},\Pi}^{\text{eav}}(n) = 1\right] \leqslant \frac{1}{2} + \text{negl}(n) Pr[PrivKA,Πeav(n)=1]⩽21+negl(n)
则一个对称密钥加密方案 Π = ( Gen , Enc , Dec ) \Pi = (\text{Gen}, \text{Enc}, \text{Dec}) Π=(Gen,Enc,Dec) 具备在窃听者存在的情况下不可区分的加密,其中概率的来源是 A \mathcal{A} A 的随机性以及实验的随机性。
定义 3.9
如果对于所有的概率多项式时间的敌手 A \mathcal{A} A,存在一个可忽略函数 negl \text{negl} negl 使得:
∣ Pr [ output ( PrivK A , Π eav ( n , 0 ) ) = 1 ] − Pr [ output ( PrivK A , Π eav ( n , 1 ) ) = 1 ] ∣ ⩽ negl ( n ) \left| \Pr\left[\text{output}\left(\text{PrivK}{\mathcal{A},\Pi}^{\text{eav}}(n,0)\right) = 1\right] - \Pr\left[\text{output}\left(\text{PrivK}{\mathcal{A},\Pi}^{\text{eav}}(n,1)\right) = 1\right] \right| \leqslant \text{negl}(n) Pr[output(PrivKA,Πeav(n,0))=1]−Pr[output(PrivKA,Πeav(n,1))=1] ⩽negl(n)
则对称密钥加密方案 Π = ( Gen , Enc , Dec ) \Pi = (\text{Gen}, \text{Enc}, \text{Dec}) Π=(Gen,Enc,Dec) 具有窃听者存在的情况下不可区分性。