渐进式GAN (ProGAN)：高分辨率图像生成的革命

回顾GAN的发展历程，我们看到了一条清晰的进化路径：

原始GAN (2014) - 开创对抗思想
│
├── DCGAN (2015) - 引入卷积结构，让图像生成成为可能
│
├── WGAN (2017) - 引入Wasserstein距离，解决训练不稳定
│
├── ProGAN (2017) - 渐进式训练，突破分辨率限制 
│
├── StyleGAN (2018) - 分离潜在空间，实现细粒度控制
│
├── StyleGAN2 (2019) - 改进架构，提升生成质量
│
├── StyleGAN3 (2021) - 引入等变性，解决纹理黏附
│
└── DragGAN (2023) - 交互式编辑，实现"所点即所得"

ProGAN （Progressive Growing of GANs）由Tero Karras等人于2017年提出，是首个能够稳定生成1024×1024高分辨率图像的生成对抗网络。在它之前，生成高分辨率图像如同攀登珠峰，既危险又困难；在它之后，高分辨率图像生成成为标准配置。

一、为什么需要渐进式训练？

1.1 高分辨率图像生成的三大挑战

在ProGAN出现之前，直接训练高分辨率GAN面临着几个难以逾越的障碍：

挑战	表现	后果
训练不稳定	梯度爆炸/消失，模式崩溃	模型完全无法学习
计算资源限制	高分辨率需要巨大显存	只能在低分辨率训练
细节生成困难	全局结构先于细节学习	生成的图像结构混乱

1.2 核心洞察：人类视觉的渐进性

回想一下我们是如何认识一个人的：

1. 先看到整体轮廓（是人是物？）
2. 再识别基本结构（五官位置？）
3. 然后注意细节特征（眼睛颜色？）
4. 最后把握纹理质感（皮肤细节？）

人类认知过程：
    [模糊轮廓] → [基本结构] → [细节特征] → [精细纹理]
    
机器学习同理：
    [4×4低分辨率] → [8×8基本结构] → [16×16细节] → [32×32纹理] → ...

二、ProGAN的核心思想：渐进式增长

2.1 渐进式训练流程

ProGAN的核心思想可以用一个简单的比喻来理解：教孩子画画。

1. 第一步：先教画简单的形状（4×4像素）
2. 第二步：在简单形状基础上添加细节（8×8像素）
3. 第三步：继续添加更精细的细节（16×16像素）
4. 重复直到完成高分辨率作品（1024×1024像素）

2.2 数学表达

生成器GGG由LLL个生成块组成：
G=GL∘GL−1∘⋯∘G1G = G_L \circ G_{L-1} \circ \cdots \circ G_1G=GL∘GL−1∘⋯∘G1

其中GiG_iGi处理分辨率2i+1×2i+12^{i+1} \times 2^{i+1}2i+1×2i+1的图像。

判别器DDD由LLL个判别块组成：
D=D1∘D2∘⋯∘DLD = D_1 \circ D_2 \circ \cdots \circ D_LD=D1∘D2∘⋯∘DL

其中DiD_iDi处理分辨率2i×2i2^{i} \times 2^{i}2i×2i的图像。

在第kkk个阶段训练时，目标函数为：
min⁡G1,...,Gkmax⁡D1,...,DkVk(D,G)=Ex∼pdata[log⁡D(k)(x)]+Ez∼pz[log⁡(1−D(k)(G(k)(z))] \min_{G_1,\ldots,G_k} \max_{D_1,\ldots,D_k} V_k(D,G) = \mathbb{E}{x \sim p{\text{data}}}[\log D^{(k)}(x)] + \mathbb{E}_{z \sim p_z}[\log(1 - D^{(k)}(G^{(k)}(z))] G1,...,GkminD1,...,DkmaxVk(D,G)=Ex∼pdata[logD(k)(x)]+Ez∼pz[log(1−D(k)(G(k)(z))]

其中G(k)=Gk∘⋯∘G1G^{(k)} = G_k \circ \cdots \circ G_1G(k)=Gk∘⋯∘G1，D(k)=D1∘⋯∘DkD^{(k)} = D_1 \circ \cdots \circ D_kD(k)=D1∘⋯∘Dk。

在从分辨率rkr_krk过渡到rk+1r_{k+1}rk+1时，引入混合参数α∈[0,1]\alpha \in [0,1]α∈[0,1]：

生成器输出混合 ：
xk+1=α⋅Gk+1(xk)+(1−α)⋅U(xk)x_{k+1} = \alpha \cdot G_{k+1}(x_k) + (1 - \alpha) \cdot U(x_k)xk+1=α⋅Gk+1(xk)+(1−α)⋅U(xk)

判别器输入混合 ：
Dinput=α⋅Dk+1(x)+(1−α)⋅Dk(Downsample(x))D_{\text{input}} = \alpha \cdot D_{k+1}(x) + (1 - \alpha) \cdot D_k(\text{Downsample}(x))Dinput=α⋅Dk+1(x)+(1−α)⋅Dk(Downsample(x))

其中UUU是上采样操作，α\alphaα从0线性增加到1。

渐进训练算法核心思想:逐步增加复杂度，每次只学习当前分辨率下的特征分布，稳定后增加分辨率继续学习更精细的特征。

1. 初始化：从4×4分辨率开始
2. 对于每个分辨率阶段k=1到L：
   a. 初始化混合参数α=0
   b. 在fade-in阶段（α从0到1）：
      - 生成器：混合新旧层输出
      - 判别器：混合新旧层输入
   c. α=1后，训练直到收敛
   d. 添加新分辨率层，进入下一阶段
3. 输出：高分辨率生成器G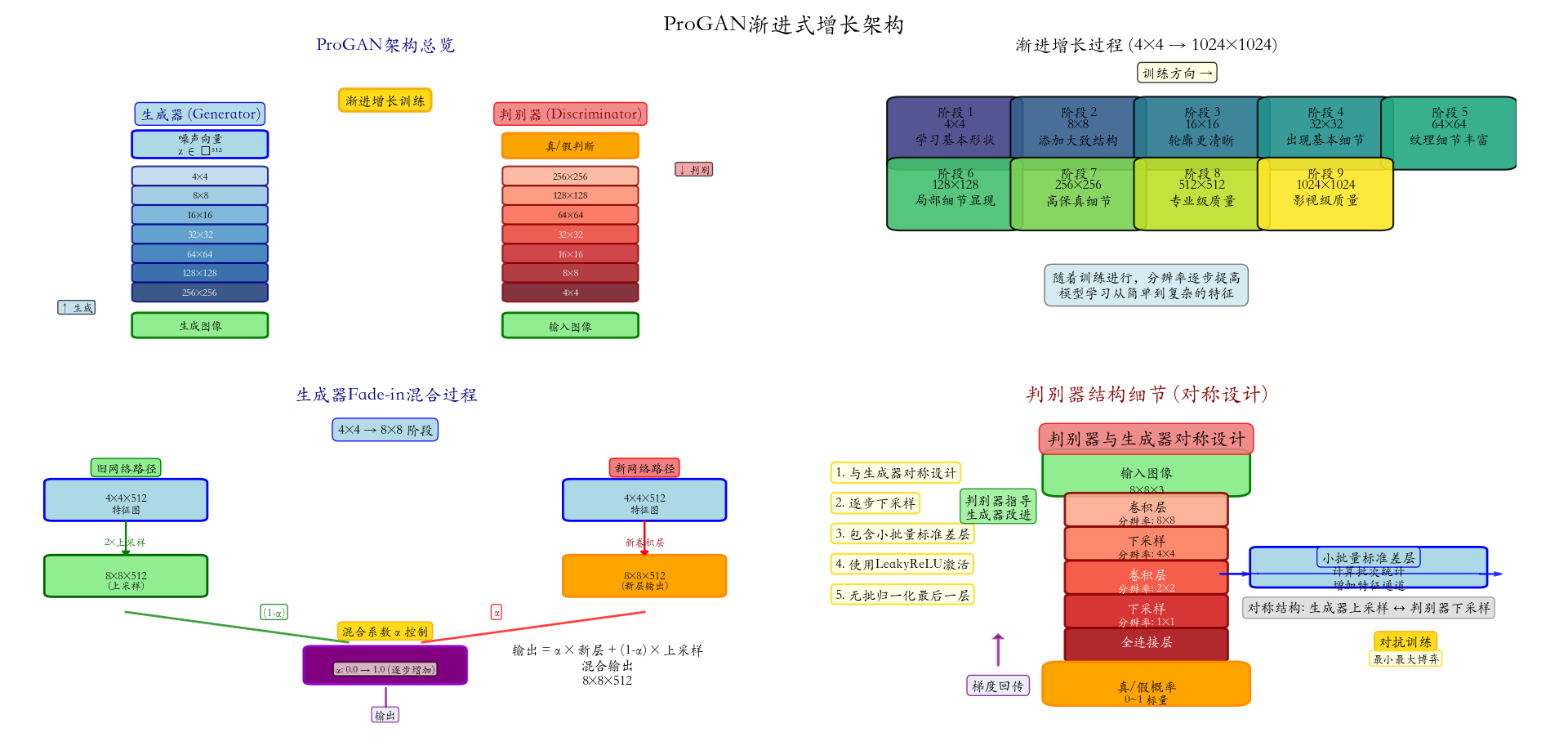

三、关键技术创新

3.1 平滑过渡（Fade-in）

渐进式训练的核心挑战之一是如何平滑地 从低分辨率过渡到高分辨率。ProGAN采用了创新的fade-in技术：

def fade_in_mixing(high_res_output, low_res_output, alpha):
    # alpha=0: 完全使用上采样的低分辨率输出
    # alpha=1: 完全使用新的高分辨率层输出
    mixed_output = alpha * high_res_output + (1 - alpha) * low_res_output
    return mixed_output

数学表达 ：
Output=α⋅Gnew+(1−α)⋅Upsample(Gold) \text{Output} = \alpha \cdot G_{\text{new}} + (1 - \alpha) \cdot \text{Upsample}(G_{\text{old}}) Output=α⋅Gnew+(1−α)⋅Upsample(Gold)

其中α\alphaα从0线性增加到1，实现平滑过渡。

3.2 小批量标准差（Minibatch Standard Deviation）

为了增加生成样本的多样性，防止模式崩溃，ProGAN引入了小批量标准差层，作用原理：

1. 计算每个空间位置的小批量标准差
2. 将标准差作为额外特征通道加入
3. 帮助判别器检测模式崩溃
4. 鼓励生成器产生多样化的输出

class MinibatchStdDev(nn.Module):
    """小批量标准差层 - 增加样本多样性"""
    
    def __init__(self, group_size=4, num_channels=1):
        super().__init__()
        self.group_size = group_size
        self.num_channels = num_channels
    
    def forward(self, x):
        batch_size, channels, height, width = x.shape
        
        # 如果批量大小小于组大小，返回原始输入
        if batch_size < self.group_size:
            return x
        
        # 重塑以计算组统计
        group_size = min(batch_size, self.group_size)
        
        # 计算小批量标准差
        y = x.reshape(group_size, -1, self.num_channels, height, width)
        y = y - y.mean(dim=0, keepdim=True)  # 减去组均值
        y = (y ** 2).mean(dim=0, keepdim=True)  # 计算方差
        y = (y + 1e-8).sqrt()  # 标准差，防止除零
        
        # 计算平均标准差
        y = y.mean(dim=[2, 3, 4], keepdim=True)
        y = y.repeat(group_size, 1, height, width)
        
        # 拼接回原始特征
        x = torch.cat([x, y], dim=1)
        
        return x

3.3 均等学习率（Equalized Learning Rate）

对于前向传播：
y=wTx y = w^T x y=wTx

如果 xxx 的方差为1，www 的元素独立同分布，方差为 σ2\sigma^2σ2，则：
Var(y)=fan_in×σ2 \text{Var}(y) = \text{fan\_in} \times \sigma^2 Var(y)=fan_in×σ2

为保持 yyy 的方差稳定，需要：
σ=1fan_in \sigma = \frac{1}{\sqrt{\text{fan\_in}}} σ=fan_in 1

ProGAN采用了均等学习率 技术，对权重进行特殊初始化。对于每个权重www，将其缩放为：
w′=w×cfan_in w' = w \times \frac{c}{\sqrt{\text{fan\_in}}} w′=w×fan_in c

其中ccc是常数，fan_in\text{fan\_in}fan_in是输入单元数。

优势：

1. 所有层的学习速度相同
2. 缓解梯度消失/爆炸
3. 提高训练稳定性

def equalized_lr(module, gain=1.0):
    """均等学习率初始化"""
    if hasattr(module, 'weight'):
        # 计算He初始化的标准差
        fan_in = module.weight.size(1) * module.weight[0][0].numel()
        std = gain / np.sqrt(fan_in)
        nn.init.normal_(module.weight, mean=0.0, std=std)
        module.weight.data *= np.sqrt(2) / np.sqrt(fan_in)
    
    if hasattr(module, 'bias') and module.bias is not None:
        nn.init.constant_(module.bias, 0.0)
    
    return module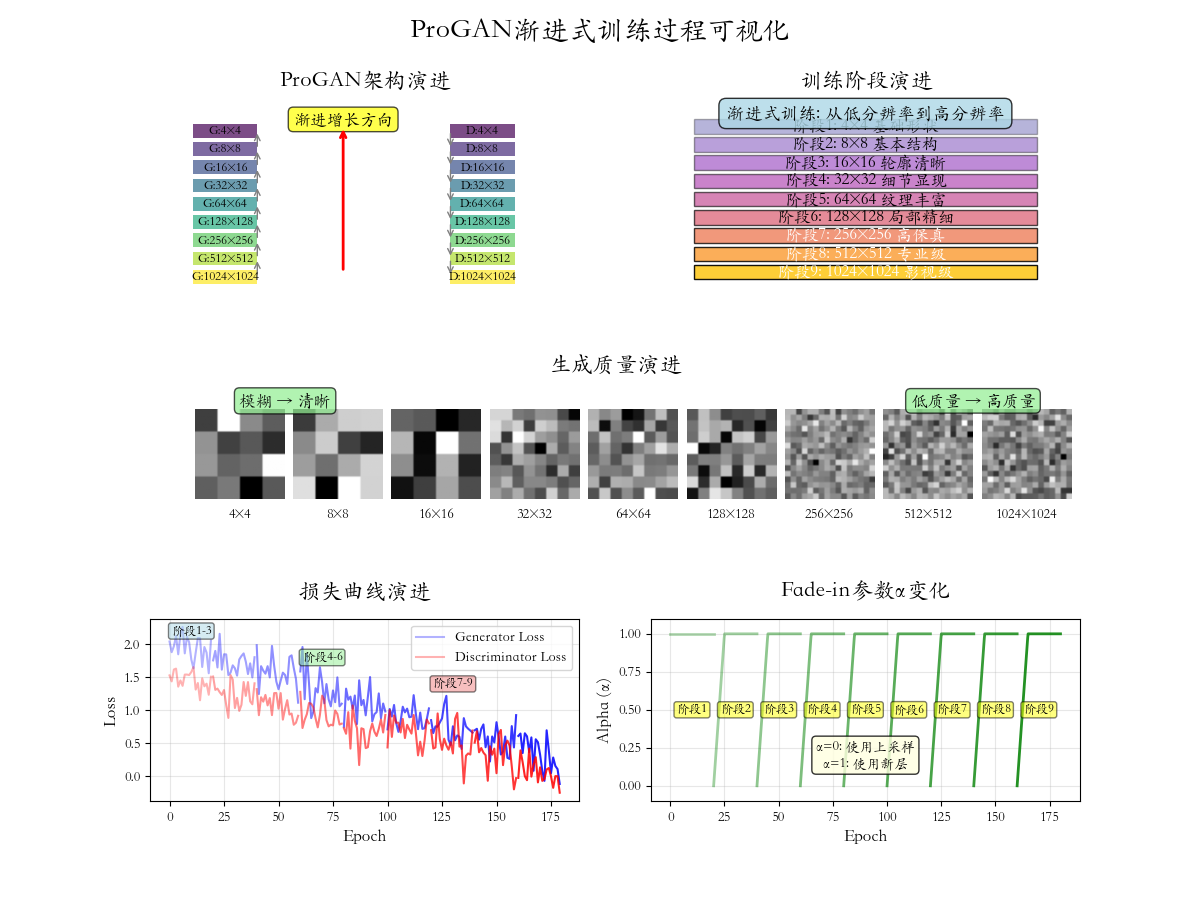

四、生成示例

import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import torch
from pytorch_pretrained_gans import make_gan

matplotlib.rcParams['axes.unicode_minus'] = False
matplotlib.rcParams['font.family'] = 'Kaiti SC'

# 1. 设置随机种子
seed = 40
torch.manual_seed(seed)
np.random.seed(seed)

# 2. 创建 BigGAN 模型
print("正在加载 BigGAN 模型...")
G = make_gan(gan_type='biggan', model_name='biggan-deep-512')
G.eval()  # 设置为评估模式

# 3. 生成随机噪声和类别标签
num_images = 8  # 生成的图像数量
z = G.sample_latent(batch_size=num_images)  # 随机噪声向量
y = G.sample_class(batch_size=num_images)  # 随机类别

# 4. 生成图像
print("生成图像中...")
with torch.no_grad():  # 不计算梯度，加快速度
    img_tensor = G(z=z, y=y)  # 生成图像张量

# 5. 处理图像格式
img_list = []
for i in range(num_images):
    img = img_tensor[i]  # 取第 i 张图片
    img = img.clamp(-1, 1)  # 限制在[-1, 1]范围
    img = (img + 1) / 2  # 转换到[0, 1]范围
    img = img.permute(1, 2, 0).numpy()  # 从 C×H×W 转换为 H×W×C
    img_list.append(img)

# 6. 保存和显示图像
print("保存图像...")
fig, axes = plt.subplots(2, 4, figsize=(16, 8))  # 创建 2x4 的子图
for ax, img in zip(axes.flatten(), img_list):
    ax.imshow(img)
    ax.axis('off')

plt.suptitle(f'BigGAN 生成的图像\n种子: {seed}', fontsize=16)
plt.savefig("biggan_generated_grid.png", bbox_inches='tight', dpi=300)
plt.show()

print("✅ 完成! 图像已保存为 'biggan_generated_grid.png'")