如上文所说,马尔可夫模型是一个简单好用的模型,日常中很多事问题也确实符合马尔可夫模型的要求,但有一个真严重的问题。对于一个问题,我们并不能直接观测到这个问题符合的马尔可夫模型的参数。比如下雨\晴天,实际生活中我们并不知道如果今天下雨,明天也下雨的真实概率是多少。因此我们需要方法来得到模型。
隐马尔可夫模型的三大问题
|-----------|-----------------------------------|
| 1. 概率计算问题 | 已知模型 + 观测序列,计算该序列出现的概率 |
| 2. 解码问题 | 已知模型 + 观测序列,找最可能的隐藏状态序列 |
| 3. 参数估计问题 | 已知观测序列,估计 HMM 的参数(初始 / 转移 / 发射概率) |
我们引言中提到的问题,就是第三类问题,也是最复杂的一种问题。下面我们仍然用下雨\晴天的例子来进行讨论三个问题。
例子
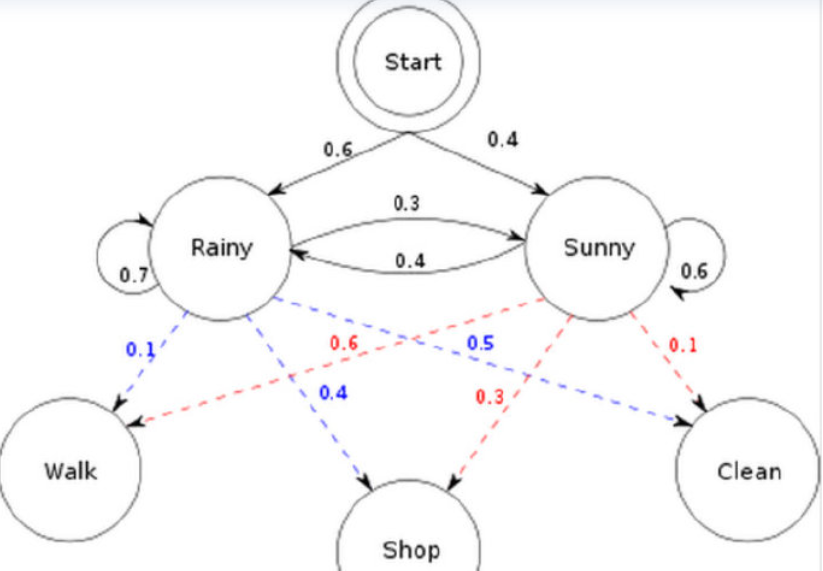
如图,问题1:已知整个模型,观测到连续三天做的事情是:散步,购物,收拾。那么,根据模型,计算产生这些行为的概率是多少。
问题2:同样知晓这个模型,同样是这三件事,我想猜,这三天的天气是怎么样的。
问题3:最复杂的,我只知道这三天做了这三件事,而其他什么信息都没有。我希望建立一个模型,求得模型的参数,即晴雨转换概率。
首先从图中提取 HMM 的基础参数(隐藏状态:Rainy (R)/Sunny (S);观测符号:Walk/Shop/Clean):

(这里应该是0.6,但是不影响思路,就不改了)
问题 1:概率计算(评估)------ 求 P (散步,购物,收拾 | 模型)


即 "散步、购物、收拾" 这个行为序列的生成概率约为 2.93%
问题 2:解码(预测)------ 求最可能的三天天气序列
该问题的求解方法是维特比算法(Viterbi Algorithm),也是卜老师算法课上重点介绍的算法,本文仅有一个简单例子辅助理解,本质上它的一种动态规划算法。(该算法推导涉及很多数学知识,推荐这篇文章Viterbi Algorithm)
| 符号 | 含义 | 本例取值 |
|---|---|---|
| 隐藏状态集合(如天气) | Q = {R(雨), S(晴)},N=2 | |
| 观测状态集合(如行为) | V = {W(散步), Sh(购物), C(收拾)},M=3 | |
| 观测序列(长度T) | O = [O_1=W, O_2=Sh, O_3=C],T=3 | |
| 初始概率:时刻 1 处于隐藏状态q_i的概率 | ||
| 转移概率:时刻t从状态q_i到t+1状态q_j的概率 | A_{R→R}=0.7, A_{R→S}=0.3; A_{S→R}=0.4, A_{S→S}=0.6 | |
| 发射概率:状态q_i生成观测v_k的概率 | B_{R→W}=0.1, B_{R→Sh}=0.4, B_{R→C}=0.5; B_{S→W}=0.5, B_{S→Sh}=0.3, B_{S→C}=0.1 | |
| 动态规划核心数组:时刻t处于状态q_i,且观测到O_1~O_t的最大概率 | 局部最优解,用于递推 | |
| 路径记录数组:时刻t处于状态q_i时,能得到 |
用于最终回溯路径 |
这里用到了HMM 的两个关键假设:
- 马尔可夫性 :隐藏状态的转移只依赖前一状态,与更早的状态无关。即
(转移概率)。
- 观测独立性 :当前观测只依赖当前隐藏状态,与其他状态 / 观测无关。即
(发射概率)。
再回顾 δ(t,j) 的定义(推导的起点):δ(t,j) = 时刻 t 处于隐藏状态 j,且观测到前 t 个观测序列 O₁~O_t 的 最大概率。用概率表达式写为:(遍历所有可能的前 t-1 个状态路径,取能生成 O₁~O_t 的最大联合概率)
我们从 δ(t,j) 的概率表达式出发,用 "概率乘法公式" 和 HMM 的两个假设逐步拆分:



知道序列最大概率如何计算后,我们就可以继续本问题

第一天 "雨且散步" 的最大概率是 0.06,"晴且散步" 的最大概率是 0.2(晴的概率更高)。


第二天 "雨且购物" 的最大概率是 0.032(来自第一天晴→雨),"晴且购物" 的最大概率是 0.036(来自第一天晴→晴)。

第三天 "雨且收拾" 的最大概率是 0.0112(来自第二天雨→雨),"晴且收拾" 的最大概率是 0.00216(来自第二天晴→晴)。


这个算法涉及的数学知识很多,大家理解这个问题再求解什么即可。
问题 3:学习(参数估计)------ 仅已知观测序列,反推模型参数
这是三个问题中最复杂的一个问题,本质是先瞎猜规则→用观测验证→调整规则→再验证→直到规则贴合观测的循环,因此只用简单的例子说明一下算法的过程:
假设你只看到朋友 3 天的行为:散步→购物→收拾,但不知道他的 "天气习惯"(比如:出门先看天气?下雨更爱购物?晴天爱散步?)------ 现在要反推这 3 个规则:
- 朋友第一天出门,默认下雨 / 晴天的概率(初始概率);
- 朋友从 "下雨→晴天""晴天→下雨" 的概率(转移概率);
- 下雨 / 晴天时,朋友做散步 / 购物 / 收拾的概率(发射概率)。
这个方法的核心是"猜 - 调 - 稳" 三步循环:
第一步:先 "瞎猜" 一套初始规则(随便定参数)
因为啥都不知道,先随便编一套规则:
- 初始概率:第一天 50% 下雨、50% 晴天;
- 转移概率:下雨→晴天概率 50%,晴天→下雨概率 50%;
- 发射概率:下雨时 30% 散步、30% 购物、40% 收拾;晴天时 50% 散步、30% 购物、20% 收拾。
第二步:用观测 "验" 这个规则(E 步:算可能性)
用刚才猜的规则,反推 "观测序列背后,每个时刻是下雨 / 晴天的概率"------ 相当于 "根据猜的规则,给观测'配'隐藏状态的可能性"。
比如:
- 第一天朋友散步了,用猜的规则算:"散步时是下雨的概率"=23%,"是晴天的概率"=77%;
- 第二天朋友购物了,算:"购物时是下雨的概率"=45%,"是晴天的概率"=55%;
- 还能算 "第一天下雨→第二天晴天的概率"=30%,"第一天晴天→第二天下雨的概率"=25%。
第三步:按可能性 "调" 规则(M 步:让规则更贴合观测)
用第二步算出来的 "概率",重新修改规则 ------ 让新规则更符合 "观测序列 + 刚才算的可能性"。
比如:
- 初始概率:第一天 "下雨概率 23%、晴天 77%"→把初始规则改成 "23% 下雨、77% 晴天";
- 转移概率:"下雨→晴天的概率 30%"→把转移规则改成 "下雨转晴天 30%";
- 发射概率:"下雨时散步的概率 23%"→把发射规则改成 "下雨对应散步 23%"。
第四步:循环 "验 - 调",直到规则 "稳" 了
重复第二步和第三步:用新规则再算可能性,再调规则......
比如:
- 第二次循环:用新规则算 "第一天散步是下雨的概率" 变成 20%,再调规则;
- 第三次循环:算出来的概率和上次差不多,规则也没怎么变 ------ 这就叫 "收敛" 了。
最终结果:稳定的规则就是反推出来的模型参数
循环到规则几乎不变时,这套规则就是 "仅靠观测序列反推出来的最优模型参数"------ 比如最终得到:
- 初始概率:60% 下雨、40% 晴天;
- 转移概率:下雨→晴天 30%、晴天→下雨 40%;
- 发射概率:下雨对应散步 10%、购物 40%;晴天对应散步 50%、购物 30%。
当然,具体是如何做到的就留给大家自行研究了。