文章目录
一、前言
正交频分复用 (Orthogonal Frequency Division Multiplexing, OFDM)因其对频率选择性衰落的天然适配性、实现复杂度可控以及与多种信道编码/多天线技术的良好兼容性,已成为宽带无线通信系统中常用的物理层基带体制之一。其核心思想是将高速数据流分解为并行的低速子流,并分别加载到一组相互正交的子载波上 ,从而将多径信道下的卷积干扰转化为频域逐子载波的复数增益作用。理想情况下,加入循环前缀(Cyclic Prefix, CP)后,线性卷积可在有效符号区间内等效为循环卷积,使得接收端能够通过 FFT 将系统模型写成简洁的逐子载波形式
Y ( k ) = H ( k ) X ( k ) + W ( k ) Y(k)=H(k)X(k)+W(k) Y(k)=H(k)X(k)+W(k)其中 X ( k ) X(k) X(k)、 Y ( k ) Y(k) Y(k) 分别为第 k k k 个子载波的发送与接收符号, H ( k ) H(k) H(k) 为信道频率响应, W ( k ) W(k) W(k) 为加性噪声项。这一表达式不仅为信道估计与均衡提供了明确的工程入口,也使得误比特率(BER)随 E b / N 0 E_b/N_0 Eb/N0 的性能评估更具可解释性。
在实际链路中,除加性白噪声(AWGN)外,多径瑞利衰落导致的频率选择性、均衡与估计误差的耦合,以及载波频偏(Carrier Frequency Offset, CFO)引入的子载波间干扰(ICI),都会显著影响系统性能。因此,一个"可复现、可扩展、可对照"的端到端仿真框架,对于理解 OFDM 的关键机制与工程权衡尤为重要。基于此,本文围绕一个完整的 OFDM 物理层仿真程序展开介绍,重点阐明其功能组织方式、关键参数配置逻辑与实验输出设计,为后续读者复现实验现象与开展二次扩展提供基础。
二、程序整体功能概述
该程序面向端到端链路仿真,按照"发送端---信道---接收端---性能统计---可视化 "的典型结构搭建,覆盖 OFDM 系统中最常用且最具教学价值的模块组合。发送端首先生成随机二进制比特序列,随后执行 QPSK 调制(并提供 16QAM 作为可选扩展),完成串并转换与子载波映射;在频域符号中插入固定导频并预留 DC 与保护带后,通过 IFFT 得到时域 OFDM 符号并添加 CP。信道部分不仅包括 AWGN 场景,还实现了多径瑞利衰落模型,并进一步叠加载波频偏以刻画子载波正交性破坏所造成的 ICI。接收端依次完成去 CP、FFT、子载波解映射,并采用 LS(最小二乘)进行导频信道估计 ,结合复数域插值获得全带宽信道响应估计 H ^ ( k ) \hat{H}(k) H^(k),最后分别实施 ZF 与 MMSE 均衡得到等化符号并完成解调判决,从而统计 BER 与输出多维度的性能图形。
从实验设计上,组织为若干相对独立但逻辑递进的子实验:首先在 AWGN 信道下对照理论 BER 曲线验证调制与噪声标定的正确性;随后引入多径瑞利信道,比较无均衡、ZF、MMSE 及"完美信道"参考下的性能差异;进一步通过"有 CP/无 CP"的对比实验直观展示 CP 对抑制符号间干扰(ISI)的必要性;再通过 CFO 场景揭示频偏导致的 BER 劣化与频谱泄露现象;最后在 PAPR 维度给出 OFDM 典型峰均比问题的统计特征,并引入削波作为简易抑制手段,输出 CCDF 曲线用于量化对比。
三、系统模型与关键参数设置
为保证仿真结果的可解释性与可复现性,程序采用固定随机种子并给出一套相对"标准"的 OFDM 参数组合。IFFT/FFT 点数设置为 N fft = 64 N_{\text{fft}}=64 Nfft=64,循环前缀长度为 N cp = 16 N_{\text{cp}}=16 Ncp=16,即 CP 占比为 1 / 4 1/4 1/4。该配置使得当信道最大离散时延满足 L max < N cp L_{\max}<N_{\text{cp}} Lmax<Ncp 时,接收端在去 CP 后可近似满足循环卷积条件,从而维持子载波正交性并避免显著 ISI。子载波资源分配方面,程序显式划分 DC 与保护带子载波,并在有效子载波上采用较高密度导频布置(约每 3--4 个子载波插入一个导频),导频符号固定为 (+1)(BPSK 形式),便于 LS 估计的稳定性与实现简洁性。对应地,导频处的 LS 估计为
H ^ ( k p ) = Y ( k p ) X ( k p ) , k p ∈ P \hat{H}(k_p)=\frac{Y(k_p)}{X(k_p)},\quad k_p\in\mathcal{P} H^(kp)=X(kp)Y(kp),kp∈P其中 P \mathcal{P} P 为导频集合。由于导频仅覆盖部分子载波,程序进一步对 H ^ ( k p ) \hat{H}(k_p) H^(kp) 的实部与虚部分别进行线性插值,以获得全带宽估计 H ^ ( k ) \hat{H}(k) H^(k)。该策略在工程实现中常见,能够在复杂度与精度之间取得折中,并为后续均衡提供连续的频域信道响应。
均衡部分同时实现 ZF 与 MMSE 两种经典方案 。ZF 等化直接对每个数据子载波执行
X ^ ZF ( k ) = Y ( k ) H ^ ( k ) \hat{X}{\text{ZF}}(k)=\frac{Y(k)}{\hat{H}(k)} X^ZF(k)=H^(k)Y(k)其优点是形式简单,但在深衰落子载波处会放大噪声。MMSE 等化在此基础上引入噪声功率项 σ 2 \sigma^2 σ2 抑制噪声增强效应,可写为
X ^ MMSE ( k ) = H ^ ∗ ( k ) ∣ H ^ ( k ) ∣ 2 + σ 2 Y ( k ) \hat{X}{\text{MMSE}}(k)=\frac{\hat{H}^*(k)}{|\hat{H}(k)|^2+\sigma^2}Y(k) X^MMSE(k)=∣H^(k)∣2+σ2H^∗(k)Y(k)
其中 ( ⋅ ) ∗ (\cdot)^* (⋅)∗ 表示共轭。通过对比两者 BER 曲线,可直观观察到 ZF 与 MMSE 在中低信噪比与深衰落条件下的性能差异。
仿真指标以 E b / N 0 E_b/N_0 Eb/N0 为横轴,范围取 0--24 dB,并按调制阶数将其转换为符号域信噪比:对于 M M M 阶调制, k = log 2 M k=\log_2 M k=log2M,有
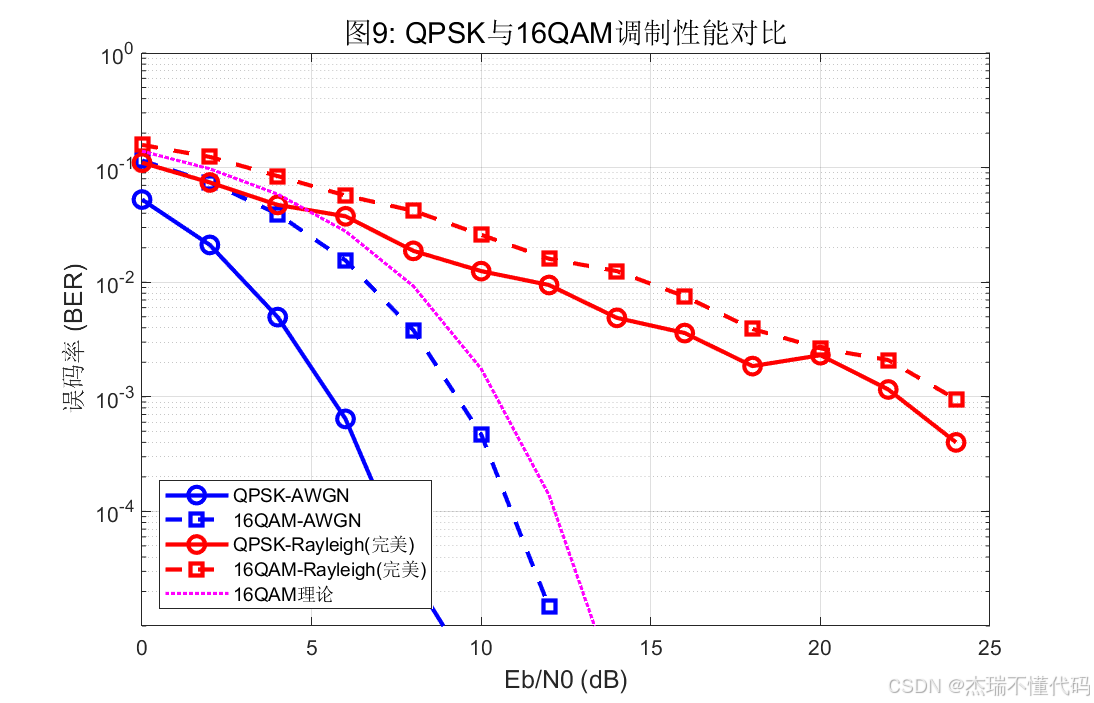
E s N 0 = E b N 0 + 10 log 10 ( k ) \frac{E_s}{N_0}=\frac{E_b}{N_0}+10\log_{10}(k) N0Es=N0Eb+10log10(k)程序在 QPSK ( k = 2 ) (k=2) (k=2)与 16QAM( k = 4 k=4 k=4)两种模式下均遵循该转换关系。为了使 BER 统计具有足够稳定性,程序采用"100 个 OFDM 符号/帧 × 50 帧"的 Monte-Carlo 结构进行平均,兼顾运算量与统计可靠性。
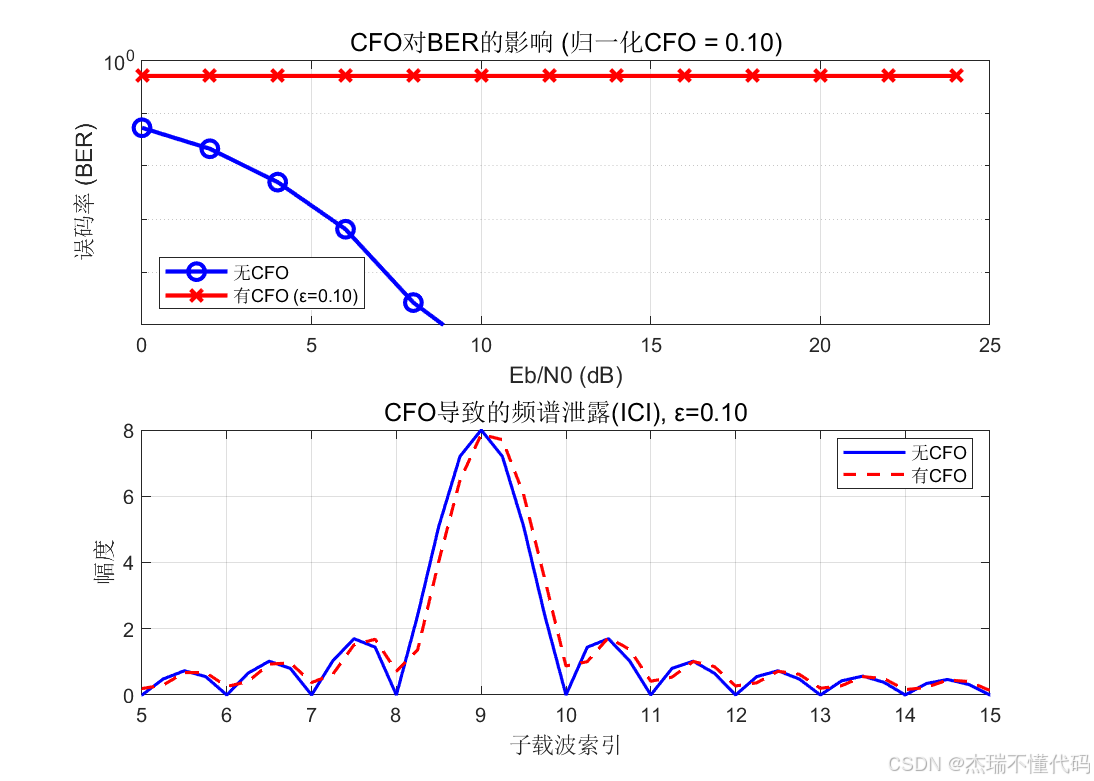
信道模型方面,除 AWGN 基线外,程序构建了多径瑞利衰落信道,采用离散多径冲激响应并对各路径引入复高斯衰落系数 ;在 CP 作用验证实验中进一步设置"最大时延略小于 CP 但足以引起明显频率选择性"的场景,并额外构造无 CP 的接收处理链路,从而将 ISI 对 BER 的影响以对照方式呈现。CFO 场景引入归一化频偏 ε = Δ f / Δ f sub \varepsilon=\Delta f/\Delta f_{\text{sub}} ε=Δf/Δfsub,其中 Δ f sub = f s / N fft \Delta f_{\text{sub}}=f_s/N_{\text{fft}} Δfsub=fs/Nfft 为子载波间隔。CFO 会破坏理想正交条件并产生 ICI,使得频域模型不再严格满足逐子载波独立的形式,进而导致 BER 明显劣化;程序同时通过频谱泄露示例对该现象进行可视化说明。最后,针对 OFDM 的 PAPR 问题,程序给出 PAPR 的定义
P A P R = 10 log 10 ( max n ∣ x ( n ) ∣ 2 E [ ∣ x ( n ) ∣ 2 ] ) \mathrm{PAPR}=10\log_{10}\left(\frac{\max_n |x(n)|^2}{\mathbb{E}[|x(n)|^2]}\right) PAPR=10log10(E[∣x(n)∣2]maxn∣x(n)∣2)
并采用削波比(相对 RMS 幅度)作为简易抑制手段,对比削波前后 PAPR 的统计均值、最大值及 CCDF 曲线,从而为"性能---实现复杂度---非线性失真"之间的权衡提供直观依据。
以上三部分构成了本文的技术铺垫 :在统一的 OFDM 参数框架下,通过 AWGN 校准、多径衰落估计与均衡、CP 与 CFO 的机理验证,以及 PAPR 的统计分析,程序能够输出一组覆盖面较完整的实验图形(BER 曲线、星座图、信道频响估计图、CP 对比、CFO 影响与 PAPR CCDF 等)。
四、关键代码片段
1、仿真1: AWGN信道下的BER
matlab
for snrIdx = 1:numEbN0
EbN0 = params.EbN0_dB(snrIdx);
% AWGN仿真:直接使用Es/N0 = Eb/N0 + 10*log10(k)
% 不需要额外的子载波比例修正,因为噪声是在时域整体加的
% 而FFT后噪声功率会均匀分布到各子载波
EsN0 = EbN0 + 10*log10(k_qpsk);
totalErrors = 0;
totalBits = 0;
for frame = 1:params.numFrames
% 生成随机比特
numBitsPerSymbol = numDataCarriers * k_qpsk;
numBits = numBitsPerSymbol * params.numSymbols;
txBits = randi([0 1], 1, numBits);
% 调制
txSymbols = qammod_custom(txBits, params.modOrder);
txSymbols = reshape(txSymbols, numDataCarriers, params.numSymbols);
% 子载波映射
freqSymbols = subcarrier_map(txSymbols, params.pilotSymbol, ...
params.dataIdx, params.pilotIdx, params.Nfft);
% OFDM调制
txSignal = ofdm_mod(freqSymbols, params.Nfft, params.Ncp);
% AWGN信道 - 使用Es/N0
rxSignal = add_awgn(txSignal, EsN0);
% OFDM解调
rxFreqSymbols = ofdm_demod(rxSignal, params.Nfft, params.Ncp, params.numSymbols);
% 子载波解映射
[rxDataSymbols, ~] = subcarrier_demap(rxFreqSymbols, params.dataIdx, params.pilotIdx);
% 解调
rxSymbolsVec = rxDataSymbols(:).';
rxBits = qamdemod_custom(rxSymbolsVec, params.modOrder);
% 统计误码
totalErrors = totalErrors + sum(txBits ~= rxBits);
totalBits = totalBits + numBits;
end
BER_AWGN(snrIdx) = totalErrors / totalBits;
fprintf('Eb/N0 = %2d dB, BER = %.2e\n', EbN0, BER_AWGN(snrIdx));
end2、仿真2: 多径瑞利信道
matlab
for snrIdx = 1:numEbN0
EbN0 = params.EbN0_dB(snrIdx);
EsN0 = EbN0 + 10*log10(k_qpsk);
errors_noEQ = 0;
errors_ZF = 0;
errors_MMSE = 0;
errors_perfect = 0;
totalBits = 0;
for frame = 1:params.numFrames
% 生成随机比特
numBitsPerSymbol = numDataCarriers * k_qpsk;
numBits = numBitsPerSymbol * params.numSymbols;
txBits = randi([0 1], 1, numBits);
% 调制
txSymbols = qammod_custom(txBits, params.modOrder);
txSymbols = reshape(txSymbols, numDataCarriers, params.numSymbols);
% 子载波映射
freqSymbols = subcarrier_map(txSymbols, params.pilotSymbol, ...
params.dataIdx, params.pilotIdx, params.Nfft);
% OFDM调制
txSignal = ofdm_mod(freqSymbols, params.Nfft, params.Ncp);
% 多径瑞利信道
[rxSignal, H_true] = rayleigh_channel(txSignal, params.pathDelays, ...
params.pathGains, params.sampleRate, params.Nfft);
% 添加噪声
rxSignal = add_awgn(rxSignal, EsN0);
% OFDM解调
rxFreqSymbols = ofdm_demod(rxSignal, params.Nfft, params.Ncp, params.numSymbols);
% 子载波解映射
[rxDataSymbols, rxPilotSymbols] = subcarrier_demap(rxFreqSymbols, ...
params.dataIdx, params.pilotIdx);
% 信道估计 (LS + 复数插值)
H_est_LS = ls_channel_estimation_complex(rxPilotSymbols(:,1), ...
params.pilotSymbol * ones(length(params.pilotIdx), 1), ...
params.pilotIdx, params.Nfft);
% 存储信道估计数据 (仅第一帧,中等SNR)
if frame == 1 && snrIdx == 7 % Eb/N0=12dB时存储
H_true_store = H_true;
H_est_LS_store = H_est_LS;
end
% 无均衡
rxSymbolsVec_noEQ = rxDataSymbols(:).';
rxBits_noEQ = qamdemod_custom(rxSymbolsVec_noEQ, params.modOrder);
errors_noEQ = errors_noEQ + sum(txBits ~= rxBits_noEQ);
% ZF均衡 (使用估计信道)
rxDataSymbols_ZF = zeros(size(rxDataSymbols));
H_data = H_est_LS(params.dataIdx);
for symIdx = 1:params.numSymbols
rxDataSymbols_ZF(:, symIdx) = rxDataSymbols(:, symIdx) ./ H_data;
end
rxSymbolsVec_ZF = rxDataSymbols_ZF(:).';
rxBits_ZF = qamdemod_custom(rxSymbolsVec_ZF, params.modOrder);
errors_ZF = errors_ZF + sum(txBits ~= rxBits_ZF);
% MMSE均衡
rxDataSymbols_MMSE = zeros(size(rxDataSymbols));
sigma2 = 1 / (10^(EsN0/10));
for symIdx = 1:params.numSymbols
rxDataSymbols_MMSE(:, symIdx) = conj(H_data) .* rxDataSymbols(:, symIdx) ./ (abs(H_data).^2 + sigma2);
end
rxSymbolsVec_MMSE = rxDataSymbols_MMSE(:).';
rxBits_MMSE = qamdemod_custom(rxSymbolsVec_MMSE, params.modOrder);
errors_MMSE = errors_MMSE + sum(txBits ~= rxBits_MMSE);
% 完美信道估计 + ZF均衡
rxDataSymbols_perfect = zeros(size(rxDataSymbols));
H_true_data = H_true(params.dataIdx);
for symIdx = 1:params.numSymbols
rxDataSymbols_perfect(:, symIdx) = rxDataSymbols(:, symIdx) ./ H_true_data;
end
rxSymbolsVec_perfect = rxDataSymbols_perfect(:).';
rxBits_perfect = qamdemod_custom(rxSymbolsVec_perfect, params.modOrder);
errors_perfect = errors_perfect + sum(txBits ~= rxBits_perfect);
% 存储星座图数据
if snrIdx == 7 && frame == 1
constellation_tx = txSymbols(:);
constellation_rx_noEQ = rxDataSymbols(:);
constellation_rx_EQ = rxDataSymbols_perfect(:); % 使用完美均衡的结果
end
totalBits = totalBits + numBits;
end
BER_Rayleigh_noEQ(snrIdx) = errors_noEQ / totalBits;
BER_Rayleigh_ZF(snrIdx) = errors_ZF / totalBits;
BER_Rayleigh_MMSE(snrIdx) = errors_MMSE / totalBits;
BER_Rayleigh_perfect(snrIdx) = errors_perfect / totalBits;
fprintf('Eb/N0 = %2d dB, BER(无均衡)=%.2e, BER(ZF)=%.2e, BER(MMSE)=%.2e, BER(完美)=%.2e\n', ...
EbN0, BER_Rayleigh_noEQ(snrIdx), BER_Rayleigh_ZF(snrIdx), ...
BER_Rayleigh_MMSE(snrIdx), BER_Rayleigh_perfect(snrIdx));
end3、仿真3: CP作用验证
matlab
for snrIdx = 1:numEbN0
EbN0 = params.EbN0_dB(snrIdx);
EsN0 = EbN0 + 10*log10(k_qpsk);
errors_noCP = 0;
totalBits = 0;
for frame = 1:params.numFrames
% 生成随机比特
numBitsPerSymbol = numDataCarriers * k_qpsk;
numBits = numBitsPerSymbol * params.numSymbols;
txBits = randi([0 1], 1, numBits);
% 调制
txSymbols = qammod_custom(txBits, params.modOrder);
txSymbols = reshape(txSymbols, numDataCarriers, params.numSymbols);
% 子载波映射
freqSymbols = subcarrier_map(txSymbols, params.pilotSymbol, ...
params.dataIdx, params.pilotIdx, params.Nfft);
% OFDM调制 (无CP)
txSignal_noCP = ofdm_mod(freqSymbols, params.Nfft, 0);
% 多径信道 - 使用专门的无CP信道函数,保留ISI
[rxSignal_noCP, H_true] = rayleigh_channel_noCP(txSignal_noCP, pathDelays_cp, ...
pathGains_cp, params.sampleRate, params.Nfft);
% 添加噪声
rxSignal_noCP = add_awgn(rxSignal_noCP, EsN0);
% OFDM解调 (无CP) - 直接取前Nfft点,会包含ISI
rxFreqSymbols_noCP = ofdm_demod_noCP(rxSignal_noCP, params.Nfft, params.numSymbols);
% 子载波解映射
[rxDataSymbols_noCP, rxPilotSymbols_noCP] = subcarrier_demap(rxFreqSymbols_noCP, ...
params.dataIdx, params.pilotIdx);
% 信道估计 (即使有ISI也尝试估计)
H_est = ls_channel_estimation_complex(rxPilotSymbols_noCP(:,1), ...
params.pilotSymbol * ones(length(params.pilotIdx), 1), ...
params.pilotIdx, params.Nfft);
% ZF均衡
rxDataSymbols_noCP_eq = zeros(size(rxDataSymbols_noCP));
H_data = H_est(params.dataIdx);
for symIdx = 1:params.numSymbols
rxDataSymbols_noCP_eq(:, symIdx) = rxDataSymbols_noCP(:, symIdx) ./ H_data;
end
% 解调
rxSymbolsVec = rxDataSymbols_noCP_eq(:).';
rxBits = qamdemod_custom(rxSymbolsVec, params.modOrder);
errors_noCP = errors_noCP + sum(txBits ~= rxBits);
totalBits = totalBits + numBits;
end
BER_noCP(snrIdx) = errors_noCP / totalBits;
fprintf('Eb/N0 = %2d dB, BER(无CP) = %.2e\n', EbN0, BER_noCP(snrIdx));
end
% 有CP的情况使用相同的信道重新计算
BER_withCP_longDelay = zeros(1, numEbN0);
for snrIdx = 1:numEbN0
EbN0 = params.EbN0_dB(snrIdx);
EsN0 = EbN0 + 10*log10(k_qpsk);
errors_withCP = 0;
totalBits = 0;
for frame = 1:params.numFrames
numBitsPerSymbol = numDataCarriers * k_qpsk;
numBits = numBitsPerSymbol * params.numSymbols;
txBits = randi([0 1], 1, numBits);
txSymbols = qammod_custom(txBits, params.modOrder);
txSymbols = reshape(txSymbols, numDataCarriers, params.numSymbols);
freqSymbols = subcarrier_map(txSymbols, params.pilotSymbol, ...
params.dataIdx, params.pilotIdx, params.Nfft);
% OFDM调制 (有CP)
txSignal = ofdm_mod(freqSymbols, params.Nfft, params.Ncp);
% 多径信道 (使用相同时延) - 有CP时用标准函数
[rxSignal, H_true] = rayleigh_channel(txSignal, pathDelays_cp, ...
pathGains_cp, params.sampleRate, params.Nfft);
rxSignal = add_awgn(rxSignal, EsN0);
rxFreqSymbols = ofdm_demod(rxSignal, params.Nfft, params.Ncp, params.numSymbols);
[rxDataSymbols, rxPilotSymbols] = subcarrier_demap(rxFreqSymbols, ...
params.dataIdx, params.pilotIdx);
H_est = ls_channel_estimation_complex(rxPilotSymbols(:,1), ...
params.pilotSymbol * ones(length(params.pilotIdx), 1), ...
params.pilotIdx, params.Nfft);
rxDataSymbols_eq = zeros(size(rxDataSymbols));
H_data = H_est(params.dataIdx);
for symIdx = 1:params.numSymbols
rxDataSymbols_eq(:, symIdx) = rxDataSymbols(:, symIdx) ./ H_data;
end
rxSymbolsVec = rxDataSymbols_eq(:).';
rxBits = qamdemod_custom(rxSymbolsVec, params.modOrder);
errors_withCP = errors_withCP + sum(txBits ~= rxBits);
totalBits = totalBits + numBits;
end
BER_withCP_longDelay(snrIdx) = errors_withCP / totalBits;
end五、实验仿真结果
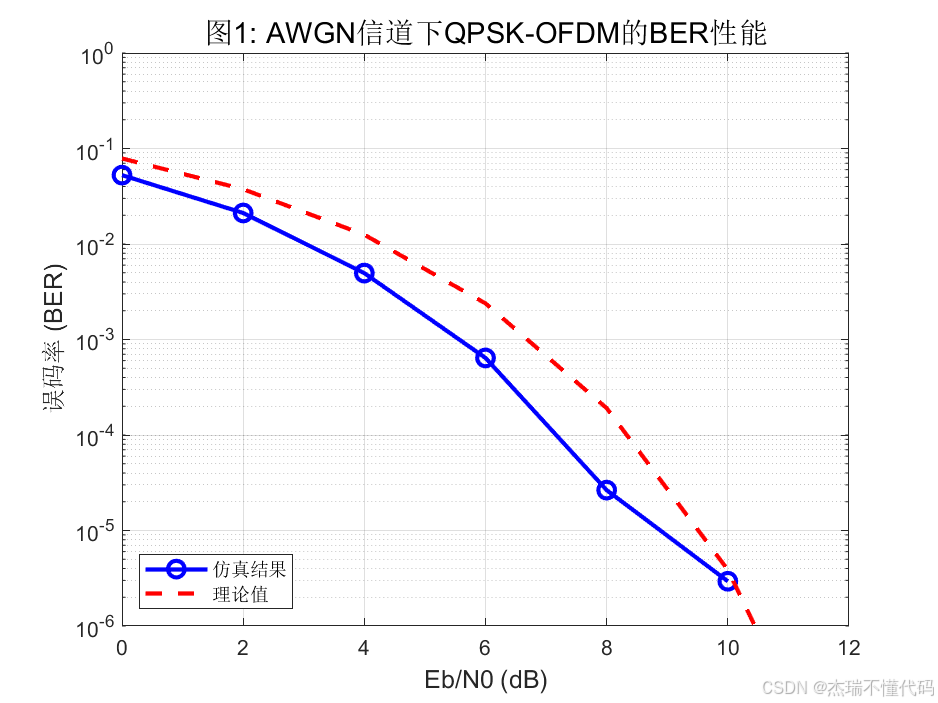
AWGN信道下QPSK-OFDM的BER性能(仿真vs理论)
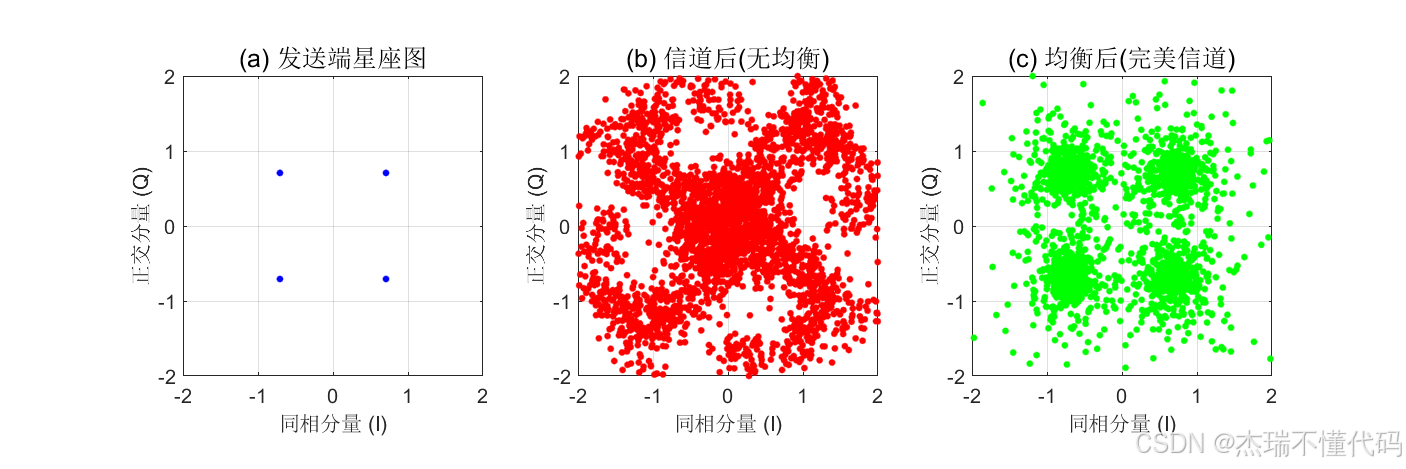
星座图对比(发送端/信道后/均衡后)
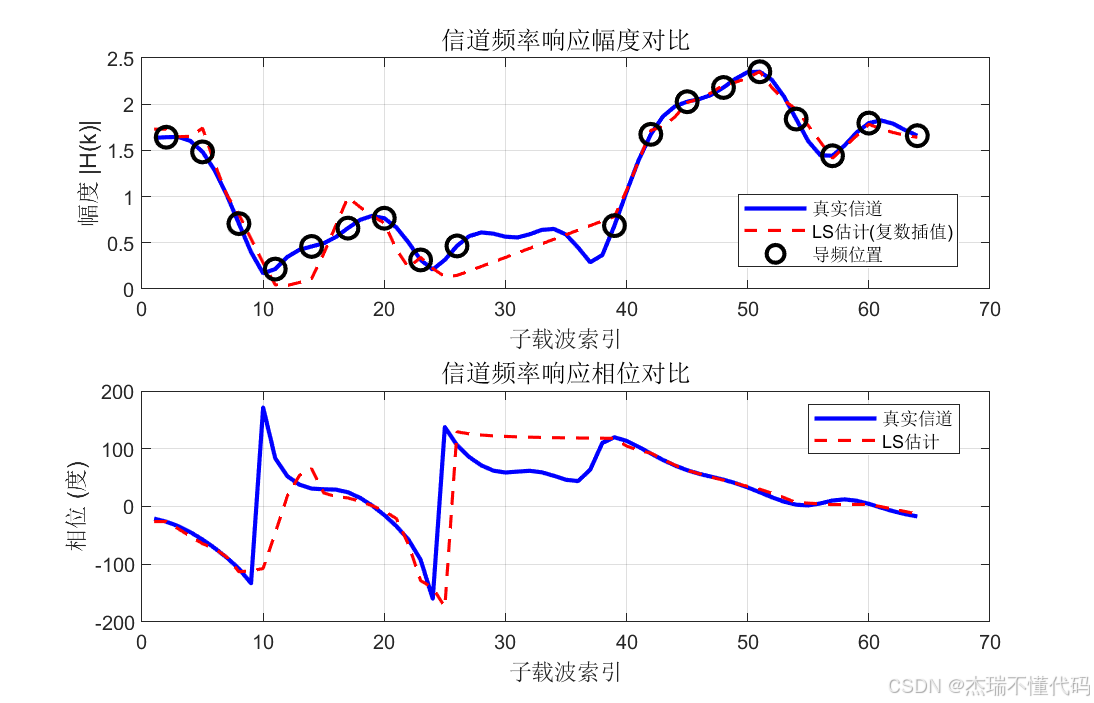
信道频率响应估计对比(真实vs LS估计)
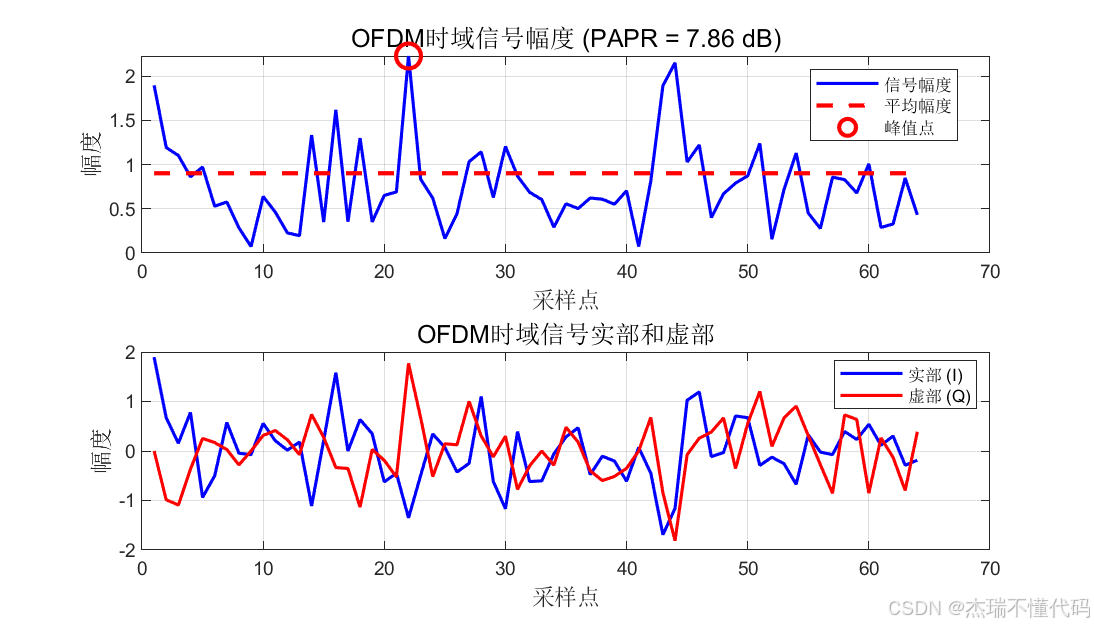
OFDM时域波形及PAPR展示
CFO对BER和频谱泄露的影响
QPSK与16QAM调制性能对比
由于源代码很长,无法直接全部粘在这,因此挑了一些关键的部分予以展示,如果你对完整源码、可运行工程文件或拓展版本 感兴趣,欢迎留言交流,后续也会继续分享更多通信系统仿真相关内容,我是不懂代码的杰瑞学长,我们下期再见!
如果觉得文章对你有帮助,欢迎点赞 + 收藏 + 关注,一起进步!