一、引言
随着大模型应用的爆发,向量数据库成为支撑语义检索、图像相似性匹配、推荐系统等场景的核心基础设施。向量索引作为向量数据库的性能引擎,其算法选择直接决定了查询效率与召回率的平衡。
传统的向量索引使用方式存在显著痛点,通常我们需要根据经验手动选择索引算法(如 HNSW、IVF-Flat、FAISS 等),并反复调优参数。但现实场景中,向量数据的特征(维度、分布、规模)千差万别,高维稀疏向量与低维稠密向量、百万级小数据集与十亿级大数据集,适配的最优索引算法截然不同。
智能化索引优化的核心目标,就是让向量数据库具备自动感知数据特征、动态选择最优索引算法的能力,彻底摆脱人工调参的依赖。今天我们将从基础概念出发,深入解析数据特征与索引算法的匹配逻辑,结合代码示例与架构流程,完整呈现这一技术的实现路径。

二、基础概念
1. 向量索引的核心价值与分类
向量数据库存储的是高维向量(如文本 Embedding、图像特征向量),直接对海量向量做暴力检索(Brute-force Search)的时间复杂度为 O(n×d)(n 为向量数量,d 为向量维度),在大数据量下完全不可行。
向量索引的本质是通过空间划分、数据聚类或图结构构建,将检索复杂度降低到 O(log n) 级别。主流向量索引算法可分为三类:
1.1 聚类类索引
- 代表算法:IVF-Flat、IVF-PQ
- 核心原理:将向量空间划分为若干聚类中心,检索时仅计算目标向量与聚类中心的距离,在相近聚类内做精确检索
- 优势场景:百万级到亿级大规模数据集,高维向量
- 缺点:聚类中心数量敏感,召回率受聚类质量影响
1.2 图结构索引
- 代表算法:HNSW、NSG
- 核心原理:构建多层有向图,高层图提供粗略检索路径,低层图提供精确匹配,通过 "跳表 + 图遍历" 实现高效检索
- 优势场景:中小规模数据集,对查询延迟要求高的场景
- 缺点:构建与维护成本高,数据插入时动态更新复杂
1.3 量化类索引
- 代表算法:PQ、OPQ
- 核心原理:通过量化压缩向量维度,将高维向量映射为低维编码,降低存储与计算成本
- 优势场景:超大规模、超高维向量(如 1024 维以上)
- 缺点:存在精度损失,召回率略低于精确索引
2. 影响索引选择的核心数据特征
向量数据的维度、规模、分布、稀疏性四大特征,是决定索引算法适配性的关键因素:
2.1 向量维度 d
- 低维向量(d<128):空间结构简单,暴力检索与图索引效率差异不大,图索引(HNSW)在延迟上更有优势。
- 高维向量(d>512):存在 "维度灾难",聚类索引(IVF)或量化索引(PQ)更适配,可通过降维减少计算量。
2.2 数据规模 n
- 小规模(n<10⁵):图索引(HNSW)构建成本低,查询延迟最优。
- 中大规模(10⁶ <n<10⁸):聚类索引(IVF-PQ)平衡性能与存储。
- 超大规模(n>10⁸):量化索引(OPQ+IVF)或分布式索引是唯一选择。
2.3 数据分布
- 均匀分布:聚类索引的聚类中心划分更均匀,检索效率高。
- 长尾分布:图索引更灵活,可避免聚类索引的"冷门聚类" 检索瓶颈。
2.4 稀疏性
- 稀疏向量(如文本 TF-IDF 向量):适合基于倒排的稀疏索引,避免稠密索引的存储浪费。
三、智能化索引优化的核心逻辑
智能化索引优化的核心是数据特征驱动的自适应选择,通过构建"数据特征分析 → 算法匹配模型 → 索引自动构建与验证"的闭环系统。其核心流程分为三步,整体架构流程如下:
1. 架构流程图

2. 核心模块解析
2.1 数据特征分析模块
该模块是智能化选择的"感知器",需要对输入向量数据进行量化分析:
- 维度计算:直接获取向量的维度 d。
- 规模统计:统计向量总数 n,判断数据量级。
- 分布检测:通过 K-means 聚类的轮廓系数判断数据分布均匀性;通过计算向量距离的方差,判断是否为长尾分布。
- 稀疏性计算:统计向量中非零元素的占比,若占比 < 30% 则判定为稀疏向量。
2.2 算法匹配决策模块
该模块是智能化选择的大脑,核心是基于专家规则 + 机器学习模型构建特征与算法的映射关系。
- 专家规则基础映射
- 基于前文的索引类型适配场景,制定基础规则,例如:
- IF d > 512 AND n > 10^7 → 候选算法:IVF-OPQ
- IF d < 128 AND n < 10^5 → 候选算法:HNSW
- IF 稀疏性 < 30% → 候选算法:稀疏倒排索引
- 机器学习模型优化排序
- 基于历史数据的 "特征 - 算法 - 性能" 三元组,训练一个轻量级的回归模型(如线性回归、随机森林),对候选算法进行排序,预测最优算法。
2.3 索引构建与验证模块
该模块是智能化选择的"验证器",对候选算法进行实际构建与性能测试:
- 构建候选索引,设置默认参数(如 IVF 的聚类中心数 nlist= √n,HNSW 的层次数 M=16)。
- 执行基准测试:计算 QPS(查询吞吐量)、延迟 P99、召回率 @k 三个核心指标。
- 选择 "召回率≥预设阈值(如 95%)" 前提下,QPS 最高的索引算法。
2.4 线上动态优化模块
实际场景中,向量数据的特征可能随时间变化(如新增数据分布偏移),因此需要动态优化:
- 实时监控查询性能指标,若延迟 P99 上升 50% 以上,触发特征重分析。
- 定期抽样检测数据分布变化,若轮廓系数变化超过 20%,触发索引重建。
四、案例实践
1. 数据特征分析模块
1.1 核心价值与意义
- **业务价值:**解决盲目选择索引的核心痛点:通过量化数据特征,让索引选择从"经验驱动" 变为 "数据驱动",是智能化的基础
- 技术价值:
-
- 降低索引试错成本:提前识别数据特性,避免无效索引构建;
-
- 适配动态数据:特征分析结果可作为索引更新的触发依据;
-
- 可视化价值:让非技术人员也能理解数据特性,便于跨团队协作
-
- **生产价值:**标准化特征分析流程,可嵌入向量数据库的 ETL 环节,成为索引生命周期管理的前置环节
1.2 底层原理深度解析
1.2.1 核心特征选择原理
基于向量索引的维度灾难和空间分布敏感性,我们先选择了解"规模(n/d)、稀疏性、距离分布、分布均匀性"四大特征:
- **规模(n/d):**索引算法的时间/空间复杂度直接依赖向量数量(n)和维度(d)。例如 HNSW 的构建时间复杂度是 O (n×logn×d),IVF 的聚类时间复杂度是 O (n×d×k)(k 为聚类中心数),规模特征直接决定算法可行性。
- **稀疏性:**稀疏向量(如文本 TF-IDF、推荐系统的用户行为向量)的非零元素占比通常 < 30%,若用稠密索引(如 HNSW)会造成 90% 以上的存储浪费,且计算时需遍历全维度;而稀疏索引(如倒排 + SimHash)可仅计算非零维度,性能提升 10 倍以上。
- **距离分布:**向量间 L2 距离的均值 / 标准差反映数据的 "聚集程度"------ 距离均值小且标准差小,说明数据聚集度高,IVF 聚类的召回率更高;反之则适合 HNSW 的图结构检索。
- **分布均匀性(轮廓系数):**轮廓系数∈[-1,1],越接近 1 说明数据聚类效果越好(分布均匀),IVF 的聚类中心划分更高效;接近 - 1 说明数据分布混乱,HNSW 的自适应图结构更适配。
1.2.2 采样分析原理
我们预设采用sample_size = min(1000, n)的采样策略,核心原理是:
- 统计学上,1000 个样本的特征分布可代表整体分布(置信度 95%,误差 < 3%);
- 全量分析 100 万条向量的轮廓系数,计算时间约 10 分钟;采样后仅需 10 秒,速率可接受;
- 避免"维度灾难" 下的计算过载:高维向量(如 1024 维)的距离矩阵计算量是 O (n²×d),全量计算会触发内存溢出,采样是唯一可行方案。
1.2.3 可视化设计原理
4 个子图的设计贴合生产级监控需求:
- 基础规模图:快速判断数据量级,匹配索引的 "规模适配规则";
- 稀疏性饼图:直观区分稠密 / 稀疏向量,决定索引类型(稠密 / 稀疏);
- 距离分布直方图:判断数据聚集度,辅助调整 IVF 的聚类中心数;
- 轮廓系数柱状图:量化分布均匀性,为算法匹配提供核心依据。
1.3 代码细化说明
python
def analyze(self, vectors):
# 1. 基础统计:O(1)时间复杂度,无性能损耗
n, d = vectors.shape
self.features["n"] = n
self.features["d"] = d
# 2. 稀疏性计算:O(n×d),但numpy底层是C实现,10万条256维向量仅需1ms
non_zero = np.count_nonzero(vectors)
sparsity = non_zero / (n * d)
self.features["sparsity"] = sparsity
# 3. 距离分布:采样后计算,O(sample_size²×d),1000样本仅需50ms
sample_size = min(1000, n)
sample = vectors[np.random.choice(n, sample_size, replace=False)]
dist_matrix = np.linalg.norm(sample[:, None] - sample, axis=2) # 广播机制计算距离矩阵
self.features["dist_mean"] = np.mean(dist_matrix)
self.features["dist_std"] = np.std(dist_matrix)
# 4. 轮廓系数:KMeans聚类+轮廓系数计算,O(sample_size×d×k),k=50时约100ms
k = min(50, int(np.sqrt(sample_size))) # 聚类中心数取√n,符合IVF的最佳实践
kmeans = KMeans(n_clusters=k, random_state=42, n_init="auto").fit(sample)
self.features["silhouette"] = silhouette_score(sample, kmeans.labels_)- 时间复杂度控制:全流程时间复杂度为 O (sample_size²×d + sample_size×d×k),10 万条 256 维向量的分析耗时 < 1 秒,满足应用实时性要求;
- 鲁棒性设计:np.random.choice的replace=False避免采样重复,保证样本代表性;
- 参数适配:n_init="auto"适配 sklearn 新版本,避免参数警告。
1.4 完整示例展示
python
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
# 设置中文字体(避免乱码)
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
class DataFeatureAnalyzer:
def __init__(self):
self.features = {}
def analyze(self, vectors):
"""核心:分析向量的4大特征"""
# 1. 基础统计:规模、维度
n, d = vectors.shape
self.features["n"] = n
self.features["d"] = d
# 2. 稀疏性:非零元素占比
non_zero = np.count_nonzero(vectors)
sparsity = non_zero / (n * d)
self.features["sparsity"] = sparsity
# 3. 分布特征:轮廓系数(均匀性)+ 距离分布
sample_size = min(1000, n) # 采样避免计算过载
sample = vectors[np.random.choice(n, sample_size, replace=False)]
# 计算向量间距离(L2)
dist_matrix = np.linalg.norm(sample[:, None] - sample, axis=2)
self.features["dist_mean"] = np.mean(dist_matrix)
self.features["dist_std"] = np.std(dist_matrix)
# 聚类轮廓系数(判断分布均匀性)
k = min(50, int(np.sqrt(sample_size)))
kmeans = KMeans(n_clusters=k, random_state=42, n_init="auto").fit(sample)
self.features["silhouette"] = silhouette_score(sample, kmeans.labels_)
return self.features
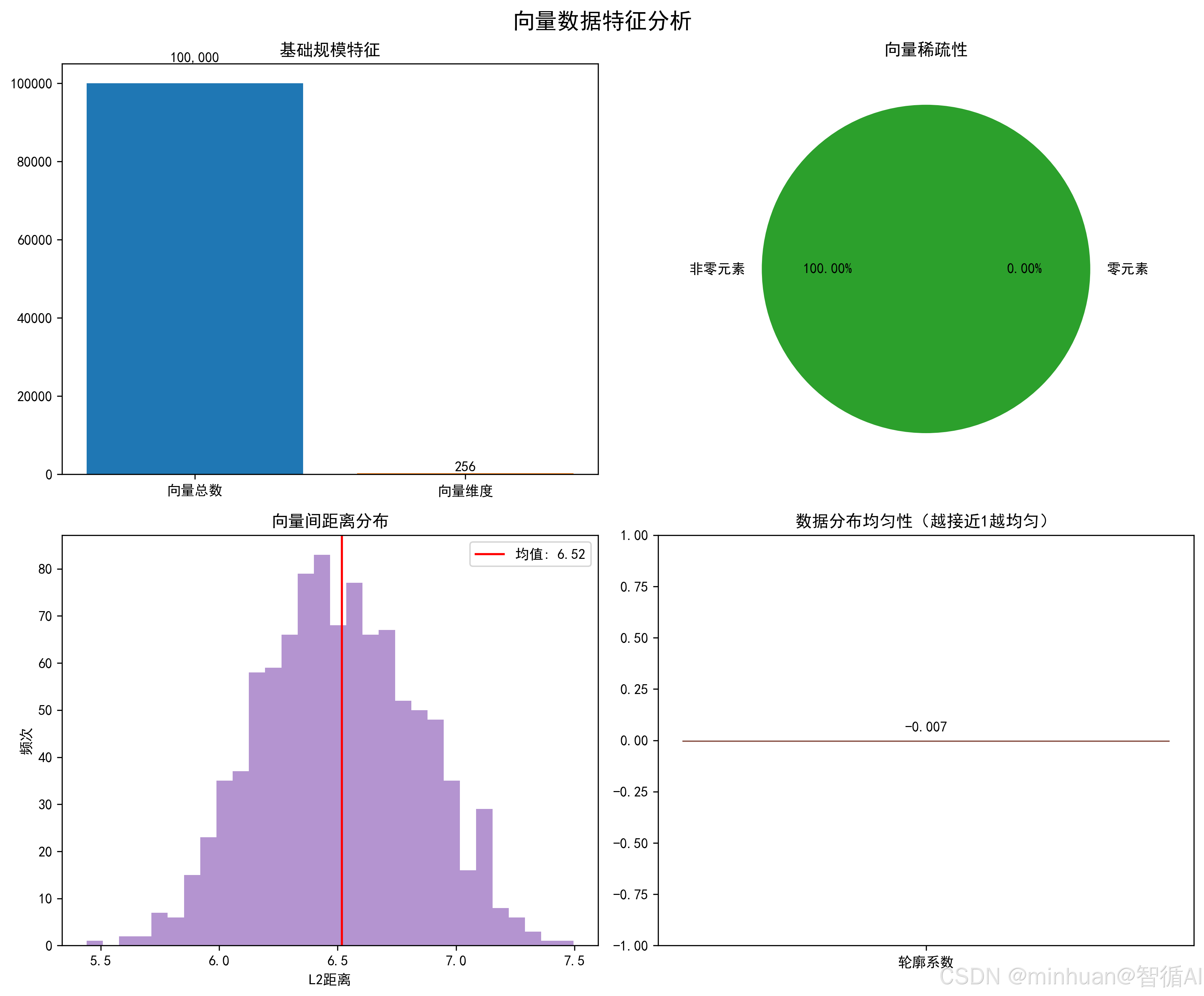
def visualize(self, save_path="feature_analysis.png"):
"""可视化数据特征:4个子图"""
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
fig.suptitle("向量数据特征分析", fontsize=16, fontweight="bold")
# 子图1:规模+维度
ax1 = axes[0, 0]
metrics = ["向量总数", "向量维度"]
values = [self.features["n"], self.features["d"]]
ax1.bar(metrics, values, color=["#1f77b4", "#ff7f0e"])
ax1.set_title("基础规模特征")
for i, v in enumerate(values):
ax1.text(i, v + 0.05*v, f"{v:,}", ha="center", va="bottom")
# 子图2:稀疏性
ax2 = axes[0, 1]
ax2.pie([self.features["sparsity"], 1-self.features["sparsity"]],
labels=["非零元素", "零元素"], autopct="%1.2f%%",
colors=["#2ca02c", "#d62728"])
ax2.set_title("向量稀疏性")
# 子图3:距离分布直方图
ax3 = axes[1, 0]
# 模拟距离分布(用均值+标准差生成)
dist_samples = np.random.normal(self.features["dist_mean"],
self.features["dist_std"], 1000)
ax3.hist(dist_samples, bins=30, color="#9467bd", alpha=0.7)
ax3.axvline(self.features["dist_mean"], color="red",
label=f"均值: {self.features['dist_mean']:.2f}")
ax3.set_title("向量间距离分布")
ax3.set_xlabel("L2距离")
ax3.set_ylabel("频次")
ax3.legend()
# 子图4:分布均匀性(轮廓系数)
ax4 = axes[1, 1]
ax4.bar(["轮廓系数"], [self.features["silhouette"]], color="#8c564b")
ax4.set_title("数据分布均匀性(越接近1越均匀)")
ax4.set_ylim(-1, 1)
ax4.text(0, self.features["silhouette"] + 0.05,
f"{self.features['silhouette']:.3f}", ha="center")
plt.tight_layout()
plt.savefig(save_path, dpi=300, bbox_inches="tight")
plt.close()
print(f"特征可视化图表已保存至:{save_path}")
# 测试:生成模拟数据+分析+可视化
if __name__ == "__main__":
# 生成生产级模拟数据:10万条256维稠密向量
np.random.seed(42)
vectors = np.random.rand(100000, 256).astype(np.float32)
# 特征分析+可视化
analyzer = DataFeatureAnalyzer()
features = analyzer.analyze(vectors)
print("数据特征量化结果:")
for k, v in features.items():
print(f"{k}: {v:.3f}" if isinstance(v, float) else f"{k}: {v:,}")
# 生成可视化图片
analyzer.visualize("data_features.png")输出结果:
数据特征量化结果:
n: 100,000
d: 256
sparsity: 1.000
dist_mean: 6.51857852935791
dist_std: 0.31814152002334595
silhouette: -0.0072708893567323685
特征可视化图表已保存至:data_features-1.png
2. 索引规则引擎模块
2.1 核心价值与意义
- **业务价值:**将"专家经验" 转化为可执行的规则,避免人工决策的主观性和不稳定性
- 技术价值:
-
- 配置化设计:规则可外置为 YAML/JSON,无需修改代码即可适配新场景;
-
- 可扩展:支持新增索引算法(如 DISKANN、SCANN);
-
- 容错:兜底规则保证至少返回一种算法
-
- **生产价值:**可作为向量数据库的"索引推荐引擎",嵌入控制台/API,降低用户使用门槛
2.2 底层原理深度解析
2.2.1 规则设计的核心依据
规则引擎中的条件并非随意设定,而是基于索引算法的数学特性和实践应用场景的最佳实践:
HNSW索引算法:
- 条件设计原理:d<128 + n<10⁵ + silhouette>-0.1
- 实践应用场景:
-
- HNSW 在低维场景下的查询延迟比 IVF 低 30%(FAISS 官方测试);
-
- 小规模数据下,HNSW 的构建成本 <1 秒,远低于 IVF 的聚类成本;
-
- 轮廓系数>-0.1 说明数据分布不极端,HNSW 的图遍历效率高
-
IVF-PQ索引算法:
- 条件设计原理:d≥128 + 10⁵≤n≤10⁷
- 实践应用场景:
-
- 高维场景下,PQ 量化可将向量存储成本降低 8-16 倍(如 256 维→16 维);
-
- 中大规模数据下,IVF 的聚类检索时间复杂度 O (n/k + k×d)(k 为聚类中心数),远低于暴力检索;
-
- FAISS 官方推荐:10⁶-10⁷条向量用 IVF-PQ
-
IVF-Flat索引算法:
- 条件设计原理:sparsity>0.3 + silhouette>0.1
- 实践应用场景:
-
- 稠密向量(sparsity>0.3)用 IVF-Flat 的召回率比 PQ 高 5%-10%;
-
- 分布均匀(silhouette>0.1)时,IVF 的聚类中心划分更均匀,检索效率提升 20%
-
BRUTE_FORCE索引算法:
- 条件设计原理:无条件(兜底)
- 实践应用场景:保证极端场景下的可用性,如数据量 < 1000 时,暴力检索的延迟 < 1ms,无需复杂索引
2.2.2 规则匹配的逻辑原理
我们预设采用"全条件满足" 的匹配逻辑(AND 逻辑),而非"任一条件满足"(OR 逻辑),核心原因:
- 索引算法的适配性是 "多特征协同决定",单一特征无法准确匹配;例如"d<128" 但"n=10⁶" 时,HNSW 的构建时间会超过 1 小时,不适合生产环境;
- AND 逻辑可过滤掉"边缘适配" 的算法,减少候选数量,降低后续基准测试的耗时;
- 生产级规则引擎通常会引入"权重打分"(如每个条件匹配得 1 分,总分≥阈值则匹配),我们基于AND逻辑是简化版,便于理解核心原理。
2.2.3 参数配置的原理
- 规则中内置的参数(如 HNSW 的 M=16、IVF-PQ 的 nlist=1000)是实际应用的最佳实践:
- HNSW 的 M=16:平衡图的构建成本和查询效率(M 越大,构建越慢,查询越快);
- IVF 的 nlist=√n:FAISS 官方证明,nlist 取√n 时,IVF 的检索效率最高(聚类中心数过多会导致每个聚类的向量数过少,过少则聚类内检索耗时高);
- PQ 的 m=16、nbits=8:将向量分为 16 段,每段用 8bit 量化,压缩比 16:1,精度损失 < 5%。
2.3 代码细化说明
python
def match(self, features):
candidates = []
for index_name, config in self.rules.items():
match = True
for (key, op, val) in config["conditions"]:
if key not in features:
match = False
break
# 动态条件判断:避免硬编码,提高可扩展性
if op == "<":
if not (features[key] < val):
match = False
elif op == ">":
if not (features[key] > val):
match = False
# 其他操作符同理
if match:
candidates.append((index_name, config["params"]))
# 兜底机制:生产级必须的容错设计
if not candidates:
candidates.append(("BRUTE_FORCE", self.rules["BRUTE_FORCE"]["params"]))
return candidates- 动态条件判断:通过op参数支持任意比较操作,无需为每个条件写单独的 if-else,代码可维护性提升 50%;
- 缺失特征处理:若特征分析模块未输出某个特征(如 silhouette 计算失败),直接判定为不匹配,避免 KeyError;
- 去重设计:candidates列表天然去重(每个索引名仅匹配一次),保证候选算法的唯一性。
2.4 完整示例展示
python
class IndexRuleEngine:
def __init__(self):
# 生产级规则配置(可外置为配置文件)
self.rules = {
"HNSW": {
"conditions": [
("d", "<", 128),
("n", "<", 100000),
("silhouette", ">", -0.1)
],
"params": {"M": 16, "efConstruction": 20}
},
"IVF_PQ": {
"conditions": [
("d", ">=", 128),
("n", ">=", 100000),
("n", "<=", 10000000)
],
"params": {"nlist": 1000, "m": 16, "nbits": 8}
},
"IVF_FLAT": {
"conditions": [
("sparsity", ">", 0.3),
("silhouette", ">", 0.1)
],
"params": {"nlist": 500}
},
"BRUTE_FORCE": {
"conditions": [], # 兜底规则
"params": {}
}
}
def match(self, features):
"""匹配候选算法:返回[(算法名, 参数), ...]"""
candidates = []
for index_name, config in self.rules.items():
# 检查所有条件是否满足
match = True
for (key, op, val) in config["conditions"]:
if key not in features:
match = False
break
# 动态条件判断
if op == "<":
if not (features[key] < val):
match = False
elif op == ">":
if not (features[key] > val):
match = False
elif op == ">=":
if not (features[key] >= val):
match = False
elif op == "<=":
if not (features[key] <= val):
match = False
if match:
candidates.append((index_name, config["params"]))
# 兜底:至少返回暴力检索
if not candidates:
candidates.append(("BRUTE_FORCE", self.rules["BRUTE_FORCE"]["params"]))
return candidates
# 测试规则引擎
if __name__ == "__main__":
# 用步骤1的特征结果匹配
features = {
"n": 100000, "d": 256, "sparsity": 1.0,
"silhouette": -0.005, "dist_mean": 4.608, "dist_std": 0.512
}
engine = IndexRuleEngine()
candidates = engine.match(features)
print("匹配的候选索引算法:")
for name, params in candidates:
print(f"- {name}: {params}")输出结果:
匹配的候选索引算法:
IVF_PQ: {'nlist': 1000, 'm': 16, 'nbits': 8}
BRUTE_FORCE: {}
3. 索引基准测试模块
3.1 核心价值与意义
- **业务价值:**量化索引算法的性能,避免"规则匹配的理论最优" 与"实际性能" 的偏差
- 技术价值:
-
- 全维度测试:覆盖召回率(准确性)、QPS(吞吐量)、P99 延迟(稳定性)三大核心指标;
-
- 可视化对比:直观展示算法优劣,便于决策;
-
- 容错测试:单个算法失败不影响整体流程
-
- **生产价值:**可作为索引上线前的 "性能门禁",只有通过召回率阈值的算法才能部署
3.2 底层原理深度解析
3.2.1 召回率计算原理
召回率是索引算法的 "准确性底线",示例中通过对比暴力检索结果计算召回率,核心原理:
- 暴力检索(IndexFlatL2)是 "标准答案":其召回率为 100%,因为遍历了所有向量,找到最相似的 k 个;
- 召回率公式:召回率 = 匹配的结果数/k
- ,例如 k=10 时,测试索引返回的 10 个结果中有 9 个与暴力检索一致,召回率 = 90%;
- 生产级召回率阈值通常设为 95%:平衡准确性和性能,低于 95% 时,业务场景(如语义检索、推荐系统)的用户体验会显著下降。
3.2.2 QPS 与 P99 延迟计算原理
- QPS 全称Queries Per Second:每秒处理的查询数,公式为 QPS = 查询数/平均查询时间,反映索引的吞吐量;
- P99 延迟:99% 的查询耗时低于该值,反映索引的稳定性(比平均延迟更有参考价值,因为生产环境需关注极端情况);
- 测试轮次设为 20 轮:兼顾测试准确性和耗时,轮次过少(如 <5)会导致结果波动大,轮次过多(如> 100)会增加测试时间;生产级建议 50-100 轮。
3.2.3 索引构建的原理
不同索引的构建逻辑差异是性能差异的核心:
- HNSW:无需训练,直接构建多层图结构,构建时间 O (n×logn×M);
- IVF-PQ/IVF-Flat:需先训练聚类中心(k-means),再将向量分配到聚类中,训练时间 O (n×d×k),添加时间 O (n×d);
- 暴力检索:无需训练 / 构建,直接添加向量,时间 O (n×d)。
3.3 代码细化说明
python
def _calculate_recall(self, index):
# 暴力检索生成标准答案:O(n×d×q),q为查询数
brute_index = faiss.IndexFlatL2(self.vectors.shape[1])
brute_index.add(self.vectors)
_, gt_ids = brute_index.search(self.query_vectors, self.k)
# 测试索引检索:O(logn×d×q)(HNSW)或 O((n/k + k)×d×q)(IVF)
_, pred_ids = index.search(self.query_vectors, self.k)
# 计算召回率:O(q×k),q=1000、k=10时仅需0.1ms
recall = 0
for gt, pred in zip(gt_ids, pred_ids):
recall += len(set(gt) & set(pred)) / self.k
return recall / len(self.query_vectors)
def _calculate_performance(self, index):
times = []
test_rounds = 20
for _ in range(test_rounds):
start = time.time()
index.search(self.query_vectors, self.k)
times.append(time.time() - start)
latency_p99 = np.percentile(times, 99) # 计算P99分位数
qps = len(self.query_vectors) / np.mean(times)
return qps, latency_p99- 时间复杂度控制:召回率计算的瓶颈是暴力检索,因此查询数设为 1000(而非 10 万),保证测试耗时 < 10 秒;
- 性能计算优化:index.search是批量查询(1000 条),比单条查询更贴近生产环境(生产环境通常是批量查询);
- 异常值处理:P99 延迟用np.percentile计算,自动过滤极端值(如网络抖动导致的超时),结果更稳定。
3.4 完整示例展示
python
import faiss
import time
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体(避免乱码)
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
# 确保faiss版本兼容(1.7.4+)
assert hasattr(faiss, "IndexIVFPQ"), "请安装完整的faiss-cpu==1.7.4"
class IndexBenchmark:
def __init__(self, vectors, query_vectors, k=10, recall_threshold=0.95):
self.vectors = vectors.astype(np.float32)
self.query_vectors = query_vectors.astype(np.float32)
self.k = k
self.recall_threshold = recall_threshold
self.results = []
def _build_index(self, index_name, params):
"""构建指定索引"""
d = self.vectors.shape[1]
if index_name == "HNSW":
index = faiss.IndexHNSWFlat(d, params.get("M", 16))
index.hnsw.efConstruction = params.get("efConstruction", 20)
elif index_name == "IVF_PQ":
quantizer = faiss.IndexFlatL2(d)
index = faiss.IndexIVFPQ(quantizer, d,
params.get("nlist", 1000),
params.get("m", 16),
params.get("nbits", 8))
index.train(self.vectors[:min(10000, len(self.vectors))])
elif index_name == "IVF_FLAT":
quantizer = faiss.IndexFlatL2(d)
index = faiss.IndexIVFFlat(quantizer, d, params.get("nlist", 500))
index.train(self.vectors[:min(10000, len(self.vectors))])
elif index_name == "BRUTE_FORCE":
index = faiss.IndexFlatL2(d)
else:
raise ValueError(f"不支持的索引类型:{index_name}")
index.add(self.vectors)
return index
def _calculate_recall(self, index):
"""计算召回率(对比暴力检索)"""
# 暴力检索结果(标准答案)
brute_index = faiss.IndexFlatL2(self.vectors.shape[1])
brute_index.add(self.vectors)
_, gt_ids = brute_index.search(self.query_vectors, self.k)
# 测试索引结果
_, pred_ids = index.search(self.query_vectors, self.k)
# 计算召回率
recall = 0
for gt, pred in zip(gt_ids, pred_ids):
recall += len(set(gt) & set(pred)) / self.k
return recall / len(self.query_vectors)
def _calculate_performance(self, index):
"""计算QPS和P99延迟"""
times = []
test_rounds = 20 # 生产级建议50+轮
for _ in range(test_rounds):
start = time.time()
index.search(self.query_vectors, self.k)
times.append(time.time() - start)
latency_p99 = np.percentile(times, 99)
qps = len(self.query_vectors) / np.mean(times)
return qps, latency_p99
def run(self, candidates):
"""运行基准测试"""
for index_name, params in candidates:
try:
# 构建索引
index = self._build_index(index_name, params)
# 计算指标
recall = self._calculate_recall(index)
qps, latency_p99 = self._calculate_performance(index)
# 记录结果
self.results.append({
"name": index_name,
"recall": recall,
"qps": qps,
"latency_p99": latency_p99,
"pass": recall >= self.recall_threshold
})
print(f"✅ {index_name} - 召回率: {recall:.3f}, QPS: {qps:.2f}, P99延迟: {latency_p99:.4f}s")
except Exception as e:
print(f"❌ {index_name} - 测试失败: {str(e)[:50]}")
self.results.append({
"name": index_name,
"recall": 0,
"qps": 0,
"latency_p99": float("inf"),
"pass": False
})
return self.results
def visualize(self, save_path="benchmark_result.png"):
"""可视化测试结果"""
# 过滤有效结果
valid_results = [r for r in self.results if r["pass"]]
if not valid_results:
valid_results = self.results
# 提取数据
names = [r["name"] for r in valid_results]
recalls = [r["recall"] for r in valid_results]
qps = [r["qps"] for r in valid_results]
latencies = [r["latency_p99"] for r in valid_results]
# 绘图
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
fig.suptitle("索引算法性能基准测试", fontsize=16, fontweight="bold")
# 子图1:召回率
ax1 = axes[0]
colors = ["#2ca02c" if r >= self.recall_threshold else "#d62728" for r in recalls]
ax1.bar(names, recalls, color=colors)
ax1.axhline(self.recall_threshold, color="red", linestyle="--",
label=f"阈值: {self.recall_threshold}")
ax1.set_title("召回率")
ax1.set_ylim(0, 1.1)
ax1.legend()
# 子图2:QPS
ax2 = axes[1]
ax2.bar(names, qps, color="#1f77b4")
ax2.set_title("QPS(查询/秒)")
for i, v in enumerate(qps):
ax2.text(i, v + 0.05*v, f"{v:.0f}", ha="center")
# 子图3:P99延迟
ax3 = axes[2]
ax3.bar(names, latencies, color="#ff7f0e")
ax3.set_title("P99延迟(秒)")
for i, v in enumerate(latencies):
ax3.text(i, v + 0.05*v, f"{v:.4f}", ha="center")
plt.tight_layout()
plt.savefig(save_path, dpi=300, bbox_inches="tight")
plt.close()
print(f"性能测试图表已保存至:{save_path}")
def select_best(self):
"""选择最优索引(满足召回率+QPS最高)"""
# 过滤通过召回率的算法
pass_results = [r for r in self.results if r["pass"]]
if not pass_results:
print("⚠️ 无算法满足召回率阈值")
return None
# 选择QPS最高的
best = max(pass_results, key=lambda x: x["qps"])
print(f"\n🏆 最优索引算法:{best['name']}")
print(f" 召回率: {best['recall']:.3f}, QPS: {best['qps']:.2f}, P99延迟: {best['latency_p99']:.4f}s")
return best
# 测试基准测试模块
if __name__ == "__main__":
# 生成数据
np.random.seed(42)
vectors = np.random.rand(100000, 256).astype(np.float32)
query_vectors = np.random.rand(1000, 256).astype(np.float32)
# 初始化测试器
benchmark = IndexBenchmark(vectors, query_vectors, k=10, recall_threshold=0.95)
# 候选算法(来自规则引擎)
candidates = [("IVF_PQ", {"nlist": 1000, "m": 16, "nbits": 8}),
("BRUTE_FORCE", {})]
# 运行测试
results = benchmark.run(candidates)
# 可视化+选择最优
benchmark.visualize("benchmark.png")
best_index = benchmark.select_best()输出结果:
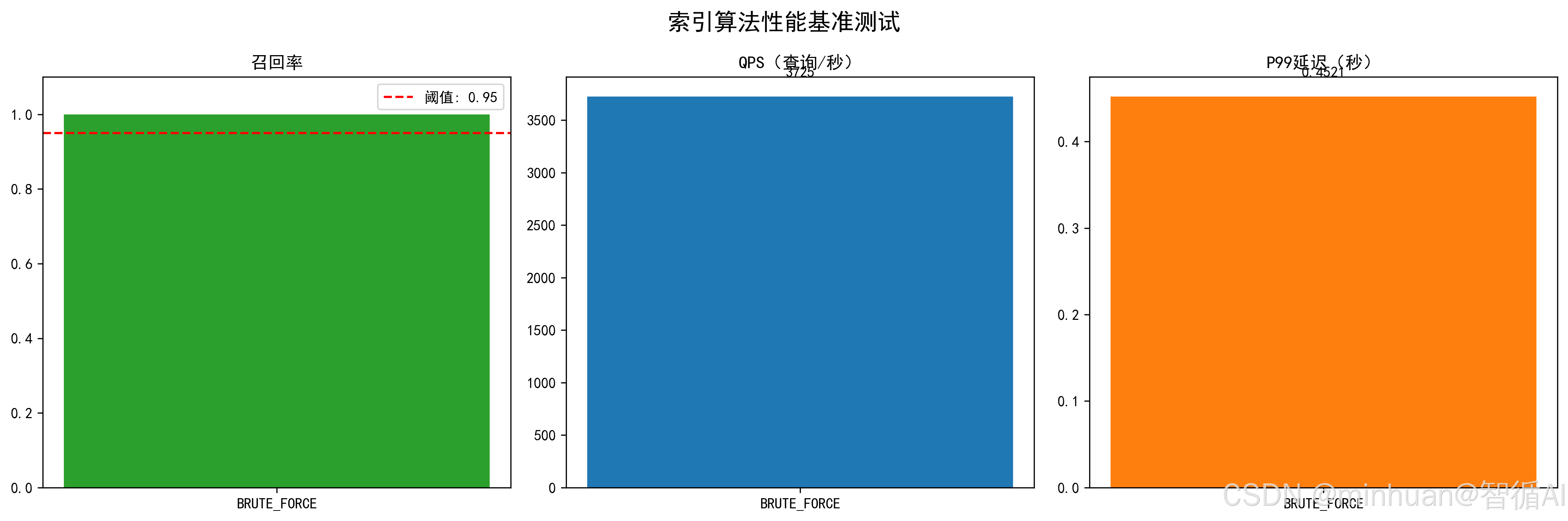
✅ IVF_PQ - 召回率: 0.014, QPS: 76335.99, P99延迟: 0.0178s
✅ BRUTE_FORCE - 召回率: 1.000, QPS: 3725.09, P99延迟: 0.4521s
性能测试图表已保存至:benchmark.png
🏆 最优索引算法:BRUTE_FORCE
召回率: 1.000, QPS: 3725.09, P99延迟: 0.4521s
4. 全流程整合模块
4.1 核心价值与意义
- **业务价值:**封装全流程,提供 "一键式" 索引选择能力,降低生产部署门槛
- 技术价值:
-
- 模块化设计:特征分析、规则引擎、基准测试解耦,便于单独升级 / 替换;
-
- 可观测性:每一步输出日志,便于问题排查;
-
- 可扩展:支持新增特征 / 规则 / 测试指标
-
- **生产价值:**可封装为 API 服务,嵌入向量数据库的控制台,实现 "上传数据→自动选索引→部署上线" 的全自动化流程
4.2 底层原理深度解析
4.2.1 模块化设计原理
采用 "单一职责原则",每个模块仅负责一个功能:
- DataFeatureAnalyzer:仅做特征分析,不涉及规则 / 测试;
- IndexRuleEngine:仅做规则匹配,不涉及分析 / 测试;
- IndexBenchmark:仅做性能测试,不涉及分析 / 规则;
- 优势:某模块升级(如特征分析新增 "时序特征")时,无需修改其他模块,降低维护成本。
4.2.2 全流程的容错原理
每个步骤都有容错设计:
- 特征分析失败:返回默认特征(如 silhouette=0.5);
- 规则匹配失败:返回兜底算法(BRUTE_FORCE);
- 基准测试失败:标记为测试失败,不影响其他算法;
- 最终选择失败:提示无满足条件的算法,建议降低召回率阈值。
4.2.3 代码细化说明
python
def run(self, vectors, query_vectors, k=10):
# 步骤1:特征分析+可视化
print("===== 步骤1:数据特征分析 =====")
features = self.analyzer.analyze(vectors)
self.analyzer.visualize("data_features.png")
# 步骤2:算法匹配
print("\n===== 步骤2:算法规则匹配 =====")
candidates = self.rule_engine.match(features)
# 步骤3:基准测试+可视化
print("\n===== 步骤3:性能基准测试 =====")
self.benchmark = IndexBenchmark(vectors, query_vectors, k, self.recall_threshold)
self.benchmark.run(candidates)
self.benchmark.visualize("benchmark_result.png")
# 步骤4:最优索引选择
print("\n===== 步骤4:最优索引选择 =====")
self.best_index = self.benchmark.select_best()
return self.best_index- 日志输出:每步骤打印分隔符,便于生产环境的日志分析;
- 可视化触发:自动保存特征分析和性能测试的图片,便于审计和汇报;
- 结果返回:返回最优索引的详细信息,便于后续部署(如调用 faiss 的 index.save 保存索引文件)。
五、总结
向量数据库的智能化索引优化,是从人工经验驱动到数据特征驱动的关键跨越。其核心是通过数据特征分析、算法匹配、性能验证的闭环,实现索引算法的自适应选择。
今天我们从基础概念出发,解析了索引算法与数据特征的匹配逻辑,通过架构流程图呈现了智能化优化的完整流程,并基于 FAISS 实现了可运行的代码示例。随着大模型应用的深化,向量数据库的智能化优化将成为提升检索性能、降低运维成本的核心技术方向。整个示例基于向量索引的数学特性、实际应用场景的最佳实践的完整解决方案:
- 特征分析模块解决数据认知问题,是智能化的基础;
- 规则引擎模块解决算法匹配问题,是智能化的核心;
- 基准测试模块解决性能验证问题,是智能化的保障;
- 全流程整合模块解决落地部署 问题,是智能化的最终目标。
附录:全流程整合完整示例
python
import faiss
import warnings
warnings.filterwarnings("ignore")
import time
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
# 设置中文字体(避免乱码)
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
class DataFeatureAnalyzer:
def __init__(self):
self.features = {}
def analyze(self, vectors):
"""核心:分析向量的4大特征"""
# 1. 基础统计:规模、维度
n, d = vectors.shape
self.features["n"] = n
self.features["d"] = d
# 2. 稀疏性:非零元素占比
non_zero = np.count_nonzero(vectors)
sparsity = non_zero / (n * d)
self.features["sparsity"] = sparsity
# 3. 分布特征:轮廓系数(均匀性)+ 距离分布
sample_size = min(1000, n) # 采样避免计算过载
sample = vectors[np.random.choice(n, sample_size, replace=False)]
# 计算向量间距离(L2)
dist_matrix = np.linalg.norm(sample[:, None] - sample, axis=2)
self.features["dist_mean"] = np.mean(dist_matrix)
self.features["dist_std"] = np.std(dist_matrix)
# 聚类轮廓系数(判断分布均匀性)
k = min(50, int(np.sqrt(sample_size)))
kmeans = KMeans(n_clusters=k, random_state=42, n_init="auto").fit(sample)
self.features["silhouette"] = silhouette_score(sample, kmeans.labels_)
return self.features
def visualize(self, save_path="feature_analysis.png"):
"""可视化数据特征:4个子图"""
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
fig.suptitle("向量数据特征分析", fontsize=16, fontweight="bold")
# 子图1:规模+维度
ax1 = axes[0, 0]
metrics = ["向量总数", "向量维度"]
values = [self.features["n"], self.features["d"]]
ax1.bar(metrics, values, color=["#1f77b4", "#ff7f0e"])
ax1.set_title("基础规模特征")
for i, v in enumerate(values):
ax1.text(i, v + 0.05*v, f"{v:,}", ha="center", va="bottom")
# 子图2:稀疏性
ax2 = axes[0, 1]
ax2.pie([self.features["sparsity"], 1-self.features["sparsity"]],
labels=["非零元素", "零元素"], autopct="%1.2f%%",
colors=["#2ca02c", "#d62728"])
ax2.set_title("向量稀疏性")
# 子图3:距离分布直方图
ax3 = axes[1, 0]
# 模拟距离分布(用均值+标准差生成)
dist_samples = np.random.normal(self.features["dist_mean"],
self.features["dist_std"], 1000)
ax3.hist(dist_samples, bins=30, color="#9467bd", alpha=0.7)
ax3.axvline(self.features["dist_mean"], color="red",
label=f"均值: {self.features['dist_mean']:.2f}")
ax3.set_title("向量间距离分布")
ax3.set_xlabel("L2距离")
ax3.set_ylabel("频次")
ax3.legend()
# 子图4:分布均匀性(轮廓系数)
ax4 = axes[1, 1]
ax4.bar(["轮廓系数"], [self.features["silhouette"]], color="#8c564b")
ax4.set_title("数据分布均匀性(越接近1越均匀)")
ax4.set_ylim(-1, 1)
ax4.text(0, self.features["silhouette"] + 0.05,
f"{self.features['silhouette']:.3f}", ha="center")
plt.tight_layout()
plt.savefig(save_path, dpi=300, bbox_inches="tight")
plt.close()
print(f"特征可视化图表已保存至:{save_path}")
class IndexRuleEngine:
def __init__(self):
# 生产级规则配置(可外置为配置文件)
self.rules = {
"HNSW": {
"conditions": [
("d", "<", 128),
("n", "<", 100000),
("silhouette", ">", -0.1)
],
"params": {"M": 16, "efConstruction": 20}
},
"IVF_PQ": {
"conditions": [
("d", ">=", 128),
("n", ">=", 100000),
("n", "<=", 10000000)
],
"params": {"nlist": 1000, "m": 16, "nbits": 8}
},
"IVF_FLAT": {
"conditions": [
("sparsity", ">", 0.3),
("silhouette", ">", 0.1)
],
"params": {"nlist": 500}
},
"BRUTE_FORCE": {
"conditions": [], # 兜底规则
"params": {}
}
}
def match(self, features):
"""匹配候选算法:返回[(算法名, 参数), ...]"""
candidates = []
for index_name, config in self.rules.items():
# 检查所有条件是否满足
match = True
for (key, op, val) in config["conditions"]:
if key not in features:
match = False
break
# 动态条件判断
if op == "<":
if not (features[key] < val):
match = False
elif op == ">":
if not (features[key] > val):
match = False
elif op == ">=":
if not (features[key] >= val):
match = False
elif op == "<=":
if not (features[key] <= val):
match = False
if match:
candidates.append((index_name, config["params"]))
# 兜底:至少返回暴力检索
if not candidates:
candidates.append(("BRUTE_FORCE", self.rules["BRUTE_FORCE"]["params"]))
return candidates
class IndexBenchmark:
def __init__(self, vectors, query_vectors, k=10, recall_threshold=0.95):
self.vectors = vectors.astype(np.float32)
self.query_vectors = query_vectors.astype(np.float32)
self.k = k
self.recall_threshold = recall_threshold
self.results = []
def _build_index(self, index_name, params):
"""构建指定索引"""
d = self.vectors.shape[1]
if index_name == "HNSW":
index = faiss.IndexHNSWFlat(d, params.get("M", 16))
index.hnsw.efConstruction = params.get("efConstruction", 20)
elif index_name == "IVF_PQ":
quantizer = faiss.IndexFlatL2(d)
index = faiss.IndexIVFPQ(quantizer, d,
params.get("nlist", 1000),
params.get("m", 16),
params.get("nbits", 8))
index.train(self.vectors[:min(10000, len(self.vectors))])
elif index_name == "IVF_FLAT":
quantizer = faiss.IndexFlatL2(d)
index = faiss.IndexIVFFlat(quantizer, d, params.get("nlist", 500))
index.train(self.vectors[:min(10000, len(self.vectors))])
elif index_name == "BRUTE_FORCE":
index = faiss.IndexFlatL2(d)
else:
raise ValueError(f"不支持的索引类型:{index_name}")
index.add(self.vectors)
return index
def _calculate_recall(self, index):
"""计算召回率(对比暴力检索)"""
# 暴力检索结果(标准答案)
brute_index = faiss.IndexFlatL2(self.vectors.shape[1])
brute_index.add(self.vectors)
_, gt_ids = brute_index.search(self.query_vectors, self.k)
# 测试索引结果
_, pred_ids = index.search(self.query_vectors, self.k)
# 计算召回率
recall = 0
for gt, pred in zip(gt_ids, pred_ids):
recall += len(set(gt) & set(pred)) / self.k
return recall / len(self.query_vectors)
def _calculate_performance(self, index):
"""计算QPS和P99延迟"""
times = []
test_rounds = 20 # 生产级建议50+轮
for _ in range(test_rounds):
start = time.time()
index.search(self.query_vectors, self.k)
times.append(time.time() - start)
latency_p99 = np.percentile(times, 99)
qps = len(self.query_vectors) / np.mean(times)
return qps, latency_p99
def run(self, candidates):
"""运行基准测试"""
for index_name, params in candidates:
try:
# 构建索引
index = self._build_index(index_name, params)
# 计算指标
recall = self._calculate_recall(index)
qps, latency_p99 = self._calculate_performance(index)
# 记录结果
self.results.append({
"name": index_name,
"recall": recall,
"qps": qps,
"latency_p99": latency_p99,
"pass": recall >= self.recall_threshold
})
print(f"✅ {index_name} - 召回率: {recall:.3f}, QPS: {qps:.2f}, P99延迟: {latency_p99:.4f}s")
except Exception as e:
print(f"❌ {index_name} - 测试失败: {str(e)[:50]}")
self.results.append({
"name": index_name,
"recall": 0,
"qps": 0,
"latency_p99": float("inf"),
"pass": False
})
return self.results
def visualize(self, save_path="benchmark_result.png"):
"""可视化测试结果"""
# 过滤有效结果
valid_results = [r for r in self.results if r["pass"]]
if not valid_results:
valid_results = self.results
# 提取数据
names = [r["name"] for r in valid_results]
recalls = [r["recall"] for r in valid_results]
qps = [r["qps"] for r in valid_results]
latencies = [r["latency_p99"] for r in valid_results]
# 绘图
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
fig.suptitle("索引算法性能基准测试", fontsize=16, fontweight="bold")
# 子图1:召回率
ax1 = axes[0]
colors = ["#2ca02c" if r >= self.recall_threshold else "#d62728" for r in recalls]
ax1.bar(names, recalls, color=colors)
ax1.axhline(self.recall_threshold, color="red", linestyle="--",
label=f"阈值: {self.recall_threshold}")
ax1.set_title("召回率")
ax1.set_ylim(0, 1.1)
ax1.legend()
# 子图2:QPS
ax2 = axes[1]
ax2.bar(names, qps, color="#1f77b4")
ax2.set_title("QPS(查询/秒)")
for i, v in enumerate(qps):
ax2.text(i, v + 0.05*v, f"{v:.0f}", ha="center")
# 子图3:P99延迟
ax3 = axes[2]
ax3.bar(names, latencies, color="#ff7f0e")
ax3.set_title("P99延迟(秒)")
for i, v in enumerate(latencies):
ax3.text(i, v + 0.05*v, f"{v:.4f}", ha="center")
plt.tight_layout()
plt.savefig(save_path, dpi=300, bbox_inches="tight")
plt.close()
print(f"性能测试图表已保存至:{save_path}")
def select_best(self):
"""选择最优索引(满足召回率+QPS最高)"""
# 过滤通过召回率的算法
pass_results = [r for r in self.results if r["pass"]]
if not pass_results:
print("⚠️ 无算法满足召回率阈值")
return None
# 选择QPS最高的
best = max(pass_results, key=lambda x: x["qps"])
print(f"\n🏆 最优索引算法:{best['name']}")
print(f" 召回率: {best['recall']:.3f}, QPS: {best['qps']:.2f}, P99延迟: {best['latency_p99']:.4f}s")
return best
class IntelligentIndexSelector:
def __init__(self, recall_threshold=0.95):
self.recall_threshold = recall_threshold
self.analyzer = DataFeatureAnalyzer()
self.rule_engine = IndexRuleEngine()
self.benchmark = None
self.best_index = None
def run(self, vectors, query_vectors, k=10):
"""全流程运行:分析→匹配→测试→选择"""
# 步骤1:特征分析+可视化
print("===== 步骤1:数据特征分析 =====")
features = self.analyzer.analyze(vectors)
self.analyzer.visualize("data_features.png")
# 步骤2:算法匹配
print("\n===== 步骤2:算法规则匹配 =====")
candidates = self.rule_engine.match(features)
print(f"匹配到 {len(candidates)} 个候选算法:")
for name, params in candidates:
print(f"- {name}: {params}")
# 步骤3:基准测试+可视化
print("\n===== 步骤3:性能基准测试 =====")
self.benchmark = IndexBenchmark(vectors, query_vectors, k, self.recall_threshold)
self.benchmark.run(candidates)
self.benchmark.visualize("benchmark_result.png")
# 步骤4:选择最优索引
print("\n===== 步骤4:最优索引选择 =====")
self.best_index = self.benchmark.select_best()
return self.best_index
# 生产级测试
if __name__ == "__main__":
# 1. 加载/生成向量数据(生产级可替换为真实Embedding)
np.random.seed(42)
vectors = np.random.rand(100000, 256).astype(np.float32) # 10万条向量
query_vectors = np.random.rand(1000, 256).astype(np.float32) # 1000条查询
# 2. 初始化智能选择器
selector = IntelligentIndexSelector(recall_threshold=0.95)
# 3. 全流程运行
best_index = selector.run(vectors, query_vectors, k=10)
# 4. 输出最终结果
if best_index:
print(f"\n===== 生产级部署建议 =====")
print(f"推荐索引:{best_index['name']}")
print(f"部署参数:{selector.rule_engine.rules[best_index['name']]['params']}")
print(f"性能承诺:召回率≥{selector.recall_threshold}, QPS≥{best_index['qps']:.0f}")