最基础的神经网络可视化 包括源码
flyfish
多层感知机(Multilayer Perceptron, MLP)是最经典、最基础的神经网络模型之一,属于前馈神经网络(Feedforward Neural Network)的范畴。理解 MLP 的原理是掌握更复杂神经网络(如 CNN、RNN、Transformer)的基础。
输入层 (Input Layer) → 隐藏层 (Hidden Layer) → 输出层 (Output Layer)
多层感知机(MLP)由输入层、一个或多个隐藏层以及输出层组成。每一层都包含若干节点(神经元),这些节点通过加权连接与相邻层的节点相连。
例如,一个3层MLP是一个带两个隐藏层的全连接多层感知机(Fully Connected MLP),属于前馈神经网络(Feedforward Neural Network)的一种。
MLP的层数计数通常不算输入层(因为输入层只是接收数据,没有权重、偏置或激活计算),而是按隐藏层+输出层的数量来算。
所以"3层MLP"对应的就是:2个隐藏层 + 1个输出层
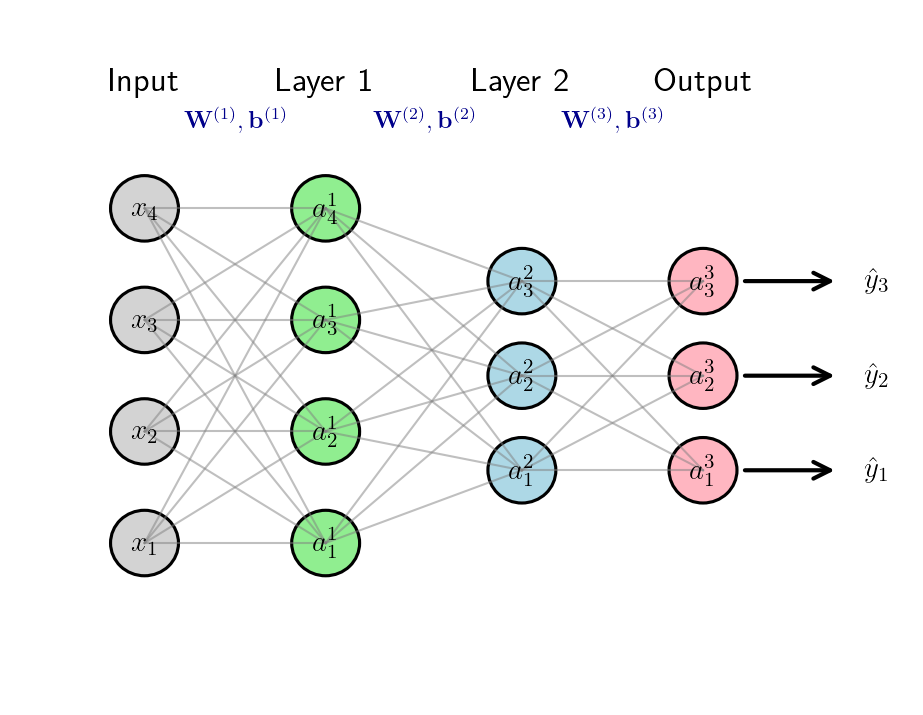
此图源码在文末
输入层 :维度为4(输入特征是x1∼x4x_1 \sim x_4x1∼x4);
隐藏层1 :包含4个神经元(a1(1)∼a4(1)a_1^{(1)} \sim a_4^{(1)}a1(1)∼a4(1)),激活函数为ReLU;
隐藏层2 :包含3个神经元(a1(2)∼a3(2)a_1^{(2)} \sim a_3^{(2)}a1(2)∼a3(2)),激活函数也为ReLU;
输出层 :包含3个神经元(a1(3)∼a3(3)a_1^{(3)} \sim a_3^{(3)}a1(3)∼a3(3)),激活函数为Softmax(对应多分类任务)。
。
输入向量
x=[x1x2x3x4] \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} x= x1x2x3x4
第一层激活(a(1)\mathbf{a}^{(1)}a(1))
a(1)=ReLU(W(1)x+b(1)) \mathbf{a}^{(1)} = \text{ReLU}\left( \mathbf{W}^{(1)}\mathbf{x} + \mathbf{b}^{(1)} \right) a(1)=ReLU(W(1)x+b(1))
第二层激活(a(2)\mathbf{a}^{(2)}a(2))
a(2)=ReLU(W(2)a(1)+b(2)) \mathbf{a}^{(2)} = \text{ReLU}\left( \mathbf{W}^{(2)}\mathbf{a}^{(1)} + \mathbf{b}^{(2)} \right) a(2)=ReLU(W(2)a(1)+b(2))
输出
y^=[y^1y^2y^3]=a(3)=[a1(3)a2(3)a3(3)]=Softmax(W(3)a(2)+b(3)) \hat{\mathbf{y}} = \begin{bmatrix} \hat{y}_1 \\ \hat{y}_2 \\ \hat{y}_3 \end{bmatrix} = \mathbf{a}^{(3)} = \begin{bmatrix} a_1^{(3)} \\ a_2^{(3)} \\ a_3^{(3)} \end{bmatrix} = \text{Softmax}\left( \mathbf{W}^{(3)}\mathbf{a}^{(2)} + \mathbf{b}^{(3)} \right) y^= y^1y^2y^3 =a(3)= a1(3)a2(3)a3(3) =Softmax(W(3)a(2)+b(3))
一个3层MLP可以用数学方式表示为一个复合函数:
a(l)=g(l)(W(l)a(l−1)+b(l)) \boldsymbol{a}^{(l)} = g^{(l)}\left( \boldsymbol{W}^{(l)}\boldsymbol{a}^{(l-1)} + \boldsymbol{b}^{(l)} \right) a(l)=g(l)(W(l)a(l−1)+b(l))
a(l)=[a1(l)a2(l)⋮anl(l)]=g(l)([w1,1(l)w1,2(l)...w1,nl−1(l)w2,1(l)w2,2(l)...w2,nl−1(l)⋮⋮⋱⋮wnl,1(l)wnl,2(l)...wnl,nl−1(l)][a1(l−1)a2(l−1)⋮anl−1(l−1)]+[b1(l)b2(l)⋮bnl(l)]) \boldsymbol{a}^{(l)} = \begin{bmatrix} a_1^{(l)} \\ a_2^{(l)} \\ \vdots \\ a_{n_l}^{(l)} \end{bmatrix} = g^{(l)}\left( \begin{bmatrix} w_{1,1}^{(l)} & w_{1,2}^{(l)} & \dots & w_{1,n_{l-1}}^{(l)} \\ w_{2,1}^{(l)} & w_{2,2}^{(l)} & \dots & w_{2,n_{l-1}}^{(l)} \\ \vdots & \vdots & \ddots & \vdots \\ w_{n_l,1}^{(l)} & w_{n_l,2}^{(l)} & \dots & w_{n_l,n_{l-1}}^{(l)} \end{bmatrix} \begin{bmatrix} a_1^{(l-1)} \\ a_2^{(l-1)} \\ \vdots \\ a_{n_{l-1}}^{(l-1)} \end{bmatrix} + \begin{bmatrix} b_1^{(l)} \\ b_2^{(l)} \\ \vdots \\ b_{n_l}^{(l)} \end{bmatrix} \right) a(l)= a1(l)a2(l)⋮anl(l) =g(l) w1,1(l)w2,1(l)⋮wnl,1(l)w1,2(l)w2,2(l)⋮wnl,2(l)......⋱...w1,nl−1(l)w2,nl−1(l)⋮wnl,nl−1(l) a1(l−1)a2(l−1)⋮anl−1(l−1) + b1(l)b2(l)⋮bnl(l)
符号说明
W(l)\boldsymbol{W}^{(l)}W(l)和b(l)\boldsymbol{b}^{(l)}b(l)分别是第lll层的权重矩阵和偏置向量。
a(l)\boldsymbol{a}^{(l)}a(l)是第lll层所有神经元的激活输出。
g(l)g^{(l)}g(l)是第lll层的激活函数(例如sigmoid、tanh、ReLU、Softmax)。
2. 梯度下降
训练神经网络的目标是找到一组最优参数θ∗\theta^*θ∗,使得训练数据集上的损失函数L(θ)\mathcal{L}(\theta)L(θ)(符号L)最小化。损失函数(也称为代价函数)用于衡量网络预测结果与实际目标值之间的差异。这个优化问题可以形式化表示为:
θ∗=argminθL(θ) \theta^* = \arg \min_{\theta} \mathcal{L}(\theta) θ∗=argθminL(θ)
其中θ={W(1),b(1),W(2),b(2),...,W(L),b(L)}\theta = \{ \mathbf{W}^{(1)}, \mathbf{b}^{(1)}, \mathbf{W}^{(2)}, \mathbf{b}^{(2)}, ..., \mathbf{W}^{(L)}, \mathbf{b}^{(L)} \}θ={W(1),b(1),W(2),b(2),...,W(L),b(L)}代表神经网络的所有模型参数(权重和偏置)。
使用梯度下降来训练多层感知机(MLP)。梯度下降是一种优化算法,通过调整网络的模型参数,最小化预测输出与实际输出之间的误差。
梯度下降算法
步骤0 :随机初始化权重和偏置参数:θ={W(1),b(1),W(2),b(2),...,W(L),b(L)}\theta = \{ \mathbf{W}^{(1)}, \mathbf{b}^{(1)}, \mathbf{W}^{(2)}, \mathbf{b}^{(2)}, ..., \mathbf{W}^{(L)}, \mathbf{b}^{(L)} \}θ={W(1),b(1),W(2),b(2),...,W(L),b(L)}
步骤1 :计算代价函数L(θ)\mathcal{L}(\theta)L(θ),它用于衡量模型在数据集上的表现优劣。
(对应公式:θ∗=minθL(θ)=minθ1N∑i=1Nℓ(y(i),fθ(x(i)))\theta^* = \min_{\theta} \mathcal{L}(\theta) = \min_{\theta} \frac{1}{N} \sum_{i=1}^{N} \ell\left(y^{(i)}, f_{\theta}\left(x^{(i)}\right)\right)θ∗=minθL(θ)=minθN1∑i=1Nℓ(y(i),fθ(x(i))))
这个公式是训练集平均损失的最小化目标
θ∗\theta^*θ∗:表示模型的"最优参数集合" (比如MLP里所有的权重W(1),W(2)...\mathbf{W}^{(1)}, \mathbf{W}^{(2)}...W(1),W(2)...和偏置b(1),b(2)...\mathbf{b}^{(1)}, \mathbf{b}^{(2)}...b(1),b(2)...)。
minθ\min_{\theta}minθ:表示**"对参数θ\thetaθ求最小值"------我们要找的是能让后面的损失函数最小的那组θ\thetaθ。
L(θ)\mathcal{L}(\theta)L(θ):表示 整个训练集的"代价函数"(也叫"全局损失"),衡量模型在所有训练样本上的整体误差。
NNN:表示 训练集的样本数量**(比如有100个训练样本,N=100N=100N=100)。
ℓ(y(i),y^(i))\ell(y^{(i)}, \hat{y}^{(i)})ℓ(y(i),y^(i)):表示第iii个样本的"单个样本损失" :
y(i)y^{(i)}y(i)是第iii个样本的真实标签 (比如分类任务中是"猫/狗"对应的0/1,回归任务中是真实房价);
y^(i)\hat{y}^{(i)}y^(i)是模型对第iii个样本的预测值 (比如分类任务中是"猫"的概率,回归任务中是预测房价);
ℓ(⋅)\ell(\cdot)ℓ(⋅)是"损失函数"(比如分类用交叉熵 ,回归用均方误差 ),专门衡量"预测值和真实值的差异有多大"。
步骤2 :计算代价函数关于每个参数的梯度∇θL(θt)\nabla_{\theta} \mathcal{L}(\theta_t)∇θL(θt)
步骤3 :通过如下公式更新参数:
θt+1=θt−η⋅∇θL(θt) \theta_{t+1} = \theta_t - \eta \cdot \nabla_{\theta} \mathcal{L}(\theta_t) θt+1=θt−η⋅∇θL(θt)
其中η\etaη(eta)是学习率,它决定了每次迭代ttt中参数更新的幅度。
这个公式描述的是"从当前迭代的参数 ,更新到下一次迭代的参数 "的规则:
θt\theta_tθt:表示第ttt次迭代时的模型参数 (比如MLP里的权重/偏置);
θt+1\theta_{t+1}θt+1:表示第t+1t+1t+1次迭代后的新参数 (我们要得到的更新后结果);
η\etaη:学习率 (一个正数,比如0.01),控制参数每次更新的"步长"(走多远);
∇θL(θt)\nabla_{\theta} \mathcal{L}(\theta_t)∇θL(θt):代价函数在当前参数θt\theta_tθt处的梯度 ------它是"代价函数在当前参数点,上升速度最快的方向"(可以理解为"代价变大的方向")。
梯度∇θL(θt)\nabla_{\theta} \mathcal{L}(\theta_t)∇θL(θt)是"代价函数上升的方向",所以减去梯度 ,就相当于让参数朝着"代价函数减小的方向"移动------这正是"梯度下降"的重点:每次迭代都把参数往"让代价函数变小"的方向调一点,逐步靠近代价最小的最优参数θ∗\theta^*θ∗。
cpp
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Circle, FancyArrowPatch
from matplotlib.lines import Line2D
plt.rcParams['text.usetex'] = True
fig, ax = plt.subplots(figsize=(16, 9))
ax.set_xlim(0, 12)
ax.set_ylim(0, 9.5)
ax.axis('off')
layer_x = [1.8, 4.2, 6.8, 9.2, 11.5]
# 输入层:4 个节点
input_y = np.linspace(2.2, 6.8, 4)
for i, y in enumerate(input_y):
circle = Circle((layer_x[0], y), 0.45, fill=True, color='lightgray', ec='black', lw=1.5)
ax.add_patch(circle)
ax.text(layer_x[0], y, rf'$x_{{{i+1}}}$', ha='center', va='center', fontsize=14)
# Layer 1:4 个节点(ReLU)
layer1_y = np.linspace(2.2, 6.8, 4)
for i, y in enumerate(layer1_y):
circle = Circle((layer_x[1], y), 0.45, fill=True, color='lightgreen', ec='black', lw=1.5)
ax.add_patch(circle)
ax.text(layer_x[1], y, rf'$a_{{{i+1}}}^{(1)}$', ha='center', va='center', fontsize=14)
# Layer 2:3 个节点(ReLU)
layer2_y = np.linspace(3.2, 5.8, 3)
for i, y in enumerate(layer2_y):
circle = Circle((layer_x[2], y), 0.45, fill=True, color='lightblue', ec='black', lw=1.5)
ax.add_patch(circle)
ax.text(layer_x[2], y, rf'$a_{{{i+1}}}^{(2)}$', ha='center', va='center', fontsize=14)
# 输出层:3 个节点(Softmax)
output_y = np.linspace(3.2, 5.8, 3)
for i, y in enumerate(output_y):
circle = Circle((layer_x[3], y), 0.45, fill=True, color='lightpink', ec='black', lw=1.5)
ax.add_patch(circle)
ax.text(layer_x[3], y, rf'$a_{{{i+1}}}^{(3)}$', ha='center', va='center', fontsize=14)
# 输出箭头
arrow = FancyArrowPatch((layer_x[3] + 0.5, y), (layer_x[4] - 0.5, y),
arrowstyle='->', mutation_scale=20, lw=2, color='black')
ax.add_patch(arrow)
ax.text(layer_x[4], y, rf'$\hat{{y}}_{{{i+1}}}$', ha='center', va='center', fontsize=14)
# 全连接线
def draw_connections(x1, y1s, x2, y2s, color='gray', alpha=0.5):
for y1 in y1s:
for y2 in y2s:
ax.plot([x1, x2], [y1, y2], color=color, alpha=alpha, lw=1, zorder=1)
draw_connections(layer_x[0], input_y, layer_x[1], layer1_y)
draw_connections(layer_x[1], layer1_y, layer_x[2], layer2_y)
draw_connections(layer_x[2], layer2_y, layer_x[3], output_y)
# 层标题
ax.text(layer_x[0], 8.4, 'Input', ha='center', fontsize=16, fontweight='bold')
ax.text(layer_x[1], 8.4, 'Layer 1', ha='center', fontsize=16, fontweight='bold')
ax.text(layer_x[2], 8.4, 'Layer 2', ha='center', fontsize=16, fontweight='bold')
ax.text(layer_x[3], 8.4, 'Output', ha='center', fontsize=16, fontweight='bold')
# 权重与偏置标注
ax.text((layer_x[0] + layer_x[1]) / 2, 7.9,
r'$\mathbf{W}^{(1)}, \mathbf{b}^{(1)}$', ha='center', fontsize=12, color='darkblue')
ax.text((layer_x[1] + layer_x[2]) / 2, 7.9,
r'$\mathbf{W}^{(2)}, \mathbf{b}^{(2)}$', ha='center', fontsize=12, color='darkblue')
ax.text((layer_x[2] + layer_x[3]) / 2, 7.9,
r'$\mathbf{W}^{(3)}, \mathbf{b}^{(3)}$', ha='center', fontsize=12, color='darkblue')
plt.tight_layout()
plt.show()
# 保存
# plt.savefig('neural_network_usetex.pdf', bbox_inches='tight', dpi=300)
# plt.savefig('neural_network_usetex.png', bbox_inches='tight', dpi=300)