向量组的秩
向量组的秩是线性代数的核心概念 ,它描述了向量组中线性无关向量的最大个数,反映了向量组的 "本质维度",是判断向量组线性相关性、求解线性方程组、分析矩阵结构的关键工具。
一、核心定义
1. 极大线性无关组
给定一个向量组 α1,α2,...,αs(向量可以是 n 维列向量或行向量),如果它的一个部分组 αi1,αi2,...,αir 满足两个条件:
- 线性无关:该部分组中没有任何一个向量可以由其余向量线性表示。
- 极大性:从原向量组中任意添加一个剩余向量到该部分组,新的向量组都会变成线性相关。
则称这个部分组为原向量组的 极大线性无关组。
注意:
- 一个向量组的极大线性无关组不唯一。例如向量组 α1=(1,0),α2=(0,1),α3=(1,1),{α1,α2} 和 {α1,α3} 都是它的极大线性无关组。
- 仅含零向量的向量组没有极大线性无关组。
2. 向量组的秩
向量组的所有极大线性无关组所含向量的个数是相同的 ,这个公共的个数称为该向量组的秩,记作 r(α1,α2,...,αs) 或 rank(α1,α2,...,αs)。
关键结论:
- 若向量组仅含零向量,秩为 0。
- 若向量组线性无关,则它的极大线性无关组就是自身,秩等于向量组的向量个数 s,即 r=s。
- 若向量组线性相关,则 r<s。
二、向量组的秩与矩阵的秩的关系
在 AI 领域,我们通常将向量组按列或按行排列成矩阵,利用矩阵的秩来求向量组的秩,这是最常用的计算方法。
1. 基本定理
设 A 是一个 m×n 矩阵:
- 矩阵 A 的列秩:矩阵的 n 个列向量构成的向量组的秩。
- 矩阵 A 的行秩:矩阵的 m 个行向量构成的向量组的秩。
- 核心定理 :矩阵的列秩 = 行秩 = 矩阵的秩(矩阵的秩定义为最高阶非零子式的阶数)。
这个定理建立了向量组的秩与矩阵的秩的桥梁,也是 AI 中矩阵运算的理论基础(比如神经网络中的特征降维)。
2. 计算向量组的秩的方法(核心步骤)
对于 n 维列向量组 α1,α2,...,αs,计算秩的步骤:
- 构造矩阵:将向量组按列排列成矩阵 A=(α1,α2,...,αs)(n×s 矩阵)。
- 初等行变换 :对矩阵 A 做初等行变换,将其化为 行阶梯形矩阵。
- 数非零行的行数 :行阶梯形矩阵中非零行的行数就是矩阵的秩,也就是原向量组的秩。
3. 初等行变换不改变矩阵列向量组的线性关系
将α1,α2,α3,α4按列构成矩阵,对其做初等行(只做行变换)变换化为行最简形:
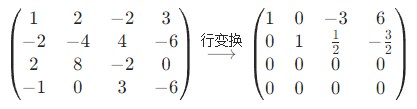
行最简形有 2 个非零行,故向量组的秩为 2,极大线性无关组含 2 个向量(不唯一),常见的有:
- {α1,α2}(行最简形 "首非零元" 对应的列);
- {α1,α3}(α3不能由α1线性表示);
- {α1,α4}(α4不能由α1线性表示)。
以 **极大线性无关组{α1,α2}**为例,根据行最简形的列向量关系,原向量满足:
