当工具变量遇上深度学习：DeepIV如何看透因果？

引子：从"涨价"不一定"减量"说起

生活中有许多看似反常的经济现象。比如，每逢节假日，机票价格飙升，但出游的人数却不减反增，各大航司的机票销售依旧火爆。如果我们天真地把"价格"和"销量"这两个数据点直接拿给一个机器学习模型，它很可能会得出一个令人啼笑皆非的结论："涨价能提升销量！"

这显然违背了基本的经济学常识。我们都知道，这个现象的背后其实隐藏着一个关键的"混杂变量 "（Confounding Variable）------节假日。是节假日这个因素，同时推高了人们的出游需求（导致销量增加）和航空公司的定价（导致价格上涨）。我们观测到的，只是价格与销量在节假日影响下的"伪相关"，而非两者之间真实的因果关系。

相关不等于因果 ，这句统计学领域的古老格言，在数据科学时代显得愈发重要。如果我们无法剥离"节假日"这类混杂因素的干扰，就无法回答那个对航空公司至关重要的反事实问题 （Counterfactual Question）：如果在同一个节假日，我们不涨价，甚至降价，机票的销量到底会变成多少？

回答这类"如果......会怎样？"的问题，就是因果推断（Causal Inference）的核心使命。它试图超越简单的预测，去理解一个变量对另一个变量的真实影响。在现实世界中，混杂因素往往是复杂、多维，甚至是无法被直接观测的（比如前文论文提到的、无法直接观测的"行业会议"需求），这让因果推断变得极具挑战性。

幸运的是，经济学家们在近百年的探索中，磨砺出了一件强大的武器------工具变量法 （Instrumental Variable, IV）。而今天，当这件经典武器与现代深度学习的强大力量相结合时，一个名为 DeepIV 的全新框架应运而生。它由微软研究院与高校学者共同提出，旨在利用神经网络的威力，更精准、更灵活地回答复杂场景下的反事实问题。

这篇文章，就让我们以公众号《阿水实证通》的风格，用直觉和案例，带你一起读懂 DeepIV 的精髓，看看它是如何从机票定价和广告位排序这些真实场景中，看透数据表象，洞察因果本质的。

核心直觉：DeepIV 如何"骗过"模型，找到真相？

要理解 DeepIV，我们得先从它的两个"积木"------工具变量（IV）和两阶段最小二乘法（2SLS）------的直觉开始。

什么是工具变量？一个绝佳的"自然实验"

想象一下，我们要研究机票价格（处理变量 P）对销量（结果变量 Y）的真实影响，但又受到了无法观测的"会议需求"（混杂因素 E）的干扰。这时，我们需要找到一个"局外人"，它就是工具变量（Z）。这个"局外人"必须满足三个苛刻的条件：

1. 相关性 (Relevance)：它必须能影响机票价格 P。例如，燃油成本的波动。航空公司会根据燃油成本调整票价，所以燃油成本与票价是相关的。

2. 排他性 (Exclusion)：它只能通过影响票价来影响销量 Y，而不能有任何"秘密通道"直接影响销量。燃油成本的变动，对于乘客来说是无感的，它不会直接决定乘客是否要出行，只会通过改变机票价格来间接影响他们的决策。

3. 外生性 (Exogeneity / Unconfoundedness)：它必须独立于那个未被观测的混杂因素 E。燃油成本是全球性的市场因素，它与某地是否要开一场特定的行业会议，基本上是毫无关系的。

图1：这张图展示了航空票价与需求的因果结构示意，突出价格、销量、节假日、会议需求和燃油成本等变量之间的关系。

有了同时满足这三个条件的工具变量，我们就相当于拥有了一个**"准自然实验"**。燃油成本的每一次随机波动，都像是上帝在帮我们做实验，它为机票价格带来了一部分独立于"会议需求"的、干净的、外生的变动。正是利用这部分"干净"的变动，我们才有可能窥见价格对销量的真实因果效应。

经典IV的"两步走"战略 (2SLS)

传统的工具变量法，最经典的就是两阶段最小二乘法（2SLS），它的思路非常直观：

• 第一阶段：净化处理变量我们不用那个被"会议需求 E"污染过的真实价格 P，而是建立一个模型，用工具变量 Z（燃油成本）和其他可观测的协变量 X（如节假日、星期几）来预测价格。

  P_predicted = f(Z, X) 这个预测出来的价格 P_predicted，因为它的信息来源是"干净"的 Z 和 X，所以它在很大程度上过滤掉了来自 E 的污染。

• 第二阶段：估计因果效应 我们再用这个"净化"过的价格 P_predicted 去和结果 Y（销量）做回归分析，从而得到价格对销量的"纯净"的因果效应。

  Y = g(P_predicted, X)

DeepIV的升级玩法：用神经网络"两步走"

DeepIV 继承了 2SLS 的"两步走"思想，但用更强大、更灵活的深度神经网络替换了其中的线性模型，从而能捕捉复杂的非线性关系和异质性效应。

第一阶段：更强大的"天气预报员"

DeepIV 的第一阶段不再是仅仅预测一个单一的价格值，而是用一个深度神经网络（论文中称为 Treatment Network ）去学习一个完整的条件概率分布 F(p|x,z)。

2SLS 的思想很巧妙，但它通常依赖一个很强的假设：线性和同质性。也就是说，它假设价格每变动一元，对所有类型乘客、在所有时间点，销量的影响都是相同的。这在复杂的现实世界中，显然过于简化了。

这意味着，给定当前的协变量 X（如节假日）和工具变量 Z（如燃油成本），模型会告诉你价格 P 可能的取值范围及其对应的概率。比如，模型会预测："在这种情况下，机票价格有 50% 的可能性是 1000 元，30% 的可能性是 1200 元，20% 的可能性是 800 元。"

这个升级非常关键，因为它保留了处理变量 P 的所有不确定性信息，为第二阶段的精确求解铺平了道路。这就像一个更高级的天气预报，它不仅告诉你"明天可能下雨"，还告诉你"明天降雨概率为 80%，雨量大约在 10-20 毫米之间"。

第二阶段：在"反事实"的积分迷宫中寻找最优解

这是 DeepIV 最为精妙的部分。我们先思考一下，标准监督学习的目标是什么？是让模型的预测值 E[y|p,x] 尽可能地接近观测到的真实值 y。但我们在一开始就点明了，这个 E[y|p,x] 是被混杂因素 E 污染过的，它不等于我们真正想要的那个反事实函数 h(p,x)。

DeepIV 的做法则完全不同。它的优化目标，是让我们正在寻找的那个反事实函数 h(p,x)，在经过第一阶段预测出的价格分布 F(p|x,z) 的"洗礼"后，其期望结果能与真实的观测结果 y 对齐。

用数学语言来说，DeepIV 的损失函数是：

Loss = ( y_observed - ∫ h(p,x) dF(p|x,z) )²

这个公式可能看起来有点吓人，我们把它翻译成大白话：

1. h(p,x)：这是我们想要求的"天机"，即在给定协变量 x 的情况下，如果价格是 p，那么销量应该是多少。这个函数由一个神经网络（Outcome Network）来近似。

2. dF(p|x,z)：这是第一阶段神经网络给出的"价格可能性报告"。

3. ∫ h(p,x) dF(p|x,z)：这个积分的直观意义是，根据"价格可能性报告"，把所有可能的价格代入"天机函数"h(p,x) 中算一遍，然后根据各自的可能性大小做一个加权平均。它代表了**"在工具变量 Z 看来，销量 Y 的期望值应该是多少"**。

4. y_observed：这是我们实际观测到的真实销量。

因此，整个损失函数要做的，就是调整"天机函数"h(p,x)（也就是训练 Outcome Network），使得它推算出的期望销量，与我们在现实中观测到的真实销量，尽可能地接近。

实践检验：DeepIV 在真实与模拟世界中的表现

理论讲得再好，终究要看疗效。DeepIV 的论文通过一系列精心设计的实验，展示了它在不同场景下的强大能力。

案例一：模拟的航空票价，洞察非线性效应

研究者首先构建了一个更复杂的模拟航空票价环境。在这个环境中，不仅有季节性因素（协变量 X）和燃油价格（工具变量 Z），还引入了 7 种不同价格敏感度的"乘客类型"（异质性），以及一个可调节的、代表"未观测会议需求"强度的参数 ρ。ρ 越大，意味着普通机器学习模型面临的挑战越大。

通过这种方式，DeepIV 的第二阶段网络 h(p,x) 被"逼"着去学习那个不受混杂因素 E 干扰的、真正的结构性关系 。因为它优化的目标不是去拟合那个被污染的 y，而是去满足由"干净"的工具变量 Z 所定义的那个积分方程。这就好比，我们不再直接临摹一幅被弄脏的画，而是根据一位可靠的修复师（工具变量）提供的修复指南（积分方程），来还原这幅画本来的面目。

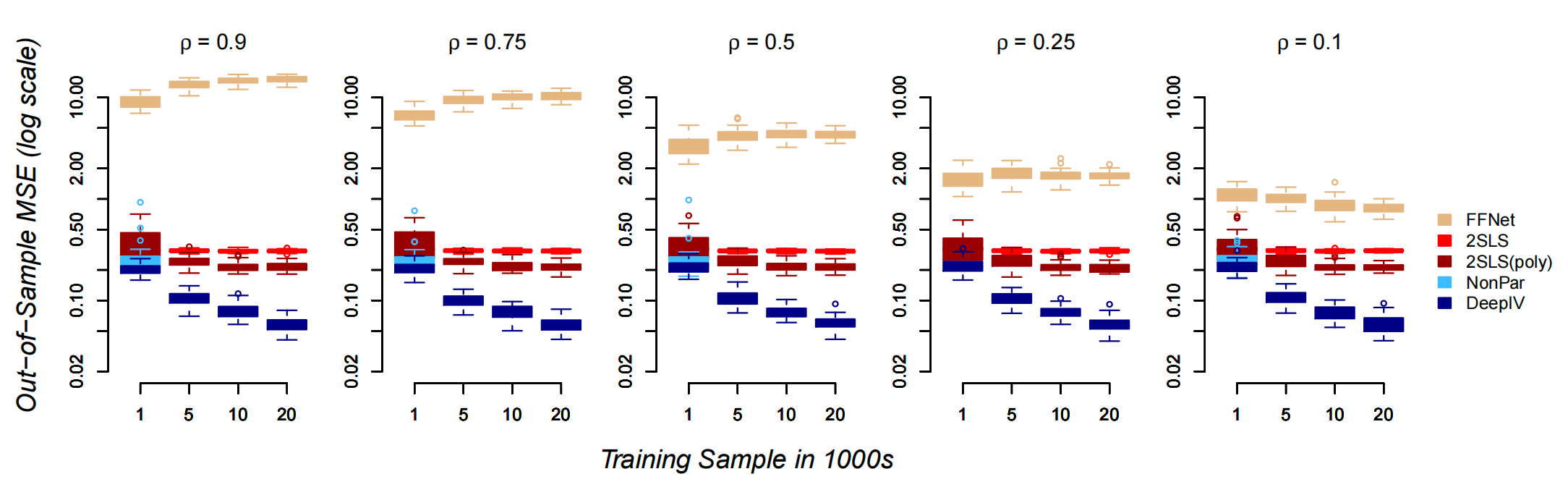
实验对比了 DeepIV、传统的 2SLS、更复杂的非参数 IV 方法（NonPar），以及一个直接用深度学习做预测的朴素模型（FFNet）。

图2：这张图展示了在不同内生性水平（ρ）和样本量下，各种方法在结构性反事实预测上的误差表现，对比了 DeepIV、2SLS、非参数 IV 和朴素深度网络的差异。

核心发现：

现在，模型不再能直接看到"乘客类型=1"这样的标签，而是必须自己从一张 28x28 像素的图片中，学习到这个乘客属于哪一类，以及这类乘客的价格敏感度是怎样的。

这个实验的意义在于，它检验了 DeepIV 端到端学习的能力------即从原始的高维特征（图片）中，自动提取出对因果效应分析有用的信息。

• DeepIV 表现最佳：在所有实验设置下，DeepIV 的反事实预测误差都是最低的，并且随着训练样本量的增加，其优势愈发明显。这证明了它捕捉复杂非线性关系和异质性效应的能力。

• 传统 IV 方法的局限：2SLS 因为其线性和同质性假设，性能很快达到瓶颈，即使给再多数据也无法提升。非参数 IV 方法虽然比 2SLS 好，但计算成本极高，在大样本量下难以应用。

• 朴素深度学习的"惨败"：直接做预测的 FFNet 表现最差。因为它错误地学习了"高价高销量"的伪相关，当测试时需要预测一个固定价格下的销量时，它便完全失准。这恰恰凸显了因果推断的必要性。

案例二：从手写数字识别，看懂高维特征

现实世界的数据特征往往不是简单的数字，而可能是图片、文本等高维信息。为了模拟这种情况，研究者做了一个巧妙的实验：他们将模拟中的 7 种"乘客类型"，替换成了 MNIST 数据集里代表数字 0-7 的手写图片。

核心发现：

• DeepIV 依旧能打：即使面对高维的图片特征，DeepIV 的表现依然远超其他方法，成功地从像素中恢复了反事实关系。

• 超参数与验证的重要性 ：在高维场景下，模型的结构、正则化等超参数的选择变得至关重要。论文展示了他们设计的**"因果验证"**（Causal Validation）方法是有效的------在验证集上损失更小的模型，在最终的真实反事实预测任务中也表现更好。这为在实践中应用 DeepIV 提供了可行的调优路径。

案例三：微软 Bing 广告位的真实世界应用

最激动人心的，莫过于将 DeepIV 应用于真实的商业场景。研究团队利用了微软 Bing 搜索引擎的广告数据，来分析广告位 （Position，即排在第几位）对点击率（Click-Through Rate, CTR）的真实因果效应。

这个问题同样充满了挑战。通常，最吸引人的广告（比如用户正在搜索的品牌官网）也最有可能排在第一位。因此，我们观测到的"高排位、高点击"现象，同样可能是一个伪相关。

这里的工具变量是什么呢？是 Bing 内部进行的 A/B 实验。搜索引擎会经常进行各种算法的小范围测试，这些测试会随机地改变某些广告的排序算法，从而导致广告位的随机变化。这个"实验 ID"就成了一个完美的工具变量！

研究团队特别关注了四种不同类型的查询，以验证 DeepIV 是否能捕捉到异质性的广告位效应：

1. On-Brand: 品牌方为自己的品牌关键词出价 (如：可口可乐竞价"可口可乐")

2. Off-Brand: 竞争对手为品牌关键词出价 (如：百事可乐竞价"可口可乐")

3. On-Nav: 用户在搜索框里输入了网址 (如：搜索"www.coke.com")

4. Off-Nav: 竞争对手为网址出价

DeepIV的优势边界与中国场景下的思考

通过上述解读，我们可以总结出 DeepIV 的核心优势与适用边界：

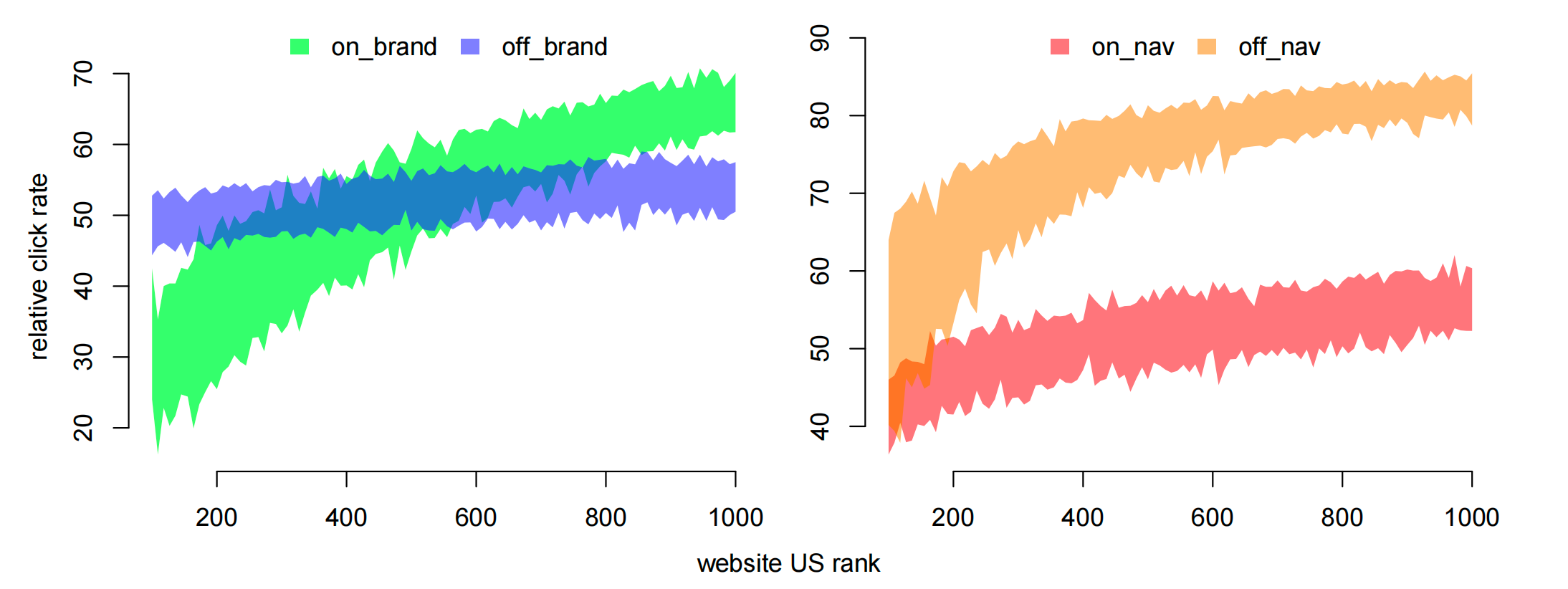
图4：这张图展示了从广告位第1名掉到第2名时点击率下降的幅度在不同广告主和查询类型中的差异，用于刻画 on-brand/off-brand 以及 on-nav/off-nav 的异质性位置效应。

核心发现：

• 自动化复现经典研究：DeepIV 仅需输入原始的文本数据（查询词、广告主网址）和实验 ID，就成功复现了一项早前研究（Goldman & Rao, 2014）需要大量人工特征工程和分类才能得出的结论。

• 发现有趣的异质性效应：如图4所示，DeepIV 发现了：

  • 对于 On-Brand 查询，广告排位对小品牌比对大品牌更重要。因为大品牌本身就有很强的吸引力，即使用户在第二、三位看到它，也会去点击。

  • 对于 On-Nav 查询（用户本来就想去官网），排在第一还是第二几乎没有差别。但对于 Off-Nav 查询，排位的价值就大得多。

• 量化真实效应：一个直接用数据训练的非因果模型会高估排位的价值，认为从第一位掉到第二位，点击率会暴跌 70%。而 DeepIV 给出的因果估计则更为合理，认为平均只会下降12%。

优势：

• 灵活性与非线性：能够捕捉传统线性模型无法刻画的复杂关系。

图4解读：这张图展示了从广告位第1名掉到第2名，点击率下降的百分比（纵轴）。左图对比了品牌自身（on-brand）和竞品（off-brand）的情况，可以看到对于越受欢迎的广告主（横轴靠右），on-brand的排位价值越小。右图对比了导航查询（on-nav）和非导航查询（on-nav），清晰地显示了导航查询的排位价值（蓝线）远低于非导航查询（绿线）。

• 异质性效应：能够从数据中学习不同个体、不同情境下，处理效应的差异。

• 端到端学习：可以直接处理高维原始特征（如文本、图像），减少了人工特征工程的负担。

• 可扩展性：基于随机梯度下降的优化方法，使其可以处理海量数据。

边界与挑战：

• 工具变量的质量 ：DeepIV 的所有魔力都建立在拥有一个"好"的工具变量之上。如果工具变量与处理变量的相关性很弱（弱工具变量问题），或者不满足排他性/外生性假设，那么结果同样会产生偏差。

• 计算成本：虽然比一些非参数方法高效，但两阶段的训练和积分的近似计算，仍然比简单的监督学习要昂贵。

• 可解释性：深度学习模型本身的"黑箱"特性，使得我们很难直观地理解模型到底学到了什么样的具体函数形式。

文献拓展：数字基础设施与粮食生产中的DeepIV应用

在精读完DeepIV的开创性论文后，我们再来看一个它在具体经济学研究中的应用实例：由清华大学的刘生龙、张晓明发表在《数量经济技术经济研究》上的论文**《数字基础设施与粮食生产：基于深度学习的实证证据》**。这项研究利用DeepIV，探讨了中国农村数字基础设施（如互联网接入）对家庭粮食生产的影响，为我们理解DeepIV的实际价值提供了一个绝佳的窗口。

为何采用DeepIV？OLS与2SLS的局限

研究的核心问题是：农村家庭接入互联网后，他们的粮食产量和播种面积会发生什么变化？

• OLS的困境 ：最简单的普通最小二乘法（OLS）会面临严重的内生性问题 。一方面，互联网可能通过提供非农就业信息，引导劳动力外出务工，从而减少粮食生产；另一方面，本身农业生产规模大、对信息需求更强的家庭，也可能更倾向于接入互联网。这种"双向因果"关系，使得OLS的估计结果（显示互联网接入会轻微降低粮食产量和播种面积）并不可靠。

• 2SLS的挑战 ：传统的工具变量两阶段最小二乘法（2SLS）虽然能处理内生性，但其严格的线性假设 可能与现实不符。数字基建对不同家庭（如受教育程度不同、耕地规模不同）的影响很可能是非线性的、异质性的。该研究的2SLS结果显示，互联网接入会极大降低粮食产量，其效应值远超样本均值，这暗示模型可能存在设定偏误，高估了真实影响。

正是在这种背景下，DeepIV的优势得以凸显。它既能通过工具变量处理内生性，又能借助神经网络捕捉复杂的非线性关系和异质性处理效应 。其核心框架------第一阶段估计处理（接入互联网）的条件分布F(p|x,z)，第二阶段优化包含积分的结构性损失函数------恰好能解决传统方法的痛点。

图注：该页展示了DeepIV的两阶段框架与目标函数。 公式(1)和(2)清晰地描述了DeepIV如何通过两阶段的神经网络优化，来求解结构性反事实函数，这正是其超越传统线性IV方法的核心所在。

工具变量的选择与有效性

为了解决内生性问题，该研究构建了一个巧妙的"供给冲击型"工具变量（Supply-push Instrument）：基期农村移动电话普及率 × 全国光缆线路长度。

• 逻辑：基期的移动电话普及率反映了一个地区对信息技术的历史接纳程度，而全国光缆线路长度则代表了宏观层面的供给侧推动力。这两者的交互，为当地家庭能否以及以何种成本接入互联网带来了外生的变动，且这种变动与单个家庭当期的农业生产决策无关。

• 有效性检验：研究采用了Kédagni 和 Mourifié (2020) 提出的前沿方法对工具变量的有效性进行严格检验，结果表明该工具变量满足相关性、排他性和外生性假设，是一个"好"的工具变量。

主要结论：介于OLS与2SLS之间的稳健发现

在使用DeepIV进行估计后，研究得到了更为可信和稳健的结论：

• 显著的负向影响：DeepIV的估计结果表明，数字基础设施的使用显著降低了农村家庭的播种面积和粮食产量。具体而言，接入互联网使得家庭播种面积的自然对数下降了约0.663，粮食产量的自然对数下降了约2.143。

• 效应大小居中且精度更高 ：这个效应幅度介于OLS的低估和2SLS的高估之间，显示出更强的合理性。同时，DeepIV估计出的标准误（Standard Error）比OLS和2SLS都更小，这意味着估计结果的精度更高、预测性能更优。

• 实现方式 ：该研究明确指出，其DeepIV模型是基于Python的Keras库进行两阶段神经网络训练的，这也为其他研究者复现和应用该方法提供了清晰的路径。

图注：该页展示了基于深度IV的估计结果与表4。 表4清晰地呈现了DeepIV的估计系数、标准误，并与前文的OLS和2SLS结果形成了对比，直观地展示了DeepIV在效应幅度和估计精度上的优势。

总而言之，这篇应用文献生动地展示了DeepIV如何在真实的经济学研究中发挥作用：它不仅提供了一个处理内生性的高级工具，更重要的是，它通过灵活的非线性建模，得出了比传统方法更可靠、更精确的因果效应估计，从而为我们理解数字时代下的农业转型提供了坚实的证据。

1. 挖掘中国特色的数据场景与工具变量

   • 政策断点作为工具：中国的许多政策具有明确的执行边界和时间点，这为寻找工具变量提供了天然的"实验场"。

     • 案例 ：研究新能源汽车牌照政策（如上海的免费牌照 vs. 北京的摇号）对居民购车决策、交通拥堵、空气质量的异质性影响。牌照政策本身就是一个强大的工具变量，影响购车决策，但与居民的出行偏好本身无关。DeepIV可以帮助我们精细刻画不同收入水平、不同家庭结构的居民对政策的反应差异。

     • 案例 ：环保限产政策（如秋冬季对"2+26"城市钢厂的停产要求）是研究企业生产行为、污染治理投入和市场价格波动的绝佳工具变量。DeepIV可以用来分析不同规模、不同技术水平的企业在限产压力下的反应模式。

2. 拥抱平台经济中的算法实验

   • 算法A/B测试作为工具 ：正如 Bing 的案例所示，中国庞大的互联网平台（如电商、短视频、网约车）每天都在进行大量的算法 A/B 测试。这些为了优化用户体验或商业指标而进行的随机流量分配，正是最理想的工具变量来源。

     • 案例 ：研究电商平台的推荐算法对用户消费结构和多样性的长期影响。算法版本（A vs. B）作为工具变量，影响用户看到的商品（处理变量），进而影响其最终购买行为（结果）。DeepIV可以帮助平台理解，什么样的推荐逻辑更能提升用户的长期价值，而非仅仅是短期GMV。

     • 案例 ：研究网约车平台的派单机制对司机收入和乘客等待时间的影响。不同的派单规则（工具变量）会改变司机接到的订单类型（处理变量）。DeepIV可以帮助平台设计更公平、更高效的派单系统，平衡多方利益。

对中国经济学研究的启发

DeepIV 这类方法为中国的经济学研究者和政策制定者打开了一扇新的大门。中国拥有海量的数字化场景和独特的制度环境，这为寻找和应用工具变量提供了丰富的土壤。以下是一些可能的创新方向：

• 关注非线性与异质性效应的政策评估

  • 传统的政策评估往往只给出一个平均处理效应（ATE），但这可能会掩盖重要的个体差异。DeepIV 的长处恰恰在于揭示这种异质性。

    • 案例 ：评估教育领域的政策，如"双减"或"就近入学规则"的变化。这些政策对不同家庭背景、不同学习能力的学生影响差异巨大。利用学生原所在学区、家庭收入等作为特征，政策变化作为处理，我们可以用 DeepIV 描绘出政策影响的完整图景，识别出哪些群体受益，哪些群体可能受损，从而为政策的优化调整提供依据。

• 产业应用与政务数据合作的潜力

  • 将 DeepIV 的思想应用于金融、医疗、交通等领域，并积极推动与政府部门的数据合作，能够释放巨大的社会与商业价值。

    • 案例 ：在信贷风控中，银行的LPR（贷款市场报价利率）调整可以作为研究贷款利率对企业违约风险影响的工具变量。DeepIV可以帮助银行更精准地为不同类型的中小微企业定价，实现商业可持续与普惠金融的平衡。

    • 案例 ：在公共卫生领域，不同地区疫苗接种的推广力度、宣传策略可以作为工具变量，研究疫苗接种对个人健康状况和医疗开支的长期影响。DeepIV能够帮助政府更有效地分配公共卫生资源。

结语

从经典统计学到现代机器学习，我们对因果关系的探索从未停止。DeepIV 的出现，并非是要用深度学习取代经典的因果推断思想，恰恰相反，它展示了当我们将严谨的因果识别框架 （如工具变量法）与强大的模型表达能力（如深度网络）相结合时，能够爆发出多么巨大的潜力。

对于《阿水实证通》的读者们而言，无论是身处学术界，还是奋斗在业界一线，理解 DeepIV 这类前沿方法，都将帮助我们磨亮双眼，在纷繁复杂的数据背后，看清那个真正驱动世界运转的、坚实的因果链条。