Manacher算法解决所有回文串问题
文章目录
- Manacher算法解决所有回文串问题
- 一、Manacher算法
-
- [1.1 基本概念](#1.1 基本概念)
- [1.2 中心扩展算法](#1.2 中心扩展算法)
- [1.3 manacer算法](#1.3 manacer算法)
- 二、洛谷里面算法题
-
- [2.0 Manacher 模板](#2.0 Manacher 模板)
- [2.1 ABB](#2.1 ABB)
- [2.2 ANT-Antisymmetry](#2.2 ANT-Antisymmetry)
- [2.3 拉拉队排练](#2.3 拉拉队排练)
- [2.4 最⻓双回⽂串](#2.4 最⻓双回⽂串)
- 三、Leetcode里面算法题
- 入门
- 进阶
-
- [35. 回⽂⼦串(medium)](#35. 回⽂⼦串(medium))
- [36. 最⻓回⽂⼦串(medium)](#36. 最⻓回⽂⼦串(medium))
- [37. 回⽂串分割IV(hard)](#37. 回⽂串分割IV(hard))
- [38. 分割回⽂串II(hard)](#38. 分割回⽂串II(hard))
- [39. 最⻓回⽂⼦序列(medium)](#39. 最⻓回⽂⼦序列(medium))
- [40. 让字符串成为回⽂串的最⼩插⼊次数(hard)](#40. 让字符串成为回⽂串的最⼩插⼊次数(hard))
- 总结
一、Manacher算法

1.1 基本概念


1.2 中心扩展算法



代码如下(示例):
c
string t, s;
int m, n;
// 以求解最⻓回⽂⼦串为例
int fun()
{
// 预处理字符串
cin >> t; m = t.size();
s += ' ';
for (auto ch : t)
{
s += '#';
s += ch;
}
s += "##";
n = s.size() - 2;
int ret = 1;
// 中⼼扩展算法
for (int i = 1; i <= n; i++)
{
int d = 1; // 枚举向右向左的距离
while (s[i - d] == s[i + d]) d++;
// d
ret = max(ret, d - 1);
}
return ret;
}1.3 manacer算法
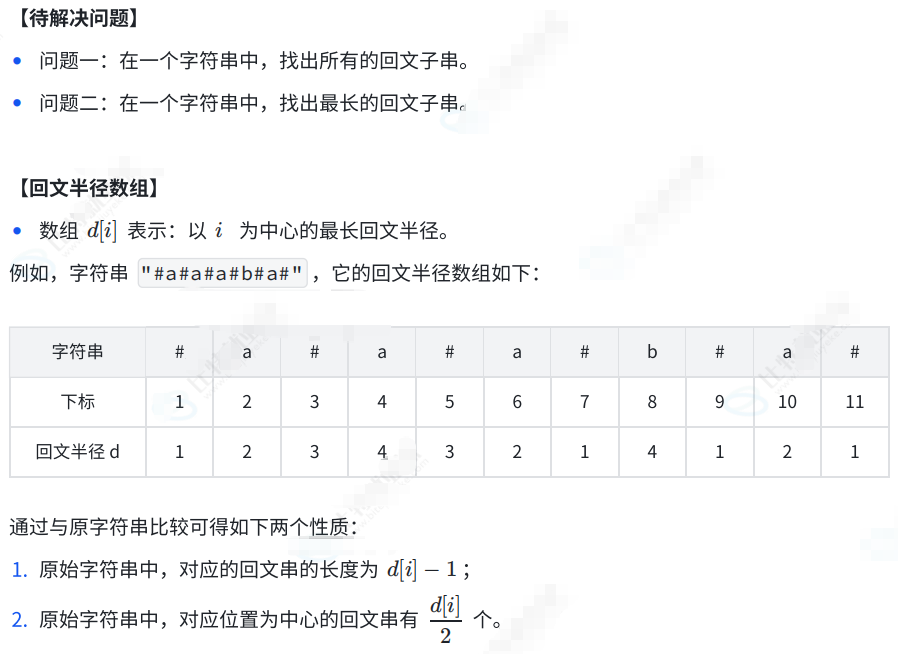



代码如下(示例):
c
string t, s;
int n, d[N];
void init()
{
cin >> t;
s = ' ';
for (auto ch : t)
{
s += '#'; s += ch;
}
s += "##";
n = s.size() - 2;
}
void get_d()
{
d[1] = 1; // 初始化
for (int i = 2, l = 1, r = 1; i <= n; i++)
{
int len = r >= i ? min(d[r - i + l], r - i + 1) : 1;
while (s[i + len] == s[i - len]) len++;
if (i + len - 1 > r) r = i + len - 1, l = i - len + 1;
d[i] = len;
}
}二、洛谷里面算法题
2.0 Manacher 模板
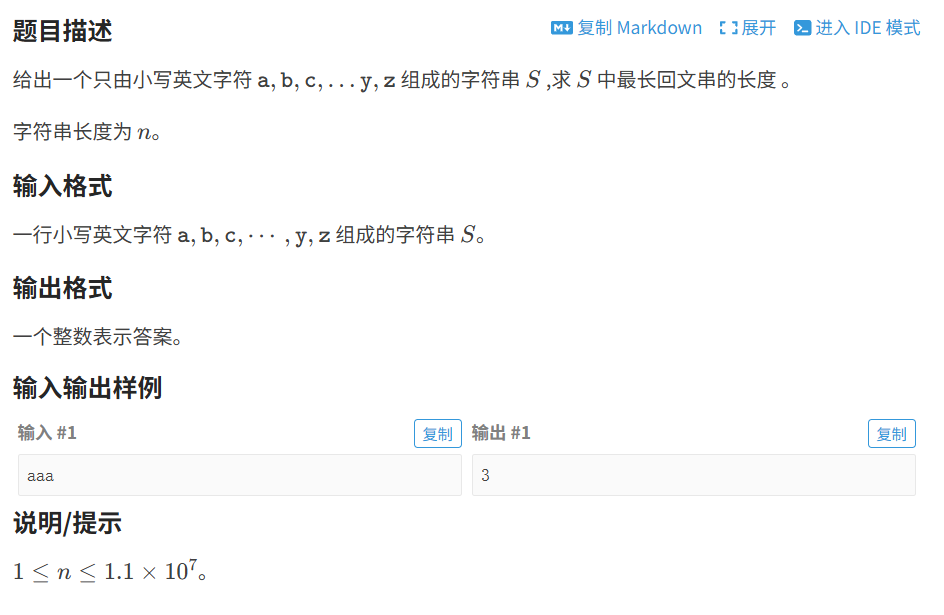
代码如下(示例):
c
#include <iostream>
using namespace std;
const int N = 2.2e7 + 10;
string t, s;
int m, n;
int d[N];
int main()
{
cin >> t; m = t.size();
s += ' ';
for (auto ch : t)
{
s += '#'; s += ch;
}
s += "##";
n = s.size() - 2;
d[1] = 1;
int ret = 1;
for (int i = 2, l = 1, r = 1; i <= n; i++)
{
int len = r >= i ? min(d[r - i + l], r - i + 1) : 1;
while (s[i + len] == s[i - len]) len++;
if (i + len - 1 > r) r = i + len - 1, l = i - len + 1;
d[i] = len;
ret = max(ret, d[i] - 1);
}
cout << ret << endl;
return 0;
}2.1 ABB
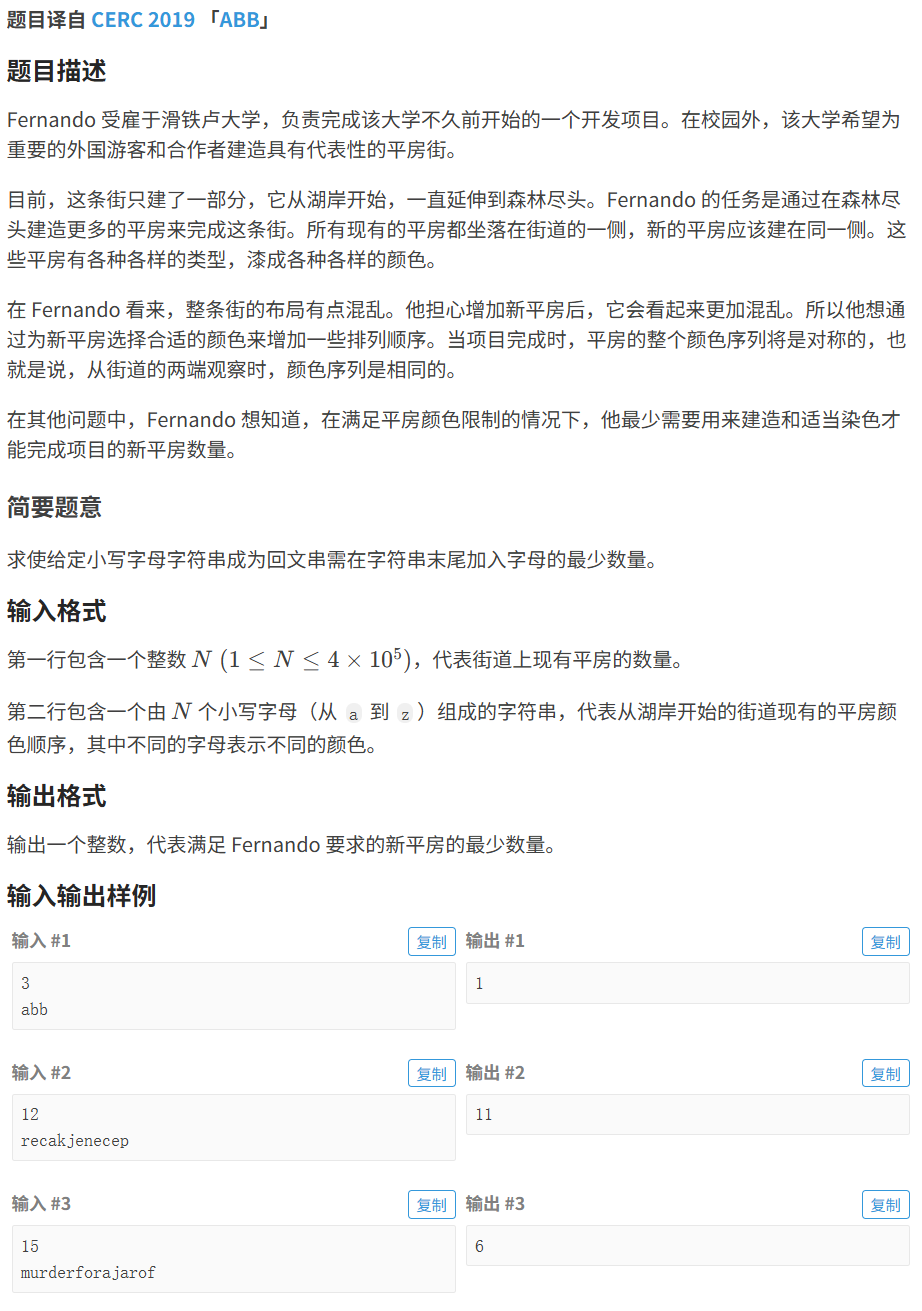


代码如下(示例):
c
#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int m, n;
string t, s;
int d[N];
int main()
{
cin >> m >> t;
s += ' ';
for (auto ch : t)
{
s += '#'; s += ch;
}
s += "##";
n = s.size() - 2;
int ret = 1;
d[1] = 1;
for (int i = 2, l = 1, r = 1; i <= n; i++)
{
int len = r >= i ? min(d[r - i + l], r - i + 1) : 1;
while (s[i + len] == s[i - len]) len++;
if (i + len - 1 > r) r = i + len - 1, l = i - len + 1;
d[i] = len;
if (i + d[i] - 1 == n) ret = max(ret, d[i] - 1);
}
cout << m - ret << endl;
return 0;
}2.2 ANT-Antisymmetry
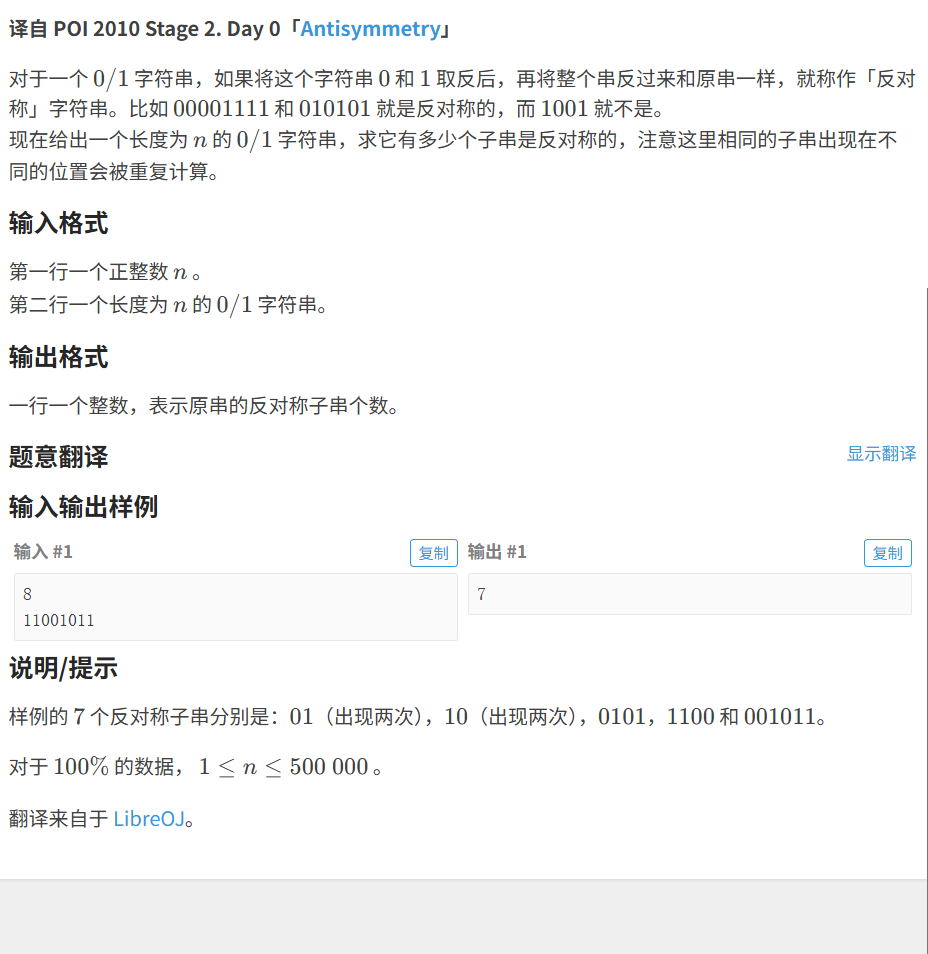



代码如下(示例):
c
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10;
int m, n;
string t, s;
int d[N];
bool check(int i, int j)
{
if (s[i] == '0' && s[j] == '1') return true;
else if (s[i] == '1' && s[j] == '0') return true;
else if (s[i] == '#' && s[i] == s[j]) return true;
return false;
}
int main()
{
cin >> m >> t;
s += ' ';
for (auto ch : t)
{
s += '#'; s += ch;
}
s += "##";
n = s.size() - 2;
d[1] = 1;
LL ret = 0;
for (int i = 3, l = 1, r = 1; i <= n; i += 2)
{
int len = r >= i ? min(d[r - i + l], r - i + 1) : 1;
while (check(i + len, i - len)) len++;
if (i + len - 1 > r) r = i + len - 1, l = i - len + 1;
d[i] = len;
ret = ret + d[i] / 2;
}
cout << ret << endl;
return 0;
}最后这两道题我实在是没时间解出了,贴个答案吧
2.3 拉拉队排练
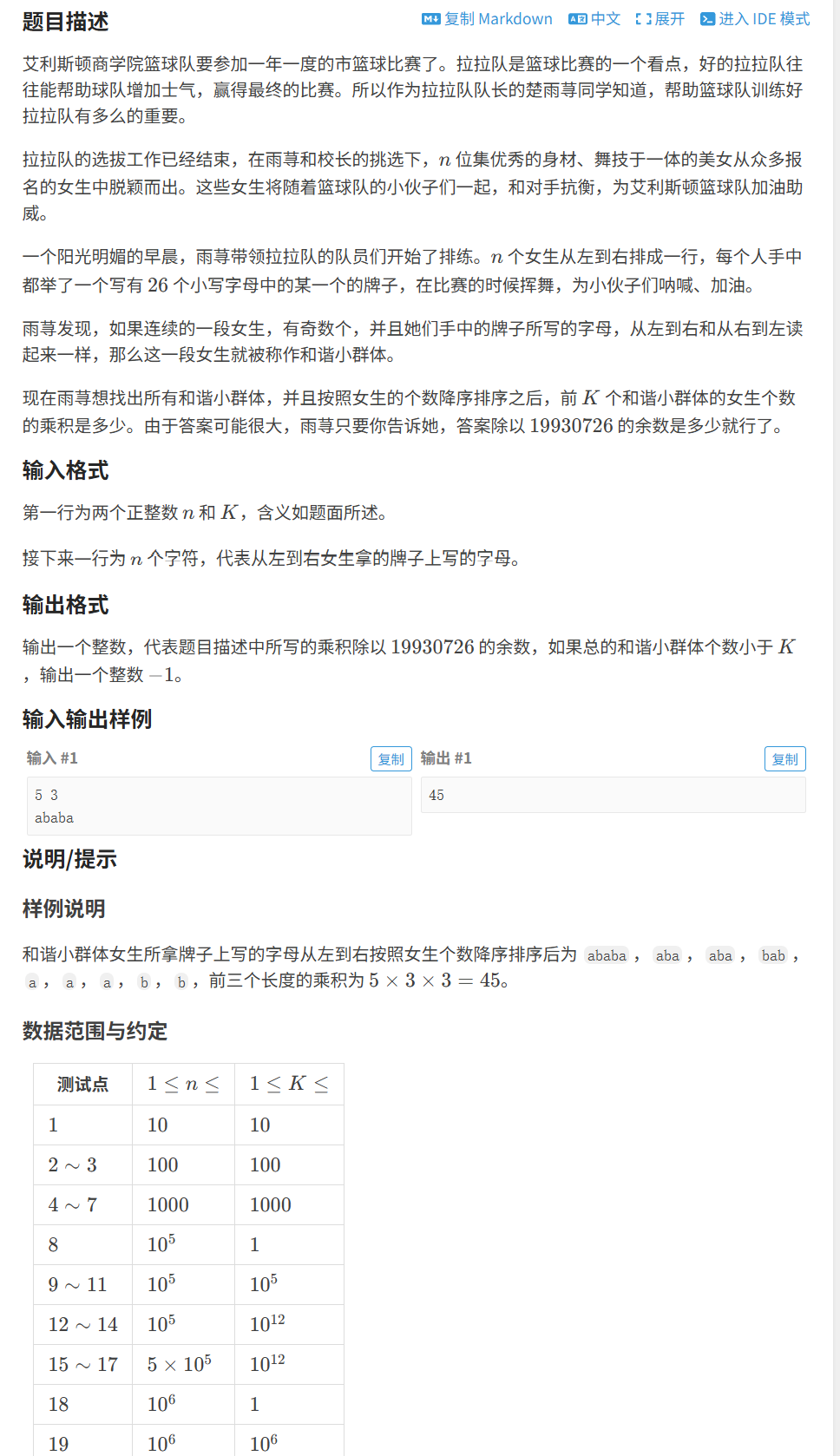

代码如下(示例):
c
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 2e6 + 10, mod = 19930726;
LL m, n, k;
string t, s;
LL d[N], cnt[N];
LL qpow(LL a, LL b, LL p)
{
LL ret = 1;
while (b)
{
if (b & 1) ret = ret * a % p;
a = a * a % p;
b >>= 1;
}
return ret;
}
int main()
{
cin >> m >> k >> t;
s += ' ';
for (auto ch : t)
{
s += '#'; s += ch;
}
s += "##";
n = s.size() - 2;
// manacher 算法
d[1] = 1;
for (int i = 2, l = 1, r = 1; i <= n; i++)
{
int len = r >= i ? min(d[r - i + l], r - i + 1ll) : 1;
while (s[i + len] == s[i - len]) len++;
if (i + len - 1 > r) r = i + len - 1, l = i - len + 1;
d[i] = len;
}
// 统计词频
for (int i = 2; i <= n; i += 2)
cnt[d[i] - 1]++;
// 统计结果
LL ret = 1, sum = 0;
for (int i = m / 2 * 2 + 1; i >= 1; i -= 2)
{
sum += cnt[i];
ret = ret * qpow(i, min(sum, k), mod) % mod;
k -= sum;
if (k <= 0) break;
}
if (k > 0) cout << -1 << endl;
else cout << ret << endl;
return 0;
}2.4 最⻓双回⽂串
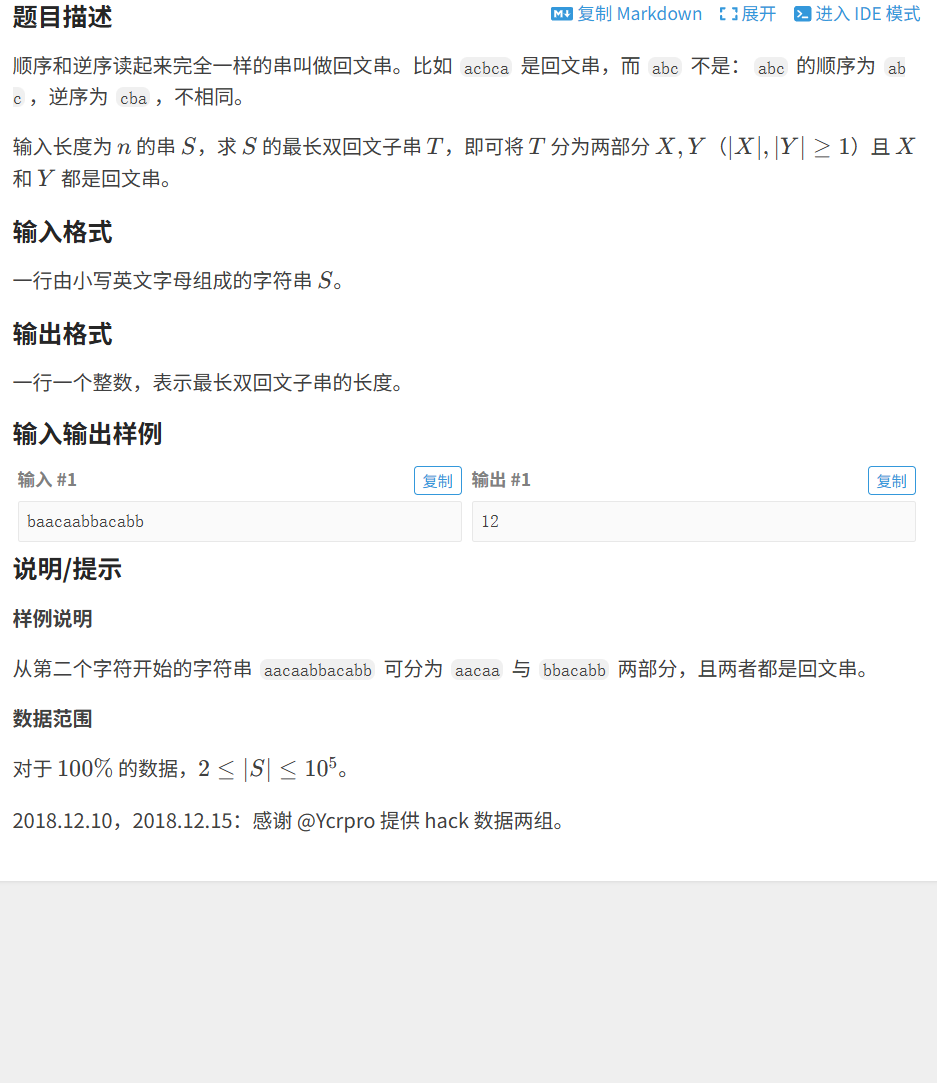

代码如下(示例):
c
#include <iostream>
using namespace std;
const int N = 2e5 + 10;
int m, n;
string t, s;
int d[N], l[N], r[N];
int main()
{
cin >> t; m = t.size();
s += ' ';
for (auto ch : t)
{
s += '#'; s += ch;
}
s += "##";
n = s.size() - 2;
d[1] = 1;
for (int i = 2, l = 1, r = 1; i <= n; i++)
{
int len = r >= i ? min(d[r - i + l], r - i + 1) : 1;
while (s[i + len] == s[i - len]) len++;
if (i + len - 1 > r) r = i + len - 1, l = i - len + 1;
d[i] = len;
}
for (int i = 1, j = 1; i <= n; i++)
{
while (j < i + d[i])
{
l[j] = j - i;
j += 2;
}
}
for (int i = n, j = n; i >= 1; i--)
{
while (j > i - d[i])
{
r[j] = i - j;
j -= 2;
}
}
int ret = 2;
for (int i = 3; i <= n - 2; i += 2)
ret = max(ret, r[i] + l[i]);
cout << ret << endl;
return 0;
}三、Leetcode里面算法题
入门
进阶
35. 回⽂⼦串(medium)

manacher 算法的 : 代码如下(示例):
c
class Solution {
static const int N = 4020;
int d[N];
public:
int countSubstrings(string s)
{
string t;
t += ' ';
for(auto ch : s)
{
t += '#';
t += ch;
}
t += "##";
int n = t.size() - 2;
int ans = 0;
d[1] = 1;
for(int i = 2 , l = 1 , r = 1 ; i <= n ; i++)
{
int len = r >= i ? min(d[r - i + l] , r - i + 1) : 1;
while(t[i + len] == t[i - len]) len++;
if(i + len - 1 > r) r = i + len - 1 , l = i - len + 1;
d[i] = len;
ans += d[i] / 2;
}
return ans;
}
};
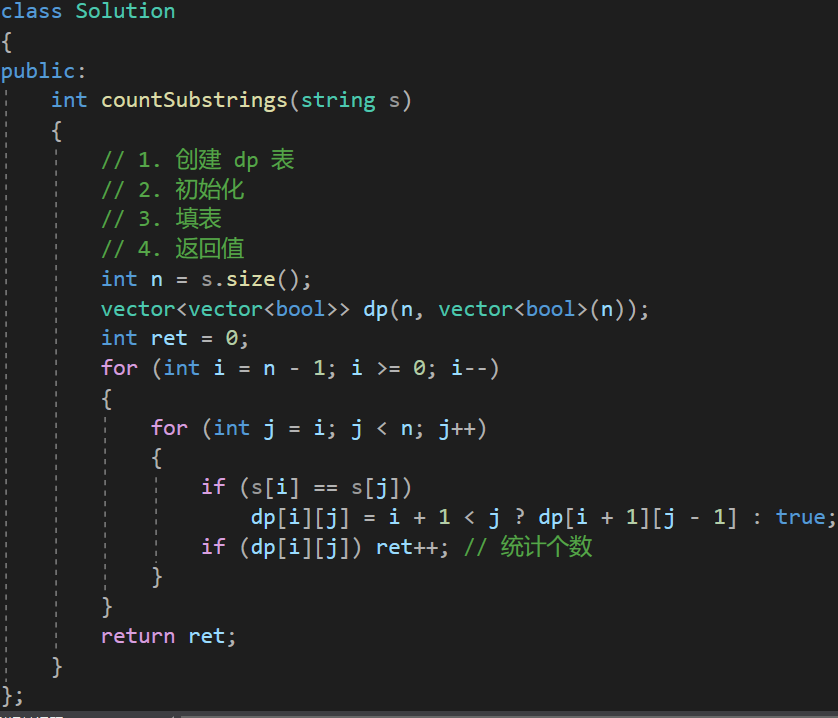
代码如下(示例):
c
class Solution
{
public:
int countSubstrings(string s)
{
// 1. 创建 dp 表
// 2. 初始化
// 3. 填表
// 4. 返回值
int n = s.size();
vector<vector<bool>> dp(n, vector<bool>(n));
int ret = 0;
for (int i = n - 1; i >= 0; i--)
{
for (int j = i; j < n; j++)
{
if (s[i] == s[j])
dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
if (dp[i][j]) ret++; // 统计个数
}
}
return ret;
}
};36. 最⻓回⽂⼦串(medium)

代码如下(示例):
c
// 中心扩展算法
class Solution {
public:
string longestPalindrome(string s)
{
int n = s.size() , left = 0 , right = 0 , len = 0 , begin = 0;
for(int i = 0 ; i < n ; i++)
{
// 处理奇数
left = i , right = i;
while(left >= 0 && right < n && s[left] == s[right])
{
left-- , right++;
}
if(right - left - 1 > len)
{
begin = left + 1;
len = right - left - 1;
}
// 处理偶数
left = i , right = i + 1;
while(left >= 0 && right < n && s[left] == s[right])
{
left-- , right++;
}
if(right - left - 1 > len)
{
begin = left + 1;
len = right - left - 1;
}
}
return s.substr(begin , len);
}
};
// manacher算法
class Solution {
private:
static const int N = 4020;
int d[N];
public:
string longestPalindrome(string s)
{
// 1. Manacher 预处理:统一奇偶回文
string t = " ";
for (char ch : s)
{
t += '#', t += ch;
}
t += "##";
int n = t.size() - 2;
// 2. Manacher 核心逻辑:找最长回文半径
int max_len = 1, max_pos = 1; // 最长半径、对应中心
d[1] = 1;
for (int i = 2, l = 1, r = 1; i <= n; i++)
{
// 初始化len:利用对称性优化
int len = r >= i ? min(d[r - i + l], r - i + 1) : 1;
// 扩展回文半径
while (t[i + len] == t[i - len]) len++;
// 更新最右回文边界
if (i + len - 1 > r) r = i + len - 1 , l = i - len + 1;
d[i] = len;
// 更新最长回文半径和中心
if (len > max_len)
{
max_len = len;
max_pos = i;
}
}
// 3. 还原原字符串的最长回文子串
int start = (max_pos - max_len) / 2; // 原串起始位置
int length = max_len - 1; // 原串最长回文长度
return s.substr(start, length);
}
};
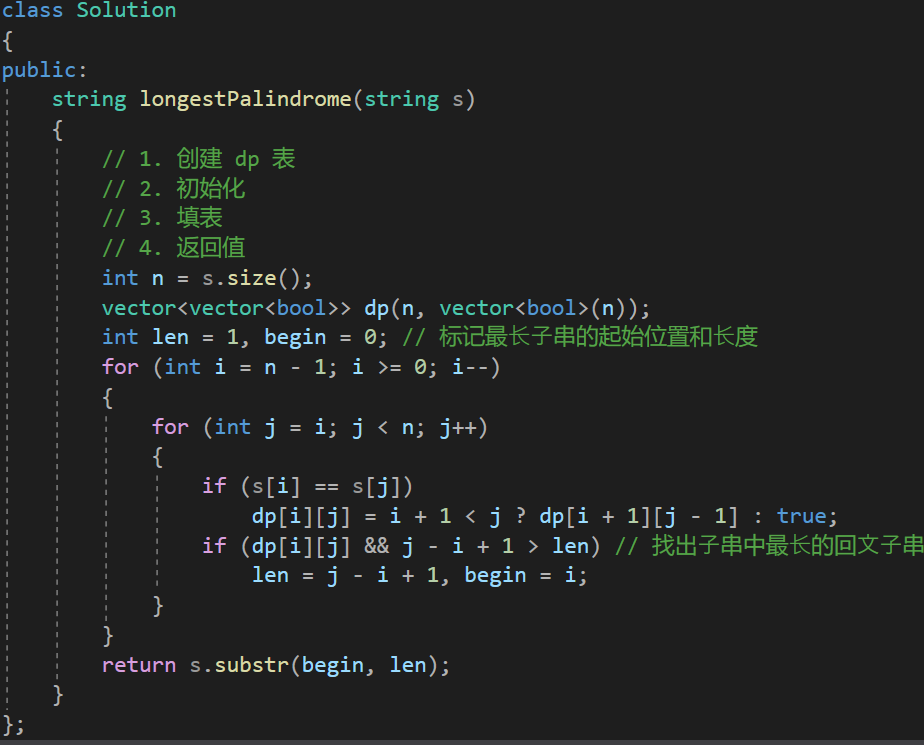
代码如下(示例):
c
class Solution
{
public:
string longestPalindrome(string s)
{
// 1. 创建 dp 表
// 2. 初始化
// 3. 填表
// 4. 返回值
int n = s.size();
vector<vector<bool>> dp(n, vector<bool>(n));
int len = 1, begin = 0; // 标记最⻓⼦串的起始位置和⻓度
for (int i = n - 1; i >= 0; i--)
{
for (int j = i; j < n; j++)
{
if (s[i] == s[j])
dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
if (dp[i][j] && j - i + 1 > len) // 找出⼦串中最⻓的回⽂⼦串
len = j - i + 1, begin = i;
}
}
return s.substr(begin, len);
}
};37. 回⽂串分割IV(hard)

manacher算法如下
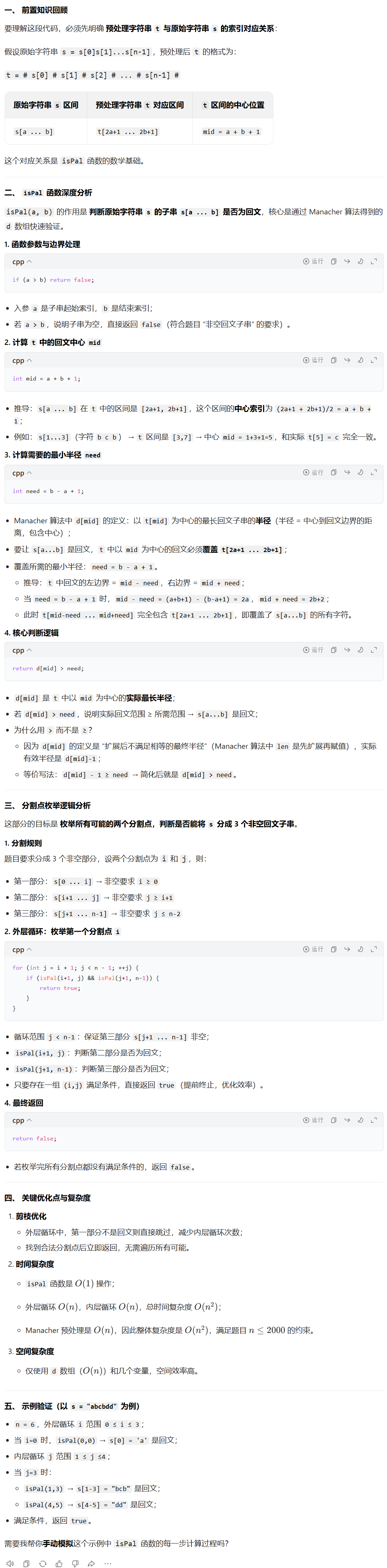
代码如下(示例):
c
class Solution {
static const int N = 4020;
int d[N];
public:
bool checkPartitioning(string s)
{
int n = s.size();
if (n < 3) return false;
// 步骤1:预处理字符串 t,格式 #s0#s1#...#sn-1#
string t;
for (char ch : s)
{
t += '#';
t += ch;
}
t += '#';
int m = t.size();
// 步骤2:Manacher 算法计算 d 数组
int l = 1, r = 1;
for (int i = 0; i < m; i++)
{
// 初始化半径
int len = (i > r) ? 1 : min(d[l + r - i], r - i + 1);
// 扩展半径 + 越界防护
while (i - len >= 0 && i + len < m && t[i - len] == t[i + len]) len++;
// 更新最右边界
if (i + len - 1 > r) r = i + len - 1 , l = i - len + 1;
d[i] = len;
}
// 步骤3:正确的回文判断函数
auto isPal = [&](int a, int b)
{
if (a > b) return false;
int mid = a + b + 1; // t 中的中心索引
int need = b - a + 1; // 需要的半径
return d[mid] - 1 >= need;
};
// 步骤4:枚举分割点(分成 3 个非空回文子串)
for (int i = 0; i < n - 2; ++i)
{
if (!isPal(0, i)) continue; // 第一部分 s[0..i]
for (int j = i + 1; j < n - 1; j++)
{
// 第二部分 s[i+1..j],第三部分 s[j+1..n-1]
if (isPal(i+1, j) && isPal(j+1, n-1))
{
return true;
}
}
}
return false;
}
};
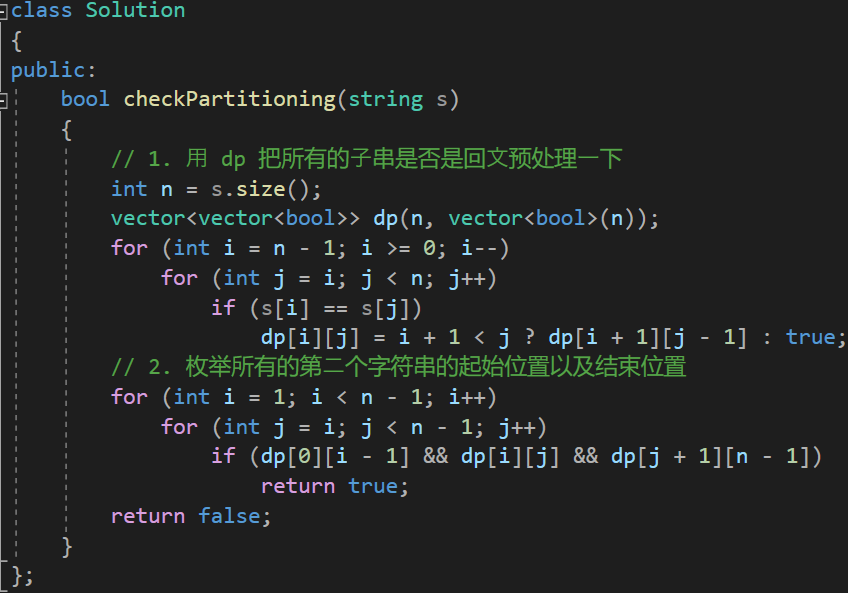
代码如下(示例):
c
class Solution
{
public:
bool checkPartitioning(string s)
{
// 1. ⽤ dp 把所有的⼦串是否是回⽂预处理⼀下
int n = s.size();
vector<vector<bool>> dp(n, vector<bool>(n));
for (int i = n - 1; i >= 0; i--)
for (int j = i; j < n; j++)
if (s[i] == s[j])
dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;
// 2. 枚举所有的第⼆个字符串的起始位置以及结束位置
for (int i = 1; i < n - 1; i++)
for (int j = i; j < n - 1; j++)
if (dp[0][i - 1] && dp[i][j] && dp[j + 1][n - 1])
return true;
return false;
}
};38. 分割回⽂串II(hard)

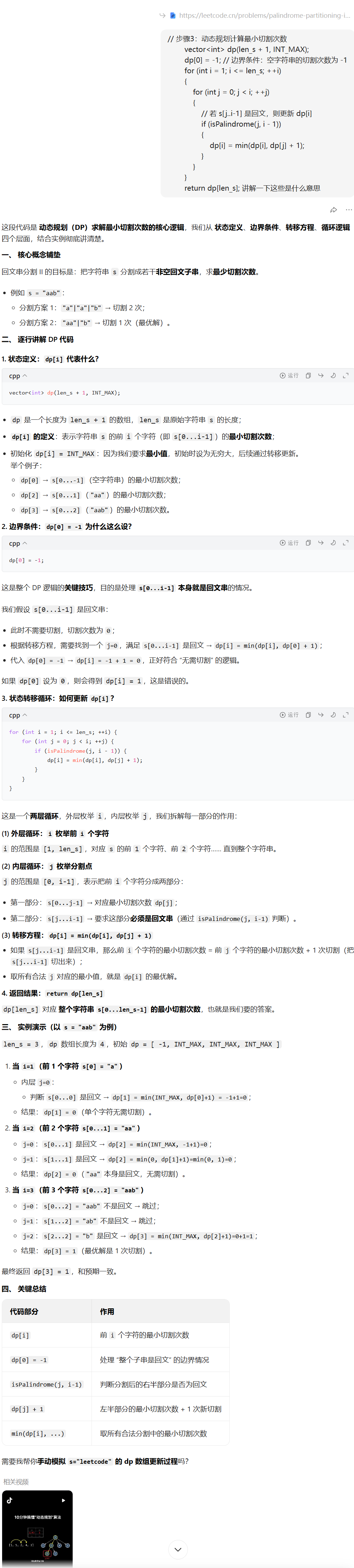
代码如下(示例):
c
// manache算法
class Solution {
public:
int minCut(string s)
{
int len_s = s.size();
if (len_s <= 1) return 0;
// 步骤1:Manacher 算法预处理,生成半径数组 d
string t;
for (char ch : s)
{
t += '#';
t += ch;
}
t += '#';
int len_t = t.size();
vector<int> d(len_t, 0); // 改用动态数组,避免固定大小限制
int l = 1, r = 1;
for (int i = 0; i < len_t; i++)
{
// 初始化半径
int len = (i > r) ? 1 : min(d[l + r - i], r - i + 1);
// 扩展半径,防止越界
while (i - len >= 0 && i + len < len_t && t[i - len] == t[i + len]) len++;
d[i] = len;
// 更新最右回文边界
if (i + len - 1 > r) l = i - len + 1 , r = i + len - 1;
}
// 步骤2:快速判断 s[a...b] 是否为回文的辅助函数
auto isPalindrome = [&](int a, int b)
{
if (a > b) return false;
int mid = a + b + 1; // 对应 t 的中心索引
int need = b - a + 1; // 需要的最小有效半径
return (d[mid] - 1) >= need;
};
// 步骤3:动态规划计算最小切割次数
vector<int> dp(len_s + 1, INT_MAX);
dp[0] = -1; // 边界条件:空字符串的切割次数为 -1
for (int i = 1; i <= len_s; ++i)
{
for (int j = 0; j < i; ++j)
{
// 若 s[j..i-1] 是回文,则更新 dp[i]
if (isPalindrome(j, i - 1))
{
dp[i] = min(dp[i], dp[j] + 1);
}
}
}
return dp[len_s];
}
};

代码如下(示例):
c
class Solution {
public:
int minCut(string s)
{
int n = s.size();
vector<vector<bool>> isPal(n, vector<bool>(n)); // 统计所有⼦串是否是回⽂串
for (int i = n - 1; i >= 0; i--)
for (int j = i; j < n; j++)
isPal[i][j] = s[i] == s[j] ? (i + 1 < j ? isPal[i + 1][j - 1]
: true) : false;
vector<int> dp(n, INT_MAX);
for (int i = 0; i < n; i++)
{
if (isPal[0][i]) dp[i] = 0;
else
{
for (int j = 1; j <= i; j++)
if (isPal[j][i])
dp[i] = min(dp[i], dp[j - 1] + 1);
}
}
return dp[n - 1];
}
};39. 最⻓回⽂⼦序列(medium)



代码如下(示例):
c
class Solution
{
public:
int longestPalindromeSubseq(string s)
{
int n = s.size();
vector<vector<int>> dp(n, vector<int>(n)); // 搞⼀个 dp 表
for (int i = n - 1; i >= 0; i--) // 枚举左端点 i
{
dp[i][i] = 1; // 填表的时候初始化
for (int j = i + 1; j < n; j++) // 然后从 i + 1 的位置枚举右端点
{
// 分两种情况填写 dp 表
if (s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1] + 2;
else dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}
}
// 返回结果
return dp[0][n - 1];
}
};40. 让字符串成为回⽂串的最⼩插⼊次数(hard)


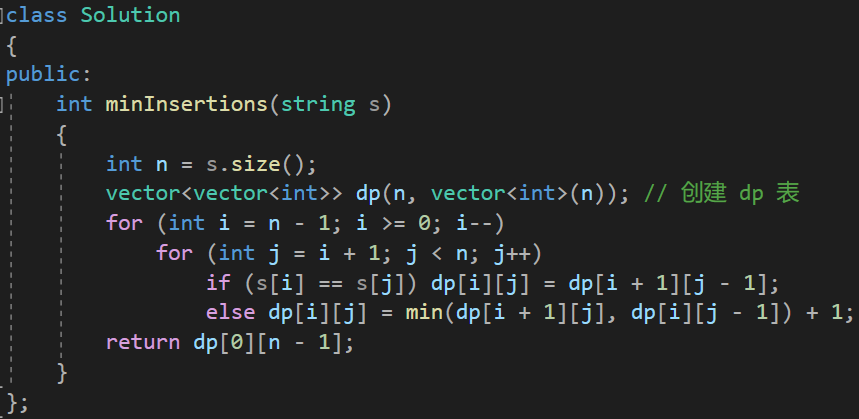
代码如下(示例):
c
class Solution
{
public:
int minInsertions(string s)
{
int n = s.size();
vector<vector<int>> dp(n, vector<int>(n)); // 创建 dp 表
for (int i = n - 1; i >= 0; i--)
for (int j = i + 1; j < n; j++)
if (s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1];
else dp[i][j] = min(dp[i + 1][j], dp[i][j - 1]) + 1;
return dp[0][n - 1];
}
};总结
这篇文章是作者搜集大量面经和资料这里出来的。感谢你的支持
作者wkm是一名中国矿业大学(北京) 大一的新生,希望得到你的关注
如果可以的话,记得一键三联!