从链式法则的数学本质出发,彻底揭开神经网络训练崩溃的真相,并掌握5大核心解决方案。
1 祸起萧墙:链式法则与连乘效应
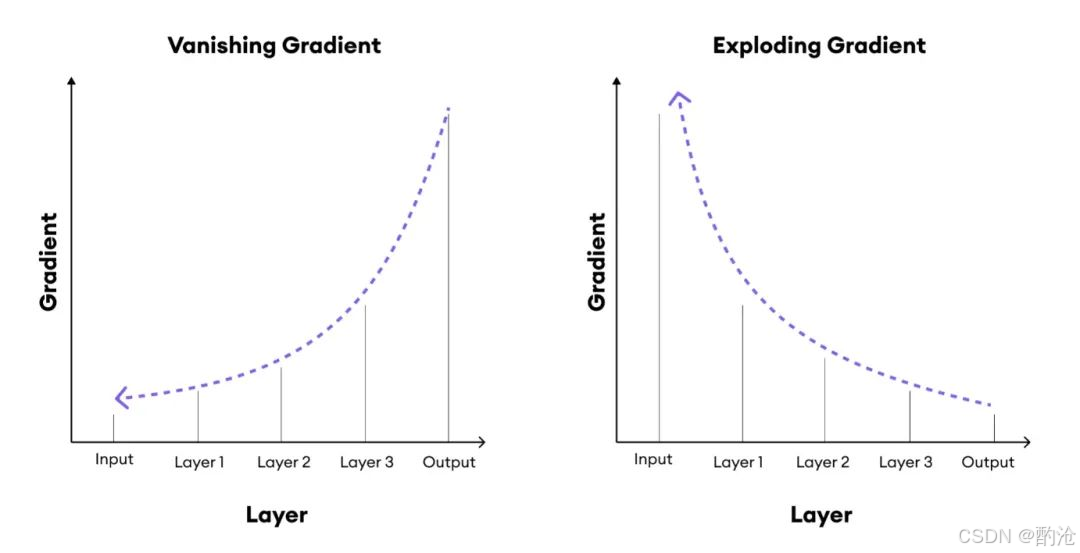
反向传播是深度学习的基石,但它也是导致梯度消失 和梯度爆炸的根本原因。
1.1 极简模型推演
为了直观理解,我们剥离复杂的网络结构,构建一个只有 3 层隐藏层的单一直线网络,且忽略偏置项 bbb:

前向传播公式 :hi=σ(wi⋅hi−1)h_i = \sigma(w_i \cdot h_{i-1})hi=σ(wi⋅hi−1),其中 σ\sigmaσ 为激活函数。
目标 :我们要更新第一层的权重 w1w_1w1,需要计算损失函数 LLL 对 w1w_1w1 的导数。
根据链式法则 ,梯度是从后往前传递的连乘积。梯度的表达式是一串形如 (w⋅σ′)(w \cdot \sigma')(w⋅σ′) 的因子乘积。
1.2 梯度消失:无声的死机
这是深层网络最常见的问题。
数学诱因 :假设使用经典的Sigmoid激活函数,其导数 σ′(z)\sigma'(z)σ′(z) 的最大值仅为0.25
数值模拟 :若初始化权重 w=1.0w=1.0w=1.0,且层数较多。梯度∝0.25×0.25×0.25... \text{梯度} \propto 0.25 \times 0.25 \times 0.25 \dots 梯度∝0.25×0.25×0.25... 3层网络梯度衰减为原来的1/64,50层网络 0.2550≈10−300.25^{50} \approx 10^{-30}0.2550≈10−30
后果:靠近输入的层(底层)几乎接收不到梯度信号,参数无法更新,网络前端瘫痪,无法提取底层特征。
1.3 梯度爆炸:疯狂的震荡
相对少见,但在 RNN 或初始化不当时容易发生。
数学诱因 :假设权重初始化过大(如 w=10w=10w=10),且激活函数导数较大。
数值模拟 :梯度∝10×10×10... \text{梯度} \propto 10 \times 10 \times 10 \dots 梯度∝10×10×10... 50层网络 105010^{50}1050 这是一个天文数字。
后果:权重更新步幅过大,直接跨过最优解,导致 Loss 值震荡甚至变成NaN(Not a Number),模型瞬间崩溃。
2 破局之道:五大核心解决方案
针对上述数学本质,工业界已经总结出了一套成熟的组合拳。
2.1 换芯:ReLU 激活函数
这是解决梯度消失最直接、最有效的方法,也是现代深度学习的标配。
原理 :f(x)=max(0,x)f(x) = \max(0, x)f(x)=max(0,x)。当 x>0x>0x>0 时,其导数恒为 1。
优势 :1×1×⋯=11 \times 1 \times \dots = 11×1×⋯=1。无论网络多深,只要神经元被激活,梯度就能无损地传回底层,彻底打破了 Sigmoid 的0.25 诅咒。
2.2 归一:Batch Normalization (BN)
BN 是深度学习中的神技,能同时缓解消失和爆炸。
原理:在激活函数之前,强行将神经元输入的分布拉回到均值为 0、方差为 1 的标准正态分布。
作用:1. 将输入拉回激活函数的非饱和区(敏感区),保证导数不为 0。 2. 规范了权重的尺度,防止连乘导致的数值剧烈波动。
2.3 抄近道:残差结构 (ResNet)
ResNet 的提出让千层网络的训练成为可能。
原理 :引入Skip Connection,公式变为 y=f(x)+xy = f(x) + xy=f(x)+x。
数学本质 :求导时 ∂y∂x=∂f∂x+1\frac{\partial y}{\partial x} = \frac{\partial f}{\partial x} + \mathbf{1}∂x∂y=∂x∂f+1。
作用 :这个 +1 建立了一条梯度的高速公路。即使深层 f(x)f(x)f(x) 的梯度趋近于 0,梯度依然可以通过恒等映射(Identity Mapping)无损传到底层。
2.4 预备:合理的权重初始化
好的开始是成功的一半。
Xavier 初始化:适用于 Sigmoid/Tanh。保持输入输出方差一致。
He 初始化 (Kaiming Init):适用于 ReLU。针对 ReLU 的特性调整方差,是目前的最佳实践。
| 特性 | Xavier (Glorot) | He (Kaiming) |
|---|---|---|
| 最佳拍档 | Sigmoid / Tanh | ReLU / Leaky ReLU |
| 类比 | 普通传声筒:假设声音无损传输,只管两头对齐。 | 增强传声筒 :因为中间有损耗(ReLU 过滤了一半声音),所以必须在源头把声音放大一倍。 |
| 如果不匹配 | 用在 ReLU 上会导致信号越来越弱(梯度消失)。 | 用在 Sigmoid 上会导致信号过强,进入饱和区(梯度消失)。 |
2.5 熔断:梯度裁剪
专门针对梯度爆炸的防御机制,常用于 RNN/LSTM。
做法:在更新参数前检测梯度的范数(Norm)。若超过阈值(如 5.0),则强行按比例缩小梯度。
专门针对梯度爆炸的防御机制,常用于 RNN/LSTM。
做法:在更新参数前检测梯度的范数(Norm)。若超过阈值(如 5.0),则强行按比例缩小梯度。
作用:物理层面的限速,防止参数更新步子迈得太大飞出可行域。