SmoothQuant：一种用于大型语言模型的准确高效的训练后量化方法

1.问题背景与核心思想

LLMs量化的主要难点：激活值(activations)中存在持续性的异常值(outliers)，使得激活值难以精确量化 。虽然per-channel activation quantization（每个通道独立量化）可以有效解决这个问题，但它无法在硬件上高效实现，因为硬件加速的GEMM内核要求缩放只能沿矩阵乘法的外维度进行（即激活的token维度T和权重的输出通道维度Co）。

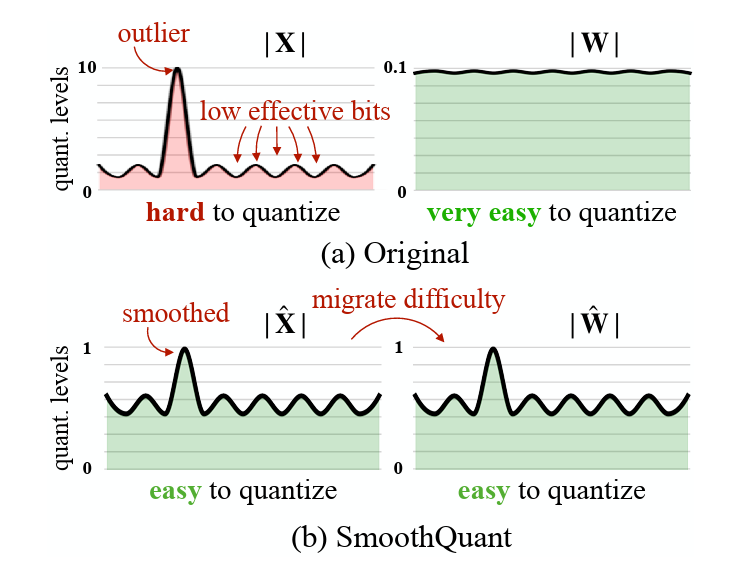
SmoothQuant的核心创新在于：通过一个数学等价的变换，将量化难度从激活值迁移到权重上 。如下图所示，平滑前的激活值X因为异常值的存在难以量化（量化范围被拉伸，导致大部分值只用了很少的有效比特位），而权重WWW则相对容易量化。通过离线的变换，SmoothQuant可以将这种难度分布重新平衡，使得X̂和Ŵ都变得容易量化。

2. 数学形式化

2.1. 基本变换公式

考虑一个线性层的计算： Y=X⋅WY = X·WY=X⋅W

SmoothQuant引入一个per-channel的平滑因子 s∈RCis∈R^{C_i}s∈RCi

对输入进行变换：
Y=(X⋅diag(s)−1)⋅(diag(s)⋅W)=X^⋅W^(3)Y = (X·diag(s)^{-1})·(diag(s)·W) = X̂·Ŵ (3)Y=(X⋅diag(s)−1)⋅(diag(s)⋅W)=X^⋅W^(3)

其中：

X^=X⋅diag(s)−1X̂ = X·diag(s)^{-1}X^=X⋅diag(s)−1是平滑后的激活
$Ŵ = diag(s)\cdotW$ 是调整后的权重

这个变换是数学等价的，不会改变模型的输出。重要的是，这个变换可以离线完成，不会引入额外的运行时开销。对于前面线性操作产生的输入X，我们可以将平滑因子融合到前一层的参数中

2.2 平滑因子的选择

首先考虑一个直观的选择： sj=max(∣Xj∣)s_j = max(|X_j|)sj=max(∣Xj∣)

其中 jjj表示第 jjj个输入通道。这样可以使所有通道在平滑后具有相同的最大值，便于量化。然而，这种方法将全部量化难度转移到了权重上，导致较大的精度损失。

为了平衡激活和权重的量化难度，论文引入了迁移强度参数α：
sj=max(∣Xj∣)α/max(∣Wj∣)(1−α)(4)s_j = max(|X_j|)^α / max(|W_j|)^{(1-α) } (4)sj=max(∣Xj∣)α/max(∣Wj∣)(1−α)(4)

当α=0时，所有量化难度都在权重上
当α=1时，所有量化难度都在激活上
当α=0.5时，量化难度在权重和激活之间均匀分配（适用于OPT、BLOOM等模型）
对于GLM-130B等激活异常值更显著的模型，需要更大的α（如0.75）将更多难度迁移到权重

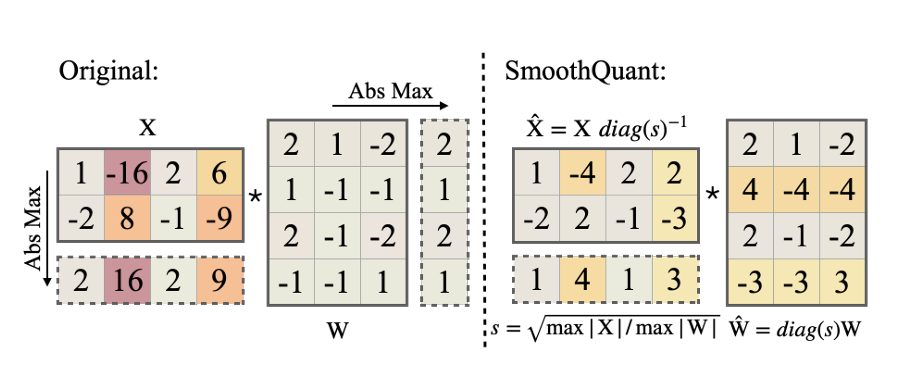
2.3. Transformer模块中的实现

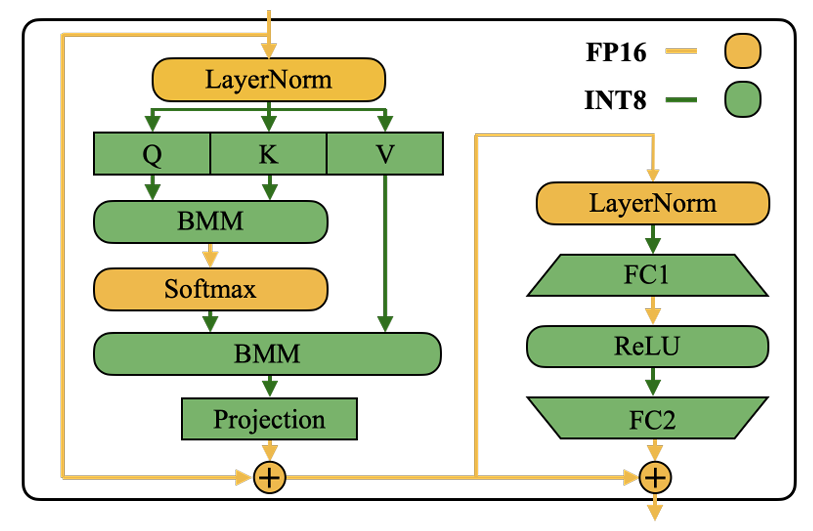
上图详细展示了SmoothQuant在Transformer block中的精度分配：

自注意力机制：

Q、K、V投影：W8A8量化（输入激活平滑，权重调整）
注意力分数计算：K和Q的BMM（Batch Matrix Multiplication）使用INT8
注意力输出投影：W8A8量化

前馈网络：

第一层线性变换：W8A8量化
第二层线性变换：W8A8量化

其他操作：

Softmax、LayerNorm等轻量级逐元素操作保持FP16
残差连接保持FP16

这种设计平衡了精度和效率，将INT8算术用于计算密集型操作，而将FP16保留给对量化敏感的轻量级操作。

2.4 平滑效果可视化

上图展示了SmoothQuant应用前后的效果对比：

左侧：原始激活值包含少数幅度很大的通道（>70），形成明显的异常值；而权重分布相对均匀平坦
右侧：应用SmoothQuant后，激活值中的异常值被大幅平滑，所有通道的幅度变得相对均衡；权重虽然引入了一些变化，但整体仍然保持较为均匀的分布

这一可视化验证了SmoothQuant的核心思想：通过离线的数学等价变换，将激活中的异常值影响迁移到权重上，使两者都变得适合INT8量化。

3.完整示例

假设我们有一个线性层： Y=X⋅WY = X \cdot WY=X⋅W，其中 XXX是输入激活(维度 T×CiT \times C_iT×Ci)， WWW是权重(维度 Ci×CoC_i \times C_oCi×Co)， YYY是输出(维度 T×CoT \times C_oT×Co)。

步骤1：观察原始激活和权重的数据分布

考虑以下简化例子：

当然可以。以下是使用 LaTeX 语法表示的矩阵形式：

输入激活XXX(2 个 token，4 个通道）：

X=[1.02.0100.03.00.51.0150.02.0]X = \begin{bmatrix} 1.0 & 2.0 & 100.0 & 3.0 \\ 0.5 & 1.0 & 150.0 & 2.0 \end{bmatrix} X=[1.00.52.01.0100.0150.03.02.0]

权重 $W$ （4 个输入通道，3 个输出通道）：
W=[0.10.20.30.20.10.40.010.020.030.30.20.1] W = \begin{bmatrix} 0.1 & 0.2 & 0.3 \\ 0.2 & 0.1 & 0.4 \\ 0.01 & 0.02 & 0.03 \\ 0.3 & 0.2 & 0.1 \end{bmatrix} W= 0.10.20.010.30.20.10.020.20.30.40.030.1

观察：第3个通道(索引2)的激活值(100.0和150.0)远远大于其他通道，形成了明显的异常值。如果直接量化，这些异常值会主导量化范围，导致其他通道精度严重损失。

步骤2：计算平滑因子sss

平滑因子公式：
sj=max⁡(∣Xj∣)αmax⁡(∣Wj∣)1−αs_j = \frac{\max(|X_j|)^\alpha}{\max(|W_j|)^{1-\alpha}}sj=max(∣Wj∣)1−αmax(∣Xj∣)α

计算每个通道的最大绝对值：

激活 XXX各通道最大值：[1.0,2.0,150.0,3.0][1.0, 2.0, 150.0, 3.0][1.0,2.0,150.0,3.0]
权重 WWW各通道最大值：[0.3,0.4,0.03,0.3][0.3, 0.4, 0.03, 0.3][0.3,0.4,0.03,0.3]

选择迁移强度 α\alphaα：

对于大多数模型， α=0.5\alpha=0.5α=0.5是平衡点
对于异常值更严重的模型(如GLM-130B)，可能需要α=0.75\alpha=0.75α=0.75

计算平滑因子 (设 α=0.5\alpha=0.5α=0.5)：
s0=1.00.3≈1.83 s_0 = \sqrt{\frac{1.0}{0.3}} \approx 1.83 s0=0.31.0 ≈1.83
s1=2.00.4≈2.24s_1 = \sqrt{\frac{2.0}{0.4}} \approx 2.24 s1=0.42.0 ≈2.24
s2=150.00.03≈70.71s_2 = \sqrt{\frac{150.0}{0.03}} \approx 70.71 s2=0.03150.0 ≈70.71
s3=3.00.3≈3.16s_3 = \sqrt{\frac{3.0}{0.3}} \approx 3.16s3=0.33.0 ≈3.16
s=[1.83,2.24,70.71,3.16]s = [1.83, 2.24, 70.71, 3.16] s=[1.83,2.24,70.71,3.16]

注意：在实际实现中， max⁡(∣Xj∣)\max(|X_j|)max(∣Xj∣)是通过校准数据集(如Pile数据集的512个样本)统计得到的。

步骤3：应用平滑变换

执行数学等价变换：
Y=X⋅W=(X⋅diag(s)−1)⋅(diag(s)⋅W)=X^⋅W^Y = X \cdot W = (X \cdot \text{diag}(s)^{-1}) \cdot (\text{diag}(s) \cdot W) = \hat{X} \cdot \hat{W}Y=X⋅W=(X⋅diag(s)−1)⋅(diag(s)⋅W)=X^⋅W^

平滑激活 XXX：
X^=[1.01.832.02.24100.070.713.03.160.51.831.02.24150.070.712.03.16]\hat{X} = \begin{bmatrix} \frac{1.0}{1.83} & \frac{2.0}{2.24} & \frac{100.0}{70.71} & \frac{3.0}{3.16} \\ \frac{0.5}{1.83} & \frac{1.0}{2.24} & \frac{150.0}{70.71} & \frac{2.0}{3.16} \end{bmatrix}X^=[1.831.01.830.52.242.02.241.070.71100.070.71150.03.163.03.162.0]
≈[0.550.891.410.950.270.452.120.63] \approx \begin{bmatrix} 0.55 & 0.89 & 1.41 & 0.95 \\ 0.27 & 0.45 & 2.12 & 0.63 \end{bmatrix}≈[0.550.270.890.451.412.120.950.63]
调整权重 WWW：
W^=[1.83×0.11.83×0.21.83×0.32.24×0.22.24×0.12.24×0.470.71×0.0170.71×0.0270.71×0.033.16×0.33.16×0.23.16×0.1]\hat{W} = \begin{bmatrix} 1.83 \times 0.1 & 1.83 \times 0.2 & 1.83 \times 0.3 \\ 2.24 \times 0.2 & 2.24 \times 0.1 & 2.24 \times 0.4 \\ 70.71 \times 0.01 & 70.71 \times 0.02 & 70.71 \times 0.03 \\ 3.16 \times 0.3 & 3.16 \times 0.2 & 3.16 \times 0.1 \end{bmatrix} W^= 1.83×0.12.24×0.270.71×0.013.16×0.31.83×0.22.24×0.170.71×0.023.16×0.21.83×0.32.24×0.470.71×0.033.16×0.1
≈[0.180.370.550.450.220.900.711.412.120.950.630.32]\approx \begin{bmatrix} 0.18 & 0.37 & 0.55 \\ 0.45 & 0.22 & 0.90 \\ 0.71 & 1.41 & 2.12 \\ 0.95 & 0.63 & 0.32 \end{bmatrix}≈ 0.180.450.710.950.370.221.410.630.550.902.120.32
验证数学等价性：

原始计算
KaTeX parse error: Expected 'EOF', got '&' at position 231: ...n{bmatrix} 2.0 &̲ 3.0 & 4.4 \\ 2...

SmoothQuant变换后计算
Y^=X^⋅W^=[0.550.891.410.950.270.452.120.63]⋅[0.180.370.550.450.220.900.711.412.120.950.630.32]≈[2.003.014.412.264.015.66]\hat{Y} = \hat{X} \cdot \hat{W} = \begin{bmatrix} 0.55 & 0.89 & 1.41 & 0.95 \\ 0.27 & 0.45 & 2.12 & 0.63 \end{bmatrix} \cdot \begin{bmatrix} 0.18 & 0.37 & 0.55 \\ 0.45 & 0.22 & 0.90 \\ 0.71 & 1.41 & 2.12 \\ 0.95 & 0.63 & 0.32 \end{bmatrix} \approx \begin{bmatrix} 2.00 & 3.01 & 4.41 \\ 2.26 & 4.01 & 5.66 \end{bmatrix}Y^=X^⋅W^=[0.550.270.890.451.412.120.950.63]⋅ 0.180.450.710.950.370.221.410.630.550.902.120.32 ≈[2.002.263.014.014.415.66]

两者的输出基本一致（微小差异来自四舍五入误差），验证了变换的数学等价性。

步骤4：融合平滑操作（实际部署优化）

在实际实现中，平滑操作会被融合到前一层：

如果 XXX来自线性层，将平滑因子融合到前一层权重
如果 XXX来自LayerNorm，将平滑因子融合到LayerNorm的缩放参数
如果 XXX来自残差连接，对残差分支添加额外缩放

这样在推理时无需额外的计算操作，避免了性能开销。例如，如果 X=Z⋅VX = Z \cdot VX=Z⋅V，其中 ZZZ是前一层的输出， VVV是前一层的权重，则：
Y=X⋅W=(Z⋅V)⋅WY = X \cdot W = (Z \cdot V) \cdot W Y=X⋅W=(Z⋅V)⋅W
=Z⋅(V⋅diag(s)−1)⋅(diag(s)⋅W)= Z \cdot (V \cdot \text{diag}(s)^{-1}) \cdot (\text{diag}(s) \cdot W) =Z⋅(V⋅diag(s)−1)⋅(diag(s)⋅W)
=Z⋅V^⋅W^= Z \cdot \hat{V} \cdot \hat{W}=Z⋅V^⋅W^

其中 V^=V⋅diag(s)−1\hat{V} = V \cdot \text{diag}(s)^{-1}V^=V⋅diag(s)−1可以预先计算并替换原始权重 VVV。

步骤5：量化平滑后的数据

现在对平滑后的 X^\hat{X}X^和 W^\hat{W}W^进行INT8量化：

计算量化参数：

量化公式： Xˉ=round(X^ΔX^)\bar{X} = \text{round}\left(\frac{\hat{X}}{\Delta_{\hat{X}}}\right)Xˉ=round(ΔX^X^)，Wˉ=round(W^ΔW^)\bar{W} = \text{round}\left(\frac{\hat{W}}{\Delta_{\hat{W}}}\right)Wˉ=round(ΔW^W^)
量化步长： Δ=max⁡(∣X∣)2N−1−1\Delta = \frac{\max(|X|)}{2^{N-1}-1}Δ=2N−1−1max(∣X∣)，其中N=8N=8N=8
X^\hat{X}X^的最大绝对值 = 2.12，量化步长 ΔX^=2.12127≈0.0167\Delta_{\hat{X}} = \frac{2.12}{127} \approx 0.0167ΔX^=1272.12≈0.0167
W^\hat{W}W^的最大绝对值 = 2.12，量化步长 ΔW^=2.12127≈0.0167\Delta_{\hat{W}} = \frac{2.12}{127} \approx 0.0167ΔW^=1272.12≈0.0167

执行量化（四舍五入到最近整数）：

Xˉ=round(X^0.0167)\bar{X} = \text{round}\left(\frac{\hat{X}}{0.0167}\right)Xˉ=round(0.0167X^)

=round([0.550.01670.890.01671.410.01670.950.01670.270.01670.450.01672.120.01670.630.0167])= \text{round}\left(\left[\begin{array}{cccc} \frac{0.55}{0.0167} & \frac{0.89}{0.0167} & \frac{1.41}{0.0167} & \frac{0.95}{0.0167} \\ \frac{0.27}{0.0167} & \frac{0.45}{0.0167} & \frac{2.12}{0.0167} & \frac{0.63}{0.0167} \end{array}\right]\right)=round([0.01670.550.01670.270.01670.890.01670.450.01671.410.01672.120.01670.950.01670.63])

=round([32.9353.2984.4356.8916.1726.95126.9537.72])= \text{round}\left(\left[\begin{array}{cccc} 32.93 & 53.29 & 84.43 & 56.89 \\ 16.17 & 26.95 & 126.95 & 37.72 \end{array}\right]\right)=round([32.9316.1753.2926.9584.43126.9556.8937.72])

≈[33538457162712738]\approx \left[\begin{array}{cccc} 33 & 53 & 84 & 57 \\ 16 & 27 & 127 & 38 \end{array}\right]≈[33165327841275738]

Wˉ=round(W^0.0167)\bar{W} = \text{round}\left(\frac{\hat{W}}{0.0167}\right)Wˉ=round(0.0167W^)

=round([0.180.01670.370.01670.550.01670.450.01670.220.01670.900.01670.710.01671.410.01672.120.01670.950.01670.630.01670.320.0167])= \text{round}\left(\left[\begin{array}{ccc} \frac{0.18}{0.0167} & \frac{0.37}{0.0167} & \frac{0.55}{0.0167} \\ \frac{0.45}{0.0167} & \frac{0.22}{0.0167} & \frac{0.90}{0.0167} \\ \frac{0.71}{0.0167} & \frac{1.41}{0.0167} & \frac{2.12}{0.0167} \\ \frac{0.95}{0.0167} & \frac{0.63}{0.0167} & \frac{0.32}{0.0167} \end{array}\right]\right)=round 0.01670.180.01670.450.01670.710.01670.950.01670.370.01670.220.01671.410.01670.630.01670.550.01670.900.01672.120.01670.32

=round([10.7822.1632.9326.9513.1753.8942.5184.43126.9556.8937.7219.16])= \text{round}\left(\left[\begin{array}{ccc} 10.78 & 22.16 & 32.93 \\ 26.95 & 13.17 & 53.89 \\ 42.51 & 84.43 & 126.95 \\ 56.89 & 37.72 & 19.16 \end{array}\right]\right)=round 10.7826.9542.5156.8922.1613.1784.4337.7232.9353.89126.9519.16

≈[1122332713544384127573819]\approx \left[\begin{array}{ccc} 11 & 22 & 33 \\ 27 & 13 & 54 \\ 43 & 84 & 127 \\ 57 & 38 & 19 \end{array}\right]≈ 1127435722138438335412719

反量化验证：

X~=Xˉ⋅ΔX^\tilde{X} = \bar{X} \cdot \Delta_{\hat{X}}X~=Xˉ⋅ΔX^

=[33538457162712738]⋅0.0167= \left[\begin{array}{cccc} 33 & 53 & 84 & 57 \\ 16 & 27 & 127 & 38 \end{array}\right] \cdot 0.0167=[33165327841275738]⋅0.0167

≈[0.550.881.400.950.270.452.120.63]\approx \left[\begin{array}{cccc} 0.55 & 0.88 & 1.40 & 0.95 \\ 0.27 & 0.45 & 2.12 & 0.63 \end{array}\right]≈[0.550.270.880.451.402.120.950.63]

W~=Wˉ⋅ΔW^\tilde{W} = \bar{W} \cdot \Delta_{\hat{W}}W~=Wˉ⋅ΔW^

=[1122332713544384127573819]⋅0.0167= \left[\begin{array}{ccc} 11 & 22 & 33 \\ 27 & 13 & 54 \\ 43 & 84 & 127 \\ 57 & 38 & 19 \end{array}\right] \cdot 0.0167= 1127435722138438335412719 ⋅0.0167

≈[0.180.370.550.450.220.900.721.402.120.950.630.32]\approx \left[\begin{array}{ccc} 0.18 & 0.37 & 0.55 \\ 0.45 & 0.22 & 0.90 \\ 0.72 & 1.40 & 2.12 \\ 0.95 & 0.63 & 0.32 \end{array}\right]≈ 0.180.450.720.950.370.221.400.630.550.902.120.32

计算量化后的输出：

Y~=X~⋅W~\tilde{Y} = \tilde{X} \cdot \tilde{W}Y~=X~⋅W~

≈[0.550.881.400.950.270.452.120.63]⋅[0.180.370.550.450.220.900.721.402.120.950.630.32]\approx \left[\begin{array}{cccc} 0.55 & 0.88 & 1.40 & 0.95 \\ 0.27 & 0.45 & 2.12 & 0.63 \end{array}\right] \cdot \left[\begin{array}{ccc} 0.18 & 0.37 & 0.55 \\ 0.45 & 0.22 & 0.90 \\ 0.72 & 1.40 & 2.12 \\ 0.95 & 0.63 & 0.32 \end{array}\right]≈[0.550.270.880.451.402.120.950.63]⋅ 0.180.450.720.950.370.221.400.630.550.902.120.32

≈[1.992.994.382.243.995.62]\approx \left[\begin{array}{ccc} 1.99 & 2.99 & 4.38 \\ 2.24 & 3.99 & 5.62 \end{array}\right]≈[1.992.242.993.994.385.62]

误差分析：

原始输出 Y=[2.003.004.402.254.005.65]\text{原始输出 } Y = \left[\begin{array}{ccc} 2.00 & 3.00 & 4.40 \\ 2.25 & 4.00 & 5.65 \end{array}\right]原始输出 Y=[2.002.253.004.004.405.65]

量化输出 Y~≈[1.992.994.382.243.995.62]\text{量化输出 } \tilde{Y} \approx \left[\begin{array}{ccc} 1.99 & 2.99 & 4.38 \\ 2.24 & 3.99 & 5.62 \end{array}\right]量化输出 Y~≈[1.992.242.993.994.385.62]

绝对误差=Y−Y~≈[0.010.010.020.010.010.03]\text{绝对误差} = Y - \tilde{Y} \approx \left[\begin{array}{ccc} 0.01 & 0.01 & 0.02 \\ 0.01 & 0.01 & 0.03 \end{array}\right]绝对误差=Y−Y~≈[0.010.010.010.010.020.03]

平均绝对误差约为0.015，相对误差远小于1%，证明量化保持了较高的精度。

步骤6：硬件加速计算（INT8 GEMM）

在实际硬件实现中，使用INT8 GEMM内核直接计算量化后的矩阵乘法，然后进行缩放：
Y~=(Xˉ⋅Wˉ)⋅(ΔX^⋅ΔW^)\tilde{Y} = (\bar{X} \cdot \bar{W}) \cdot (\Delta_{\hat{X}} \cdot \Delta_{\hat{W}})Y~=(Xˉ⋅Wˉ)⋅(ΔX^⋅ΔW^)

其中 Xˉ⋅Wˉ\bar{X} \cdot \bar{W}Xˉ⋅Wˉ是使用硬件INT8 GEMM内核计算的，避免了反量化再量化的开销，显著提高了计算效率。