机器学习的三步走框架
Step 1: 定义函数集合
- 线性模型 :y=b+w⋅xy = b + w \cdot xy=b+w⋅x
- 参数:www (权重 weights), bbb (偏置 bias)。
- **局限性:线性模型太简单,无法拟合复杂的曲线(如折线、波浪线)。
- 深度学习模型 :
- 核心思想:任何连续曲线都可以用分段线性函数逼近。
- 激活函数 :引入非线性因素。
- Sigmoid :S形曲线,y=11+e−zy = \frac{1}{1 + e^{-z}}y=1+e−z1。早期常用,但计算量大且易梯度消失。
- ReLU :y=max(0,z)y = \max(0, z)y=max(0,z)。现代深度学习最常用,计算简单,由两个线性分段组成。
- 神经网络 :由大量神经元(Neuron,即带激活函数的线性单元)连接而成。
- Deep = Many hidden layers(许多隐藏层)。
Step 2: 定义损失函数
- 我们需要一个损失函数 L(b,w)L(b, w)L(b,w) 来衡量一组参数到底有多"烂"。
-
单点误差计算 :

- 假设 w=1,b=0.5kw=1, b=0.5kw=1,b=0.5k,我们把前一天的真实数据代入模型,得到预测值 y^\hat{y}y^。
- 然后通过公式 e=∣y−y^∣e = |y - \hat{y}|e=∣y−y^∣ 计算预测值与真实值(Label)之间的差距。
-
总体误差汇总 :

- 我们不能只看一天,要看过去几年(2017-2020)所有的数据。
- Loss的定义:所有训练数据误差的平均值。
- 公式通常有两种选择:
- **MAE **: L=1N∑∣y−y^∣L = \frac{1}{N} \sum |y - \hat{y}|L=N1∑∣y−y^∣ (取绝对值,对异常值不敏感)。
- **MSE : L=1N∑(y−y^)2L = \frac{1}{N} \sum (y - \hat{y})^2L=N1∑(y−y^)2 (平方误差,对大误差惩罚更重,这是线性回归最常用的)。
-
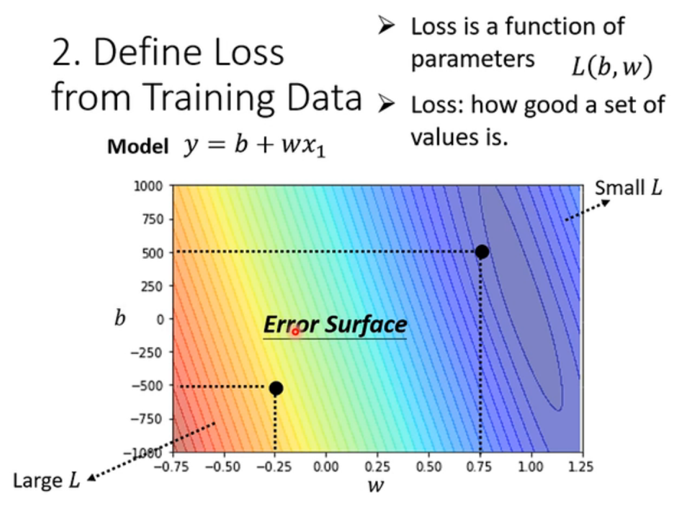
误差曲面:
- 这是一个非常重要的可视化概念。
- 横轴是 www,纵轴是 bbb,颜色代表 LossLossLoss 的大小。
- 深蓝色区域 代表 Loss 最小,红色区域代表 Loss 最大。
- 我们的目标 :就是在这个崎岖的地形中,找到位于"最深谷底"的那个点对应的 (w,b)(w, b)(w,b)。
-
Step 3: 优化
-
这一步是求解 。我们定义了目标是"最小化 Loss",即 w∗,b∗=argminw,bLw^*, b^* = \arg \min_{w,b} Lw∗,b∗=argminw,bL。怎么找呢?这里介绍最著名的算法:梯度下降。
-
直观理解 :
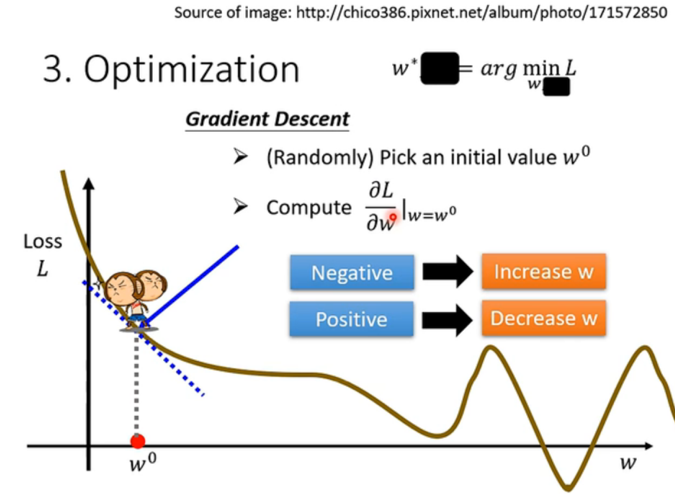
- 想象一只猴子站在山上(Loss Function的曲线上)。它想去谷底,但它看不见全貌,只能感觉到脚下的坡度(斜率/导数)。
- 如果斜率是负的 (左高右低),要想去低处,就得向右 走(增加 www)。
- 如果斜率是正的 (左低右高),要想去低处,就得向左 走(减小 www)。
-
数学原理与算法 :
-
随机初始化 :先随便选一个起始点 w0,b0w^0, b^0w0,b0。
-
计算梯度 :计算 Loss 对参数的偏导数 ∂L∂w\frac{\partial L}{\partial w}∂w∂L 和 ∂L∂b\frac{\partial L}{\partial b}∂b∂L。
-
参数更新公式(核心):
w1←w0−η∂L∂w w^1 \leftarrow w^0 - \eta \frac{\partial L}{\partial w} w1←w0−η∂w∂Lb1←b0−η∂L∂b b^1 \leftarrow b^0 - \eta \frac{\partial L}{\partial b} b1←b0−η∂b∂L
-
这里的 η\etaη ** 叫做学习率**。它是一个超参数,决定了你一步迈多大。
- η\etaη 太大:步子太大,可能跨过谷底(震荡甚至发散)。
- η\etaη 太小:步子太小,走到猴年马月也到不了谷底。
-
-
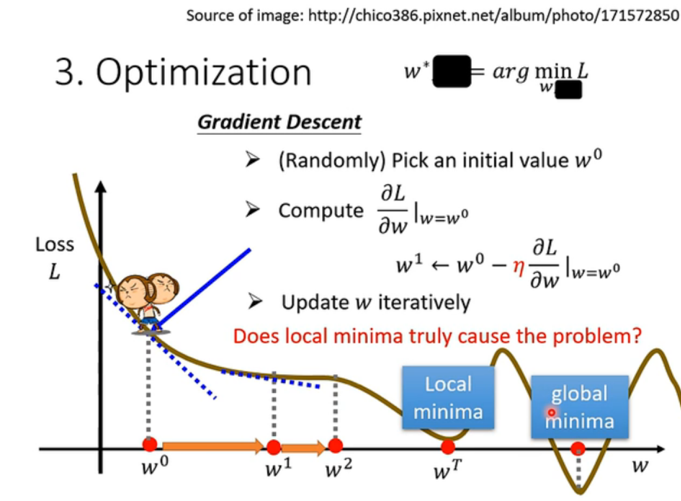
局部最小值与全局最小值 :
- 这也是深度学习中的一个经典问题。
- Global Minima(全局最优):整个地形的最低点。
- Local Minima(局部最优):一个小坑,虽然比周围低,但不是最低。
- 梯度下降的一个潜在问题是:如果猴子掉进了一个小坑(Local Minima),这里导数为0,它就会以为自己到终点了,从而不再移动,导致我们找不到真正的全局最优解。
-
2. 过拟合
- 现象:模型在训练集上表现极好(Loss很低),但在未见过的测试集(Unseen data)上表现变差。
- 原因:模型过于复杂(层数太深、参数太多),记住了训练数据的噪声而非规律。
- 图示:随着模型层数增加(1层 -> 2层 -> 3层...),训练误差降低,但测试误差先降后升。