[算法设计与分析-从入门到入土] 分治法

[算法设计与分析-从入门到入土] 分治法

个人导航

知乎：https://www.zhihu.com/people/byzh_rc

CSDN：https://blog.csdn.net/qq_54636039

注：本文仅对所述内容做了框架性引导，具体细节可查询其余相关资料or源码

参考文章：各方资料

文章目录

• [[算法设计与分析-从入门到入土] 分治法](#[算法设计与分析-从入门到入土] 分治法)
• 个人导航
• [分治法divide and conquer](#分治法divide and conquer)
• • • • 1.找到多数元素
      • [2.最小 / 最大值查找](#2.最小 / 最大值查找)
      • [3.第 k 小元素查找](#3.第 k 小元素查找)

分治法divide and conquer

分治范式:

• 分割（divide）：把原问题拆成 p p p 个规模更小的子问题 ( p ≥ 1 p≥1 p≥1)
• 解决（conquer）：如果子问题规模还不够小，就递归解决这些子问题
• 合并（combine）：把所有子问题的解合并起来，得到原问题的解

1.找到多数元素

多数元素: 出现次数 \> \\lfloor n/2 \\rfloor

1,3,2,3,3,4,3: 3是多数元素

1,3,2,3,3,4: 3不是多数元素

1. 初始化：设候选值 x = A [1]，计数器初始化为 1
2. 扫描数组：从 A [2] 开始逐个扫描元素：
   • 若当前元素等于 x，计数器加 1
   • 若当前元素不等于 x，计数器减 1
3. 终局判断：
   • 若全部扫描完成后计数器大于 0，返回 x 作为候选主元素
   • 若扫描至某元素 A [j]（1 < j < n）时计数器归零，则对子数组 A [j+1...n] 递归调用本算法

-> 验证其是否真的是多数元素

例子: 4, 4, 4, 1, 2, 3, 5

当前元素	与候选值 x 的关系	计数器	备注
4	等于 x (初始)	1
4	等于 x	2
4	等于 x	3
1	不等于 x	2
2	不等于 x	1
3	不等于 x	0	计数器归零，触发递归
5	-	递归处理子数组 [5]

-> 5 在原数组中仅出现 1 次，远小于 7/2 = 3.5，因此该数组没有多数元素

2.最小 / 最大值查找

将数组 A 划分为两个子数组: A [ 1... n 2 ] A[1...\frac{n}{2}] A[1...2n] 与 A [ n 2 + 1... n ] A[\frac{n}{2}+1...n] A[2n+1...n]

分别在两个子数组中查找最小值和最大值

最终返回两个最小值中的较小者and两个最大值中的较大者
C ( n ) = { 1 , n ≤ 2 2 C ( n 2 ) + 2 , n > 2 = 3 2 n − 2 \begin{align} C(n)&= \begin{cases} 1, \quad n \leq 2 \\ 2C(\frac{n}{2})+2, \quad n > 2 \end{cases} \\ &=\frac{3}{2}n-2 \end{align} C(n)={1,n≤22C(2n)+2,n>2=23n−2

3.第 k 小元素查找

从数组 A A A中选一个元素 m m mm mm, 将 A A A分为三个部分:
A 1 = { a ∣ a ∈ A ∩ a < m m } A 2 = { a ∣ a ∈ A ∩ a = m m } A 3 = { a ∣ a ∈ A ∩ a > m m } A_1=\{a|a\in A \cap a < mm\} \\ A_2=\{a|a\in A \cap a = mm\} \\ A_3=\{a|a\in A \cap a > mm\} A1={a∣a∈A∩a<mm}A2={a∣a∈A∩a=mm}A3={a∣a∈A∩a>mm}

三种情况判断第 k 小元素的位置:
A 1 : k ≤ ∣ A 1 ∣ A 2 : ∣ A 1 ∣ < k ≤ ∣ A 1 ∣ + ∣ A 2 ∣ A 3 : k > ∣ A 1 ∣ + ∣ A 2 ∣ \begin{align} A1&:\quad k\leq |A_1| \\ A2&:\quad |A_1|<k \leq |A_1|+|A_2| \\ A3&:\quad k > |A_1|+|A_2| \end{align} A1A2A3:k≤∣A1∣:∣A1∣<k≤∣A1∣+∣A2∣:k>∣A1∣+∣A2∣

关于mm的选择对效率的影响:

• 最坏情况：每次选到最大/最小元素，时间复杂度 Θ ( n 2 ) \Theta(n^2) Θ(n2)
• 最好情况：每次选到中位数，时间复杂度 O ( n ) O(n) O(n)

具体步骤: (共n个数)

• 先分m组(行), 每组 q = n m q=\frac{n}{m} q=mn个数
• 各组取中位数, 在m个中位数中找到中位数的中位数
• 统计小于, 等于, 大于该数的个数, 判断第k小元素在哪个集合中
• 在该新的集合中继续上述步骤
• 终止条件: 当集合数量小于阈值的时候, 直接排序

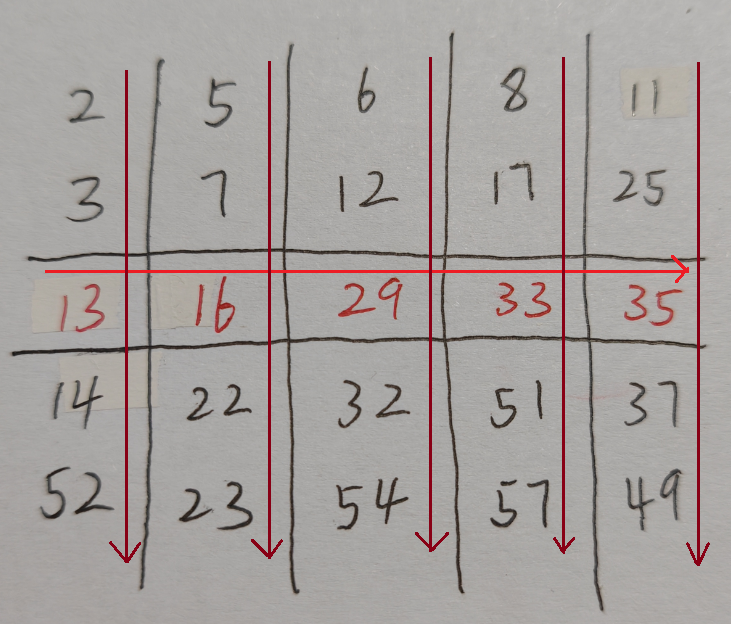
例子:

共 n = 25 n=25 n=25个数, 找第 k = ⌈ n / 2 ⌉ = 13 k=\lceil n/2 \rceil=13 k=⌈n/2⌉=13小的数, 也就是中位数

(将直接排序的阈值改为6个)

第 k 小元素查找 -> 讨论时间复杂度:

先横着依次放中间行, 再纵着依次放对应列:

先: 将中位数从小到大 放在中间行

再: 把各中间数的对应组顺序地从上到下排列

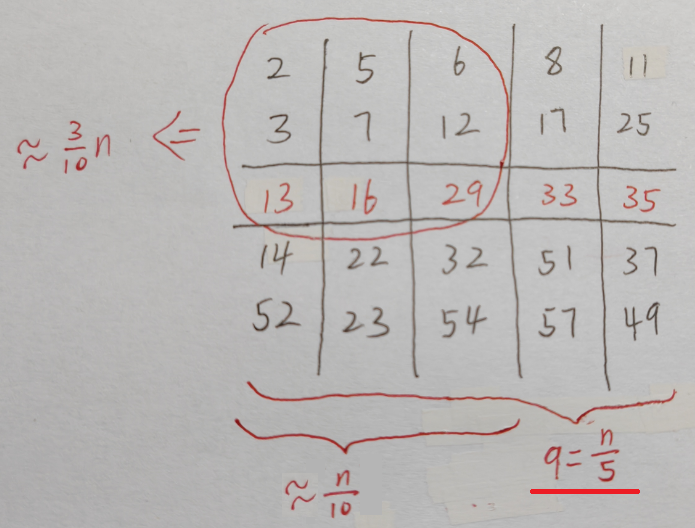
当分5组的时候( q = n / 5 q=n/5 q=n/5), A 1 A_1 A1或 A 3 A_3 A3最少约为 3 10 n \frac{3}{10}n 103n -> 最多约为 7 10 n \frac{7}{10}n 107n:

若:
f ( n ) = { 0 , n = 0 b , n = 1 f ( ⌊ c 1 n ⌋ ) + f ( ⌊ c 2 n ⌋ ) + b n , n ≥ 2 f(n)= \begin{cases} 0, \quad n = 0 \\ b, \quad n = 1 \\ f(\lfloor c_1n \rfloor)+f(\lfloor c_2n \rfloor)+bn, \quad n \geq 2 \end{cases} f(n)=⎩ ⎨ ⎧0,n=0b,n=1f(⌊c1n⌋)+f(⌊c2n⌋)+bn,n≥2

则:
f ( n ) = { O ( n l o g n ) , c 1 + c 2 = 1 O ( n ) , c 1 + c 2 < 1 f(n)= \begin{cases} O(nlogn), \quad c_1+c_2 = 1 \\ O(n), \quad c_1+c_2 < 1 \end{cases} f(n)={O(nlogn),c1+c2=1O(n),c1+c2<1

-> 当分五组时, q=n/5, T ( n ) ≤ T ( n 5 ) + T ( 7 10 n ) + Θ ( n ) T(n) \leq T(\frac{n}{5})+T(\frac{7}{10}n)+\Theta(n) T(n)≤T(5n)+T(107n)+Θ(n)

-> 则 c 1 + c 2 < 1 c_1+c_2 < 1 c1+c2<1, 为 O ( n ) O(n) O(n)

若 q = n / 3 q=n/3 q=n/3也就是分三组:

T ( n ) ≤ T ( n 3 ) + T ( 2 3 n ) + Θ ( n ) T(n) \leq T(\frac{n}{3})+T(\frac{2}{3}n)+\Theta(n) T(n)≤T(3n)+T(32n)+Θ(n)

-> O ( n l o g n ) O(nlogn) O(nlogn)
若 q = n / 7 q=n/7 q=n/7也就是分七组:

T ( n ) ≤ T ( n 7 ) + T ( 5 7 n ) + Θ ( n ) T(n) \leq T(\frac{n}{7})+T(\frac{5}{7}n)+\Theta(n) T(n)≤T(7n)+T(75n)+Θ(n)

-> O ( n ) O(n) O(n)