在内容安全领域,敏感词过滤是不可或缺的基础能力,广泛应用于社交平台、电商评论、即时通讯等场景。面对海量文本和庞大的敏感词库,如何实现高效的匹配过滤?Trie树(字典树/前缀树)凭借其对字符串前缀的高效利用,成为敏感词过滤的经典解决方案。本文将从Trie树的基本特性出发,深入拆解其用于敏感词过滤的核心原理,结合实例说明关键流程,助力开发者快速掌握这一技术的核心逻辑。
一、先搞懂:什么是Trie树?
Trie树是一种专门为处理字符串集合设计的树形数据结构,其核心思想是利用字符串的公共前缀减少重复存储和匹配开销。不同于二叉树、红黑树等通用树形结构,Trie树的每个节点都对应一个字符(或字符的占位符),从根节点到某一叶子节点的路径,恰好构成一个完整的字符串。
Trie树的节点通常包含两个核心属性:
-
子节点指针集合:用于指向当前字符的下一个可能字符(例如用哈希表、数组存储,key为字符,value为子节点);
-
结束标记(isEnd/endWord):标记当前节点是否为某一字符串的结尾(即从根到该节点的路径构成一个完整的敏感词)。
举个直观的例子:若敏感词库为["色情"、"色情电影"、"暴力"],构建的Trie树结构如下(简化示意):
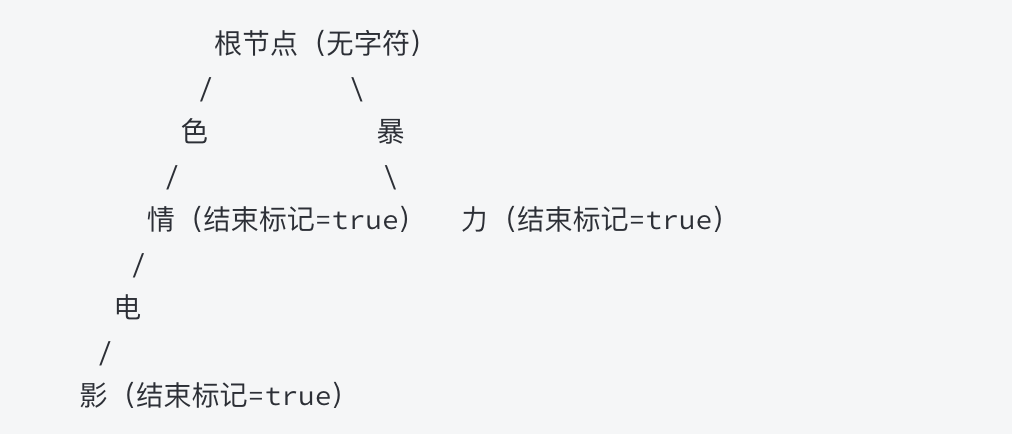
从结构能明显看出:"色情"和"色情电影"共享"色→情"的前缀路径,无需重复存储,这也是Trie树节省空间的关键。
二、Trie树实现敏感词过滤的核心逻辑
Trie树用于敏感词过滤的核心流程分为两步:离线构建Trie树 (将敏感词库写入树中)和在线查询匹配(遍历待检测文本,在树中查找敏感词)。下面结合实例详细拆解每一步的原理。
第一步:离线构建------将敏感词库植入Trie树
构建过程的核心是"逐词插入、共享前缀",本质是把每个敏感词的字符依次挂载到树中,同时在词的结尾节点标记结束状态。仍以敏感词库["色情"、"色情电影"、"暴力"]为例,步骤如下:
-
初始化根节点:创建一个空的根节点,作为整个树的入口;
-
插入"色情":从根节点开始,检查根节点的子节点中是否存在"色"字符。由于是首次插入,不存在则创建"色"节点,作为根节点的子节点;接着移动到"色"节点,检查其下是否存在"情"字符,同样创建"情"节点并挂载;最后移动到"情"节点,将其结束标记(isEnd)设为true,标识"色情"是完整敏感词;
-
插入"色情电影":同样从根节点出发,先匹配到已存在的"色"节点,再匹配到已存在的"情"节点;继续检查"情"节点的子节点,不存在"电"字符则创建"电"节点,再在"电"节点下创建"影"节点;最后将"影"节点的isEnd设为true,完成"色情电影"的插入;
-
插入"暴力":从根节点开始,检查到不存在"暴"字符,创建"暴"节点;移动到"暴"节点后,创建"力"节点并挂载,最后将"力"节点的isEnd设为true。
通过以上步骤,敏感词库就被完整植入Trie树中。核心优势在于,共享前缀的敏感词无需重复存储字符,极大节省了存储空间,同时为后续快速匹配奠定基础。
第二步:在线查询------遍历文本匹配敏感词
查询过程的核心是"逐字符遍历文本,沿Trie树路径匹配",即从文本的每个字符开始,尝试在Trie树中找到完整的敏感词路径。我们以待检测文本"这部色情电影很暴力"为例,拆解查询流程:
-
初始化指针:创建一个指针p,指向Trie树的根节点,用于追踪当前匹配的树节点;
-
遍历文本第一个字符"这":检查指针p(根节点)的子节点中是否存在"这"。不存在则说明以"这"开头的字符串不是敏感词,将指针p重置回根节点,继续下一个字符;
-
遍历"部"字符:重复上述逻辑,根节点下无"部"子节点,指针重置,继续下一个字符;
-
遍历"色"字符:根节点下存在"色"子节点,将指针p移动到"色"节点。此时检查"色"节点的isEnd是否为true(否),说明尚未匹配到完整敏感词,继续遍历下一个字符;
-
遍历"情"字符:"色"节点下存在"情"子节点,指针移动到"情"节点。检查isEnd为true,说明匹配到敏感词"色情",记录该敏感词;继续遍历下一个字符(不重置指针,因为可能存在更长的敏感词,如"色情电影");
-
遍历"电"字符:"情"节点下存在"电"子节点,指针移动到"电"节点,isEnd为false,继续遍历;
-
遍历"影"字符:"电"节点下存在"影"子节点,指针移动到"影"节点,isEnd为true,匹配到敏感词"色情电影",记录该词;
-
遍历"很"字符:"影"节点下无"很"子节点,将指针p重置回根节点,继续下一个字符;
-
遍历"暴"字符:根节点下存在"暴"子节点,指针移动到"暴"节点,isEnd为false;继续遍历"力"字符,"暴"节点下存在"力"子节点,指针移动后检查isEnd为true,匹配到敏感词"暴力",记录该词;
-
遍历结束:文本遍历完成,汇总所有记录的敏感词,完成过滤
这里需要注意一个关键逻辑:匹配到完整敏感词后不立即重置指针,而是继续遍历后续字符。这是为了捕获"包含式敏感词"(如"色情电影"包含"色情"),确保所有敏感词都能被检测到。若业务场景只需检测最长敏感词,可在匹配到完整词后根据需求决定是否继续。
三、Trie树敏感词过滤的核心优势
相比传统的暴力匹配、正则匹配等方式,Trie树在敏感词过滤场景下的优势尤为明显:
-
高效匹配性能:匹配效率仅与待检测文本的长度相关,与敏感词库的大小无关。假设文本长度为n,敏感词库大小为m,传统暴力匹配的时间复杂度为O(n*m),而Trie树的时间复杂度为O(n),在海量文本和大词库场景下优势显著;
-
节省存储空间:利用字符串的公共前缀共享存储节点,例如"色情"和"色情电影"共享"色→情"路径,无需重复存储这两个字符,词库越大,空间节省效果越明显;
-
支持多模式匹配:一次遍历文本即可匹配出所有存在的敏感词,无需对每个敏感词单独遍历文本,适合多敏感词同时检测的场景。
四、Trie树的局限性与优化方向
虽然Trie树优势突出,但在实际应用中仍存在局限性,需针对性优化:
1. 局限性
-
内存占用问题:若敏感词库包含大量无公共前缀的词(如"赌博""吸毒""诈骗"),Trie树会生成大量独立节点,导致内存占用激增;
-
字符集适配问题:对于中文等大字符集,若用数组存储子节点,会造成数组空间浪费;若用哈希表存储,会引入轻微的哈希计算开销;
-
长敏感词匹配效率下滑:对于极长的敏感词,需要沿树路径匹配多个字符,虽时间复杂度仍为O(n),但实际耗时会略增。
2. 优化方向
-
压缩Trie树:双数组Trie(DAT):将Trie树的节点和指针用两个数组(base数组和check数组)存储,大幅压缩内存占用,同时保持高效的查询性能,是工业级应用的常用优化方案;
-
结合AC自动机:Trie树单次匹配需回溯重置指针,AC自动机通过给每个节点添加失败指针,实现"一次遍历文本,匹配所有敏感词",解决了Trie树回溯的低效问题,更适合亿级流量的高并发场景;
-
文本预处理:在匹配前对文本进行归一化处理,如大小写转换、繁简转换、去除无意义字符(空格、表情、特殊符号),减少无效匹配,提升效率;
-
词库优化:合并冗余敏感词(如存在"色情电影"时,可根据业务需求决定是否保留"色情"),减少节点数量;对敏感词按长度排序,优先匹配长词,避免短词匹配后遗漏长词。
五、总结
Trie树通过"公共前缀共享存储"的核心思想,实现了敏感词过滤的高效匹配和空间优化,其核心流程可概括为"离线构建树(植入敏感词)+ 在线遍历匹配(检测文本)"。虽然存在内存占用、回溯低效等局限性,但通过双数组Trie、结合AC自动机等优化手段,可满足工业级场景的需求。
对于开发者而言,理解Trie树的过滤原理,不仅能掌握敏感词过滤的核心技术,更能深刻体会"数据结构适配业务场景"的设计思路------Trie树之所以能成为敏感词过滤的经典方案,正是因为它精准匹配了"多字符串前缀共享、高效多模式匹配"的核心需求。
后续若需应对高并发、海量流量场景,可基于本文原理进一步学习AC自动机与Trie树的结合实现,以及分布式环境下的敏感词过滤系统设计,让技术方案更贴合实际业务需求。