本篇来讲解二叉树的一些题目,来强化我们对二叉树的理解~
1. 另一棵树的子树
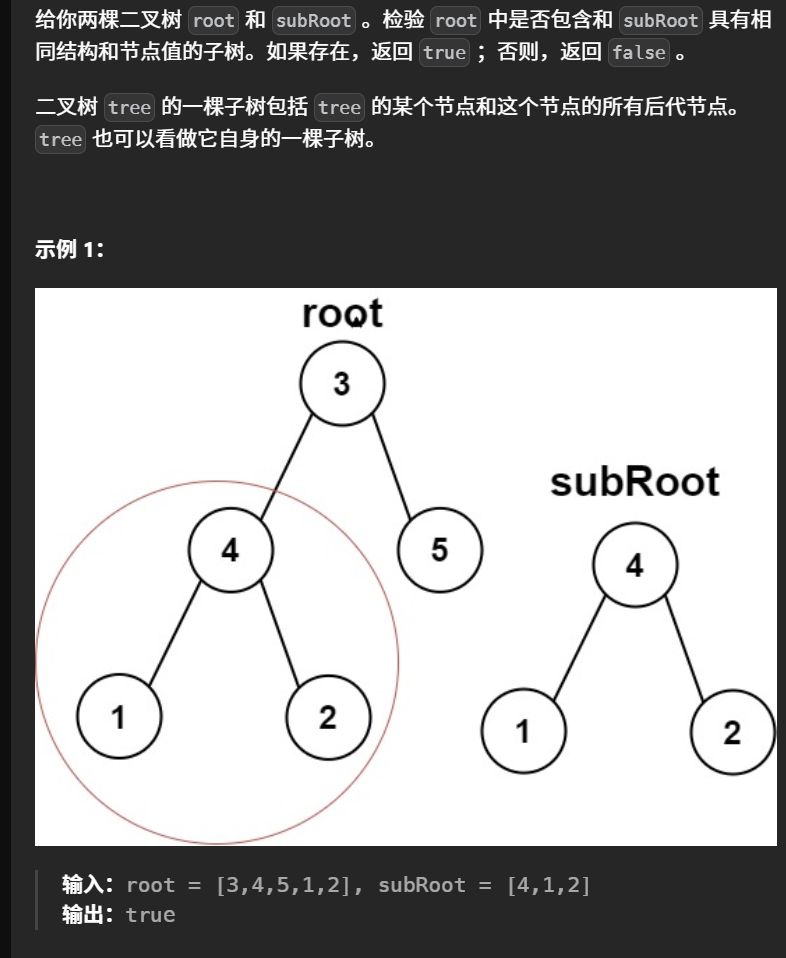
总结一下题目:我们有两棵二叉树,主二叉树为root,子二叉树为subRoot,我们要判断root中是否包含subRoot,要求为:结构相同且节点值相同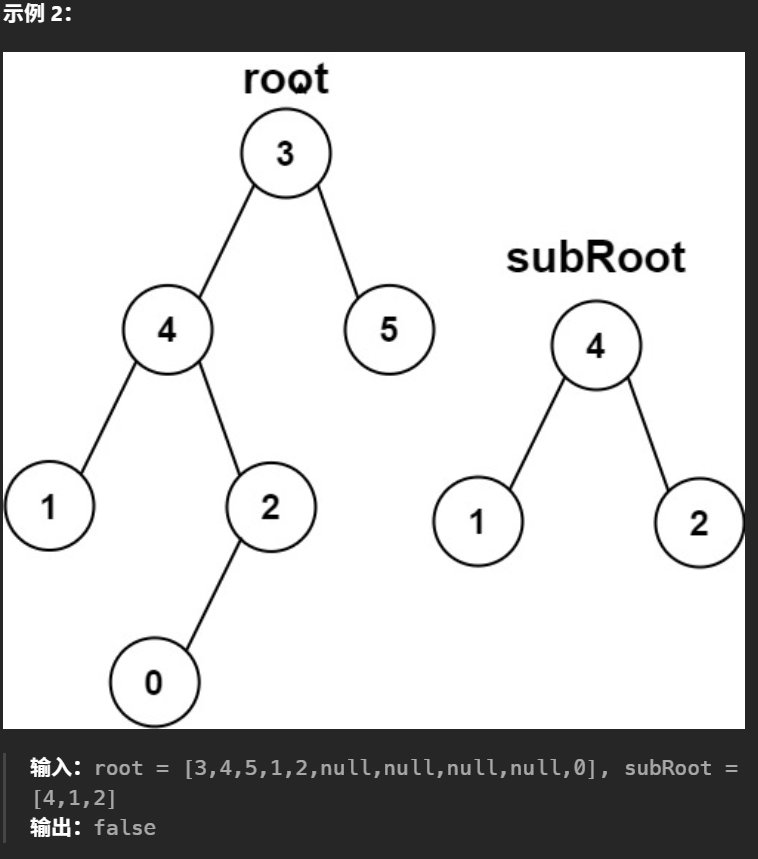
但是在实例2中,root在包含subRoot的情况下还有一个左树2,但是判为false,那么就可以理解为某个根节点下必须是和subRoot一模一样才能被认定为true(因为还需要算后代)。
总结完成,我们开始画图寻找思路~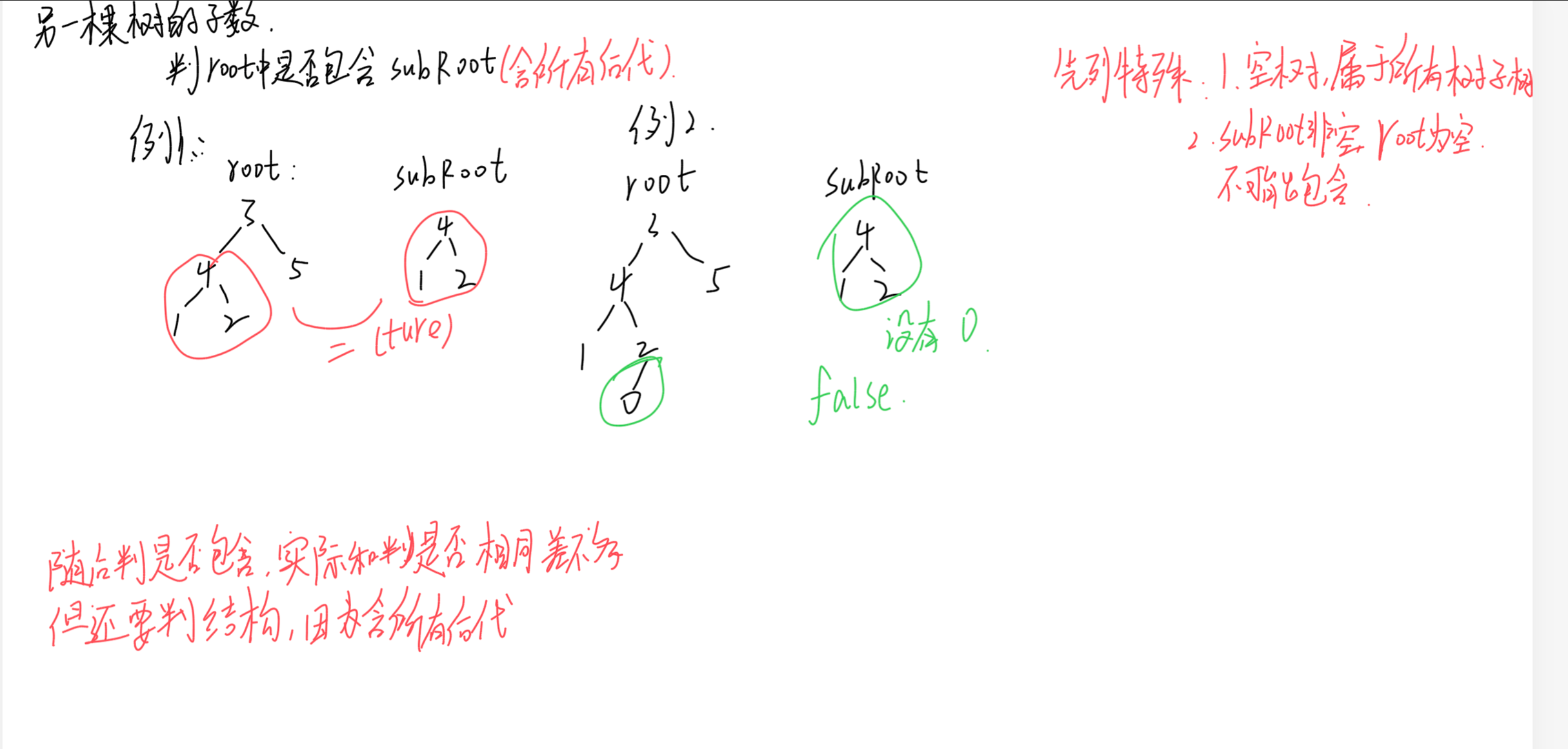
首先,如果root是一个空树且subRoot不为空树,那么root无法包含subRoot,是false。然后如果两个都是空树,可以认为是true。再是root不为空而subRoot为空,这个是true,因为空树是任何数的子树。
只要满足以下任一条件即可:
-
当前子树与 subRoot 相同
-
subRoot 是左子树的子树
-
subRoot 是右子树的子树
其实理下来之后感觉出了多了一些异常情况的处理之外,和判断两棵树是否相同很像,我觉得还要判subRoot是否是root的子树,要先判断结构在判断值是否相同。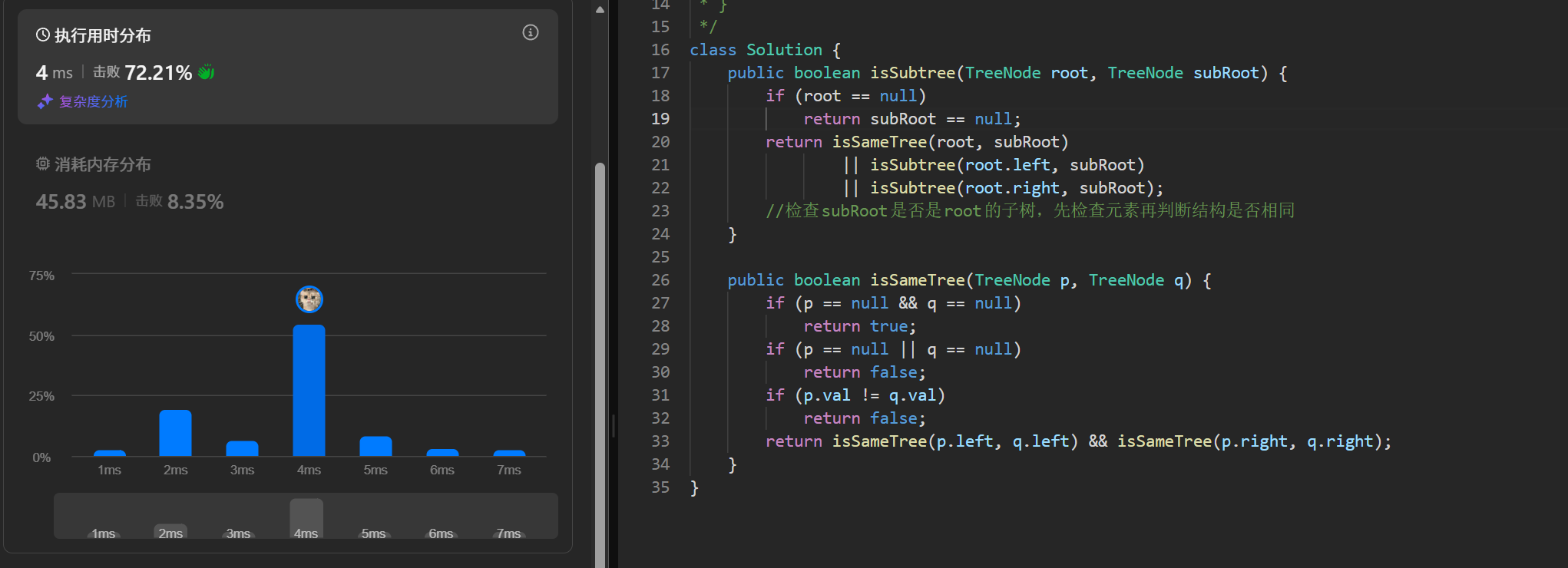
然后再去idea敲一遍完整的实例~ 题目实例是按照层序遍历的~所以我们还需要写一个层序遍历
java
package Tree;
import java.util.LinkedList;
import java.util.Queue;
public class Tree3 {
static class TreeNode{
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val){
this.val = val;
}
}
public static void levelOrder(TreeNode root){
if(root == null){
System.out.println("空树");
return;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()){
TreeNode cur = queue.poll();
System.out.print(cur.val+" ");
if (cur.left!=null){
queue.offer(cur.left);
}
if(cur.right!=null){
queue.offer(cur.right);
}
}
System.out.println();
}
public static boolean isSubtree(TreeNode root, TreeNode subRoot) {
//检查subRoot是否是root的子树,先检查元素再判断结构是否相同
if(root == null){
// 如果root为空,只有当subRoot也为空时才匹配
return subRoot == null;
}
return isSameTree(root,subRoot)//当前子树与 subRoot 相同
||isSubtree(root.left,subRoot)//subRoot 是左子树的子树
||isSubtree(root.right,subRoot);//subRoot 是右子树的子树
}
public static boolean isSameTree(TreeNode p, TreeNode q) {
if(p==null&&q==null){
return true;
}
if(p==null||q==null){
return false;
}
if(p.val!=q.val){
return false;
}
return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
}
public static void main(String[] args) {
System.out.println("====测试用例1====");
TreeNode root1 = new TreeNode(3);
root1.left = new TreeNode(4);
root1.right = new TreeNode(5);
root1.left.left = new TreeNode(1);
root1.left.right = new TreeNode(2);
TreeNode subRoot1 = new TreeNode(4);
subRoot1.left = new TreeNode(1);
subRoot1.right = new TreeNode(2);
System.out.println("root的层序遍历:");
levelOrder(root1);
System.out.println("subRoot的层序遍历:");
levelOrder(subRoot1);
boolean res1 = isSubtree(root1,subRoot1);
System.out.print("root是否包含subRoot:"+res1);
System.out.println("====测试用例2====");
TreeNode root2 = new TreeNode(3);
root2.left = new TreeNode(4);
root2.right = new TreeNode(5);
root2.left.left = new TreeNode(1);
root2.left.right = new TreeNode(2);
root2.left.right.left = new TreeNode(0);
TreeNode subRoot2 = new TreeNode(4);
subRoot2.left = new TreeNode(1);
subRoot2.right = new TreeNode(2);
System.out.println("root的层序遍历:");
levelOrder(root2);
System.out.println("subRoot的层序遍历:");
levelOrder(subRoot2);
boolean res2 = isSubtree(root2,subRoot2);
System.out.print("root是否包含subRoot:"+res2);
}
}以上就是本题的思路以及测试啦~主要思路是利用判断是否相同的基础上加上对树的更多条件判断
2. 平衡二叉树

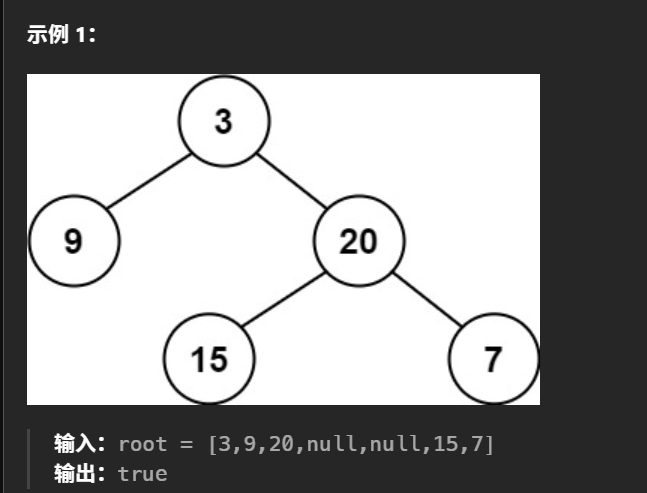
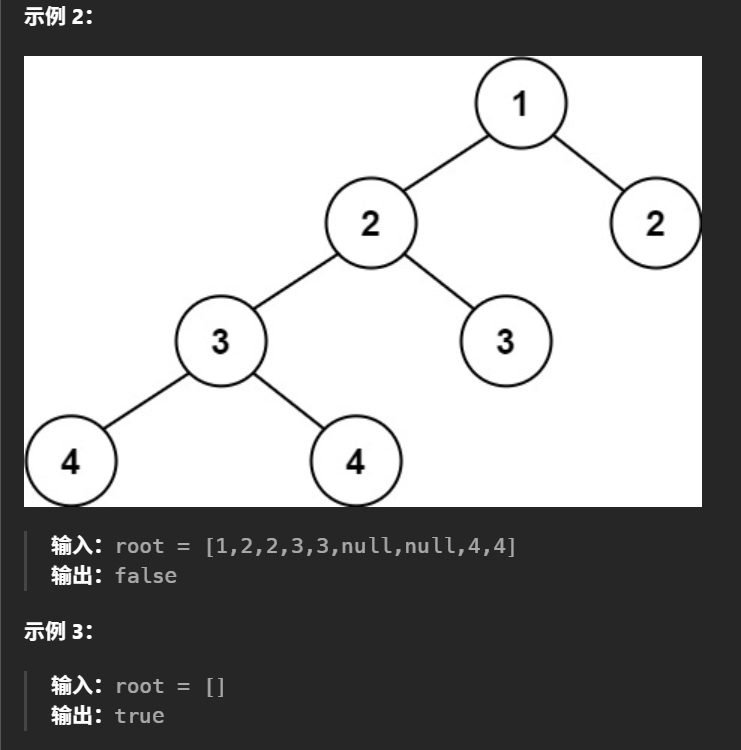
我们先看看平衡二叉树的概念是什么~
来画图找一找思路~
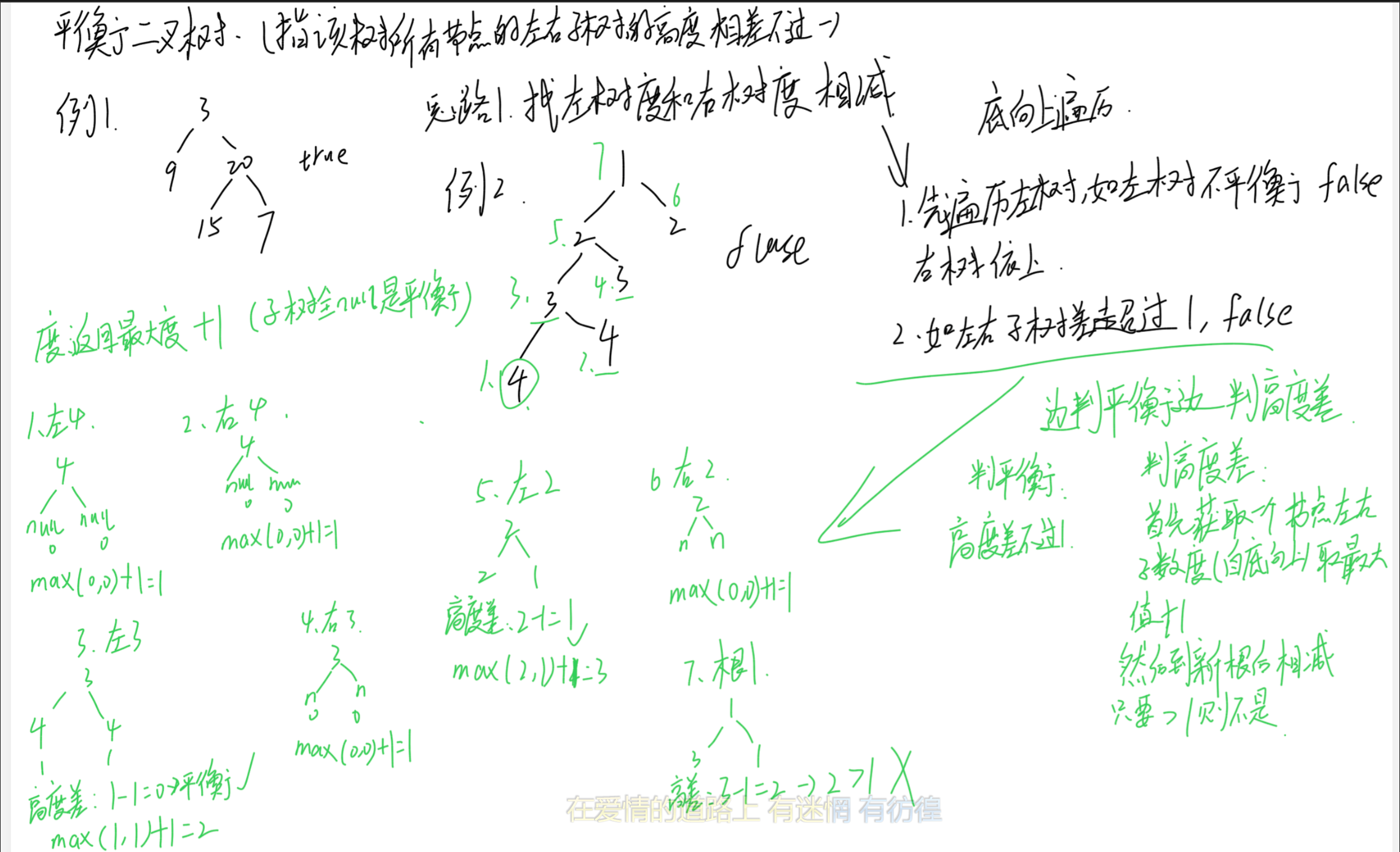
我们最终总结了几点:
- 我们需要找到根节点的左树度数和右树度数,然后将这两个度数相减,只要最终结果不超过1就可以判断为平衡二叉树
- 先从左树最后一个根节点的左子树开始判断度数差值,然后一直向上寻找(有右子树就找右子树的)直到到达根节点,开始寻找右树最后一个做孩子开始判断度数差,继续向上依此循环。
- 判断高度差的方法:我们先获取一个节点的左右子树的度(依据第二条里面的顺序),然后获取左右子树的高度差是否是1(如果一个节点的左子树或者右子树此前已经判断过则这个节点对应的子树继承上一次的度。)。度数取节点左右子树的最大值+1(比如上面笔记图里面的)。
- 子树全为null也可以算成是平衡二叉树。
- 我们假设,-1为不平衡否则是平衡的,在左子树不满足度数差不大于1(严格来说最好是等于1,因为计算度数是要左右子树的高度最大值+1的也就是说最差情况都有1),的情况下是平衡二叉树,如果是-1就不是平衡二叉树。
以下是代码实现~
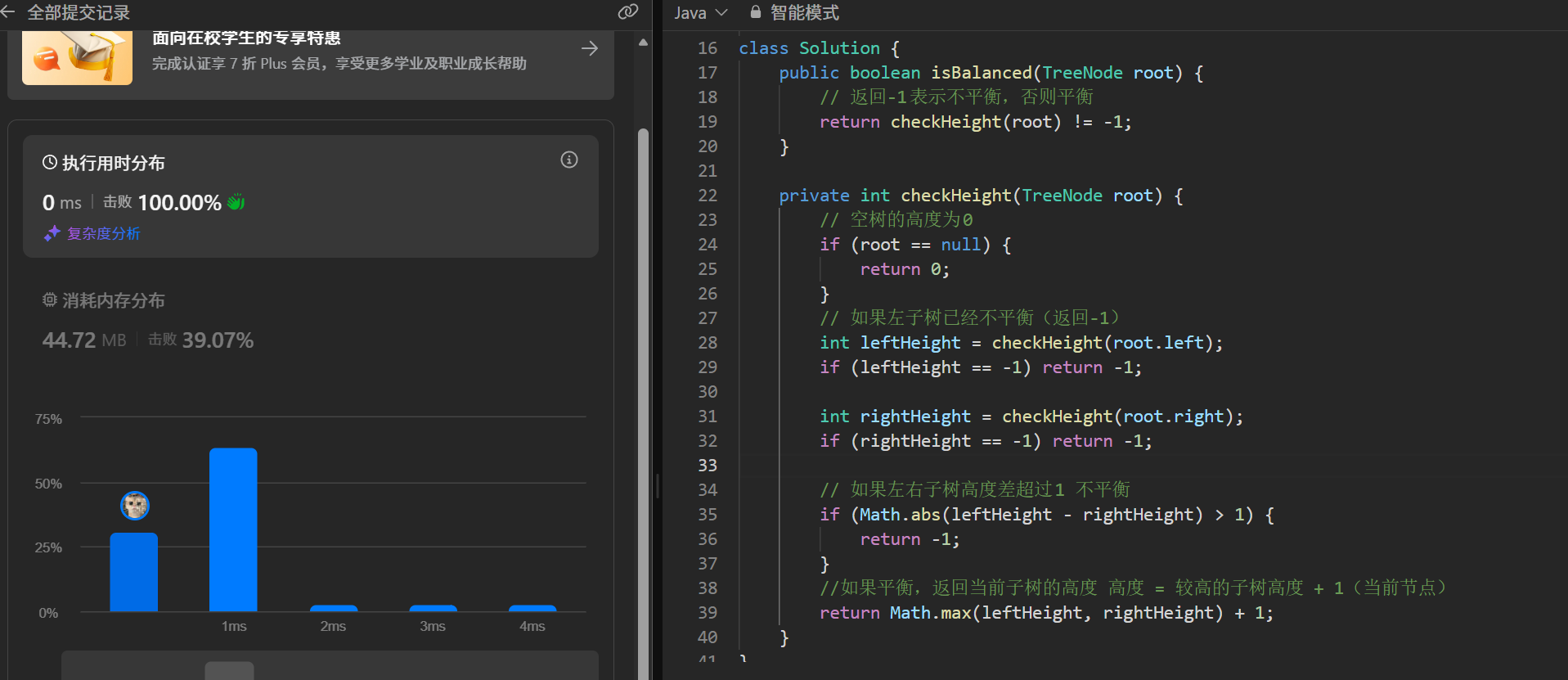
我们去idea敲一个测试用例~
java
package Tree;
import java.util.LinkedList;
import java.util.Queue;
public class Tree4 {
static class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public static void levelOrder(TreeNode root) {
if (root == null) return;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
System.out.print(cur.val + " ");
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
System.out.println();
}
public static boolean isBalanced(TreeNode root) {
// 返回-1表示不平衡,否则平衡
return checkHeight(root) != -1;
}
private static int checkHeight(TreeNode root) {
// 空树的高度为0
if (root == null) {
return 0;
}
// 如果左子树已经不平衡(返回-1)
int leftHeight = checkHeight(root.left);
if (leftHeight == -1) return -1;
int rightHeight = checkHeight(root.right);
if (rightHeight == -1) return -1;
// 如果左右子树高度差超过1 不平衡
if (Math.abs(leftHeight - rightHeight) > 1) {
return -1;
}
//如果平衡,返回当前子树的高度 高度 = 较高的子树高度 + 1(当前节点)
return Math.max(leftHeight, rightHeight) + 1;
}
public static void main(String[] args) {
System.out.println("====测试用例1====");
TreeNode root1 = new TreeNode(3);
root1.left = new TreeNode(9);
root1.right = new TreeNode(20);
root1.right.left = new TreeNode(15);
root1.right.right = new TreeNode(7);
System.out.println("root1的层序遍历为:");
levelOrder(root1);
boolean res1 = isBalanced(root1);
System.out.println("该树是否是平衡二叉树:"+res1);
System.out.println();
System.out.println("====测试用例2====");
TreeNode root2 = new TreeNode(1);
root2.left = new TreeNode(2);
root2.right = new TreeNode(2);
root2.left.left = new TreeNode(3);
root2.left.right = new TreeNode(3);
root2.left.left.left = new TreeNode(4);
root2.left.left.right = new TreeNode(4);
System.out.println("root2的层序遍历为:");
levelOrder(root2);
boolean res2 = isBalanced(root2);
System.out.println("该树是否是平衡二叉树:" + res2);
}
}3. 构建二叉树并遍历
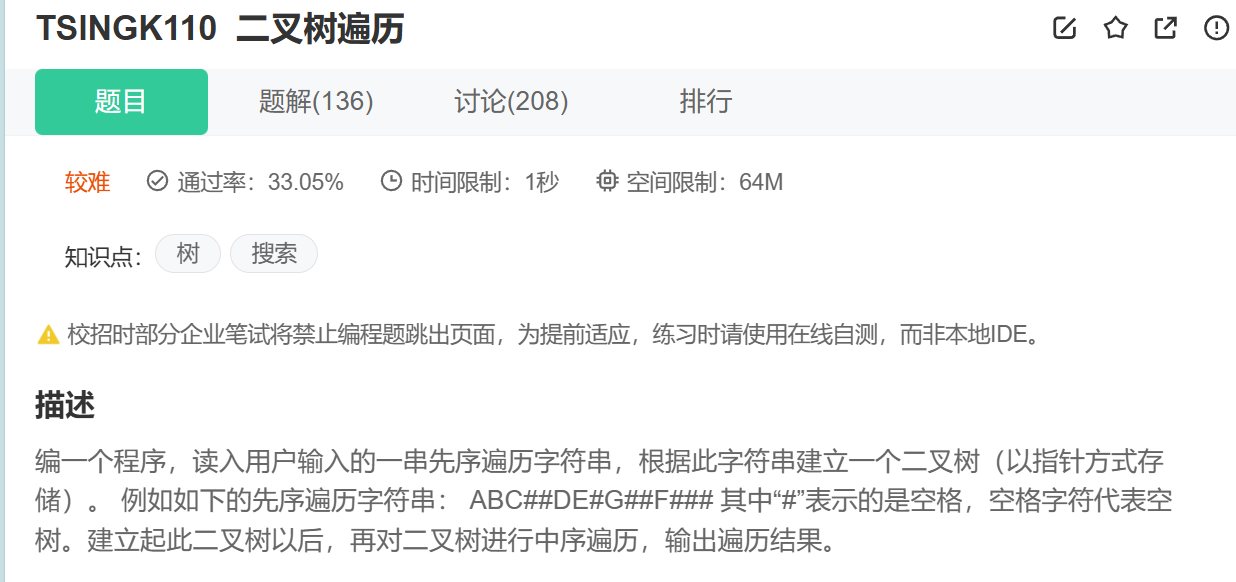
这个题的话呢,我觉得逻辑还是比较简单的,不太清楚为什么标为较难,可能是有一个很特别的做法吧,我把我的思路放出来:
其实就是获取元素建成二叉树,用前序的思路来做这道题,先建根再建左树和右树就可以了~
这里放一下牛客的代码:
java
import java.util.Scanner;
// 二叉树节点类
class TreeNode {
char val;
TreeNode left;
TreeNode right;
TreeNode(char val) {
this.val = val;
this.left = null;
this.right = null;
}
}
public class Main {
private static int index = 0; //遍历输入字符串
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String preorder = scanner.nextLine();
//构建二叉树
index = 0;
TreeNode root = buildTree(preorder);
// 进行中序遍历并输出结果
inorderTraversal(root);
}
/* 根据先序遍历字符串构建二叉树*/
private static TreeNode buildTree(String str) {
// 如果已经处理完所有字符或遇到空节点
if (index >= str.length() || str.charAt(index) == '#') {
index++;
return null;
}
// 创建当前节点
TreeNode node = new TreeNode(str.charAt(index));
index++;
node.left = buildTree(str);
node.right = buildTree(str);
return node;
}
/*中序遍历二叉树*/
private static void inorderTraversal(TreeNode root) {
if (root == null) {
return;
}
// 左 -> 根 -> 右
inorderTraversal(root.left);
System.out.print(root.val + " ");
inorderTraversal(root.right);
}
}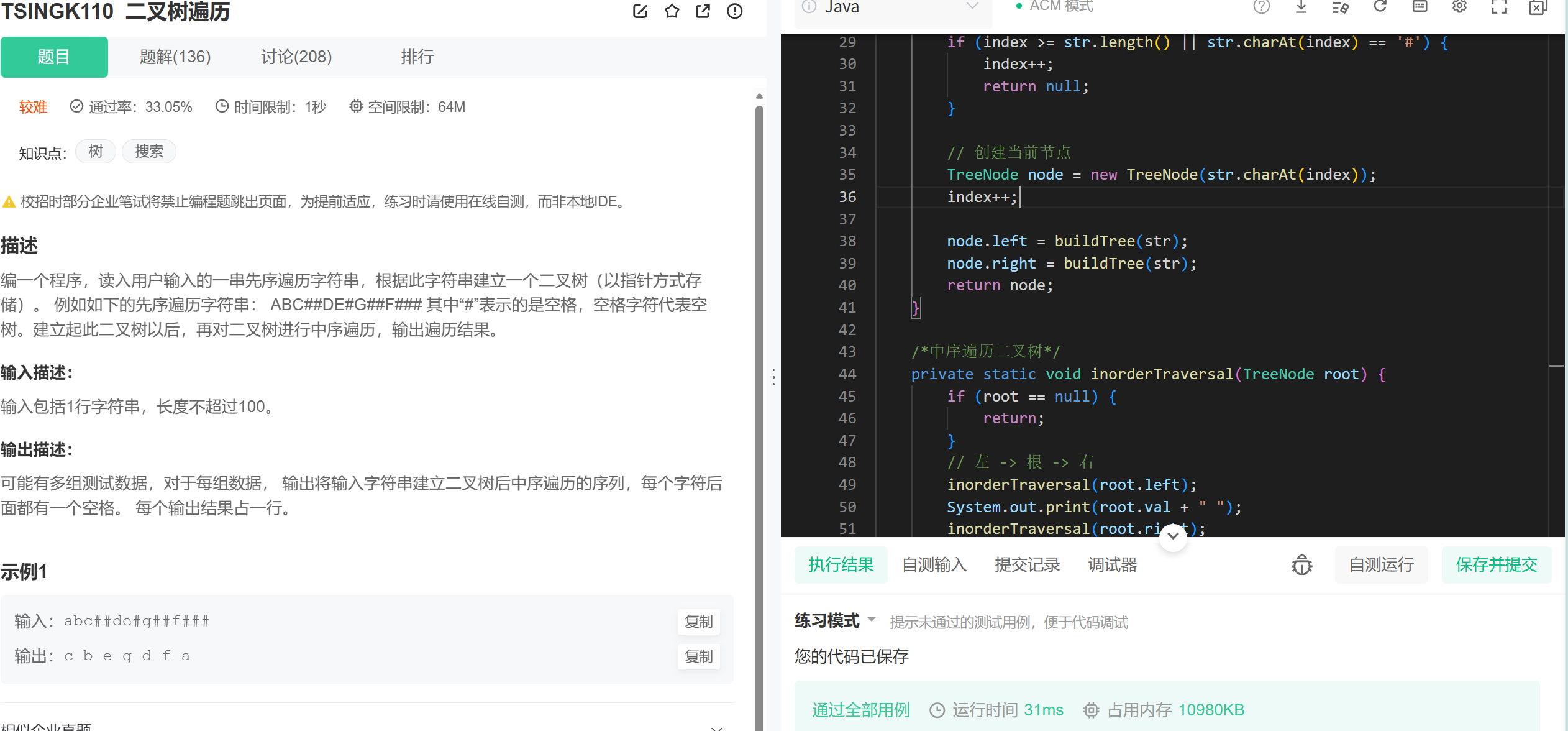
牛客的代码为了更直观看到解题过程我没有写测试实例,测试实例我在idea写:
java
package Tree;
import java.util.Scanner;
public class Tree5 {
static class TreeNode {
char val;
TreeNode left;
TreeNode right;
TreeNode(char val) {
this.val = val;
}
}
private static int index = 0; // 遍历输入字符串
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 测试1:固定测试用例
System.out.println("===== 测试用例1 =====");
String test1 = "ABC##DE#G##F###";
testBuildTree(test1);
// 测试2:另一个测试用例
System.out.println("\n===== 测试用例2 =====");
String test2 = "AB##C##";
testBuildTree(test2);
// 测试3:空树
System.out.println("\n===== 测试用例3 =====");
String test3 = "#";
testBuildTree(test3);
scanner.close();
}
private static void testBuildTree(String preorder) {
System.out.println("输入序列: " + preorder);
index = 0;
TreeNode root = buildTree(preorder);
System.out.print("中序遍历: ");
inorderTraversal(root);
System.out.println();
}
/* 根据前序遍历字符串构建二叉树 */
private static TreeNode buildTree(String str) {
if (index >= str.length() || str.charAt(index) == '#') {
index++;
return null;
}
TreeNode node = new TreeNode(str.charAt(index));
index++;
node.left = buildTree(str);
node.right = buildTree(str);
return node;
}
/* 中序遍历二叉树 */
private static void inorderTraversal(TreeNode root) {
if (root == null) {
return;
}
inorderTraversal(root.left);
System.out.print(root.val + " ");
inorderTraversal(root.right);
}
}4. 结合中序和后续构造二叉树
106. 从中序与后序遍历序列构造二叉树 - 力扣(LeetCode)
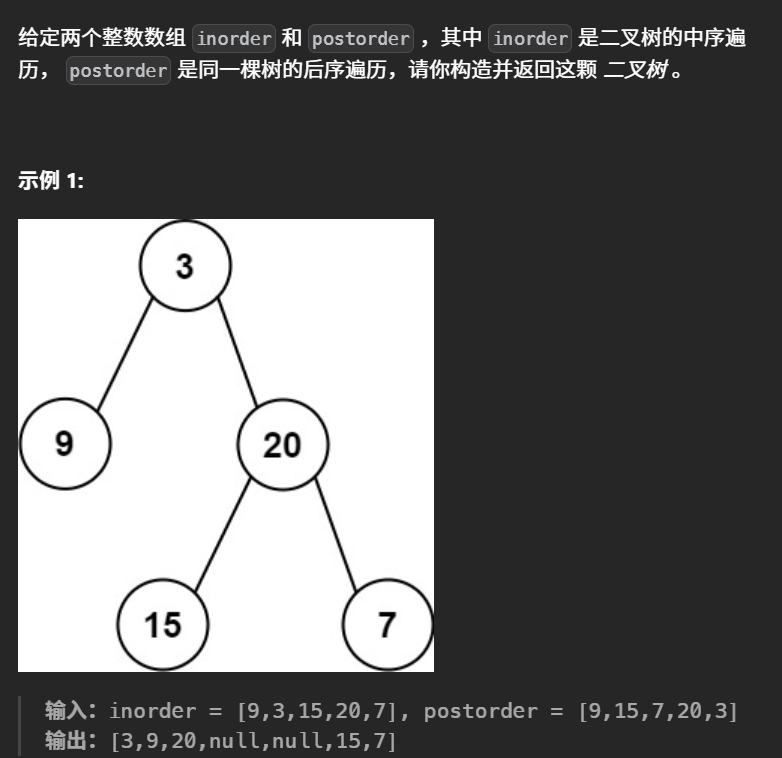
做这道题之前,我们先回顾一下中序遍历和后序遍历,中序遍历是左-根-右,后序遍历是左-右-根
中序只要有根节点就能推出左节点和右节点,后序有根节点也不知道前面是什么,所以这里选择
使用后序去辅助中序,因为后序最后一个是根,拿出后序的最后一个去在中序中间找左右去慢慢推

这就是构造的过程啦~还是比较简单的,根节点直接放,找左右依次放~ 不过上面是先放根节点,再放右节点,最后放左节点的!!
后序遍历:【左子树所有节点,右子树所有节点,根节点】
从后往前:根节点,右子树的最后一个节点.......,左子树的第一个节点,左子树的第一个节点......
所以先遇到的是根节点,然后是右子树的节点,最后是左子树的节点。
由于代码量比较大,不方便截力扣的图,这里直接放代码
java
int postIndex; //用于遍历postorder数组
public TreeNode buildTree(int[] inorder, int[] postorder) {
postIndex = postorder.length - 1; // 后序遍历的根节点在最后
return build(inorder, postorder, 0, inorder.length - 1);
}
private TreeNode build(int[] inorder, int[] postorder, int left, int right) {
if (left > right) {
return null;
}
// 1. 从后序遍历中取当前根节点(后序遍历的最后一个元素是根)
TreeNode root = new TreeNode(postorder[postIndex]);
// 2. 在中序遍历中找到根节点的位置
int index = findIndex(inorder, left, right, postorder[postIndex]);
if (index == -1) {
return null;
}
postIndex--; // 移动到下一个根节点
// 3. 递归构建左右子树
// 注意:必须先构建右子树,再构建左子树!
// 因为后序遍历的顺序是:左子树 -> 右子树 -> 根
// 当我们从后往前遍历postorder时,遇到的顺序是:根 -> 右子树 -> 左子树
root.right = build(inorder, postorder, index + 1, right); // 先构建右子树
root.left = build(inorder, postorder, left, index - 1); // 再构建左子树
return root;
}
private int findIndex(int[] inorder, int left, int right, int val) {
for (int i = left; i <= right; i++) {
if (inorder[i] == val) {
return i;
}
}
return -1;
}
也是可以通过的~注意事项也在代码中写了~
以上就是今天的题目分享啦~点点关注我们每天再见~