牛客小白月赛 D[差分] E [暴力枚举] F[] g[二阶差分]

直接暴力会tle 我们可以算出每个曲目的舒适区间可以合并就合并然后用差分维护每个值下舒适区间的数目总数减去舒适的数目就是不舒适的数目；

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
struct node {
    int l,r;
}a[N];
int d[N],ans[N];
int n,q;
void solve(){
    cin>>n>>q;
    memset(d,0,sizeof d);
    memset(ans,0,sizeof ans);
    for(int i=1;i<=n;i++){
        cin>>a[i].l>>a[i].r;
        int l1=a[i].l-1,r1=a[i].l+1;
        int l2=a[i].r-1,r2=a[i].r+1;
        if(r1>=l2&&r2>=l1){
            int l3=min(l1,l2);
            int r3=max(r1,r2);
            d[l3]++;d[r3+1]--;
        }else {d[l1]++;d[l2]++;d[r1+1]--;d[r2+1]--;}
    }
    for(int i=0;i<=n;i++){
        ans[i]=ans[i-1]+d[i];
    }
    while(q--){
        int x;cin>>x;   
        cout<<n-ans[x]<<' ';
    }cout<<'\n';
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t;cin>>t;
    while(t--)solve();    
    return 0;
}

暴力枚举枚举操作1的所有情况下操作2 的次数然后计算代价取最小值

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
#define int long long
int x,a,b,c;
int getadd(int x,int c){
    int l=1005,r=1010;
    //扩大位数
    for(int i=0;i<=15;i++){
        if(x>=l&&x<=r)return 0;
        if(x<l){
            int k=(l-x+c-1)/c;//为了到达l最少要加多少次c  向上取整
            if(x+k*c<=r)//补齐后在上界内;
                return k;
        }
        if(i<15){//更新l,r
            l*=10;
            r=r*10+9;
        }
    }
    return 1e18;
}
void solve(){
    cin>>x>>a>>b>>c;
    int ans=4e18,count=0;
    //枚举砍多少位
    while(1){
        int addk=getadd(x,c);
        int cost=count*a+addk*b;
        ans=min(ans,cost);
        if(x==0)break;
        x/=10;
        count++;
    }
    cout<<ans<<'\n';
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t;cin>>t;
    while(t--)solve();
    return 0;
}

F-小红开机厅_牛客小白月赛126

这道题有个结论当点位于两点所构成的矩形内那么他到两点的曼哈顿距离之和永远相等等于矩形的长+宽如果在矩形之外那么到两点的曼哈顿距离和（记作K）相等的点有2*K个

证明：

几何证明：

红色部分四个角落为孤立的点一个单位长度为一个点点的个数和这个直角三角形的边长相等

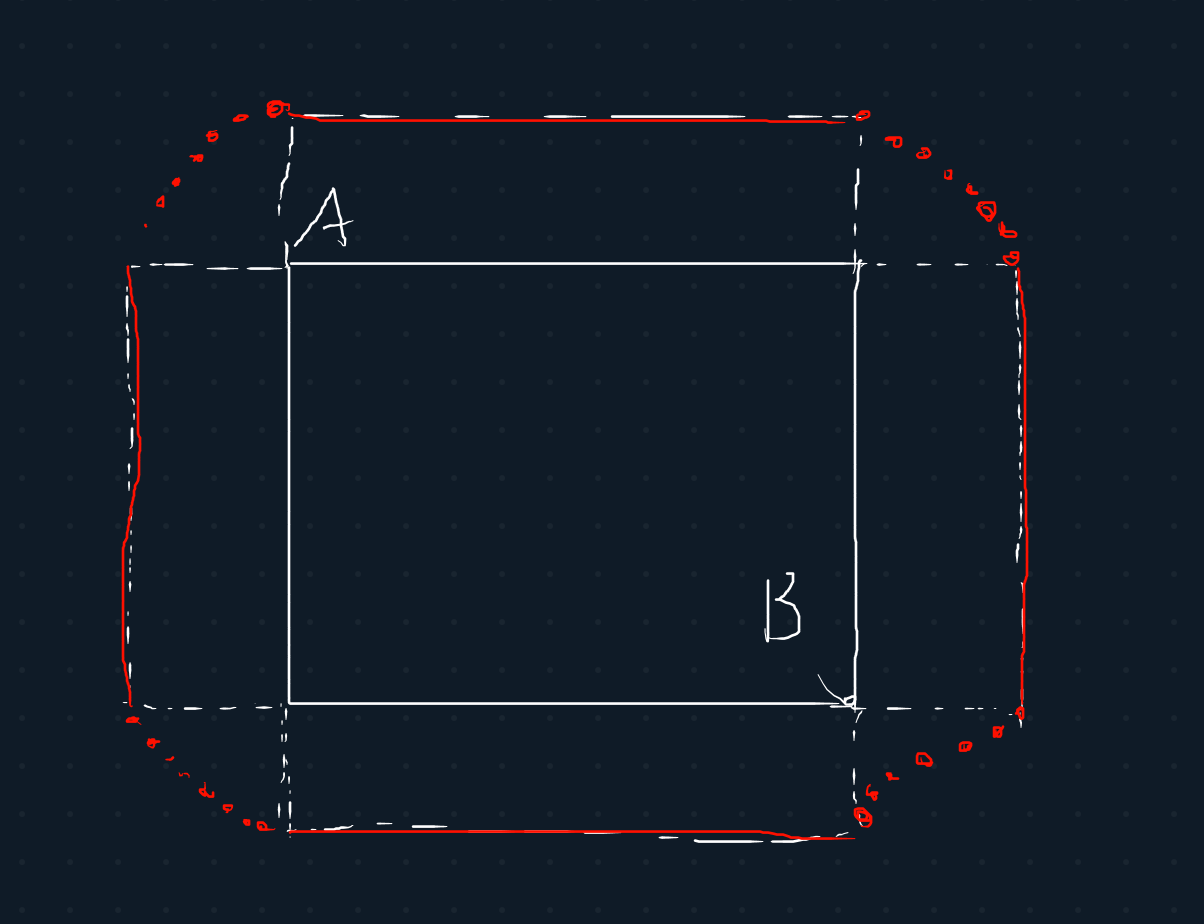
代码实现

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
long long n,xa,ya,xb,yb;
long long dis[N];
void solve(){
    memset(dis,0,sizeof dis);
    cin>>n;cin>>xa>>ya>>xb>>yb;
    int home=2;
    if(xa==xb&&ya==yb)home=1;
    unordered_map<long long,int>m;
    long long X=abs(xa-xb),Y=abs(ya-yb);
    long long L=X+Y;
    for(int i=1;i<=n;i++){
        long long xi,yi;
        cin>>xi>>yi;
        dis[i]=abs(xi-xa)+abs(yi-ya)+abs(xi-xb)+abs(yi-yb);
        m[dis[i]]++;
    }
    for(int i=1;i<=n;i++){
        long long ans=0;
        if(dis[i]==L)ans=(X+1)*(Y+1)-home;
        else ans=2*dis[i];
        ans-=m[dis[i]];
        cout<<ans<<' ';
    }
    cout<<'\n';
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t;cin>>t;
    while(t--)solve();    
    return 0;
}

G-小红越级（hard）_牛客小白月赛126

距离不同产生的不舒适感线性增长我们可以用差分的差分进行维护

cpp 复制代码

#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
#define int long long
int d[N],dd[N],a[N];
void solve(){
    memset(d,0,sizeof d);
    memset(dd,0,sizeof dd);
    memset(a,0,sizeof a);
    int n,q;cin>>n>>q;
    for(int i=1;i<=n;i++){
        int l,r;cin>>l>>r;
        if(l-1>1){
            d[1]+=(l-2);
            dd[2]--;dd[l]++;
        }
        dd[r+2]++;
        if(l<r-2){//中间
            int lp=(l+r)/2;
            int rp=lp+1;
            dd[l+2]++;dd[rp]--;
            d[rp]-=(lp-l-1);
            d[rp]+=(r-rp-1);
            dd[rp+1]--;
            dd[r]++;
        }
    }
    int sum=0;
    for(int i=1;i<=n;i++){
        sum+=dd[i];
        d[i]+=sum;
    }
    for(int i=1;i<=n;i++){
        a[i]=a[i-1]+d[i];
    }
    while(q--){
        int x;cin>>x;
        cout<<a[x]<<' ';
    }
    cout<<'\n';
}
signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t;cin>>t;
    while(t--)solve();
    return 0;
}