强化学习入门第二课:价值学习------从"试错"到"预判"的飞跃
本次讲解目标:理解什么是价值学习?为什么它比"盲目试错"更高效?如何用数学描述"一个状态值多少钱"?
一、概念回顾
上次在强化学习基础概念讲解中,我们搭建了强化学习的"世界观":
智能体(Agent) 在 环境(Environment) 中不断感知状态 s s s → 选择动作 a a a → 获得奖励 r r r → 进入新状态 s ′ s' s′,循环往复;
奖励是唯一的反馈信号,但我们要的不是"眼前小利",而是长期累积回报:
U t = R t + γ R t + 1 + γ 2 R t + 2 + ⋯ U_t = R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \cdots Ut=Rt+γRt+1+γ2Rt+2+⋯
由于策略随机性 ( π ( a ∣ s ) \pi(a|s) π(a∣s))和环境随机性 ( p ( s ′ ∣ s , a ) p(s'|s,a) p(s′∣s,a)),同一局面下,多次尝试会得到不同回报------就像买同一支股票,每次盈亏都可能不同。
为此,我们引入期望:用统计平均代替单次运气,定义了两个核心函数:
- 动作价值函数 Q π ( s , a ) Q^\pi(s, a) Qπ(s,a):在状态 s s s 下先做动作 a a a ,之后全按策略 π \pi π 走------预期能拿多少收益?
- 状态价值函数 V π ( s ) V^\pi(s) Vπ(s):在状态 s s s 下,完全交给策略 π \pi π 自动决策------预期能拿多少收益?
关键: Q Q Q 和 V V V 不是"发生了什么",而是"在不确定环境中,大概率会发生什么"------它们本质上是智能体对世界的价值抽象模型。
二、为什么有了"试错",还需要"价值"?
既然智能体可以通过不断试错(比如随机动作 + 看奖励)慢慢学会"什么动作好",那为何还要折腾 Q , V Q, V Q,V 这些抽象函数?
🤔 想象一个小孩学骑自行车:
- 试错模式:摔倒 100 次后,隐隐约约知道"往左歪时该往右打方向";
- 价值认知模式:第 3 次摔倒时,他就想:"刚才身体前倾 + 车把太正 → 必倒;下次身体后仰 + 微调车把 → 或许能稳住。"
后者不是靠"多摔",而是靠**提前预判每个动作的后果**------这就是价值学习的核心思想!
纯试错(如蒙特卡洛随机探索)的问题:
| 问题 | 举例 | 后果 |
|---|---|---|
| 效率极低 | CartPole 随机策略平均撑 20 步 | 学 1000 局才勉强及格 |
| 延迟反馈难归因 | 吃金币得 +1,但真正关键是通关游戏 | 无法知道"哪步动作真正重要" |
| 无法泛化 | 通关第 1 关后,面对第 2 关仍像新手 | 没有"经验总结",全是"个案记忆" |
价值学习的本质: 把"每次试错"的经验,提炼成一张「状态/动作价值表」(这就是Q-learning的思想)------以后看到类似局面,直接查表决策,不用重头试!
就像老司机进隧道前就会减速,不是因为上次在这儿撞过,而是他知道:"隧道 = 光线突变 + 视野受限 = 高风险"。
三、什么是价值学习?------让智能体拥有"预判未来"的能力
我们将 价值学习(Value-Based Learning) 定义为:
通过与环境交互收集经验,逐步估计 V π ( s ) V^\pi(s) Vπ(s) 或 Q π ( s , a ) Q^\pi(s, a) Qπ(s,a) 的真实值,并用这些估计指导后续决策,最终逼近 最优价值函数 V ∗ ( s ) V^*(s) V∗(s) 或 Q ∗ ( s , a ) Q^*(s, a) Q∗(s,a),从而导出最优策略 π ∗ \pi^* π∗。

图中给出的例子是通过神经网络来学习价值估计。将游戏的画面(当前状态)送如一个图神经网络提取关键特征,然后通过一全连接网络输出当前环境下执行每个动作可能获得的收益。这种通过神经网络的实现叫做 Deep Q Network (DQN)Deep Q Network (DQN)。
需要注意的是:价值学习 ≠ 直接学策略;它学的是"每个局面值多少钱",再从中"贪心"地选出最佳动作。
四、核心突破:贝尔曼方程(Bellman Equation)------价值的"递归定义"
价值函数听起来很抽象,但它有一个惊人的自洽结构:
"现在这个状态值多少钱?" = "立刻能拿到的奖励" + "下一步状态的预期价值(打折后)"
这就是贝尔曼方程 ------价值学习的第一性原理。
1️⃣ 状态价值函数的贝尔曼期望方程(针对固定策略 π \pi π)
V π ( s ) = E a ∼ π ( ⋅ ∣ s ) [ R + γ E s ′ ∼ p ( ⋅ ∣ s , a ) [ V π ( s ′ ) ] ] \boxed{ V^\pi(s) = \mathbb{E}{a \sim \pi(\cdot|s)} \left[ \; R + \gamma \, \mathbb{E}{s' \sim p(\cdot|s,a)} \left[ V^\pi(s') \right] \; \right] } Vπ(s)=Ea∼π(⋅∣s)[R+γEs′∼p(⋅∣s,a)[Vπ(s′)]]
拆解这个式子(像剥洋葱):
- 最外层:对当前动作 a a a 求期望(按策略 π \pi π 选动作的概率加权);
- 中间: R R R 是执行 a a a 后的即时奖励 ;
- 最内层:对下一状态 s ′ s' s′ 求期望(按环境转移 p ( s ′ ∣ s , a ) p(s'|s,a) p(s′∣s,a) 加权),再乘折扣 γ \gamma γ,加上 V π ( s ′ ) V^\pi(s') Vπ(s′) ------ 即"下一步的长期价值"。
一句话总结:V π ( s ) V^\pi(s) Vπ(s) = 今天干的事( a a a)带来的即刻回报 + 明天局面( s ′ s' s′)的预期价值(折现后),再对所有可能路径取平均。
例子:马里奥站在金币前(状态 s s s)

假设策略 π \pi π 是:70% 跳、20% 左、10% 右;环境规则如下:
| 动作 a a a | 奖励 r r r | 下一状态 s ′ s' s′ | V π ( s ′ ) V^\pi(s') Vπ(s′) 估计值 |
|---|---|---|---|
| 跳(70%) | +1(吃金币) | 平台上方(安全) | +3.0 |
| 左(20%) | 0 | 原地 | +1.5 |
| 右(10%) | -1000(撞敌人) | 游戏结束 | 0.0 |
设 γ = 0.9 \gamma = 0.9 γ=0.9,则:
V π ( s ) = 0.7 ⋅ [ 1 + 0.9 × 3.0 ] + 0.2 ⋅ [ 0 + 0.9 × 1.5 ] + 0.1 ⋅ [ − 1000 + 0.9 × 0 ] = 0.7 × 3.7 + 0.2 × 1.35 + 0.1 × ( − 1000 ) = 2.59 + 0.27 − 100 = − 97.14 \begin{aligned} V^\pi(s) &= 0.7 \cdot \left[ 1 + 0.9 \times 3.0 \right] \\ &\quad + 0.2 \cdot \left[ 0 + 0.9 \times 1.5 \right] \\ &\quad + 0.1 \cdot \left[ -1000 + 0.9 \times 0 \right] \\ &= 0.7 \times 3.7 + 0.2 \times 1.35 + 0.1 \times (-1000) \\ &= 2.59 + 0.27 - 100 \\ &= -97.14 \end{aligned} Vπ(s)=0.7⋅[1+0.9×3.0]+0.2⋅[0+0.9×1.5]+0.1⋅[−1000+0.9×0]=0.7×3.7+0.2×1.35+0.1×(−1000)=2.59+0.27−100=−97.14
尽管"跳"很诱人,但因策略中仍有 10% 概率右走送命,整个状态 s s s 的价值被大幅拉低 !
→ 这就解释了为什么智能体要改进策略:把右走概率降为 0,价值立马飙升!
2️⃣ 动作价值函数 Q π ( s , a ) Q^\pi(s,a) Qπ(s,a) 的贝尔曼方程
类似地,固定"当前动作 a a a",得:
Q π ( s , a ) = E s ′ ∼ p ( ⋅ ∣ s , a ) [ R + γ E a ′ ∼ π ( ⋅ ∣ s ′ ) [ Q π ( s ′ , a ′ ) ] ] \boxed{ Q^\pi(s, a) = \mathbb{E}{s' \sim p(\cdot|s,a)} \left[ \; R + \gamma \, \mathbb{E}{a' \sim \pi(\cdot|s')} \left[ Q^\pi(s', a') \right] \; \right] } Qπ(s,a)=Es′∼p(⋅∣s,a)[R+γEa′∼π(⋅∣s′)[Qπ(s′,a′)]]
更直观写法(展开期望):
Q π ( s , a ) = ∑ s ′ p ( s ′ ∣ s , a ) [ r ( s , a , s ′ ) + γ ∑ a ′ π ( a ′ ∣ s ′ ) Q π ( s ′ , a ′ ) ] Q^\pi(s, a) = \sum_{s'} p(s'|s,a) \Big[\, r(s,a,s') + \gamma \sum_{a'} \pi(a'|s') \, Q^\pi(s', a') \,\Big] Qπ(s,a)=s′∑p(s′∣s,a)[r(s,a,s′)+γa′∑π(a′∣s′)Qπ(s′,a′)]
注意:
- 先对环境随机性 ( s ′ s' s′)平均;
- 再对策略随机性 ( a ′ a' a′)平均(因为下一步仍按 π \pi π 走)。
3️⃣ 终极目标:最优价值函数 V ∗ , Q ∗ V^*, Q^* V∗,Q∗
我们不满足于"某个策略的好坏",而想找到最牛策略 π ∗ \pi^* π∗ 。
定义:
- 最优状态价值函数 :
V ∗ ( s ) = max π V π ( s ) V^*(s) = \max_{\pi} V^\pi(s) V∗(s)=πmaxVπ(s) - 最优动作价值函数 :
Q ∗ ( s , a ) = max π Q π ( s , a ) Q^*(s, a) = \max_{\pi} Q^\pi(s, a) Q∗(s,a)=πmaxQπ(s,a)
其满足贝尔曼最优方程:
V ∗ ( s ) = max a E s ′ ∼ p ( ⋅ ∣ s , a ) [ R + γ V ∗ ( s ′ ) ] \boxed{ V^*(s) = \max_{a} \; \mathbb{E}_{s' \sim p(\cdot|s,a)} \left[ \, R + \gamma \, V^*(s') \, \right] } V∗(s)=amaxEs′∼p(⋅∣s,a)[R+γV∗(s′)]
Q ∗ ( s , a ) = E s ′ ∼ p ( ⋅ ∣ s , a ) [ R + γ max a ′ Q ∗ ( s ′ , a ′ ) ] \boxed{ Q^*(s, a) = \mathbb{E}{s' \sim p(\cdot|s,a)} \left[ \, R + \gamma \, \max{a'} Q^*(s', a') \, \right] } Q∗(s,a)=Es′∼p(⋅∣s,a)[R+γa′maxQ∗(s′,a′)]
关键区别:
V π , Q π V^\pi, Q^\pi Vπ,Qπ 中用的是 E a ′ [ ⋅ ] \mathbb{E}_{a'}[\,\cdot\,] Ea′[⋅] (按 π \pi π 选 a ′ a' a′);
V ∗ , Q ∗ V^*, Q^* V∗,Q∗ 中用的是 max a ′ \max_{a'} maxa′ (选最好的 a ′ a' a′)------即贪心最优。
有了 Q ∗ Q^* Q∗,最优策略直接得到:
π ∗ ( a ∣ s ) = { 1 , if a = arg max a ′ Q ∗ ( s , a ′ ) 0 , otherwise \pi^*(a|s) = \begin{cases} 1, & \text{if } a = \arg\max_{a'} Q^*(s, a') \\ 0, & \text{otherwise} \end{cases} π∗(a∣s)={1,0,if a=argmaxa′Q∗(s,a′)otherwise
五、如何学习价值?
假设我们不知道环境模型 p ( s ′ ∣ s , a ) p(s'|s,a) p(s′∣s,a) 和 r ( s , a , s ′ ) r(s,a,s') r(s,a,s′)(Model-Free),只能通过交互收集 ( s , a , r , s ′ ) (s, a, r, s') (s,a,r,s′) 四元组。
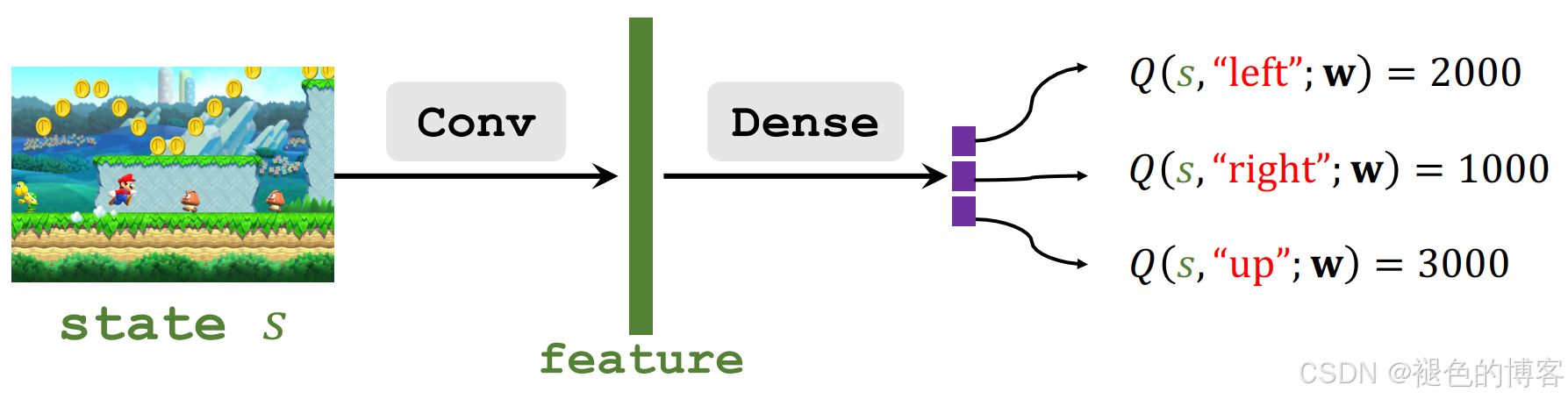
我们刚刚介绍了DQN,用神经网络来学习预测当前动作的价值。但是如何对模型的参数进行更新呢?
更新模型需要用模型预测的标签和真实的标签直接求Loss,才能使用梯度更新算法对模型参数进行更新,但现在的问题是这个真实标签我们不知道。
方法 1:蒙特卡洛(Monte Carlo, MC)------"整局复盘"
思想:打完一局游戏后,用实际回报 U t U_t Ut 去更新 V ( s t ) V(s_t) V(st) 或 Q ( s t , a t ) Q(s_t, a_t) Q(st,at)。
更新公式(每次访问型 MC):
V ( s ) ← V ( s ) + α [ U t − V ( s ) ] V(s) \gets V(s) + \alpha \big[ U_t - V(s) \big] V(s)←V(s)+α[Ut−V(s)]
其中 α ∈ ( 0 , 1 ) \alpha \in (0, 1) α∈(0,1) 是学习率, U t U_t Ut 是从时刻 t t t 开始的真实累积回报。
上面的公式都是对于 V ( s t ) V(s_t) V(st)的,对于 Q ( s t , a t ) Q(s_t, a_t) Q(st,at)也是一样的,这里就不做展开。
例子:马里奥第 5 步(状态 s 5 s_5 s5)选择"跳",之后得分为:+1, 0, +10, +0, -1000(死亡)
→ 若 γ = 0.9 \gamma = 0.9 γ=0.9,则:
U 5 = 1 + 0.9 ⋅ 0 + 0.9 2 ⋅ 10 + 0.9 3 ⋅ 0 + 0.9 4 ⋅ ( − 1000 ) ≈ − 656.1 U_5 = 1 + 0.9 \cdot 0 + 0.9^2 \cdot 10 + 0.9^3 \cdot 0 + 0.9^4 \cdot (-1000) \approx -656.1 U5=1+0.9⋅0+0.92⋅10+0.93⋅0+0.94⋅(−1000)≈−656.1
→ 用这个惨烈结果,大力下调 V ( s 5 ) V(s_5) V(s5) 的估计值。
优点:无偏估计(当采样无限多时, E [ U t ] = V π ( s ) \mathbb{E}[U_t] = V^\pi(s) E[Ut]=Vπ(s))
缺点:必须等到一局结束才能更新;高方差(运气影响大);无法处理无限任务(如自动驾驶永不停止)。
方法 2:时序差分(Temporal Difference, TD)------"边走边学"
思想:用"当前估计 + 下一步的估计" 去替代"等待整局结果"------更符合人类直觉!
最经典的 TD 更新 V ( s ) V(s) V(s):
V ( s ) ← V ( s ) + α [ r + γ V ( s ′ ) − V ( s ) ] \boxed{ V(s) \gets V(s) + \alpha \big[ \, r + \gamma V(s') - V(s) \, \big] } V(s)←V(s)+α[r+γV(s′)−V(s)]
其中:
- r + γ V ( s ′ ) r + \gamma V(s') r+γV(s′) 称为 TD Target(目标:这一步的合理预期)
- V ( s ) V(s) V(s) 是当前估计
- 差值 δ = r + γ V ( s ′ ) − V ( s ) \delta = r + \gamma V(s') - V(s) δ=r+γV(s′)−V(s) 叫 TD Error(误差:高估了?低估了?)
若用 Q Q Q 函数(也叫Q-learning),更新为 :
Q ( s , a ) ← Q ( s , a ) + α [ r + γ max a ′ Q ( s ′ , a ′ ) − Q ( s , a ) ] Q(s,a) \gets Q(s,a) + \alpha \big[\, r + \gamma \max_{a'} Q(s',a') - Q(s,a) \,\big] Q(s,a)←Q(s,a)+α[r+γa′maxQ(s′,a′)−Q(s,a)]
例子:出行时间预估。
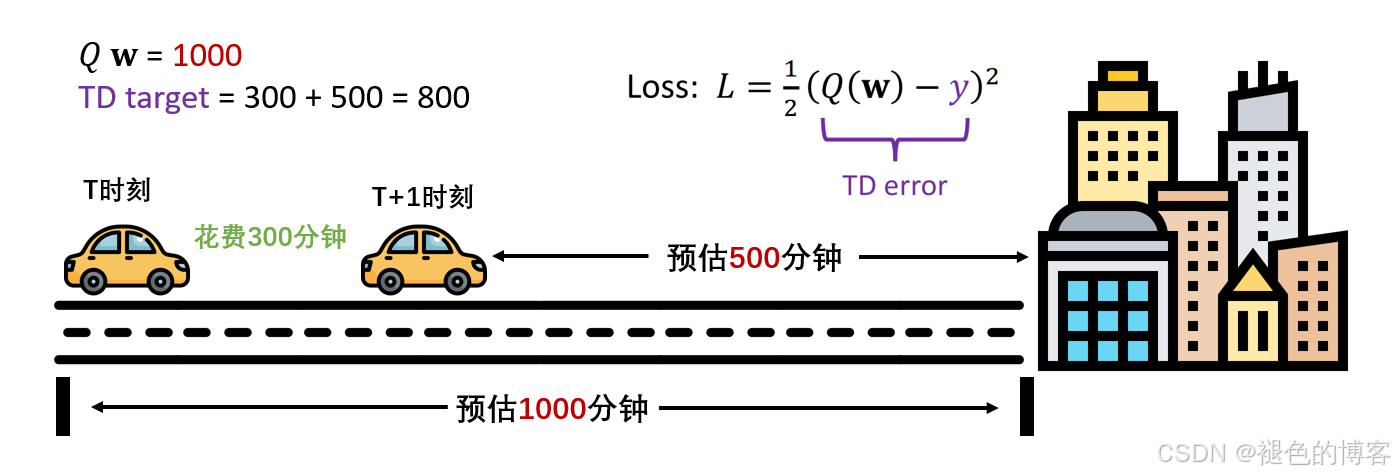
假设你现在出发去一个城市,但是你没去过,不知道需要花费多少时间。
模型先随机猜一个时间,1000分钟(实际可能850分钟)。
现在你出发到了中途的一个城市,花费了300分钟。此时模型对于当前位置,会预测一个从当前位置到目的地需要花费的时间,500分钟。
现在你有了3个时间,一个是模型一开始预测的全程时间1000,一个是你实际花费的部分时间300,还有一个是模型预测的剩余时间500。
用实际花费的时间加上预测的剩余时间,也能得到一个全称时间(300+500=800),那么和最初预测的时间1000相比,哪一个更准确?
显然是800。
TD算法的核心就是用 "当前估计 + 下一步的估计" 更新 "最初估计"
通过这个Loss,就能更新DQN中的参数了。
优点:单步更新、可在线学习、适用于无限任务
六、总结:价值学习------智能体的"经验提炼器"
| 视角 | 纯试错(随机探索) | 价值学习 |
|---|---|---|
| 决策依据 | 上次结果(单次) | 价值函数(期望) |
| 学习速度 | 慢(需海量尝试) | 快(一次经验可更新多个状态) |
| 泛化能力 | 弱(只记具体轨迹) | 强(用 V / Q V/Q V/Q 表达"局面好坏") |
| 理论基础 | 经验主义 | 贝尔曼方程 + 动态规划思想 |
智能不是记住所有答案,而是学会评估每个选择的长期后果。
就像围棋高手不靠死记棋谱,而是凭"棋形价值感"判断哪块更厚、哪里更薄。