**EM 算法(Expectation-Maximization Algorithm,期望最大化算法)** 是一种迭代算法,专门用于在包含**隐变量**或数据缺失的情况下,计算参数的**最大似然估计(MLE)**。EM 算法的核心思想就像是"先猜后改":因为不知道隐变量,所以先猜隐变量的分布(E步),再根据猜的结果更新模型参数(M步),如此循环直到收敛。
这也是 HMM 模型进行无监督学习(Baum-Welch 算法)时的核心数学基础。
一、 直观理解:EM 解决什么问题?
举个经典的抛硬币例子来理解:
- 简单场景(无隐变量):
假设你有硬币 A,抛了10次,结果是正正反正...。
- 任务: 求 A 正面朝上的概率 。
- 解法: 直接统计正面的次数除以总次数即可。这是直接的最大似然估计。
- 困难场景(有隐变量):
假设你有两枚硬币 A 和 B,它们的偏向不同。你随机拿出一枚抛了一组,又随机拿出一枚抛了一组...总共 5 组数据。
- 数据:
(正正反...), (反反正...), ... - 缺失信息(隐变量): 你不知道每一组数据到底是用 A 抛的,还是用 B 抛的。
- 任务: 求 A 和 B 分别正面朝上的概率。
- 解法: 这就是 EM 算法的用武之地。
二、 EM 算法的详细步骤
假设我们有:
- 观测数据 (你能看见的,如抛硬币结果)。
- 隐变量 (你看不见的,如是哪枚硬币)。
- 模型参数 (你想求的,如硬币的偏向概率)。
我们的目标是最大化似然函数 。
Step 0: 初始化
随机初始化模型参数 。
- 例子: 随便猜硬币 A 的概率是 0.6,B 的概率是 0.5。
Step 1: E步 - 期望步
核心逻辑: 固定当前的参数 ,根据观测数据 ,计算隐变量 的后验概率分布。或者更准确地说,计算Q函数(对数似然函数的期望)。
- 通俗解释(填补缺失数据):
既然我们有了当前的参数 (比如 A=0.6, B=0.5),我们就可以算出每一组数据"更像是 A 抛的"还是"更像是 B 抛的"。 - 我们不直接说"这是A"或"这是B",而是计算一个概率权重(例如:第一组数据 70% 可能是 A,30% 可能是 B)。
- 这一步相当于把缺失的隐变量 用它的期望值补全了。
Step 2: M步 - 最大化步
核心逻辑: 固定刚刚算出的隐变量分布(或 Q 函数),重新调整参数 ,使得似然函数最大化。
- 通俗解释(重新估计参数):
现在我们假设 E 步算出的"权重"就是事实。 - 根据这些加权的观测数据,重新计算硬币 A 和 B 的正面概率。
- 比如,既然第一组数据"70%是A",那么第一组里的正面次数就有 70% 归功于 A。把所有组归功于 A 的次数加起来,除以总次数,就得到了新的 A 的参数 。
Step 3: 收敛检查
重复执行 E步 和 M步。
每次迭代,似然函数的值都会增加(或不变)。当参数 的变化量小于设定的阈值 ,或者似然函数不再显著增加时,停止迭代。
三、 图解 EM 算法原理
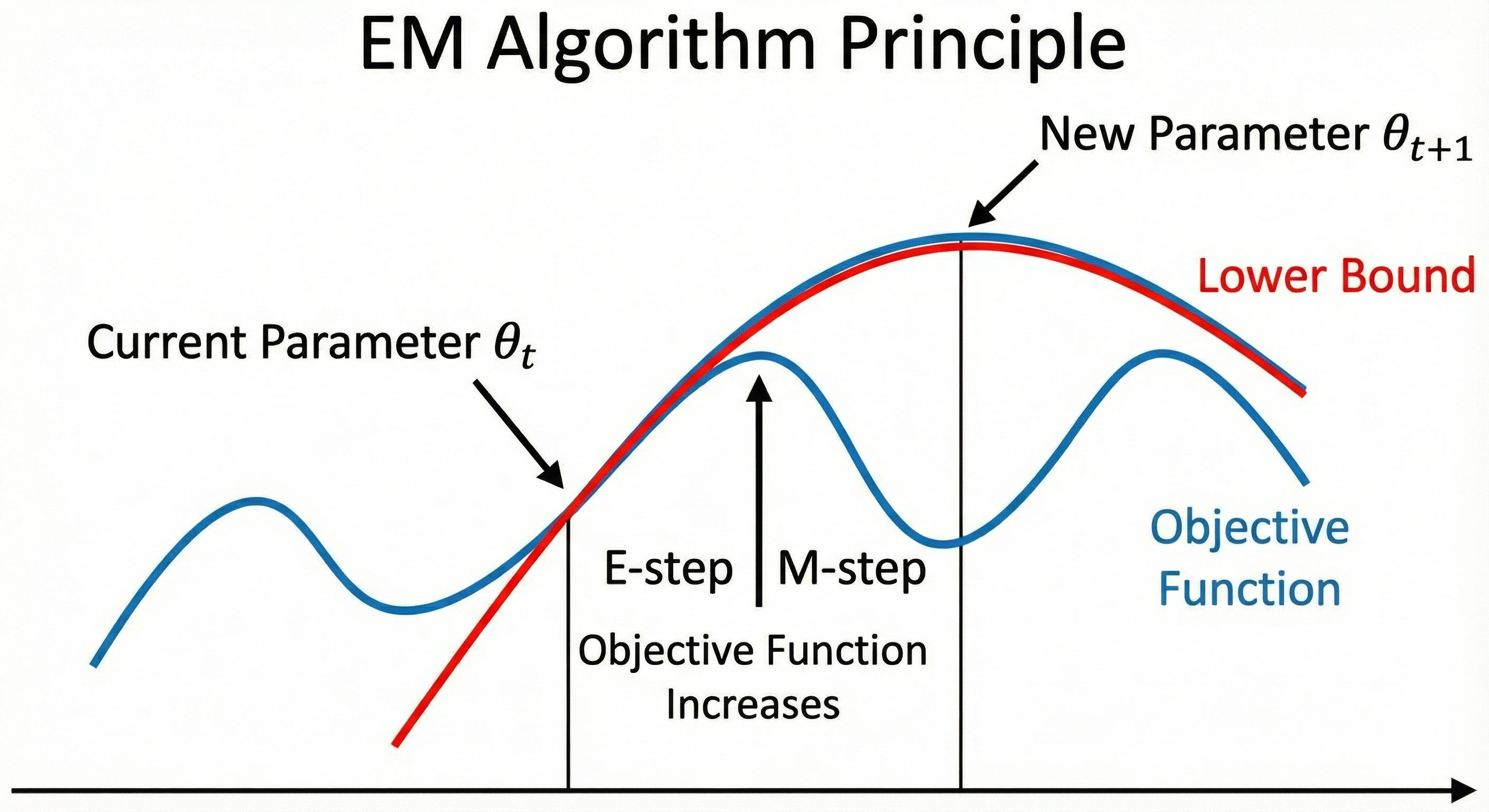
为了更好地理解数学原理,可以参考上面的图示概念:
- 目标函数(蓝色曲线)通常是非凸的,很难直接求极值。
- E步 :构建一个下界函数(Lower Bound,图中的红色曲线),使其在当前点 与目标函数相切。这利用了 Jensen 不等式。
- M步:找到这个下界函数的最高点,作为新的参数 。
- 因为下界函数被推高了,目标函数的值也随之上升。
四、 优缺点总结
-
优点:
-
算法简单稳定,保证似然函数值在每次迭代中非递减。
-
把复杂的含有隐变量的优化问题,转化为一系列简单的无隐变量的优化子问题。
-
缺点:
-
局部最优: EM 算法容易陷入局部最优解(Local Optima),结果非常依赖于初始值 的选择。
-
速度慢: 在某些高维数据上收敛速度可能较慢。