隐马尔科夫模型与条件随机场
核心主题: 序列标注、隐马尔科夫模型(HMM)、CRF对比、大模型与结构化数据(StructGPT)
第一部分:知识图谱基础
评价指标------ 常考点
-
混淆矩阵:TP (真阳), FP (假阳), FN (假阴), TN (真阴)。
-
基本指标:
-
准确率 (Precision) :选出的项中有多少是正确的?P=TP/(TP+FP)P = TP / (TP + FP)P=TP/(TP+FP)
-
召回率 (Recall) :正确的项中有多少被选出了?R=TP/(TP+FN)R = TP / (TP + FN)R=TP/(TP+FN)
-
F1值 (F-measure):P和R的调和平均数,综合指标。
F1=2×P×RP+RF1 = \frac{2 \times P \times R}{P + R}F1=P+R2×P×R
-
-
NER的特殊性 :只有当边界 和 类型 都预测正确时,才算正确(TP)。
第二部分:序列标注与隐马尔科夫模型
I. 序列标注问题
- 输入 :观测序列 X1:T=(x1,x2,...,xT)X_{1:T} = (x_1, x_2, ..., x_T)X1:T=(x1,x2,...,xT) (如:一句话的单词)
- 输出 :标签序列 Y1:T=(y1,y2,...,yT)Y_{1:T} = (y_1, y_2, ..., y_T)Y1:T=(y1,y2,...,yT) (如:对应的词性或实体标签)
- 经典方法 :
- 简单分类器 (Simple Classification)
- 隐马尔科夫模型 (HMM) ------ 生成式模型
- 条件随机场 (CRF) ------ 判别式模型
II.隐马尔可夫模型 (HMM)
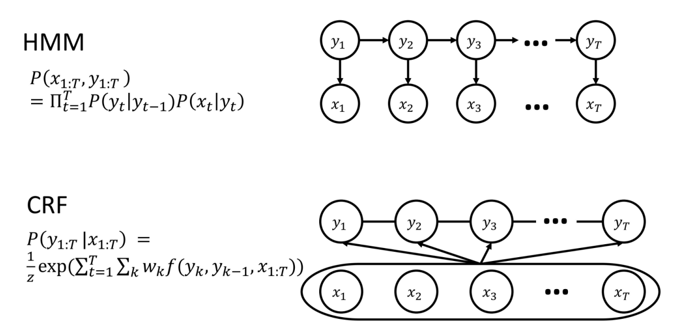
HMM 是图片上半部分展示的模型。它是一种生成式模型。
1. 概率图解读
- 结构: 有向图。
- 节点:
- yty_tyt :代表隐藏状态,例如词性标注中的"名词"、"动词"。
- xtx_txt:代表观测变量,例如句子中的具体单词。
- 箭头含义 (依赖关系):
- yt−1→yty_{t-1} \rightarrow y_tyt−1→yt:表示马尔可夫假设 。当前的状态仅依赖于前一个状态。这对应了转移概率。
- yt→xty_t \rightarrow x_tyt→xt:表示独立输出假设。当前的观测值仅取决于当前的状态。这对应了**发射概率。
2. 公式解读
P(x1:T,y1:T)=∏t=1TP(yt∣yt−1)P(xt∣yt) P(x_{1:T}, y_{1:T}) = \prod_{t=1}^{T} P(y_t | y_{t-1}) P(x_t | y_t) P(x1:T,y1:T)=t=1∏TP(yt∣yt−1)P(xt∣yt)
- P(x1:T,y1:T)P(x_{1:T}, y_{1:T})P(x1:T,y1:T) :HMM 对联合概率分布建模。它试图描述"观测序列和状态序列同时出现的概率是多少"。
- ∏\prod∏ (连乘):因为假设了独立性,整个序列的概率被分解为每一步概率的乘积。
- P(yt∣yt−1)P(y_t | y_{t-1})P(yt∣yt−1):状态转移概率(如:名词后面接动词的概率)。
- P(xt∣yt)P(x_t | y_t)P(xt∣yt):发射概率(如:名词这个词性生成单词"苹果"的概率)。
3.隐马尔科夫模型 (HMM) 五元组
HMM 由五个要素 λ=(Q,A,O,B,π)\lambda = (Q, A, O, B, \pi)λ=(Q,A,O,B,π) 描述:
- QQQ:状态集合(NNN个隐藏状态,如词性标签)。
- AAA:状态转移概率矩阵 (aija_{ij}aij) ------ 从状态 iii 转移到状态 jjj 的概率。
- OOO:观测序列。
- BBB:发射概率 (Emission Probability) (bj(ot)b_j(o_t)bj(ot)) ------ 在状态 jjj 下生成观测值 oto_tot 的概率。
- π\piπ:初始状态概率分布。
4. HMM 的两个重要假设 (必背)
-
马尔科夫假设 :当前状态只依赖于前一个状态。
P(qi∣q1...qi−1)=P(qi∣qi−1)P(q_i | q_1...q_{i-1}) = P(q_i | q_{i-1})P(qi∣q1...qi−1)=P(qi∣qi−1)
-
输出独立性假设 :当前的观测值只依赖于当前的状态。
P(oi∣q1...qT,o1...oT)=P(oi∣qi)P(o_i | q_1...q_T, o_1...o_T) = P(o_i | q_i)P(oi∣q1...qT,o1...oT)=P(oi∣qi)
5. HMM 的三个核心问题
问题 1:概率计算
- 目标 :给定模型 λ\lambdaλ 和观测序列 OOO,计算 P(O∣λ)P(O|\lambda)P(O∣λ)。
- 难点 :直接枚举所有可能的状态序列极其复杂 (NTN^TNT)。
- 算法 :前向算法 。
- 思想:动态规划。定义 αt(j)\alpha_t(j)αt(j) 为时刻 ttt 到达状态 jjj 且观测到前 ttt 个符号的概率。
- 递推公式:αt(j)=∑i=1Nαt−1(i)aijbj(ot)\alpha_t(j) = \sum_{i=1}^N \alpha_{t-1}(i) a_{ij} b_j(o_t)αt(j)=∑i=1Nαt−1(i)aijbj(ot)。
- 最终结果:∑i=1NαT(i)\sum_{i=1}^N \alpha_T(i)∑i=1NαT(i)。
问题 2:解码 (Decoding)
- 目标 :给定模型 λ\lambdaλ 和观测序列 OOO,找到最可能的隐藏状态序列 QQQ。
- 算法 :维特比算法 (Viterbi Algorithm) 。
- 思想:动态规划。定义 vt(j)v_t(j)vt(j) 为时刻 ttt 到达状态 jjj 的最大路径概率。
- 递推公式:vt(j)=maxi=1N(vt−1(i)aij)bj(ot)v_t(j) = \max_{i=1}^N (v_{t-1}(i) a_{ij}) b_j(o_t)vt(j)=maxi=1N(vt−1(i)aij)bj(ot)。
- 关键:需要记录路径回溯指针 (Backpointer) 以还原路径。
问题 3:学习 (Learning)
- 目标 :给定观测序列 OOO,估计模型参数 λ=(A,B,π)\lambda = (A, B, \pi)λ=(A,B,π)。
- 算法 :前向-后向算法 (Forward-Backward Algorithm) (也称为 Baum-Welch 算法)。
- 思想:EM 算法(期望最大化)的一种特例。
- 利用前向概率 α\alphaα 和后向概率 β\betaβ 来估计在时刻 ttt 处于状态 iii 的期望次数,从而更新参数。
6. HMM前向算法示例
①场景设定 (HMM 的基本要素)
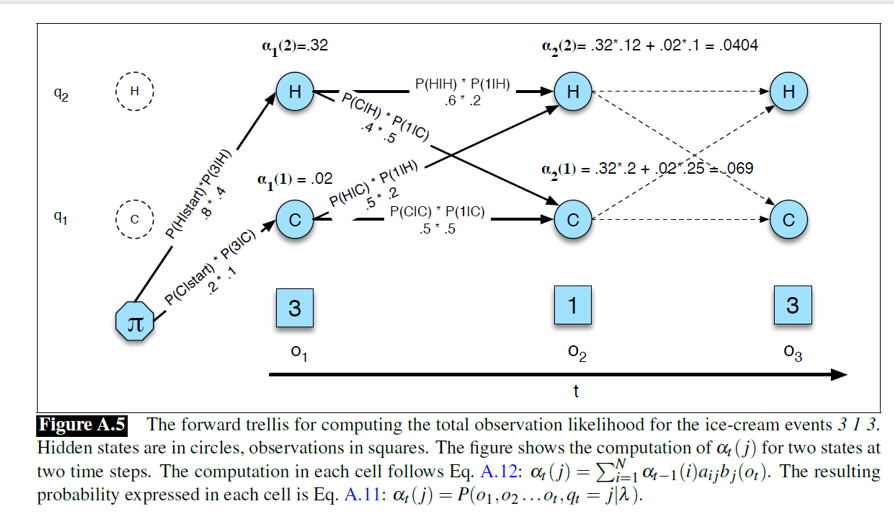
- 观测序列 ( OOO) :这是我们已知的数据。图片中显示的观测序列是 3, 1, 3。意思是第一天吃了 3 个,第二天吃 1 个,第三天吃 3 个。
- 隐状态 (Hidden States, QQQ) :这是导致观测结果背后的原因,但我们看不见。这里有两个状态:Hot (热) 和 Cold (冷)。
- 模型参数 :
- 初始概率 (π\piπ) :P(Hot∣start)=0.8P(Hot|start) = 0.8P(Hot∣start)=0.8, P(Cold∣start)=0.2P(Cold|start) = 0.2P(Cold∣start)=0.2。
- 转移概率 (aija_{ij}aij) :
- 热 →\to→ 热:0.60.60.6,热 →\to→ 冷:0.40.40.4
- 冷 →\to→ 热:0.50.50.5,冷 →\to→ 冷:0.50.50.5
- 发射概率 (bj(ot)b_j(o_t)bj(ot)) (即在某种天气下吃 xxx 个冰淇淋的概率):
- 天热吃 3 个的概率 P(3∣H)=0.4P(3|H) = 0.4P(3∣H)=0.4,吃 1 个的概率 P(1∣H)=0.2P(1|H) = 0.2P(1∣H)=0.2。
- 天冷吃 3 个的概率 P(3∣C)=0.1P(3|C) = 0.1P(3∣C)=0.1。
② 问题的提出:似然度计算 (Likelihood Computation)
目标 :我们需要计算出观测到序列 "3, 1, 3" 的总概率 P(O)P(O)P(O)。
-
如果我们假设天气的变化序列是确定的,比如 "热 -> 热 -> 冷",那么计算概率很简单。
P(3,1,3 AND H,H,C)=P(路径)×P(观测∣路径) P(3,1,3 \text{ AND } H,H,C) = P(\text{路径}) \times P(\text{观测}|\text{路径}) P(3,1,3 AND H,H,C)=P(路径)×P(观测∣路径)这只是计算了一条路径的联合概率。
-
但实际上,我们不知道天气序列是什么。可能是 "热热冷",也可能是 "冷冷热",或者 "热冷热"。要得到 P(3,1,3)P(3, 1, 3)P(3,1,3) 的总概率,最笨的方法是把 所有可能的天气排列组合(NTN^TNT 种,这里是 23=82^3=823=8 种)都算一遍,然后加起来。公式:P(O)=∑QP(O,Q)P(O) = \sum_Q P(O, Q)P(O)=∑QP(O,Q)。问题:当序列变长时,计算量呈指数级爆炸,实际上无法完成。
③解决方案:前向算法
核心思想是动态规划。不要等到最后才求和,而是每走一步就汇总一次概率。我们定义一个变量 αt(j)\alpha_t(j)αt(j),表示"在时刻 ttt,观测到前面的序列并且停留在状态 jjj"的概率。
核心计算过程: 
第一步:时间 t=1t=1t=1 (观测值 o1=3o_1=3o1=3)
需要计算第一天是热天且吃3个的概率,以及第一天是冷天且吃3个的概率。
-
热 (α1(2)\alpha_1(2)α1(2)):
初始概率×发射概率=0.8×P(3∣Hot)=0.8×0.4=0.32初始概率 \times 发射概率 = 0.8 \times P(3|Hot) = 0.8 \times 0.4 = \mathbf{0.32}初始概率×发射概率=0.8×P(3∣Hot)=0.8×0.4=0.32
-
冷 (α1(1)\alpha_1(1)α1(1)):
初始概率×发射概率=0.2×P(3∣Cold)=0.2×0.1=0.02初始概率 \times 发射概率 = 0.2 \times P(3|Cold) = 0.2 \times 0.1 = \mathbf{0.02}初始概率×发射概率=0.2×P(3∣Cold)=0.2×0.1=0.02
第二步:时间 t=2t=2t=2 (观测值 o2=1o_2=1o2=1)
需要计算第二天是"热"且观测到"1"的概率(α2(2)\alpha_2(2)α2(2))。这可以通过两条路径到达:
-
昨天热 →\to→ 今天热:
昨天热的概率(0.32)×保持热的转移概率(0.6)×今天热吃1个的概率(0.2)=0.32×0.6×0.2=0.0384 昨天热的概率 (0.32) \times 保持热的转移概率 (0.6) \times 今天热吃1个的概率 (0.2)= 0.32 \times 0.6 \times 0.2 = 0.0384 昨天热的概率(0.32)×保持热的转移概率(0.6)×今天热吃1个的概率(0.2)=0.32×0.6×0.2=0.0384 -
昨天冷 →\to→ 今天热:
昨天冷的概率(0.02)×变热的转移概率(0.5)×今天热吃1个的概率(0.2)=0.02×0.5×0.2=0.002 昨天冷的概率 (0.02) \times 变热的转移概率 (0.5) \times 今天热吃1个的概率 (0.2)= 0.02 \times 0.5 \times 0.2 = 0.002 昨天冷的概率(0.02)×变热的转移概率(0.5)×今天热吃1个的概率(0.2)=0.02×0.5×0.2=0.002
汇总得到 α2(Hot)\alpha_2(Hot)α2(Hot):
α2(2)=0.0384+0.002=0.0404 \alpha_2(2) = 0.0384 + 0.002 = \mathbf{0.0404} α2(2)=0.0384+0.002=0.0404
同理计算第二天是"冷"的概率 α2(1)\alpha_2(1)α2(1),如图所示为 0.0690.0690.069。
第三步:时间 t=3t=3t=3 (观测值 o3=3o_3=3o3=3)
(图片未展示详细计算,但逻辑相同)
利用 t=2t=2t=2 算出的 α\alphaα 值,乘以转移概率和 t=3t=3t=3 的发射概率,再次求和。
④ 算法总结
-
可视化原理:
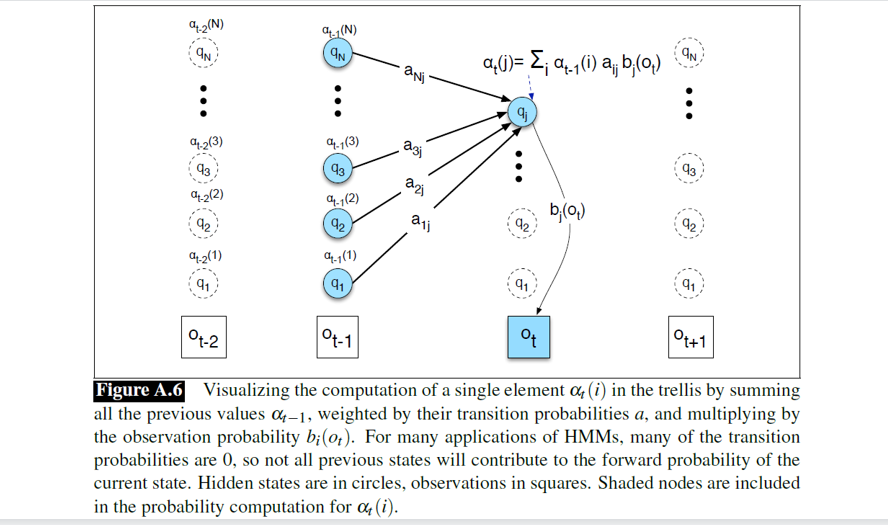
图片展示了 αt(j)\alpha_t(j)αt(j) 是如何通过汇总前一时刻所有状态 αt−1(i)\alpha_{t-1}(i)αt−1(i) 的贡献得来的,即(前一时刻的概率和×转移概率)×当前时刻的发射概率(前一时刻的概率和 \times 转移概率)\times当前时刻的发射概率(前一时刻的概率和×转移概率)×当前时刻的发射概率,公式为αt(j)=[∑iαt−1(i)×aij]×bj(ot)\alpha_t(j) = [\sum_i \alpha_{t-1}(i) \times a_{ij}] \times b_j(o_t)αt(j)=[∑iαt−1(i)×aij]×bj(ot)。
-
伪代码:
- 初始化 :计算 t=1t=1t=1 的 α\alphaα 值。
- 递归 :从 t=2t=2t=2 到 TTT,循环计算每个时刻每个状态的 α\alphaα 值。
- 终止 :把最后时刻 TTT 所有状态的 α\alphaα 值加起来,就是最终的观测概率 P(O)P(O)P(O)。

7.HMM前向-后向算法例题(Baum-Welch 算法)
①简单情况,监督学习
假设我们不仅知道杰森每天吃了多少冰淇淋(观测值),还确切地知道那天的天气(隐状态)。


在这种情况下,计算参数非常简单,就是数数(统计频次):
-
计算初始概率 π\piπ:第一天总共出现了 3 次,其中 "hot" 出现了 1 次,"cold" 出现了 2 次。所以 πhot=1/3,πcold=2/3\pi_{hot} = 1/3, \pi_{cold} = 2/3πhot=1/3,πcold=2/3。
-
计算转移矩阵 AAA:要算 P(hot∣hot)P(hot|hot)P(hot∣hot),就看"前一天是热,后一天还是热"的情况发生了几次,除以"前一天是热"的总次数。这是一个简单的除法:2/32/32/3。
-
计算发射矩阵 BBB:要算 P(1∣hot)P(1|hot)P(1∣hot)(天热吃1个的概率),就去数"天热"的所有日子里,有几天吃了1个。
例子中天热一共4次,没吃过1个,所以概率是 000。
但是现实问题要难得多,因为我们根本不知道隐状态(天气)的计数! 我们只有吃冰淇淋的记录。这就是无监督学习。
② 引入"后向概率" (β\betaβ)
为了解决无监督学习问题,我们需要结合"过去"和"未来"的信息。前向算法 (α\alphaα) 告诉了我们"到达当前状态"的概率,现在我们需要定义 后向概率 (β\betaβ) 。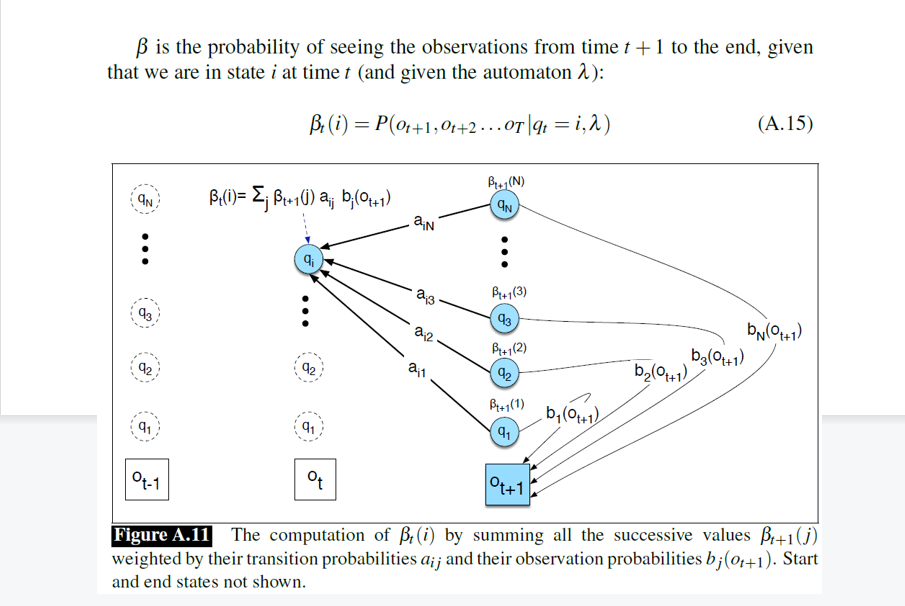
- 定义 :βt(i)\beta_t(i)βt(i) 表示在时刻 ttt 处于状态 iii 的条件下,看到后面剩余所有观测序列 (ot+1...oTo_{t+1} \dots o_Tot+1...oT) 的概率。
- 计算逻辑 :这是一个从后往前的递归过程。
- βt(i)=∑j(转移到j的概率×在j可以看到ot+1的发射概率×从j继续往后的后向概率)\beta_t(i) = \sum_j (\text{转移到}j的概率 \times \text{在}j可以看到o_{t+1}的发射概率 \times \text{从}j继续往后的后向概率)βt(i)=∑j(转移到j的概率×在j可以看到ot+1的发射概率×从j继续往后的后向概率)。
- 公式:βt(i)=∑jaijbj(ot+1)βt+1(j)\beta_t(i) = \sum_j a_{ij} b_j(o_{t+1}) \beta_{t+1}(j)βt(i)=∑jaijbj(ot+1)βt+1(j)。
简单理解:α\alphaα 是从起点推导到现在的累积概率,β\betaβ 是从终点反推回现在的累积概率。
③期望计算(E-Step)
既然不知道具体的天气,我们就用期望 来代替真实的计数。我们需要估算在某个时刻 ttt,从状态 iii 跳转到状态 jjj 的概率有多大。我们定义一个新的变量 ξt(i,j)\xi_t(i, j)ξt(i,j) 。
- 含义 :在已知整个观测序列 OOO 和模型参数 λ\lambdaλ 的情况下,时刻 ttt 处于状态 iii,且时刻 t+1t+1t+1 处于状态 jjj 的概率 。

如何计算 ξt(i,j)\xi_t(i, j)ξt(i,j)?为了连接 ttt 时刻的 iii 和 t+1t+1t+1 时刻的 jjj,我们需要把四部分乘起来:
- αt(i)\alpha_t(i)αt(i) :怎么走到 iii 的(前向概率)。
- aija_{ij}aij :从 iii 跳到 jjj 的概率(转移概率)。
- bj(ot+1)b_j(o_{t+1})bj(ot+1) :在 jjj 观测到 ot+1o_{t+1}ot+1 的概率(发射概率)。
- βt+1(j)\beta_{t+1}(j)βt+1(j) :从 jjj 之后会发生什么的概率(后向概率)。

这就得到了 not-quite-ξ\xiξ(未归一化的概率)。为了变成真正的概率,我们需要除以整个观测序列的总概率 P(O∣λ)P(O|\lambda)P(O∣λ)。
④参数更新(M-Step)
1.计算处于某个状态的概率 (γ\gammaγ)
在更新发射概率之前,我们需要知道一个核心信息:在时刻 ttt,我们有多大可能处于状态 jjj? 我们把这个概率记为 γt(j)\gamma_t(j)γt(j) (Gamma)。
-
直观理解:
为了确定 ttt 时刻处于中间那个节点 sjs_jsj 的概率,我们需要综合两方面的信息:
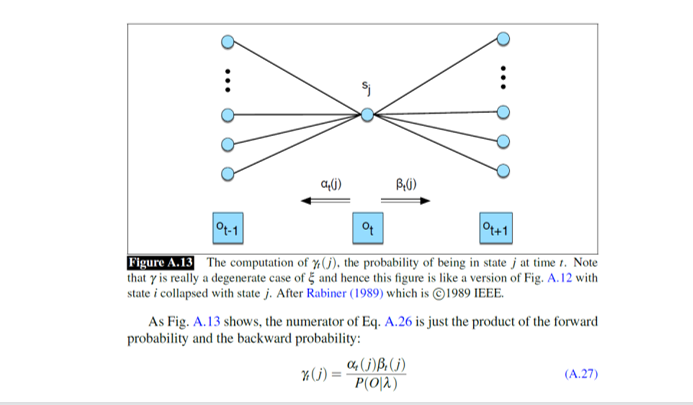
- 来自过去的证据 (αt(j)\alpha_t(j)αt(j)) :根据 ttt 之前发生的所有事情,有多大概率走到这一步?
- 来自未来的证据 (βt(j)\beta_t(j)βt(j)) :如果我们要让 ttt 之后的所有观测都吻合,现在的状态 jjj 必须有多大的可能性?
-
公式含义:
γt(j)=αt(j)βt(j)P(O∣λ) \gamma_t(j) = \frac{\alpha_t(j)\beta_t(j)}{P(O|\lambda)} γt(j)=P(O∣λ)αt(j)βt(j)分子是前向概率和后向概率的乘积,分母是整个观测序列的总概率(用于归一化,确保概率之和为1)。
2. 更新发射概率矩阵 (矩阵 BBB)
有了 γ\gammaγ (我们在每一刻处于状态 jjj 的概率),我们就可以更新 发射概率 b^j(vk)\hat{b}_j(v_k)b^j(vk) 了。也就是要算:如果今天是状态 jjj(比如热天),观测到符号 vkv_kvk(比如吃3个冰淇淋)的概率是多少?
-
计算逻辑:这是一个加权平均的过程:
-
分子:∑t=1 s.t. Ot=vkTγt(j)\sum_{t=1 \text{ s.t. } O_t=v_k}^T \gamma_t(j)∑t=1 s.t. Ot=vkTγt(j)
我们要把所有时刻 ttt 遍历一遍。如果时刻 ttt 的观测值正好是我们关心的 vkv_kvk(比如"吃3个"),我们就把这一刻处于状态 jjj 的概率 γt(j)\gamma_t(j)γt(j) 加进去。
(翻译:在所有"吃3个"的日子里,有多大比例是"热天"?)
-
分母:∑t=1Tγt(j)\sum_{t=1}^T \gamma_t(j)∑t=1Tγt(j)
这是所有时刻处于状态 jjj 的概率之和。
(翻译:总共有多少个期望的"热天"?)
两者相除,就得到了新的 P(吃3个∣热)P(\text{吃3个}|\text{热})P(吃3个∣热)。
-

3. 算法总览:前向-后向算法 (Baum-Welch)
算法分为两个步骤循环进行,直到收敛(参数不再剧烈变化):
-
E-step (期望步):
- 我们假设当前的参数 AAA 和 BBB 是对的。
- 利用前向(α\alphaα)和后向(β\betaβ)算法,计算出两个关键的"期望统计量":
- γt(j)\gamma_t(j)γt(j):时刻 ttt 处于状态 jjj 的概率。
- ξt(i,j)\xi_t(i, j)ξt(i,j):时刻 ttt 从 iii 跳到 jjj 的概率。
-
M-step (最大化步):
- 利用 E-step 算出来的 γ\gammaγ 和 ξ\xiξ,重新估算(更新)模型参数:
- 更新 a^ij\hat{a}_{ij}a^ij :用 ξ\xiξ 之和除以 γ\gammaγ 之和(算转移概率)。
- 更新 b^j(vk)\hat{b}_j(v_k)b^j(vk) :用特定观测的 γ\gammaγ 之和除以总 γ\gammaγ 之和(算发射概率)。
- 利用 E-step 算出来的 γ\gammaγ 和 ξ\xiξ,重新估算(更新)模型参数:
-
循环:
得到新的 AAA 和 BBB 后,回到 E-step,算得更准的 γ\gammaγ 和 ξ\xiξ,如此往复。
III、 条件随机场 (CRF)
CRF 是图片下半部分展示的模型,通常指的是线性链 CRF 。它是一种判别式模型。
1. 概率图解读
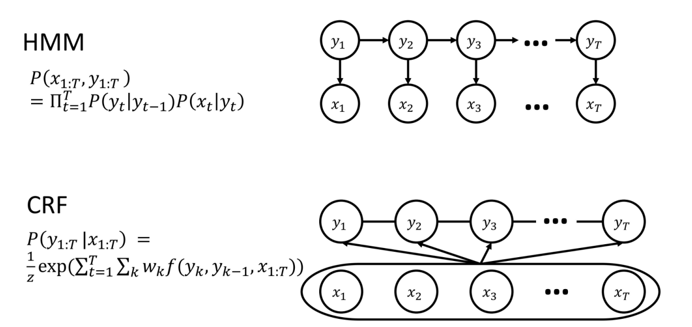
- 结构: 无向图。
- 连接方式:
- yt−1y_{t-1}yt−1 与 yty_tyt 之间有线连接:表示状态之间的相关性。
- 关键区别 :图片底部画了一个大圈框住了所有的 x(x1...xT)x (x_1 ... x_T)x(x1...xT),并且线条从 xxx 区域指向 yyy。这表示 yty_tyt 的判断可以依赖于整个观测序列 x1:Tx_{1:T}x1:T,而不仅仅是当前的 xtx_txt。
2. 公式解读
P(y1:T∣x1:T)=1Zexp(∑t=1T∑kwkf(yk,yk−1,x1:T)) P(y_{1:T} | x_{1:T}) = \frac{1}{Z} \exp\left(\sum_{t=1}^{T} \sum_{k} w_k f(y_k, y_{k-1}, x_{1:T})\right) P(y1:T∣x1:T)=Z1exp(t=1∑Tk∑wkf(yk,yk−1,x1:T))
- P(y1:T∣x1:T)P(y_{1:T} | x_{1:T})P(y1:T∣x1:T) :CRF 对条件概率分布 建模。它直接回答"给定一句话 xxx,标注序列 yyy 是样子的概率最大"。
- 1Z\frac{1}{Z}Z1:归一化因子。因为无向图没有自然的概率解释,需要计算所有可能的路径分数之和来归一化,确保最终结果是一个概率值(0到1之间)。
- exp\expexp & ∑\sum∑:这是对数线性模型的形式。
- wkf(...)w_k f(...)wkf(...) :
- fff 是特征函数 (Feature Function) 。它可以非常灵活,例如:"如果 xtx_txt 是'Apple'且 xt−1x_{t-1}xt−1 是'Eat',则 yty_tyt 倾向于是'名词'"。
- 注意公式里的 x1:Tx_{1:T}x1:T:特征函数可以查看整个句子,不仅限于当前词。
IV、 HMM 与 CRF 的核心对比
| 维度 | HMM (隐马尔可夫模型) | CRF (条件随机场) |
|---|---|---|
| 模型类型 | 生成式模型 (建模联合概率 P(x,y)P(x,y)P(x,y)) | 判别式模型 (建模条件概率 P(y∣xP(y|xP(y∣x) |
| 图结构 | 有向图 (贝叶斯网络) | 无向图 (马尔可夫随机场) |
| 依赖假设 | 强假设 : 1. 观测独立性 (xtx_txt 只依赖 yty_tyt) 2. 齐次马尔可夫性 (yty_tyt 只依赖 yt−1y_{t-1}yt−1) | 弱假设 : 消除了观测独立性假设,状态 yty_tyt 可以依赖于整个观测序列 xxx 以及周边的状态。 |
| 特征能力 | 弱。无法使用复杂的特征(如大小写、词缀、上下文单词组合),因为必须先对 P(x∣yP(x|yP(x∣y 建模。 | 强。可以定义任意复杂的全局特征(Feature Engineering),利用上下文信息。 |
| 归一化 | 局部归一化(每一步概率和为1)。 | 全局归一化 (ZZZ 因子)。这解决了"标记偏置问题 (Label Bias Problem)"。 |
| 优缺点 | 优点 :计算速度快,适合无监督学习。 缺点:特征限制大,准确率通常低于 CRF。 | 优点 :准确率高,特征灵活,克服了 HMM 的独立性限制。 缺点 :训练代价高(计算 ZZZ 需要动态规划),速度慢。 |
- 看图理解本质: HMM 的图强调生成过程 (箭头向下,由状态生成词);CRF 的图强调条件约束(线条相连,状态由整个句子环境共同决定)。
- 演进关系: CRF 可以看作是 HMM 的一种更强大、更灵活的推广。在全监督的序列标注任务(如分词、NER)中,CRF 的表现通常优于 HMM,因为它可以"看见"整句话来做决定,而不是像 HMM 那样"只盯着当前看"。
第三部分:教授的复习建议
- HMM 计算题 :
- 考试极有可能给出一个简单的 HMM 例子(如课件中的"天气-冰淇淋"例子),让你手动模拟 Viterbi 算法 的前两步,或者计算某条路径的概率。
- 公式记忆 :务必记住 HMM 的两个假设公式,以及 αt(j)\alpha_t(j)αt(j) 和 vt(j)v_t(j)vt(j) 的递推公式的区别(一个是求和 ∑\sum∑,一个是求最大值 max\maxmax)。
- 概念辨析 :
- 理解生成式模型 (HMM) 和判别式模型 (CRF) 的本质区别。
- 理解 NER 评价中 F1 值的计算方法,特别是 Precision 和 Recall 的分母分别是"预测出的总数"和"真实存在的总数"。