从传统机器学习固定特征提取器，到深度学习可学习特征 ，模型表达能力实现质的飞跃，
但也带来训练优化、参数设置等一系列挑战。
本文聚焦深度学习核心痛点，从神经网络基础结构 入手，逐步深入优化算法 、参数初始化、
过拟合防治 等关键环节，搭配CNN原理与PyTorch实操示例，理清深度学习训练的底层逻辑，
掌握从理论到实践的核心技能。
目录
[1. 前馈神经网络 FFN](#1. 前馈神经网络 FFN)
[2. 神经网络的潜力 + 训练的问题](#2. 神经网络的潜力 + 训练的问题)
[3. Optimization in DL 非线性优化的难点与好性质](#3. Optimization in DL 非线性优化的难点与好性质)
[4. 参数初始化](#4. 参数初始化)
[5. 防止过拟合](#5. 防止过拟合)
[6. CNN 卷积神经网络](#6. CNN 卷积神经网络)
之前机器学习 特征提取器 是训练前人为设定好的、固定的，
Hand-designed feature 设计还需要 domain knowledge 领域先验知识。
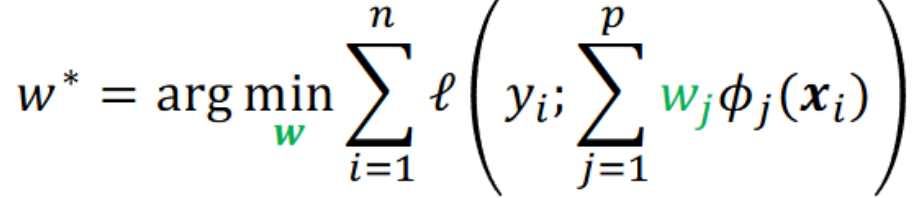
现在特征提取函数 φ 也设置参数可以学。
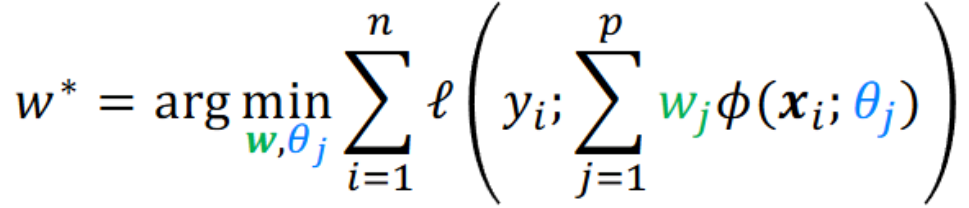
激活函数（为模型引入非线性，大大增强了模型的表达能力）的一般要求：
-
单调递增 2. 连续可导 3. 导函数的值域要在一个合适的区间内
-
激活函数和导函数尽量简单；提高网络计算效率
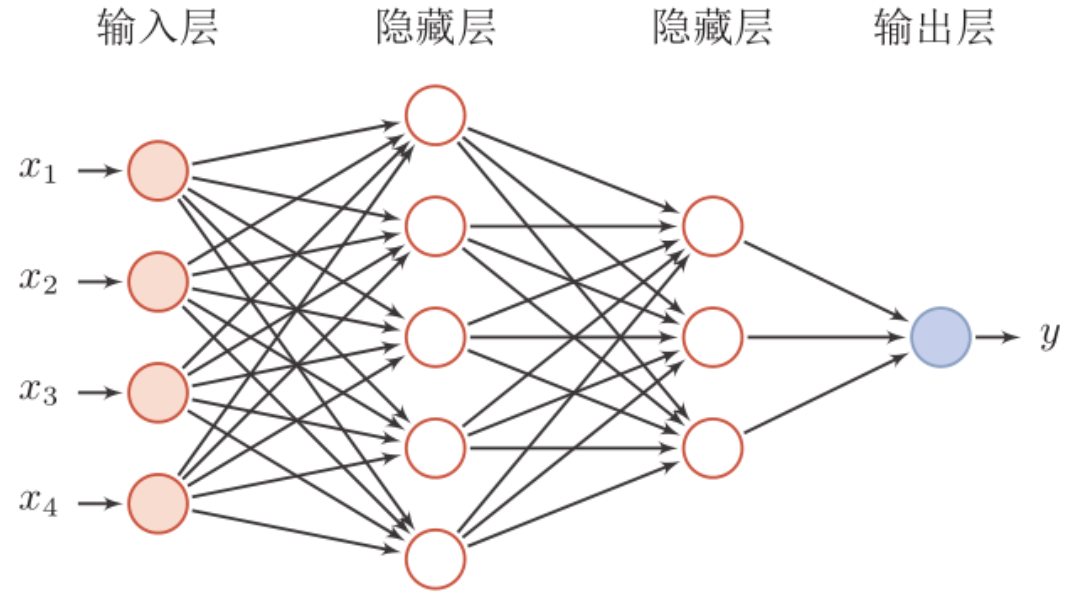
1. 前馈神经网络 FFN
- 各神经元分别属于不同的层，层内无连接。
- 相邻两层 之间的神经元全部两两连接。
- 信号从输入层向输出层单向传播。
例：XOR 异或问题 ；传统方法无法一条线分割。
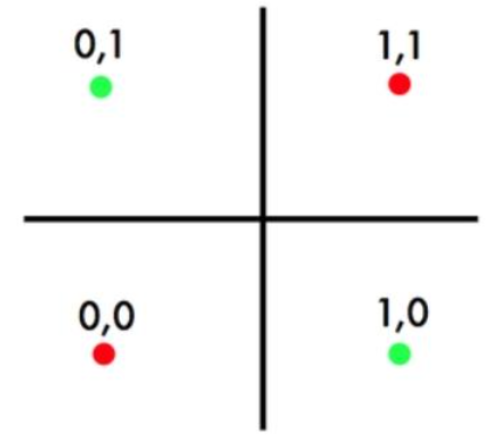共四种情况。
网络的参数架构：（激活函数 ReLU） W，b = [ 后一层维度 * 前一层维度 ]
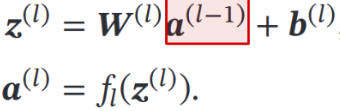
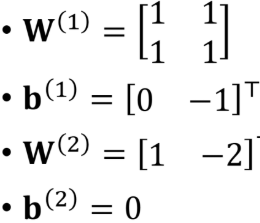
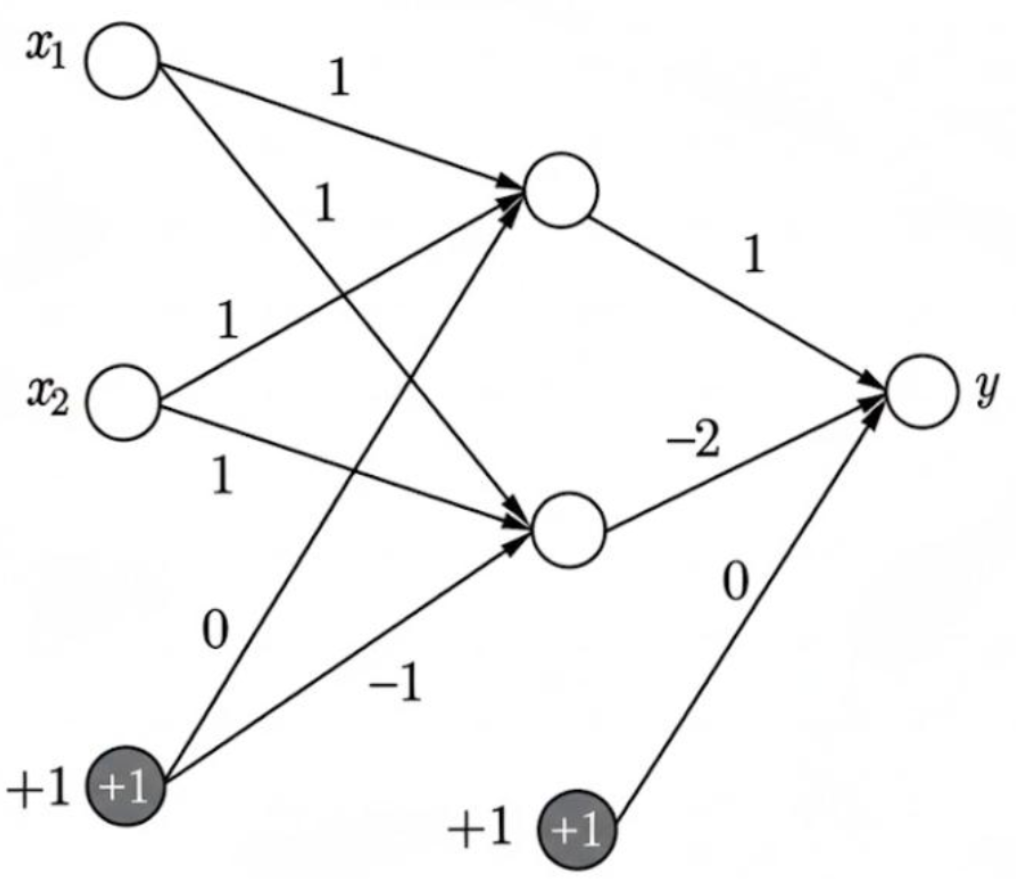
对四种情况的 X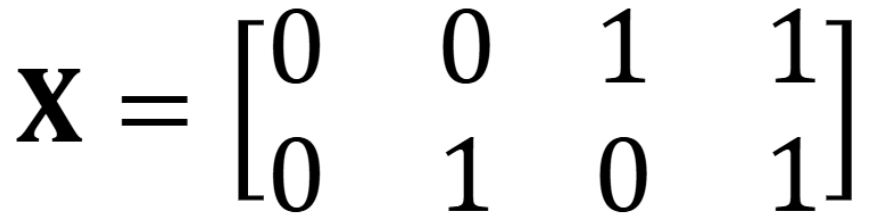 
结果分别为 0,1,1,0
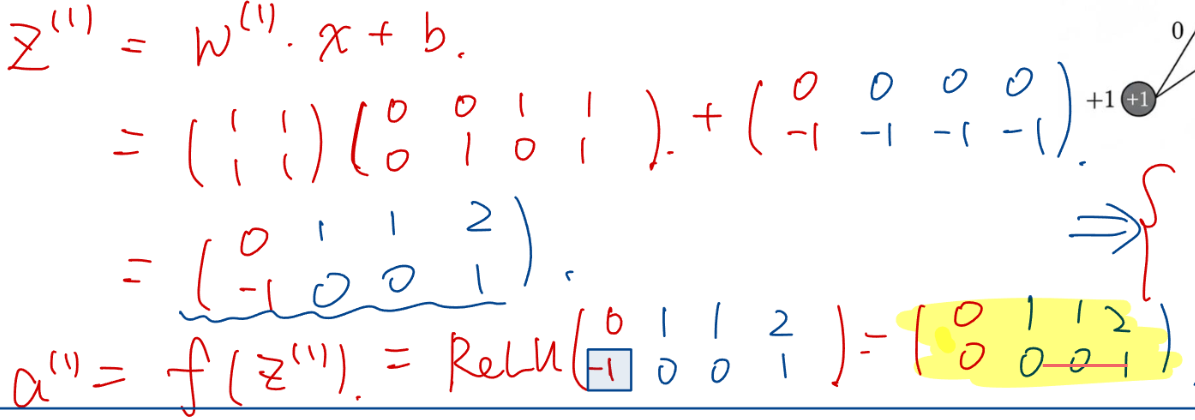
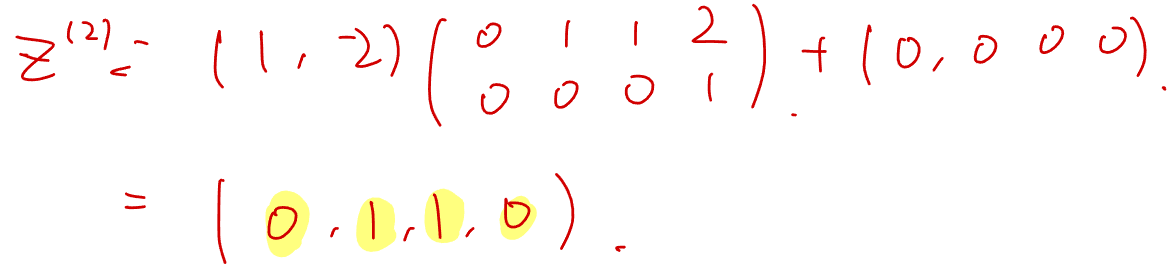
2. 神经网络的潜力 + 训练的问题
通用近似定理 -> 神经网络的潜力
只要其隐藏层神经元的数量足够 ，则可以以任意的精度来近似任何 实数空间中的有界闭集函数。
（简要证明：构建两个神经元A,B 分别在a,b 处由0跳变到1；
A-B 则得到一个矩形脉冲；再由无数个这样的脉冲近似 每个x都调到对应的y）
问题：理论存在 ≠ 现实可行（可以找到）
（1）训练可能陷入局部最优 、可能过拟合 、可能需要海量数据。
（2）这种两层网络的 hidden layer 神经元个数可能很大，训练困难
增大层数→ 深度神经网络（Deep NeuralNetwork）；
划分区间更多 + 参数量更多 => 表达能力更强。
端到端（end-to-end）：特征提取和分类器 设计整体优化；直接输入层到结果层。
问题：如何更新 参数？如何选择超参数 ？（层数，神经元个数，学习率，激活函数）如何防止过拟合？
更新参数：对损失函数计算梯度 Backpropagation 反向传播
链式法则求导 -> 先前馈计算结果，再反向计算梯度
Computation Graph 计算图
3. Optimization in DL 非线性优化的难点与好性质
坏消息：容易陷入局部最小（大部分稳定点都是鞍点），无通用解法。 但有两个好性质：
性质1：深度学习的损失曲面虽然非凸，但局部最优之间是连通的 ------
意味着即使训练陷入某个局部最优，这个点的性能也不会太差；
两个训练好的模型参数按比例混合，得到新模型可能效果更好（低成本实现 "集成"）
性质2：SGD 的随机噪声 + 扰动梯度下降 （Perturbed GD）可以高效逃离鞍点。
- 优化算法：用 SGD 的变体（Adam、RMSprop 等）提升效率
- 超参数 / 初始化 ：调学习率、批次大小，用更好的初始化（如 He/Kaiming 初始化）
- 网络结构 ：设计更 "友好" 的损失曲面（如残差网络 ResNet，缓解梯度消失）
- 硬件：用 GPU/TPU 加速计算
Kimi-K2：MuonClip
4. 参数初始化
错误初始化的例子：如果某些神经元（或权重矩阵）在初始化时是完全对称的，
那么在训练中，它们会始终保持对称 ，无法被训练区分，导致网络无法"打破对称性"，
网络退化成多个重复单元。
避免 梯度消失 / 爆炸 、以及激活值分布失控的问题：
- 如果各层激活值的方差逐层缩小 → 激活值会趋近于 0（梯度消失，模型难以训练）；
- 如果方差逐层放大 → 激活值会变得极大（梯度爆炸，模型参数更新失控）。
目标：初始化权重时，要满足两个关键条件：
- 激活值的均值接近 0；
- 激活值的方差在每一层都保持一致。
根据 M 每层的神经元个数，根据损失函数 选取两种初始化。
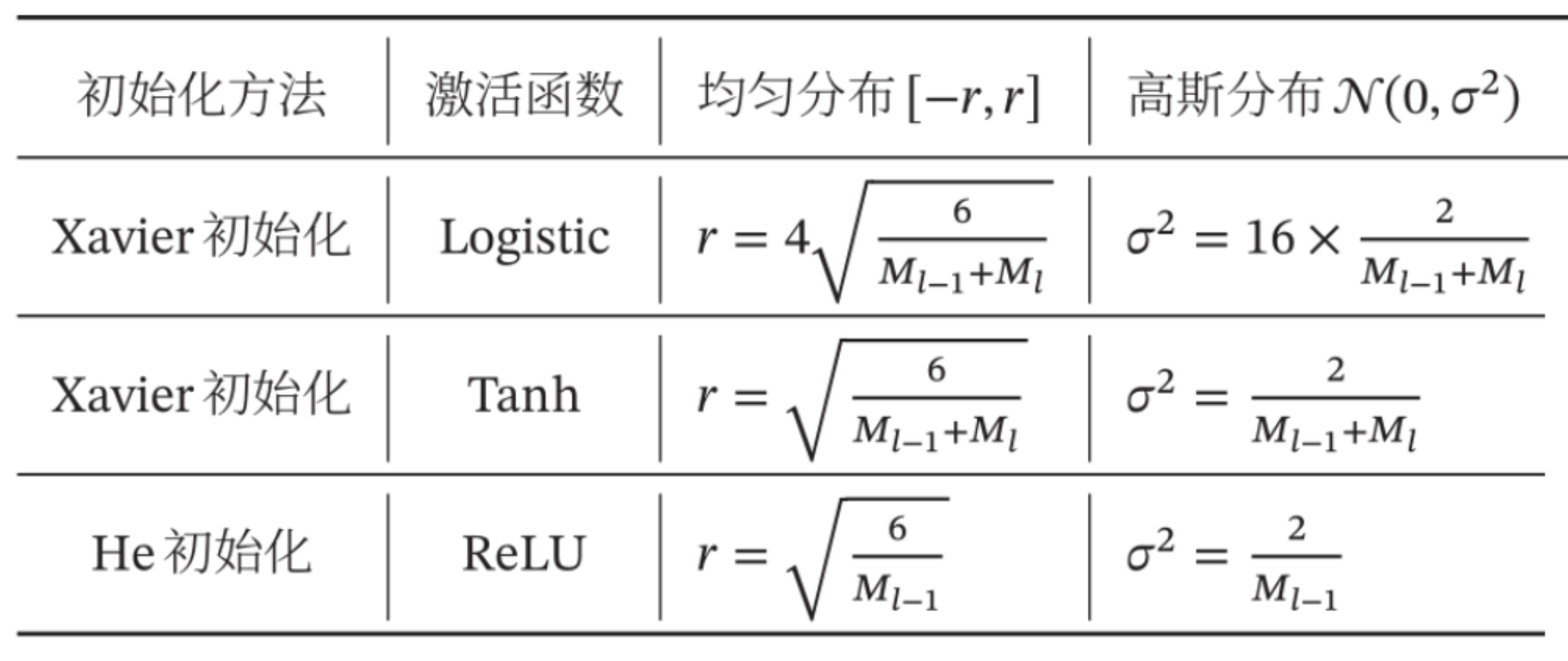
Logistic/Tanh 这类 "对称、输出范围有限" 的激活函数，考虑输入加输出 Xavier初始化
ReLU系列（一半神经元会 "失活"）只考虑输入层 神经元数 He 初始化
5. 防止过拟合
pytorch 需要 model.train() 和 model.eval() 切换模式，训练和测试时 下列做法会不一样。
- Weight decay（权重衰减 ）每次参数更新时，引入一个衰减系数
如 Adam -> AdamW
- Dropout 随机丢弃一些神经元（类似 bagging）
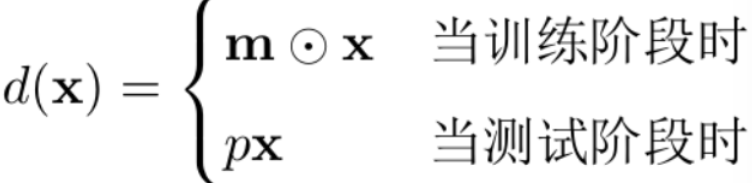
训练 时，每个 batch 都会随机 "关掉" 一部分神经元（相当于从原网络中随机抽取一个 "子网络"）
测试 时不丢弃神经元，但会把所有神经元的输出乘以 "保留概率p"，
相当于对所有训练过的子网络的预测结果做平均集成。
-
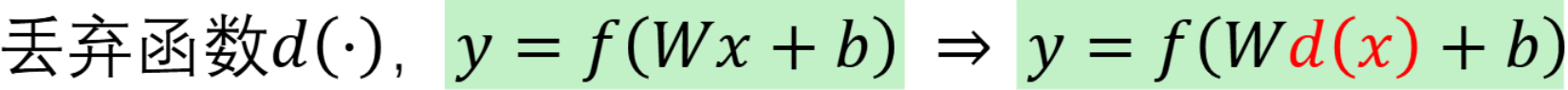
Early stopping 早停
-
Batch Normalization BN 批量归一化
训练时：
测试时：
使用全局统计量 ：不再计算当前 batch 的统计量，直接用训练阶段跟踪得到的
6. CNN 卷积神经网络
局部不变性 尺度缩放、平移、旋转等操作不影响其语义信息。
卷积层 代替全连接层；利用 感受野（Receptive Field）机制 处理图像。
-
局部连接：每个神经元只看"附近的像素"。
-
权重共享：同一个kernel参数应用在图像的每个位置
（从而降低训练参数量）
- 空间或时间上的次采样（汇聚） -> 池化
一维卷积在信号处理，计算信号的延迟累积；输入信号序列 x 和滤波器 w，
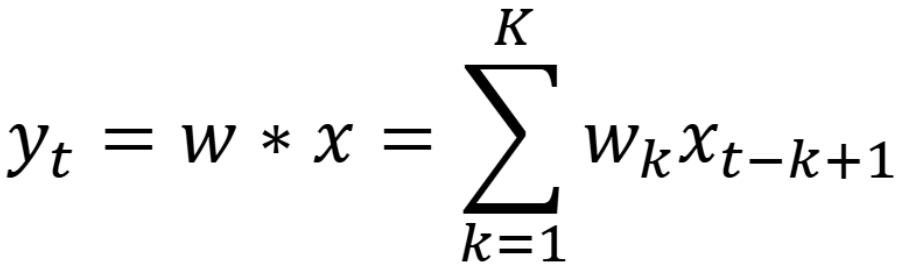
对应相乘求和
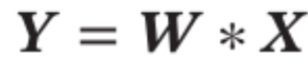
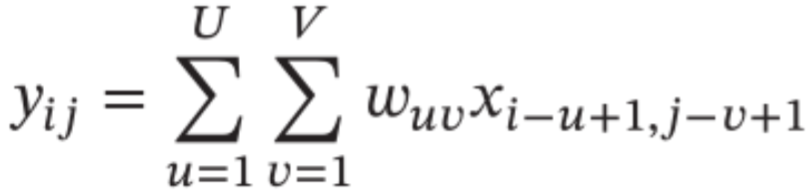
卷积拓展 • 引入滤波器的滑动步长S (stride) 和零填充P (zero padding)
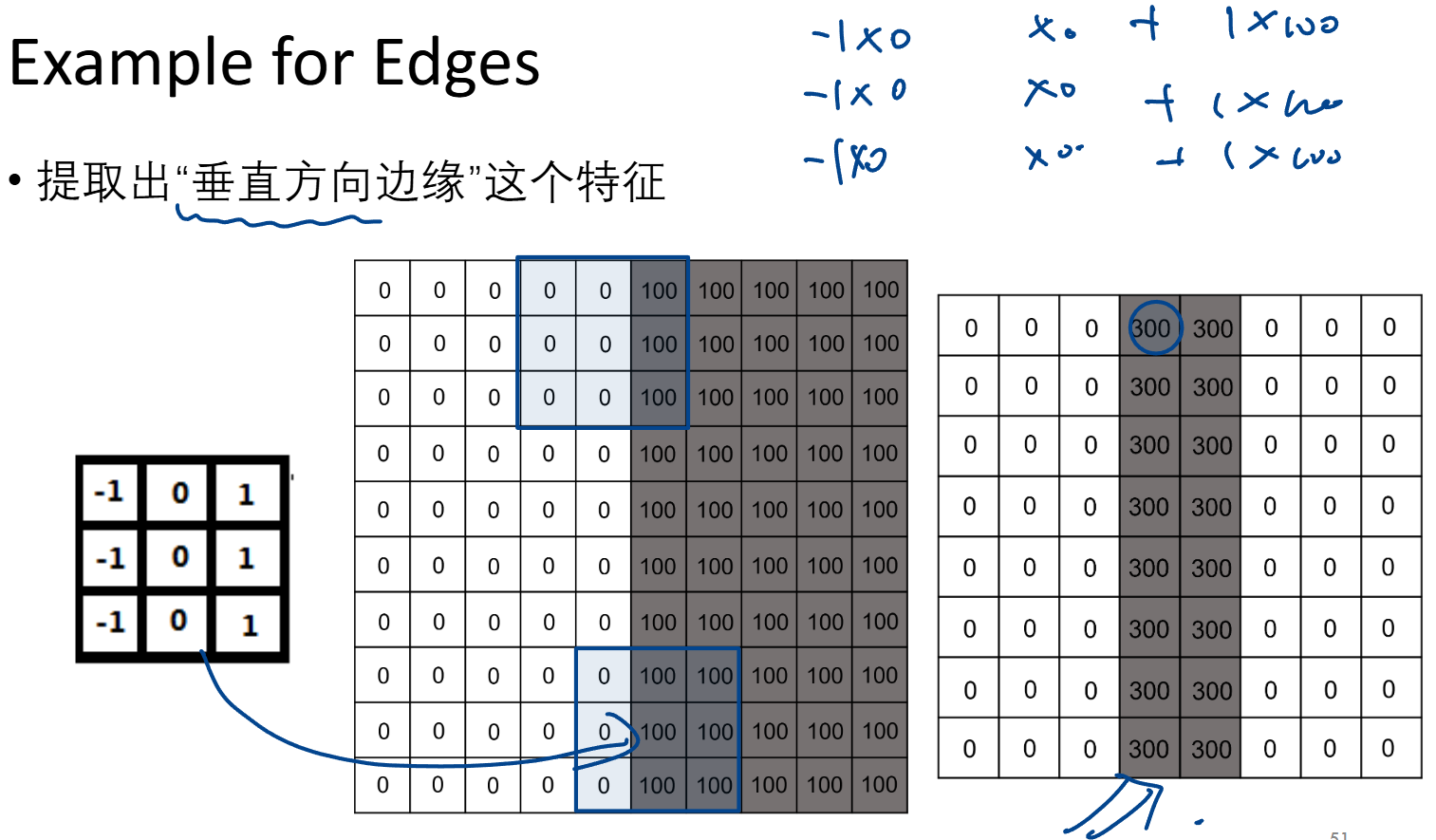
不同卷积核 适用于提取不同特征（下例为 提取一个竖直的墙）
https://docs.pytorch.org/vision/main/models
torchvision - resnet50 的例子
python
from torchvision.io import decode_image
from torchvision.models import resnet50, ResNet50_Weights
# 1. 加载图像
img = decode_image("test/assets/encode_jpeg/grace_hopper_517x606.jpg")
# 2. 初始化模型并加载最佳预训练权重
weights = ResNet50_Weights.DEFAULT # 获取最佳预训练权重
model = resnet50(weights=weights) # 创建ResNet50模型并加载权重
model.eval() # 设置为评估模式（关闭Dropout等训练专用层）
# 3. 初始化与权重匹配的预处理转换
preprocess = weights.transforms() # 获取与该权重匹配的预处理函数（包含标准化等操作）
# 4. 对图像应用预处理并添加批次维度
batch = preprocess(img).unsqueeze(0) # 应用预处理转换并增加批次维度 [1,C,H,W] 第一维维batch大小 因为单个图片
# 5. 模型推理并计算概率分布
prediction = model(batch).squeeze(0).softmax(0) # 前向传播，移除批次维度，应用softmax得到概率
# 6. 解析预测结果
class_id = prediction.argmax().item() # 获取最高概率的类别ID
score = prediction[class_id].item() # 获取对应的置信度分数
category_name = weights.meta["categories"][class_id] # 从元数据获取类别名称
# 7. 输出分类结果
print(f"{category_name}: {100 * score:.1f}%") # 输出格式示例："military uniform: 96.5%"卷积层为 Conv2d(in, out, kernel, stride, padding)
输入为 (batch, in, h, w) 输出为 (batch, out, h, w)
python
m = nn.Conv2d(16, 33, (3, 5), stride=(2, 1), padding=(4, 2))
input = torch.randn(20, 16, 50, 100)
output = m(input)