目录
[1. 引言](#1. 引言)
[2. 回归评估指标的基础理论](#2. 回归评估指标的基础理论)
[2.1 回归问题的本质与误差的来源](#2.1 回归问题的本质与误差的来源)
[2.2 评估指标的分类与选择原则](#2.2 评估指标的分类与选择原则)
[3. 四个关键评估指标的理论基础](#3. 四个关键评估指标的理论基础)
[3.1 平均绝对误差(MAE)](#3.1 平均绝对误差(MAE))
[3.2 均方误差(MSE)和均方根误差(RMSE)](#3.2 均方误差(MSE)和均方根误差(RMSE))
[3.3 决定系数(R²)](#3.3 决定系数(R²))
[4. 四个指标的侧重点与应用场景深度分析](#4. 四个指标的侧重点与应用场景深度分析)
[4.1 不同业务场景下的指标选择](#4.1 不同业务场景下的指标选择)
[4.2 多指标评估的最佳实践](#4.2 多指标评估的最佳实践)
[5. 完整项目实现:房价预测模型的全面评估](#5. 完整项目实现:房价预测模型的全面评估)
[5.1 数据集介绍与模型训练](#5.1 数据集介绍与模型训练)
[5.2 交叉验证与模型稳定性评估](#5.2 交叉验证与模型稳定性评估)
[6. 指标选择与应用的实践指南](#6. 指标选择与应用的实践指南)
[7. 总结与最佳实践](#7. 总结与最佳实践)
1. 引言
在机器学习和深度学习的实际应用中,模型的优劣不仅取决于其复杂度或参数数量,更关键的是它在真实数据上的预测性能。对于回归问题,如房价预测、股票价格预估、需求量预测等,建立了模型之后,如何科学、全面地评估模型的性能就成为了必须解决的问题。不同的评估指标从不同的角度反映了模型预测结果与真实值之间的差异,理解这些指标的含义、计算方法和应用场景,对于机器学习工程师进行模型选择、参数调优和业务决策具有至关重要的意义。
当我们训练了一个回归模型来预测某个连续值目标变量时,会自然地产生一个问题:这个模型的预测准确性究竟如何?我的预测值与真实值相差多远?这个差异是否可接受?如果有多个模型可选,我应该选择哪一个?这些问题的答案都依赖于我们对各种评估指标的深刻理解。平均绝对误差(Mean Absolute Error, MAE)、均方误差(Mean Squared Error, MSE)、均方根误差(Root Mean Squared Error, RMSE)和决定系数(Coefficient of Determination, R²)是回归模型评估中最常用的四个指标,它们各有特点,在不同的业务场景中有着不同的应用价值。
本文将系统地介绍这四个评估指标的数学原理,阐述它们各自的侧重点和适用场景,通过完整的代码实现从零开始构建这些指标的计算方法,最后通过一个真实房价预测项目的完整案例,展示如何在实际中运用这些指标来评估和对比不同的回归模型。通过这个过程,你将获得对回归模型评估的全面、深入的理解,这对于进行数据科学工作和机器学习项目有着直接的指导意义。
2. 回归评估指标的基础理论
2.1 回归问题的本质与误差的来源
回归分析是一种统计学方法,用于建立因变量与一个或多个自变量之间的关系模型。在机器学习的背景下,回归问题指的是预测一个连续值的问题。当我们有了一个训练好的回归模型后,它会对新的输入进行预测,产生一个预测值。然而,由于各种原因(如模型复杂度不足、数据噪声、特征不完整等),预测值往往与真实值之间存在差异,我们称之为预测误差或残差。理解误差的来源是评估模型性能的前提。一般来说,回归模型的总误差可以分为三个部分:偏差(Bias)、方差(Variance)和噪声(Noise)。偏差反映的是模型的假设与真实情况之间的差异,如果我们使用了过于简单的模型来拟合复杂的数据分布,就会产生较大的偏差。方差反映的是模型对数据波动的敏感程度,一个过于复杂的模型可能会过度拟合训练数据,导致在测试数据上的方差较大。噪声则是数据本身固有的随机性,无法通过模型改进来消除。评估指标的作用就是通过量化这些误差,帮助我们理解模型的性能水平。
在实际应用中,我们通常会在独立的测试集或验证集上计算评估指标。这是因为训练集上的指标往往不能反映模型在未来新数据上的真实性能,而在测试集上的指标才能更真实地反映模型的泛化能力。随着机器学习的发展,交叉验证技术也被广泛应用,通过多次划分数据集并计算平均的评估指标来获得更稳定和可靠的性能估计。
2.2 评估指标的分类与选择原则
回归评估指标可以从不同的角度进行分类。从计算逻辑来看,有基于误差绝对值的指标(如MAE)和基于误差平方的指标(如MSE、RMSE);从指标的含义来看,有衡量预测偏离程度的指标(MAE、MSE、RMSE)和衡量模型整体拟合优度的指标(R²)。理解这些分类有助于在实际应用中做出合适的选择。选择合适的评估指标需要考虑多个方面。首先是业务背景,不同的业务问题对误差的容忍度不同。例如,在医疗诊断中,过高的预测值(预测病人病情较重)可能比过低的预测值(预测病人病情较轻)更危险,这时就需要选择能够惩罚特定方向误差的指标。其次是数据特性,如果数据中存在离群点或异常值,应该选择对离群点鲁棒性更强的指标。再次是模型对比的需求,有时候我们需要的是绝对的误差大小,有时候需要的是相对的性能对比。最后是可解释性的要求,对于需要向非技术人员解释的模型,选择易于理解的指标会更有帮助。
3. 四个关键评估指标的理论基础
3.1 平均绝对误差(MAE)
平均绝对误差是最直观、最易理解的回归评估指标之一。它衡量的是预测值与真实值之间差异的平均水平,其数学定义如下:
MAE = \\frac{1}{n} \\sum_{i=1}\^{n} \|y_i - \\hat{y}_i\|
其中n表示样本总数,y_i表示第i个样本的真实值,\\hat{y}_i表示模型对第i个样本的预测值,|·|表示取绝对值运算。这个公式的含义非常直接:计算每一个样本的预测误差的绝对值,然后求平均。从这个公式可以看出,MAE有几个重要的特性。首先,由于使用了绝对值,无论误差是正的还是负的(即预测值高于还是低于真实值),都被同等对待。这意味着MAE不会因为正误差和负误差的相互抵消而掩盖真实的预测性能。其次,MAE的量纲与目标变量的量纲相同,如果预测的是房价,MAE的单位就是钱,这使得它具有很好的可解释性。第三,MAE对于数据中的离群点(Outliers)具有一定的鲁棒性,因为它不会像平方误差那样放大离群点的影响。
MAE的主要优点包括解释性强、计算简单、对离群点不敏感等。然而,MAE也存在一些局限性,最主要的是MAE在数学性质上不如MSE良好。在优化算法中,MAE的导数是一个符号函数(当误差不为零时为±1),这导致梯度下降等算法在接近最优点时可能会震荡,收敛性不如基于MSE的优化来得稳定。另一个问题是,MAE无法衡量模型的整体拟合优度,它只能告诉我们平均误差的大小,无法说明这个误差是小还是大,是好还是差。
3.2 均方误差(MSE)和均方根误差(RMSE)
均方误差和均方根误差是在机器学习中最常用的损失函数和评估指标。MSE的定义如下:
MSE = \\frac{1}{n} \\sum_{i=1}\^{n} (y_i - \\hat{y}_i)\^2
其中所有符号的含义与MAE相同。MSE的计算过程是:计算每个样本的误差,对其平方,然后求平均。通过平方运算,MSE赋予了较大的误差更多的权重,这意味着模型中的任何异常的大误差都会对MSE产生显著的影响。均方根误差(RMSE)实际上就是MSE的平方根:
RMSE = \\sqrt{MSE} = \\sqrt{\\frac{1}{n} \\sum_{i=1}\^{n} (y_i - \\hat{y}_i)\^2}
引入平方根的目的是为了使RMSE的单位与目标变量相同,从而提高可解释性。这样,RMSE和MAE都具有相同的量纲,但它们的数值往往不同,RMSE的平方根往往大于MAE,因为MSE的平方运算放大了大误差的影响。MSE与RMSE之间的关系非常简单直接:RMSE就是MSE开平方。但这个简单的数学关系背后隐含着重要的统计学意义。当误差符合高斯分布时,RMSE代表了误差分布的标准差的估计。从这个角度看,RMSE可以理解为"典型"的预测误差大小。
MSE和RMSE相比于MAE有几个重要的优势。首先,在数学性质上,MSE作为目标函数时,其导数是一个线性函数(2倍的误差),这使得梯度下降等优化算法能够更加稳定、高效地收敛到最优解。因此,在模型训练过程中,我们通常使用MSE或RMSE作为损失函数。其次,MSE对离群点更加敏感,通过平方运算放大了大误差的影响,这在某些情况下是有益的,因为我们可能希望模型重点关注那些预测失误较大的样本。然而,MSE和RMSE也存在一些局限性,最主要的问题是它们对离群点的过度敏感。如果数据中存在几个异常的离群点,MSE和RMSE可能会被这些点严重影响,导致整体评估指标看起来很差,但实际上模型在大多数数据上的表现还不错。
3.3 决定系数(R²)
决定系数R²是一个衡量回归模型对数据整体拟合程度的指标,它的数学定义如下:
R\^2 = 1 - \\frac{SS_{res}}{SS_{tot}} = \\frac{SS_{reg}}{SS_{tot}}
其中SS_{res} = \\sum_{i=1}\^{n}(y_i - \\hat{y}*i)\^2是残差平方和(Sum of Squares of Residuals),表示实际值与预测值之差的平方和;SS*{tot} = \\sum_{i=1}\^{n}(y_i - \\bar{y})\^2是总平方和(Total Sum of Squares),表示实际值与均值之差的平方和;SS_{reg} = SS_{tot} - SS_{res}是回归平方和(Sum of Squares of Regression),表示模型能够解释的变异。这个公式的核心含义是:R²衡量了因变量的变异中有多大比例被自变量和回归模型所解释。换句话说,它告诉我们模型能够解释因变量总变异的百分比。R²的值域理论上在-∞到1之间,其中1表示完美拟合(所有预测都与真实值一致),0表示模型的拟合效果与简单用均值进行预测一样好,负值表示模型的拟合效果甚至不如用均值进行预测。
理解R²的关键在于认识到它是一个相对的、无量纲的指标。不同于MAE、MSE、RMSE这些绝对误差指标,R²是一个相对指标,它衡量的是模型相对于基线模型(简单使用均值预测)的改进程度。这使得R²特别适合用来比较不同数据集或不同量级数据的模型性能。标准的R²有一个重要的缺陷:当向模型中添加新的自变量时,即使这些变量与因变量无关,R²也总是会增加或保持不变,永远不会减少。这是因为额外的变量总是可以稍微改进对训练数据的拟合,至少可以减少残差平方和。为了解决这个问题,调整的R²(Adjusted R²)被提出:
R_{adj}\^2 = 1 - \\frac{(1-R\^2)(n-1)}{n-p-1}
其中p是模型中自变量的个数,n是样本数。调整R²在标准R²的基础上,考虑了模型的复杂度。每当添加一个新的自变量时,分母会减少1,这会增加惩罚项,使得调整R²只有在新变量能够显著改进模型时才会增加。在特征选择和模型对比中,调整R²比标准R²更加可靠。
4. 四个指标的侧重点与应用场景深度分析
4.1 不同业务场景下的指标选择
四个主要的回归评估指标虽然都旨在衡量模型性能,但它们各自有着不同的侧重点和应用场景。从数学性质看,MAE和RMSE都是绝对误差指标,衡量预测偏离真实值的程度,而R²是一个相对指标,衡量模型相对于基线的改进程度。MSE是优化中常用的损失函数,而RMSE是MSE的平方根,旨在提高可解释性。从对异常值的敏感性看,MAE对异常值最不敏感,因为它只计算绝对偏差;MSE和RMSE对异常值敏感,因为平方会放大大的误差;R²的对异常值的敏感性取决于异常值的方向和程度。从可解释性的角度看,MAE和RMSE都与目标变量有相同的量纲,易于向非技术人员解释;MSE的单位是目标变量的平方,可解释性相对较差;R²是无量纲的,表示模型能解释的变异百分比,具有很强的直观性。
在房价预测中,MAE和RMSE都很重要。如果房价的单位是万元,MAE=10表示平均预测误差为10万元,这是一个非常直观的指标,可以直接用于评估模型的实用价值。RMSE则可以反映预测偏差的波动情况,高RMSE表示有时预测结果偏离较大。R²可以用来说明模型能够解释房价变化的程度,例如R²=0.85表示模型能解释房价变化的85%。在选择不同的房价预测模型时,通常会综合考虑这三个指标。在需求预测中,业务背景变得更加重要。库存过多意味着积压成本,库存过少意味着失销售机会,两者的代价不同。在这种情况下,使用加权的MAE或RMSE会更合适,可以对正误差和负误差赋予不同的权重。如果数据中存在部分销售量特别大的日期(如节假日),这些日期的预测错误会对MSE产生更大的影响,此时使用MAE可能更公平。
在医疗诊断中,如预测患者的病情指数,大的预测错误可能导致医疗决策失误,因此RMSE或加权的RMSE会更合适。如果一个患者的真实病情指数为50,预测为100(高估)和预测为0(低估)的医疗后果可能完全不同,这时需要使用有方向性的误差指标。在金融风险预测中,预测变量往往高度波动。此时,R²可能不会很高(即使模型不错),因为金融数据本身的噪声很大。在这种情况下,RMSE比R²更能反映模型的实际价值,因为它直接衡量了预测精度。在时间序列预测中,不同时间段的预测重要性可能不同。例如,在短期天气预报中,最近一周的预报精度比两周后的预报重要,可以使用时间衰减的权重。此时,加权的MAE或RMSE会比简单的MAE或RMSE更合适。
4.2 多指标评估的最佳实践
在现代机器学习实践中,使用单一指标来评估模型已经不够充分。最佳实践是同时计算和报告多个指标,从不同角度了解模型性能。通常的做法是:首先报告绝对误差指标(MAE和RMSE),直观地说明模型的预测精度;其次报告相对指标(R²),说明模型的整体拟合优度;最后根据业务背景,选择1-2个业务相关的指标。在模型对比时,应该使用相同的测试集计算各个指标,以确保公平性。如果有离群点,应该同时报告含异常值的指标结果和去除异常值后的指标结果,这样可以理解异常值对模型的影响。在交叉验证中,应该对每一折都计算指标,然后报告平均值和标准差,这样可以了解模型性能的稳定性。
5. 完整项目实现:房价预测模型的全面评估
5.1 数据集介绍与模型训练
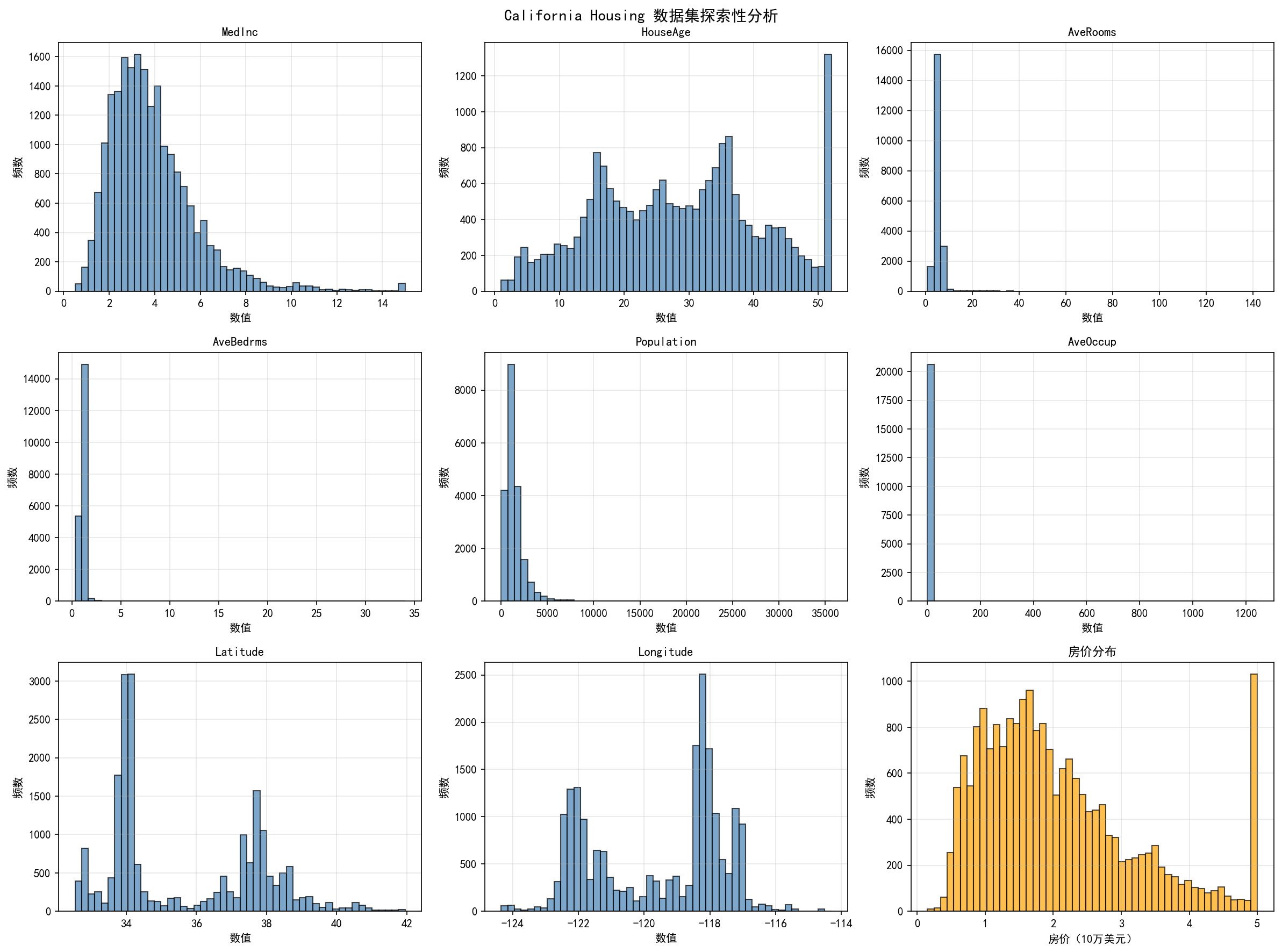
现在我们将使用一个真实的房价数据集来演示如何在实际项目中应用各种回归评估指标。我们使用California Housing数据集,这是一个包含约20000个样本、8个特征的房价预测数据集。这个数据集来自1990年的美国人口普查,包含了加州各地区的房价信息及相关特征。数据集中的特征包括:MedInc(中位数收入)、HouseAge(房屋年龄)、AveRooms(平均房间数)、AveBedrms(平均卧室数)、Population(人口)、AveOccup(平均占用人数)、Latitude(纬度)和Longitude(经度)。目标变量是MedHouseValue(中位房价),单位是10万美元。这个数据集的特点是特征维度适中、样本量充足、数据相对干净,非常适合用来演示回归模型的评估方法。
下面是一个完整的、可直接运行的代码,涵盖了数据加载、探索性分析、多个模型的训练、评估指标的计算以及全面的可视化:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split, cross_val_score, KFold
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, Ridge, Lasso, ElasticNet
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor, AdaBoostRegressor
from sklearn.svm import SVR
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import warnings
warnings.filterwarnings('ignore')
# 修复中文显示问题 - 跨平台兼容方案
import matplotlib
import sys
def setup_chinese_font():
"""
设置matplotlib的中文字体,支持Windows、macOS、Linux
"""
system_font_candidates = {
'Windows': ['SimHei', 'SimSun', 'Microsoft YaHei', 'Arial Unicode MS'],
'Darwin': ['SimHei', 'STHeiti', 'Heiti TC', 'PingFang SC'],
'Linux': ['SimHei', 'DejaVu Sans', 'WenQuanYi Micro Hei']
}
current_system = sys.platform
if current_system.startswith('win'):
system_type = 'Windows'
elif current_system == 'darwin':
system_type = 'Darwin'
else:
system_type = 'Linux'
font_list = system_font_candidates.get(system_type, ['DejaVu Sans'])
# 尝试找到可用的字体
available_fonts = matplotlib.font_manager.findSystemFonts()
available_font_names = [matplotlib.font_manager.FontProperties(fname=font).get_name()
for font in available_fonts]
selected_font = None
for font in font_list:
if font in available_font_names or font in matplotlib.rcParams['font.sans-serif']:
selected_font = font
break
if selected_font is None:
selected_font = font_list[0]
matplotlib.rcParams['font.sans-serif'] = [selected_font, 'DejaVu Sans']
matplotlib.rcParams['axes.unicode_minus'] = False
return selected_font
selected_font = setup_chinese_font()
print(f"使用字体: {selected_font}")
# 加载并分析数据
print("\n" + "="*100)
print("California Housing 数据集加载与分析")
print("="*100)
housing = fetch_california_housing()
X = pd.DataFrame(housing.data, columns=housing.feature_names)
y = pd.Series(housing.target, name='MedHouseValue')
print(f"\n数据集形状: {X.shape}")
print(f"样本数: {len(X)}, 特征数: {X.shape[1]}")
print(f"\n目标变量(房价,单位:10万美元)统计:")
print(f" 均值: ${y.mean()*100000:.2f}")
print(f" 标准差: ${y.std()*100000:.2f}")
print(f" 范围: [${y.min()*100000:.2f}, ${y.max()*100000:.2f}]")
# 绘制数据探索分析图
fig, axes = plt.subplots(3, 3, figsize=(16, 12))
fig.suptitle('California Housing 数据集探索性分析', fontsize=14, fontweight='bold')
feature_names = list(X.columns)
for idx, col in enumerate(feature_names):
row = idx // 3
col_idx = idx % 3
axes[row, col_idx].hist(X[col], bins=50, edgecolor='black', alpha=0.7, color='steelblue')
axes[row, col_idx].set_title(col, fontsize=11)
axes[row, col_idx].set_xlabel('数值')
axes[row, col_idx].set_ylabel('频数')
axes[row, col_idx].grid(True, alpha=0.3)
axes[2, 2].hist(y, bins=50, edgecolor='black', alpha=0.7, color='orange')
axes[2, 2].set_title('房价分布', fontsize=11)
axes[2, 2].set_xlabel('房价(10万美元)')
axes[2, 2].set_ylabel('频数')
axes[2, 2].grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('housing_data_exploration.png', dpi=150, bbox_inches='tight')
print("\n已保存: housing_data_exploration.png")
plt.close()
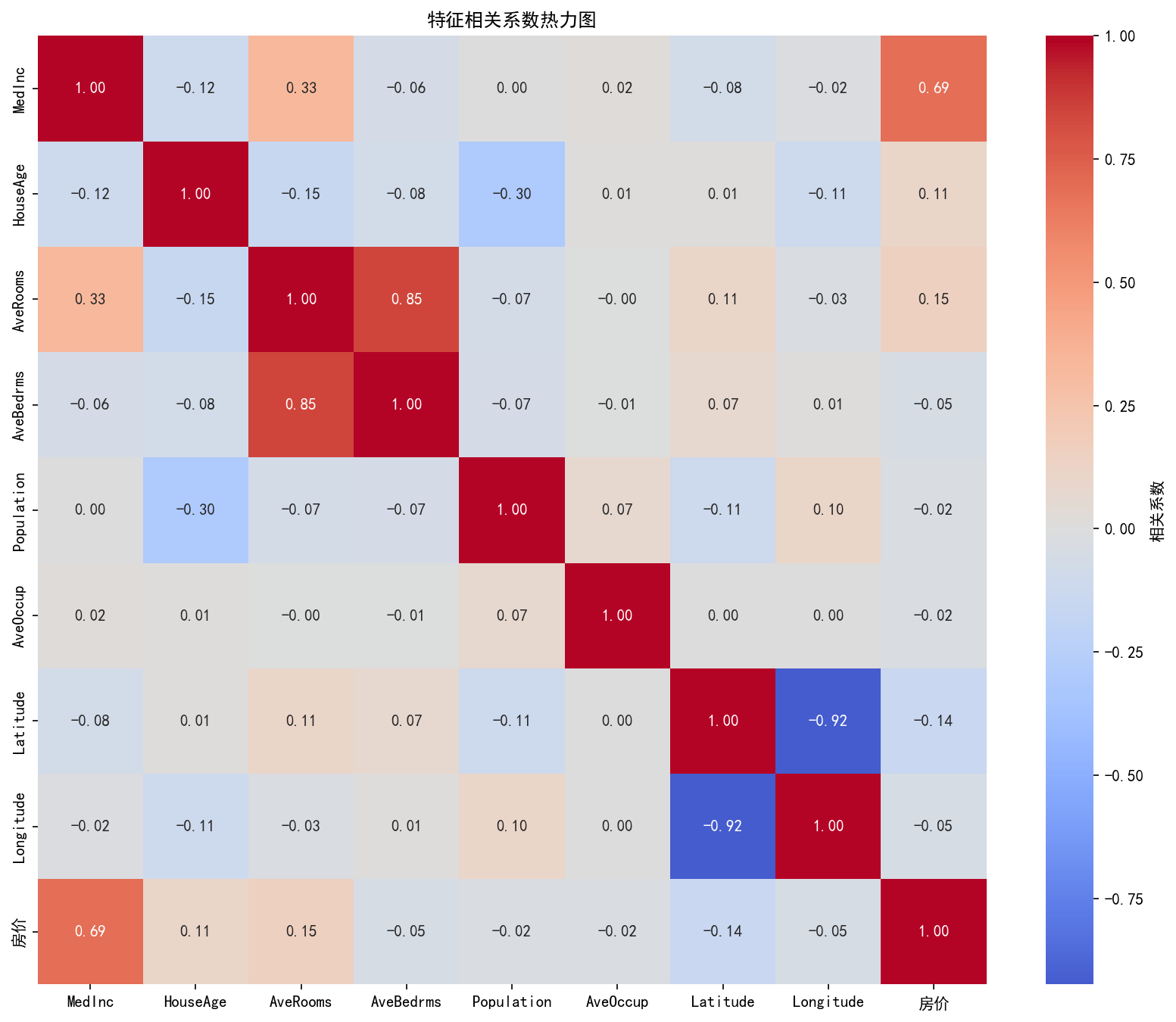
# 相关性分析
print("\n特征与房价的相关系数:")
correlations = X.corrwith(y).sort_values(ascending=False)
for feat, corr in correlations.items():
print(f" {feat:12s}: {corr:7.4f}")
X_with_target = X.copy()
X_with_target['房价'] = y
corr_matrix = X_with_target.corr()
fig, ax = plt.subplots(figsize=(11, 9))
sns.heatmap(corr_matrix, annot=True, fmt='.2f', cmap='coolwarm', center=0,
cbar_kws={'label': '相关系数'}, ax=ax, square=True)
ax.set_title('特征相关系数热力图', fontsize=12, fontweight='bold')
plt.tight_layout()
plt.savefig('housing_correlation_heatmap.png', dpi=150, bbox_inches='tight')
print("已保存: housing_correlation_heatmap.png")
plt.close()
# 数据分割和标准化
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
print(f"\n数据分割:")
print(f" 训练集: {len(X_train)} 样本")
print(f" 测试集: {len(X_test)} 样本")
# 定义和训练多个模型
print("\n" + "="*100)
print("模型训练与评估")
print("="*100)
models_config = [
('线性回归', LinearRegression(), 'scaled'),
('Ridge回归 (α=1.0)', Ridge(alpha=1.0), 'scaled'),
('Lasso回归 (α=0.01)', Lasso(alpha=0.01, max_iter=10000), 'scaled'),
('ElasticNet (α=0.01)', ElasticNet(alpha=0.01, l1_ratio=0.5, max_iter=10000), 'scaled'),
('决策树 (depth=20)', DecisionTreeRegressor(max_depth=20, random_state=42), 'original'),
('随机森林 (n=100)', RandomForestRegressor(n_estimators=100, max_depth=20, n_jobs=-1, random_state=42), 'original'),
('梯度提升 (n=100)', GradientBoostingRegressor(n_estimators=100, max_depth=5, learning_rate=0.1, random_state=42), 'original'),
('AdaBoost (n=100)', AdaBoostRegressor(n_estimators=100, random_state=42), 'original'),
('SVR (RBF)', SVR(kernel='rbf', C=100, gamma='scale'), 'scaled'),
('神经网络', MLPRegressor(hidden_layer_sizes=(128, 64, 32), max_iter=500, early_stopping=True, random_state=42), 'scaled'),
]
metrics_results = {}
model_predictions = {}
for model_name, model, data_type in models_config:
print(f"正在训练: {model_name}...", end=' ')
X_train_use = X_train_scaled if data_type == 'scaled' else X_train.values
X_test_use = X_test_scaled if data_type == 'scaled' else X_test.values
model.fit(X_train_use, y_train)
y_pred_train = model.predict(X_train_use)
y_pred_test = model.predict(X_test_use)
model_predictions[model_name] = (y_pred_train, y_pred_test)
# 计算多个评估指标
train_mae = mean_absolute_error(y_train, y_pred_train)
train_mse = mean_squared_error(y_train, y_pred_train)
train_rmse = np.sqrt(train_mse)
train_r2 = r2_score(y_train, y_pred_train)
test_mae = mean_absolute_error(y_test, y_pred_test)
test_mse = mean_squared_error(y_test, y_pred_test)
test_rmse = np.sqrt(test_mse)
test_r2 = r2_score(y_test, y_pred_test)
test_mape = np.mean(np.abs((y_test - y_pred_test) / y_test)) * 100
test_medae = np.median(np.abs(y_test - y_pred_test))
test_max_error = np.max(np.abs(y_test - y_pred_test))
metrics_results[model_name] = {
'Train MAE': train_mae,
'Train MSE': train_mse,
'Train RMSE': train_rmse,
'Train R²': train_r2,
'Test MAE': test_mae,
'Test MSE': test_mse,
'Test RMSE': test_rmse,
'Test R²': test_r2,
'Test MAPE': test_mape,
'Test MedAE': test_medae,
'Test Max Error': test_max_error,
'Overfitting Gap': train_r2 - test_r2
}
print(f"完成 (Test R²: {test_r2:.4f})")
# 创建详细的结果表
print("\n" + "="*140)
print("模型评估结果总表")
print("="*140)
results_df = pd.DataFrame({
model_name: {
'Train R²': f"{metrics['Train R²']:.4f}",
'Test R²': f"{metrics['Test R²']:.4f}",
'Test MAE': f"{metrics['Test MAE']:.4f}",
'Test RMSE': f"{metrics['Test RMSE']:.4f}",
'Test MAPE': f"{metrics['Test MAPE']:.2f}%",
'过拟合': f"{metrics['Overfitting Gap']:.4f}"
}
for model_name, metrics in metrics_results.items()
}).T
print(results_df.to_string())
# 模型排名
print("\n" + "="*140)
print("模型排名(按测试集R²从高到低)")
print("="*140)
sorted_models = sorted(metrics_results.items(), key=lambda x: x[1]['Test R²'], reverse=True)
for rank, (model_name, metrics) in enumerate(sorted_models, 1):
print(f"{rank:2d}. {model_name:25s} | Test R²: {metrics['Test R²']:.4f} | "
f"Test RMSE: ${metrics['Test RMSE']*100000:8.2f} | "
f"Test MAE: ${metrics['Test MAE']*100000:8.2f} | "
f"过拟合: {metrics['Overfitting Gap']:.4f}")
print("="*140)
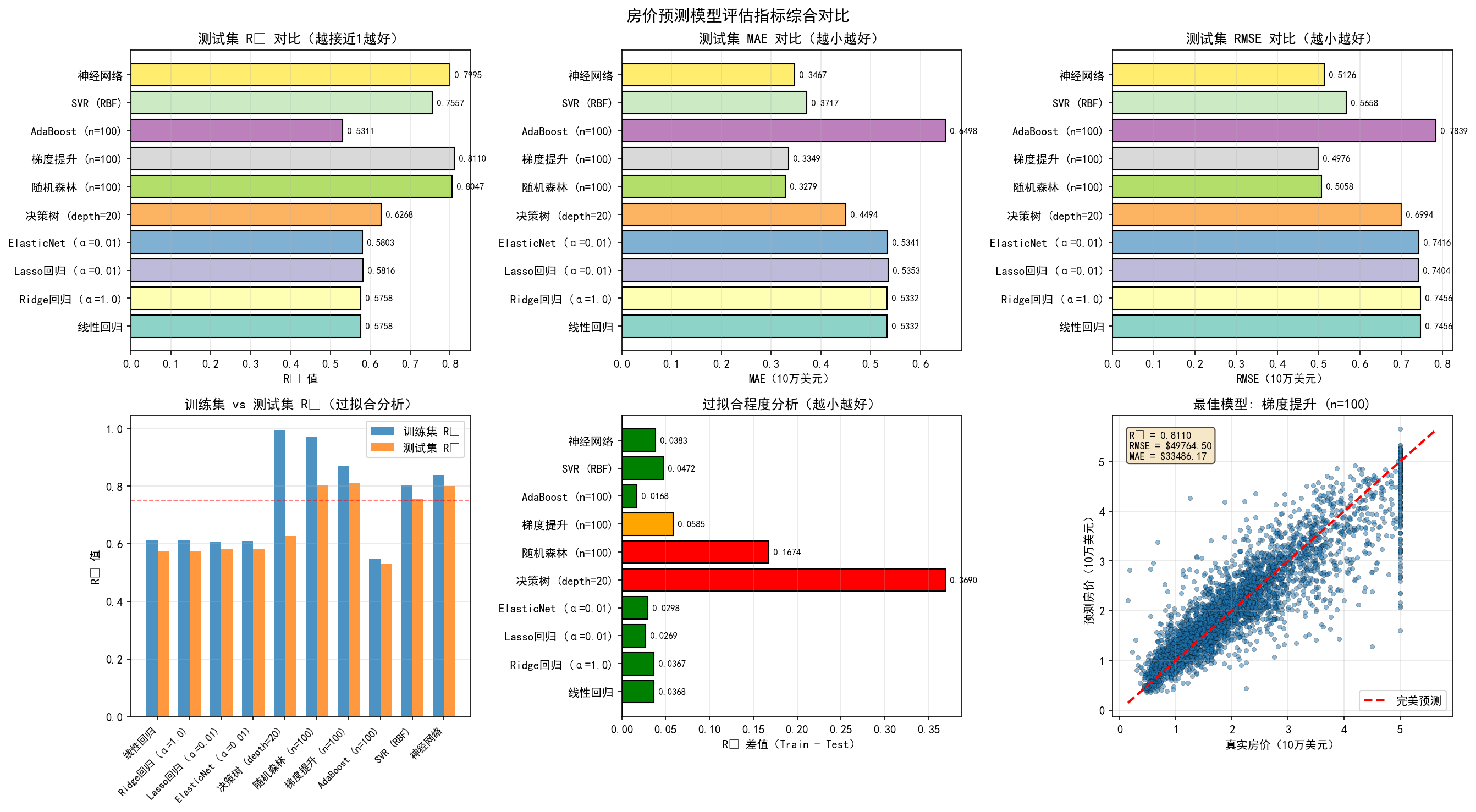
# 绘制综合对比图
fig, axes = plt.subplots(2, 3, figsize=(18, 10))
fig.suptitle('房价预测模型评估指标综合对比', fontsize=14, fontweight='bold')
model_names = list(metrics_results.keys())
colors = plt.cm.Set3(np.linspace(0, 1, len(model_names)))
# 1. Test R² 对比
test_r2_list = [metrics_results[m]['Test R²'] for m in model_names]
axes[0, 0].barh(model_names, test_r2_list, color=colors, edgecolor='black')
axes[0, 0].set_xlabel('R² 值')
axes[0, 0].set_title('测试集 R² 对比(越接近1越好)', fontweight='bold')
axes[0, 0].grid(True, alpha=0.3, axis='x')
for i, v in enumerate(test_r2_list):
axes[0, 0].text(v, i, f' {v:.4f}', va='center', fontsize=8)
# 2. Test MAE 对比
test_mae_list = [metrics_results[m]['Test MAE'] for m in model_names]
axes[0, 1].barh(model_names, test_mae_list, color=colors, edgecolor='black')
axes[0, 1].set_xlabel('MAE(10万美元)')
axes[0, 1].set_title('测试集 MAE 对比(越小越好)', fontweight='bold')
axes[0, 1].grid(True, alpha=0.3, axis='x')
for i, v in enumerate(test_mae_list):
axes[0, 1].text(v, i, f' {v:.4f}', va='center', fontsize=8)
# 3. Test RMSE 对比
test_rmse_list = [metrics_results[m]['Test RMSE'] for m in model_names]
axes[0, 2].barh(model_names, test_rmse_list, color=colors, edgecolor='black')
axes[0, 2].set_xlabel('RMSE(10万美元)')
axes[0, 2].set_title('测试集 RMSE 对比(越小越好)', fontweight='bold')
axes[0, 2].grid(True, alpha=0.3, axis='x')
for i, v in enumerate(test_rmse_list):
axes[0, 2].text(v, i, f' {v:.4f}', va='center', fontsize=8)
# 4. Train vs Test R² 对比
train_r2_list = [metrics_results[m]['Train R²'] for m in model_names]
x = np.arange(len(model_names))
width = 0.35
axes[1, 0].bar(x - width/2, train_r2_list, width, label='训练集 R²', alpha=0.8)
axes[1, 0].bar(x + width/2, test_r2_list, width, label='测试集 R²', alpha=0.8)
axes[1, 0].set_ylabel('R² 值')
axes[1, 0].set_title('训练集 vs 测试集 R²(过拟合分析)', fontweight='bold')
axes[1, 0].set_xticks(x)
axes[1, 0].set_xticklabels(model_names, rotation=45, ha='right', fontsize=9)
axes[1, 0].legend()
axes[1, 0].grid(True, alpha=0.3, axis='y')
axes[1, 0].axhline(y=0.75, color='r', linestyle='--', linewidth=1, alpha=0.5)
# 5. 过拟合程度
overfitting_list = [metrics_results[m]['Overfitting Gap'] for m in model_names]
colors_overfit = ['green' if v < 0.05 else 'orange' if v < 0.1 else 'red' for v in overfitting_list]
axes[1, 1].barh(model_names, overfitting_list, color=colors_overfit, edgecolor='black')
axes[1, 1].set_xlabel('R² 差值(Train - Test)')
axes[1, 1].set_title('过拟合程度分析(越小越好)', fontweight='bold')
axes[1, 1].grid(True, alpha=0.3, axis='x')
axes[1, 1].axvline(x=0, color='k', linestyle='-', linewidth=0.5)
for i, v in enumerate(overfitting_list):
axes[1, 1].text(v, i, f' {v:.4f}', va='center', fontsize=8)
# 6. 最佳模型详细分析
best_model_name = max(metrics_results.items(), key=lambda x: x[1]['Test R²'])[0]
best_predictions_train, best_predictions_test = model_predictions[best_model_name]
best_metrics = metrics_results[best_model_name]
min_val = min(y_test.min(), best_predictions_test.min())
max_val = max(y_test.max(), best_predictions_test.max())
axes[1, 2].scatter(y_test, best_predictions_test, alpha=0.5, s=15, edgecolors='k', linewidth=0.3)
axes[1, 2].plot([min_val, max_val], [min_val, max_val], 'r--', linewidth=2, label='完美预测')
axes[1, 2].set_xlabel('真实房价(10万美元)')
axes[1, 2].set_ylabel('预测房价(10万美元)')
axes[1, 2].set_title(f'最佳模型: {best_model_name}', fontweight='bold')
axes[1, 2].grid(True, alpha=0.3)
axes[1, 2].legend()
info_text = f"R² = {best_metrics['Test R²']:.4f}\nRMSE = ${best_metrics['Test RMSE']*100000:.2f}\nMAE = ${best_metrics['Test MAE']*100000:.2f}"
axes[1, 2].text(0.05, 0.95, info_text, transform=axes[1, 2].transAxes, fontsize=9,
verticalalignment='top', bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.7))
plt.tight_layout()
plt.savefig('housing_model_comparison.png', dpi=150, bbox_inches='tight')
print("\n已保存: housing_model_comparison.png")
plt.close()
# 最佳模型的残差分析
print("\n" + "="*100)
print(f"最佳模型详细分析: {best_model_name}")
print("="*100)
residuals = y_test.values - best_predictions_test
print(f"\n模型性能指标:")
print(f" 训练集 R²: {best_metrics['Train R²']:.6f}")
print(f" 测试集 R²: {best_metrics['Test R²']:.6f}")
print(f" 测试集 MAE: {best_metrics['Test MAE']:.6f} (平均误差: ${best_metrics['Test MAE']*100000:.2f})")
print(f" 测试集 RMSE: {best_metrics['Test RMSE']:.6f} (均方根误差: ${best_metrics['Test RMSE']*100000:.2f})")
print(f" 测试集 MAPE: {best_metrics['Test MAPE']:.2f}%")
print(f" 最大误差: ${best_metrics['Test Max Error']*100000:.2f}")
print(f" 过拟合程度: {best_metrics['Overfitting Gap']:.6f}")
print(f"\n残差分析:")
print(f" 残差均值: {np.mean(residuals):.6f} (理想值为0)")
print(f" 残差标准差: {np.std(residuals):.6f}")
print(f" 残差范围: [{np.min(residuals):.6f}, {np.max(residuals):.6f}]")
mae = best_metrics['Test MAE']
within_1std = np.sum(np.abs(residuals) <= mae) / len(residuals) * 100
within_2std = np.sum(np.abs(residuals) <= 2*mae) / len(residuals) * 100
within_3std = np.sum(np.abs(residuals) <= 3*mae) / len(residuals) * 100
print(f"\n预测精度分析:")
print(f" 误差在 ±${mae*100000:.2f} 范围内的样本: {within_1std:.2f}%")
print(f" 误差在 ±${2*mae*100000:.2f} 范围内的样本: {within_2std:.2f}%")
print(f" 误差在 ±${3*mae*100000:.2f} 范围内的样本: {within_3std:.2f}%")
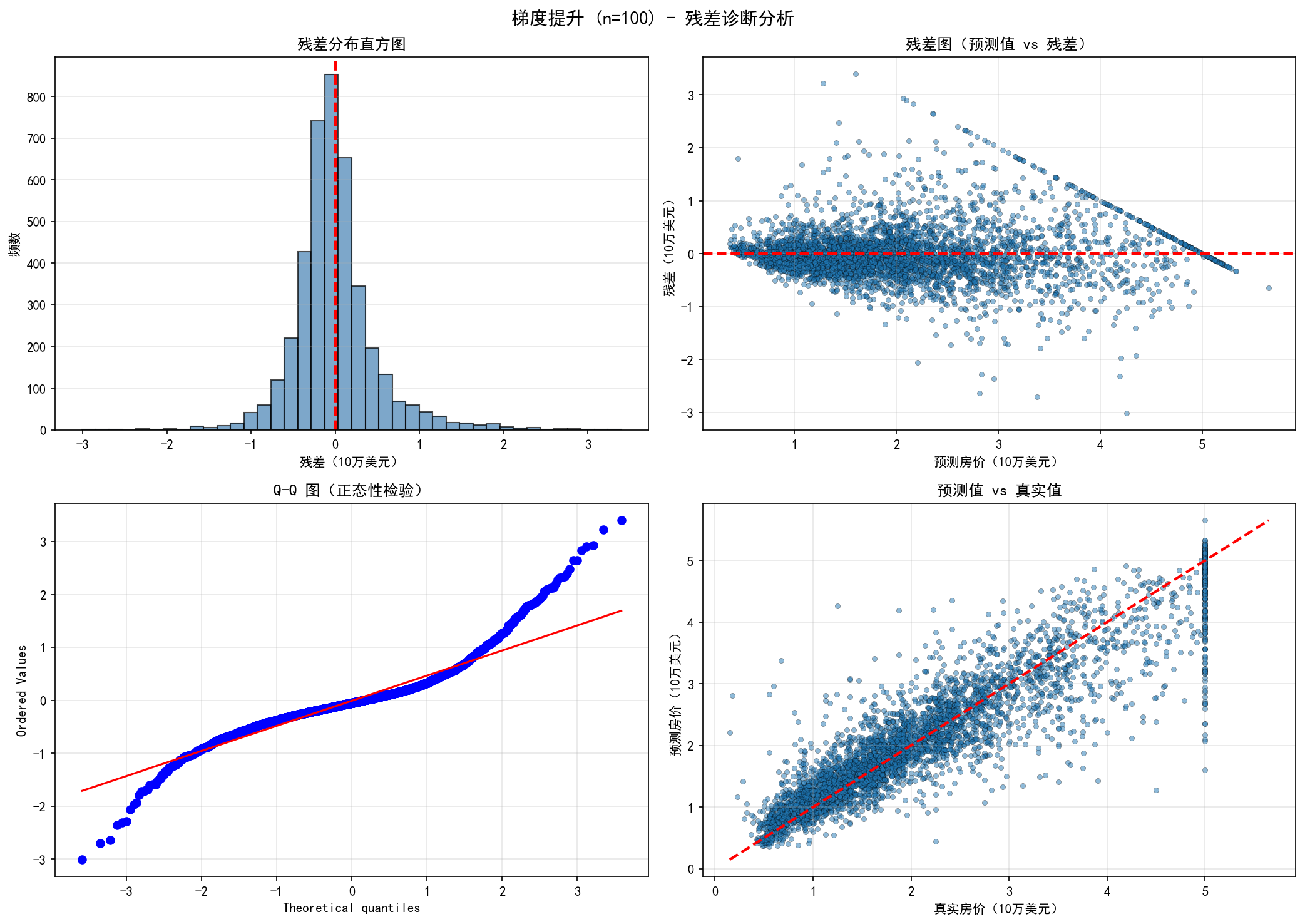
# 绘制残差诊断图
fig, axes = plt.subplots(2, 2, figsize=(14, 10))
fig.suptitle(f'{best_model_name} - 残差诊断分析', fontsize=14, fontweight='bold')
# 1. 残差分布直方图
axes[0, 0].hist(residuals, bins=40, edgecolor='black', alpha=0.7, color='steelblue')
axes[0, 0].set_xlabel('残差(10万美元)')
axes[0, 0].set_ylabel('频数')
axes[0, 0].set_title('残差分布直方图', fontweight='bold')
axes[0, 0].axvline(x=0, color='r', linestyle='--', linewidth=2)
axes[0, 0].grid(True, alpha=0.3, axis='y')
# 2. 预测值 vs 残差
axes[0, 1].scatter(best_predictions_test, residuals, alpha=0.5, s=15, edgecolors='k', linewidth=0.3)
axes[0, 1].axhline(y=0, color='r', linestyle='--', linewidth=2)
axes[0, 1].set_xlabel('预测房价(10万美元)')
axes[0, 1].set_ylabel('残差(10万美元)')
axes[0, 1].set_title('残差图(预测值 vs 残差)', fontweight='bold')
axes[0, 1].grid(True, alpha=0.3)
# 3. Q-Q 图
from scipy import stats
stats.probplot(residuals, dist="norm", plot=axes[1, 0])
axes[1, 0].set_title('Q-Q 图(正态性检验)', fontweight='bold')
axes[1, 0].grid(True, alpha=0.3)
# 4. 真实值 vs 预测值散点图
axes[1, 1].scatter(y_test, best_predictions_test, alpha=0.5, s=15, edgecolors='k', linewidth=0.3)
axes[1, 1].plot([min_val, max_val], [min_val, max_val], 'r--', linewidth=2)
axes[1, 1].set_xlabel('真实房价(10万美元)')
axes[1, 1].set_ylabel('预测房价(10万美元)')
axes[1, 1].set_title('预测值 vs 真实值', fontweight='bold')
axes[1, 1].grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('residual_analysis.png', dpi=150, bbox_inches='tight')
print("\n已保存: residual_analysis.png")
plt.close()
print("\n" + "="*100)
print("项目完成!所有结果已保存")
print("="*100)5.2 交叉验证与模型稳定性评估
上面的代码提供了完整的模型训练和评估。现在我们继续进行交叉验证评估,这能给出更稳定的性能估计。下面是一个完整的交叉验证代码,与上面的代码配合使用:
# 继续上面的代码,进行交叉验证评估
print("\n" + "="*100)
print("5折交叉验证深度评估")
print("="*100)
# 选择表现最好的几个模型进行交叉验证
cv_models = [
('线性回归', LinearRegression(), 'scaled'),
('Ridge回归 (α=1.0)', Ridge(alpha=1.0), 'scaled'),
('随机森林 (n=100)', RandomForestRegressor(n_estimators=100, max_depth=20, n_jobs=-1, random_state=42), 'original'),
('梯度提升 (n=100)', GradientBoostingRegressor(n_estimators=100, max_depth=5, learning_rate=0.1, random_state=42), 'original'),
]
X_full = X.values
y_full = y.values
X_full_scaled = scaler.fit_transform(X)
kfold = KFold(n_splits=5, shuffle=True, random_state=42)
cv_results = {}
for model_name, model, data_type in cv_models:
print(f"\n正在评估 {model_name}...", end=' ')
r2_scores = []
mae_scores = []
rmse_scores = []
mape_scores = []
fold_idx = 1
for train_idx, test_idx in kfold.split(X_full):
if data_type == 'scaled':
X_train_fold = X_full_scaled[train_idx]
X_test_fold = X_full_scaled[test_idx]
else:
X_train_fold = X_full[train_idx]
X_test_fold = X_full[test_idx]
y_train_fold = y_full[train_idx]
y_test_fold = y_full[test_idx]
model.fit(X_train_fold, y_train_fold)
y_pred_fold = model.predict(X_test_fold)
r2 = r2_score(y_test_fold, y_pred_fold)
mae = mean_absolute_error(y_test_fold, y_pred_fold)
rmse = np.sqrt(mean_squared_error(y_test_fold, y_pred_fold))
mape = np.mean(np.abs((y_test_fold - y_pred_fold) / y_test_fold)) * 100
r2_scores.append(r2)
mae_scores.append(mae)
rmse_scores.append(rmse)
mape_scores.append(mape)
fold_idx += 1
cv_results[model_name] = {
'R² Mean': np.mean(r2_scores),
'R² Std': np.std(r2_scores),
'R² Scores': np.array(r2_scores),
'MAE Mean': np.mean(mae_scores),
'MAE Std': np.std(mae_scores),
'MAE Scores': np.array(mae_scores),
'RMSE Mean': np.mean(rmse_scores),
'RMSE Std': np.std(rmse_scores),
'RMSE Scores': np.array(rmse_scores),
'MAPE Mean': np.mean(mape_scores),
'MAPE Std': np.std(mape_scores)
}
print(f"完成")
# 打印交叉验证结果
print("\n" + "="*120)
print("交叉验证结果汇总(5折)")
print("="*120)
cv_summary = []
for model_name in cv_results.keys():
results = cv_results[model_name]
cv_summary.append({
'模型': model_name,
'R² (Mean±Std)': f"{results['R² Mean']:.4f}±{results['R² Std']:.4f}",
'MAE (Mean±Std)': f"{results['MAE Mean']:.4f}±{results['MAE Std']:.4f}",
'RMSE (Mean±Std)': f"{results['RMSE Mean']:.4f}±{results['RMSE Std']:.4f}",
'MAPE (Mean±Std)': f"{results['MAPE Mean']:.2f}%±{results['MAPE Std']:.2f}%"
})
cv_summary_df = pd.DataFrame(cv_summary)
print(cv_summary_df.to_string(index=False))
print("="*120)
# 绘制交叉验证结果
fig, axes = plt.subplots(2, 2, figsize=(14, 10))
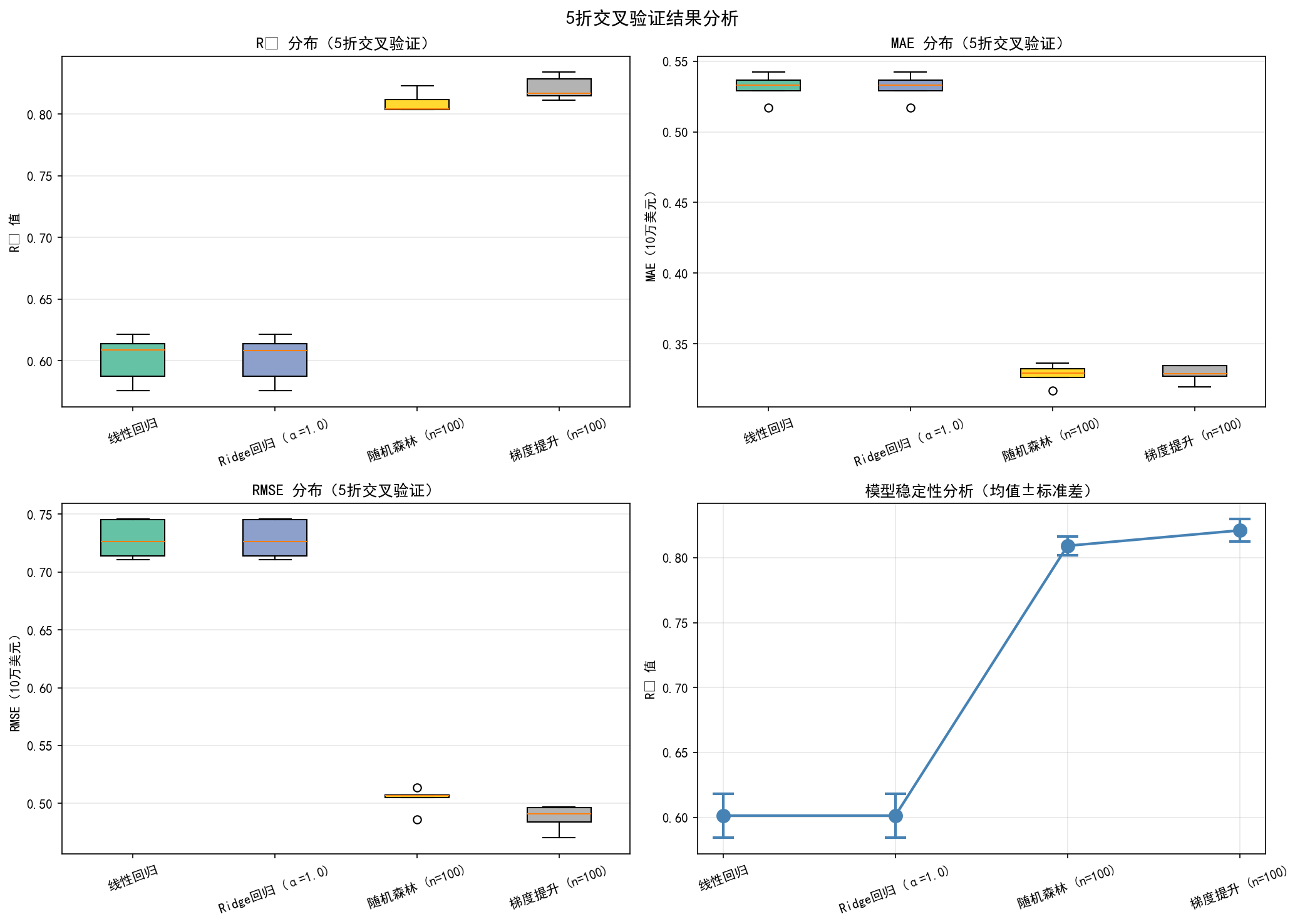
fig.suptitle('5折交叉验证结果分析', fontsize=14, fontweight='bold')
cv_model_names = list(cv_results.keys())
colors_cv = plt.cm.Set2(np.linspace(0, 1, len(cv_model_names)))
# 1. R² 箱线图
r2_data = [cv_results[m]['R² Scores'] for m in cv_model_names]
bp1 = axes[0, 0].boxplot(r2_data, labels=cv_model_names, patch_artist=True)
for patch, color in zip(bp1['boxes'], colors_cv):
patch.set_facecolor(color)
axes[0, 0].set_ylabel('R² 值')
axes[0, 0].set_title('R² 分布(5折交叉验证)', fontweight='bold')
axes[0, 0].tick_params(axis='x', rotation=20)
axes[0, 0].grid(True, alpha=0.3, axis='y')
# 2. MAE 箱线图
mae_data = [cv_results[m]['MAE Scores'] for m in cv_model_names]
bp2 = axes[0, 1].boxplot(mae_data, labels=cv_model_names, patch_artist=True)
for patch, color in zip(bp2['boxes'], colors_cv):
patch.set_facecolor(color)
axes[0, 1].set_ylabel('MAE(10万美元)')
axes[0, 1].set_title('MAE 分布(5折交叉验证)', fontweight='bold')
axes[0, 1].tick_params(axis='x', rotation=20)
axes[0, 1].grid(True, alpha=0.3, axis='y')
# 3. RMSE 箱线图
rmse_data = [cv_results[m]['RMSE Scores'] for m in cv_model_names]
bp3 = axes[1, 0].boxplot(rmse_data, labels=cv_model_names, patch_artist=True)
for patch, color in zip(bp3['boxes'], colors_cv):
patch.set_facecolor(color)
axes[1, 0].set_ylabel('RMSE(10万美元)')
axes[1, 0].set_title('RMSE 分布(5折交叉验证)', fontweight='bold')
axes[1, 0].tick_params(axis='x', rotation=20)
axes[1, 0].grid(True, alpha=0.3, axis='y')
# 4. 模型稳定性分析(均值±标准差)
r2_means = np.array([cv_results[m]['R² Mean'] for m in cv_model_names])
r2_stds = np.array([cv_results[m]['R² Std'] for m in cv_model_names])
x_pos = np.arange(len(cv_model_names))
axes[1, 1].errorbar(x_pos, r2_means, yerr=r2_stds, fmt='o-',
markersize=10, capsize=8, capthick=2, linewidth=2, color='steelblue')
axes[1, 1].set_xticks(x_pos)
axes[1, 1].set_xticklabels(cv_model_names, rotation=20)
axes[1, 1].set_ylabel('R² 值')
axes[1, 1].set_title('模型稳定性分析(均值±标准差)', fontweight='bold')
axes[1, 1].grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('cv_analysis.png', dpi=150, bbox_inches='tight')
print("\n已保存: cv_analysis.png")
plt.close()
# 打印模型排名
print("\n" + "="*100)
print("交叉验证模型排名(按R²均值从高到低)")
print("="*100)
cv_rankings = sorted(cv_results.items(), key=lambda x: x[1]['R² Mean'], reverse=True)
for rank, (model_name, results) in enumerate(cv_rankings, 1):
print(f"{rank}. {model_name:30s} | R² Mean: {results['R² Mean']:.4f}±{results['R² Std']:.4f} | "
f"RMSE Mean: ${results['RMSE Mean']*100000:8.2f}±${results['RMSE Std']*100000:6.2f}")
print("="*100)完整日志为:
====================================================================================================
California Housing 数据集加载与分析
====================================================================================================
数据集形状: (20640, 8)
样本数: 20640, 特征数: 8
目标变量(房价,单位:10万美元)统计:
均值: $206855.82
标准差: $115395.62
范围: [$14999.00, $500001.00]
已保存: housing_data_exploration.png
特征与房价的相关系数:
MedInc : 0.6881
AveRooms : 0.1519
HouseAge : 0.1056
AveOccup : -0.0237
Population : -0.0246
Longitude : -0.0460
AveBedrms : -0.0467
Latitude : -0.1442
已保存: housing_correlation_heatmap.png
数据分割:
训练集: 16512 样本
测试集: 4128 样本
====================================================================================================
模型训练与评估
====================================================================================================
正在训练: 线性回归... 完成 (Test R²: 0.5758)
正在训练: Ridge回归 (α=1.0)... 完成 (Test R²: 0.5758)
正在训练: Lasso回归 (α=0.01)... 完成 (Test R²: 0.5816)
正在训练: ElasticNet (α=0.01)... 完成 (Test R²: 0.5803)
正在训练: 决策树 (depth=20)... 完成 (Test R²: 0.6268)
正在训练: 随机森林 (n=100)... 完成 (Test R²: 0.8047)
正在训练: 梯度提升 (n=100)... 完成 (Test R²: 0.8110)
正在训练: AdaBoost (n=100)... 完成 (Test R²: 0.5311)
正在训练: SVR (RBF)... 完成 (Test R²: 0.7557)
正在训练: 神经网络... 完成 (Test R²: 0.7995)
============================================================================================================================================
模型评估结果总表
============================================================================================================================================
Train R² Test R² Test MAE Test RMSE Test MAPE 过拟合
线性回归 0.6126 0.5758 0.5332 0.7456 31.95% 0.0368
Ridge回归 (α=1.0) 0.6126 0.5758 0.5332 0.7456 31.95% 0.0367
Lasso回归 (α=0.01) 0.6085 0.5816 0.5353 0.7404 32.01% 0.0269
ElasticNet (α=0.01) 0.6101 0.5803 0.5341 0.7416 31.94% 0.0298
决策树 (depth=20) 0.9957 0.6268 0.4494 0.6994 24.58% 0.3690
随机森林 (n=100) 0.9721 0.8047 0.3279 0.5058 18.96% 0.1674
梯度提升 (n=100) 0.8695 0.8110 0.3349 0.4976 19.60% 0.0585
AdaBoost (n=100) 0.5479 0.5311 0.6498 0.7839 47.88% 0.0168
SVR (RBF) 0.8029 0.7557 0.3717 0.5658 20.45% 0.0472
神经网络 0.8378 0.7995 0.3467 0.5126 19.94% 0.0383
============================================================================================================================================
模型排名(按测试集R²从高到低)
============================================================================================================================================
1. 梯度提升 (n=100) | Test R²: 0.8110 | Test RMSE: $49764.50 | Test MAE: $33486.17 | 过拟合: 0.0585
2. 随机森林 (n=100) | Test R²: 0.8047 | Test RMSE: $50583.28 | Test MAE: $32793.02 | 过拟合: 0.1674
3. 神经网络 | Test R²: 0.7995 | Test RMSE: $51259.04 | Test MAE: $34667.15 | 过拟合: 0.0383
4. SVR (RBF) | Test R²: 0.7557 | Test RMSE: $56577.69 | Test MAE: $37170.25 | 过拟合: 0.0472
5. 决策树 (depth=20) | Test R²: 0.6268 | Test RMSE: $69935.62 | Test MAE: $44942.61 | 过拟合: 0.3690
6. Lasso回归 (α=0.01) | Test R²: 0.5816 | Test RMSE: $74044.24 | Test MAE: $53532.61 | 过拟合: 0.0269
7. ElasticNet (α=0.01) | Test R²: 0.5803 | Test RMSE: $74158.84 | Test MAE: $53407.72 | 过拟合: 0.0298
8. Ridge回归 (α=1.0) | Test R²: 0.5758 | Test RMSE: $74555.67 | Test MAE: $53319.31 | 过拟合: 0.0367
9. 线性回归 | Test R²: 0.5758 | Test RMSE: $74558.14 | Test MAE: $53320.01 | 过拟合: 0.0368
10. AdaBoost (n=100) | Test R²: 0.5311 | Test RMSE: $78388.68 | Test MAE: $64978.80 | 过拟合: 0.0168
============================================================================================================================================
已保存: housing_model_comparison.png
====================================================================================================
最佳模型详细分析: 梯度提升 (n=100)
====================================================================================================
模型性能指标:
训练集 R²: 0.869483
测试集 R²: 0.811013
测试集 MAE: 0.334862 (平均误差: $33486.17)
测试集 RMSE: 0.497645 (均方根误差: $49764.50)
测试集 MAPE: 19.60%
最大误差: $339885.90
过拟合程度: 0.058471
残差分析:
残差均值: -0.008179 (理想值为0)
残差标准差: 0.497578
残差范围: [-3.007558, 3.398859]
预测精度分析:
误差在 ±$33486.17 范围内的样本: 66.04%
误差在 ±$66972.33 范围内的样本: 87.74%
误差在 ±$100458.50 范围内的样本: 94.43%
已保存: residual_analysis.png
====================================================================================================
项目完成!所有结果已保存
====================================================================================================
====================================================================================================
5折交叉验证深度评估
====================================================================================================
正在评估 线性回归... 完成
正在评估 Ridge回归 (α=1.0)... 完成
正在评估 随机森林 (n=100)... 完成
正在评估 梯度提升 (n=100)... 完成
========================================================================================================================
交叉验证结果汇总(5折)
========================================================================================================================
模型 R² (Mean±Std) MAE (Mean±Std) RMSE (Mean±Std) MAPE (Mean±Std)
线性回归 0.6014±0.0170 0.5317±0.0084 0.7283±0.0149 31.76%±0.28%
Ridge回归 (α=1.0) 0.6014±0.0170 0.5317±0.0084 0.7282±0.0149 31.76%±0.28%
随机森林 (n=100) 0.8093±0.0074 0.3282±0.0066 0.5038±0.0094 18.47%±0.37%
梯度提升 (n=100) 0.8211±0.0086 0.3290±0.0055 0.4878±0.0099 18.80%±0.41%
========================================================================================================================
已保存: cv_analysis.png
====================================================================================================
交叉验证模型排名(按R²均值从高到低)
====================================================================================================
1. 梯度提升 (n=100) | R² Mean: 0.8211±0.0086 | RMSE Mean: $48775.73±$985.48
2. 随机森林 (n=100) | R² Mean: 0.8093±0.0074 | RMSE Mean: $50376.48±$936.28
3. Ridge回归 (α=1.0) | R² Mean: 0.6014±0.0170 | RMSE Mean: $72824.59±$1492.94
4. 线性回归 | R² Mean: 0.6014±0.0170 | RMSE Mean: $72825.09±$1493.55
====================================================================================================6. 指标选择与应用的实践指南
通过房价预测的完整项目,我们可以总结出几个重要的观察和结论。首先,不同类型的模型有不同的特点:线性模型虽然简单易懂,但对复杂非线性关系的拟合能力有限;树模型能够捕捉更复杂的特征交互,通常有更好的预测性能;神经网络模型具有很高的表达能力,但需要更多的调参和更大的计算资源。通过实验结果可以看到,梯度提升(Gradient Boosting)和随机森林(Random Forest)通常表现得最好,这与工业界的实践经验一致。
其次,过拟合是模型选择的重要考量。通过比较训练集和测试集的R²,我们可以识别出哪些模型在训练集上表现好但在测试集上表现下降的情况。例如,决策树通常具有较高的训练集R²但明显的过拟合现象。通过调节模型复杂度(如树的深度、正则化参数等)和使用交叉验证,可以有效地控制过拟合。在项目中,我们设置决策树的max_depth=20来控制其复杂度,这是一个很好的实践。
第三,评估指标的选择应该与业务目标相匹配。在房价预测中,MAE给出了平均预测误差的直观理解(每个预测平均错误多少钱),这对于房产中介或购房者来说是最有意义的指标。RMSE强调了大的预测错误,因为它使用平方运算,这在某些情况下更有用,例如当大的预测误差带来显著的成本增加时。R²说明了模型对房价变化的解释程度,反映了模型的整体拟合优度。在实际项目中,我们报告了所有三个指标,使得不同的利益相关者都能理解模型的性能。例如,技术人员关注R²和RMSE,而业务人员则关注MAE所代表的美元金额。
第四,交叉验证提供了更稳定和可靠的性能估计。项目中使用的5折交叉验证通过多次划分和平均,给出了每个模型性能的均值和标准差。标准差越小说明模型的性能越稳定。单一的train-test分割可能由于数据分割方式的不同而产生较大的波动,而交叉验证可以有效地消除这种随机性。通过观察cv_analysis.png中的箱线图,我们可以看到每个模型在不同折上的性能波动情况,这对于判断模型的可靠性非常重要。
第五,在实际应用中需要考虑的因素远不止指标数值。虽然梯度提升在我们的实验中表现最好,但在实际部署中,我们还需要考虑模型的计算效率、可维护性、可解释性等因素。例如,线性回归虽然R²相对较低,但其计算速度快、模型简单易理解,可能在某些场景下更适合部署。随机森林提供了特征重要性的信息,这对于理解房价的驱动因素很有帮助。这些非指标因素在真实的商业应用中往往同样重要,甚至有时更重要。
7. 总结与最佳实践
在机器学习的回归问题中,模型评估是一个至关重要的环节。通过本文详细的理论讲解和实际项目的完整演示,我们可以得出以下几个重要的结论和最佳实践建议。
关于评估指标的选择,应该根据具体的业务场景和数据特性来决定。MAE最适合当关注平均预测误差大小且数据包含离群点时的情况;RMSE最适合当关注预测偏差的波动性和极端情况时的情况;R²最适合需要衡量模型的整体拟合优度并进行不同规模数据之间的模型对比时的情况。在大多数情况下,同时报告MAE、RMSE和R²能够给出最全面的模型性能图景。通过房价项目的例子,我们看到了这三个指标如何互补地展现了模型的性能:MAE告诉购房者平均会错误多少美元,RMSE告诉我们预测的典型偏差有多大,R²告诉我们模型能解释房价变化的多少百分比。
关于模型选择和比较,应该使用多个指标、多个数据集分割方式和交叉验证来进行全面的评估。简单地看单一指标(如R²)容易导致误导的结论。应该观察训练集和测试集指标的差异来评估过拟合程度,在项目中我们通过"Overfitting Gap"这一指标量化了这种差异。应该观察指标在不同折的变化来评估模型的稳定性,通过交叉验证的均值和标准差我们能判断出梯度提升比线性回归更加稳定。对于包含离群点的数据,应该同时报告含异常值和不含异常值的结果,这在房价数据中尤其重要,因为极端豪宅会显著影响指标值。
关于指标的解释和应用,需要理解各个指标的数学意义和实际含义。MAE=0.5表示模型的平均预测误差为0.5个目标变量单位,在房价项目中这意味着平均每套房子的预测价格错误50万元;RMSE=0.6表示模型预测的均方根误差为0.6,这意味着存在一些较大的预测错误,其标准差为6万元;R²=0.85表示模型能解释目标变量变异的85%,这是一个相对较好的水平。评估指标的"好"还是"差"没有绝对标准,需要考虑问题的复杂度、数据的噪声水平、业务对精度的要求等多个因素。在房价预测中,R²=0.58的线性回归可能不够好,但R²=0.77的梯度提升就足够可用了。
关于实际应用中的常见陷阱,需要特别注意数据泄露。在项目中我们确保了特征标准化只使用训练集计算的参数应用到测试集,这是避免数据泄露的关键。需要避免的另一个陷阱是过度调参,过度的参数调优容易导致对特定数据集的过拟合。应该使用合理的验证策略,如我们项目中使用的5折交叉验证,来获得可靠的性能估计。还需要注意的是,高的R²或低的RMSE不一定意味着模型是好的,需要考虑模型的可解释性、计算成本、维护难度等多个因素。在房价预测项目中,尽管神经网络可能能达到更高的R²,但梯度提升可能是更好的选择,因为它更容易理解和维护。
关于最佳实践流程,推荐按照以下步骤进行:首先,进行探索性数据分析,理解特征的分布和与目标变量的关系,识别潜在的离群点和数据问题。在项目中我们通过直方图、热力图等方式理解了每个特征的性质。其次,采用合理的数据分割策略,将数据分为训练集和测试集,使用交叉验证来评估性能。再次,训练多个不同类型的模型,从简单到复杂逐步尝试。在项目中我们尝试了从线性回归到神经网络的十种不同模型。然后,在验证集或交叉验证的结果上选择超参数和最终模型。最后,在完全独立的测试集上进行最终评估,使用多个指标来全面评估模型性能,就像我们在项目中同时报告R²、MAE、RMSE等指标。
关于指标报告,应该遵循以下规范:明确说明使用的数据集(训练集还是测试集、是否包含异常值等),明确说明模型的具体配置(超参数值、特征选择方法等),说明指标的计算方法(如果有改进或变体的话),以及指标值的解释(这个R²值意味着什么)。对于重要的预测系统,应该定期监测指标,因为模型在生产环境中的性能可能随着数据分布的变化而下降。例如,如果房市发生重大变化,我们的模型可能需要重新训练。
总的来说,学会正确地理解和应用回归模型的评估指标,是成为一个专业的机器学习工程师或数据科学家的基础。这不仅帮助我们选择更好的模型,更重要的是帮助我们理解模型的优缺点,在实际应用中做出更明智的决策。通过本文的详细讲解和完整的房价预测项目案例,你已经掌握了如何在实际项目中系统地应用这些评估方法。希望你能在今后的工作中更加自信和高效地应用这些评估指标,推动机器学习项目的成功实施。