基于 Python 使用 SVM、K-means与DBSCAN

文章目录

- 一、支持向量机（SVM）
- - [1.1 SVM的核心参数与实现](#1.1 SVM的核心参数与实现)
  - [1.2 数据预处理与模型评估](#1.2 数据预处理与模型评估)
  - [1.3 模型训练与评估](#1.3 模型训练与评估)
- 二、K-means聚类算法
- - [2.1 聚类数量确定（轮廓系数法）](#2.1 聚类数量确定（轮廓系数法）)
  - [2.2 最佳K值可视化](#2.2 最佳K值可视化)
  - [2.3 最终聚类实现](#2.3 最终聚类实现)
- 三、DBSCAN密度聚类算法
- - [3.1 数据准备与预处理](#3.1 数据准备与预处理)
  - [3.2 DBSCAN核心参数与实现](#3.2 DBSCAN核心参数与实现)
  - [3.3 聚类结果分析](#3.3 聚类结果分析)

一、支持向量机（SVM）

支持向量机是一种强大的监督学习算法，主要用于分类问题。其核心思想是寻找一个最优超平面，使得不同类别之间的间隔最大化。

1.1 SVM的核心参数与实现

在Scikit-learn中，我们使用SVC类实现支持向量机分类。以下是关键参数分析：

python 复制代码

svm = SVC(kernel="linear", C=best_C, random_state=42)

参数解析：

kernel="linear"：指定使用线性核函数，适用于线性可分数据
C=best_C：正则化参数，控制分类错误的惩罚程度
- C值越小，决策边界越平滑，可能欠拟合
- C值越大，决策边界越复杂，可能过拟合
random_state=42：设置随机种子，确保结果可复现

1.2 数据预处理与模型评估

python 复制代码

# 数据标准化处理
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X_whole)

# 划分训练测试集（分层抽样）
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled, y_whole, test_size=0.3, random_state=42, stratify=y_whole
)

# 交叉验证寻找最优参数
C_values = [0.001, 0.01, 0.1, 1, 10]
for C in C_values:
    svm = SVC(kernel="linear", C=C, random_state=42)
    scores = cross_val_score(svm, X_train, y_train, cv=5, scoring='accuracy')

关键方法：

StandardScaler()：标准化处理，使特征均值为0，方差为1
stratify=y_whole：保持各类别在训练测试集中的比例一致
cross_val_score：5折交叉验证评估模型泛化能力

1.3 模型训练与评估

python 复制代码

# 使用最优参数训练模型
svm.fit(X_train, y_train)

# 预测与评估
train_pred = svm.predict(X_train)
test_pred = svm.predict(X_test)

print("训练集分类报告:")
print(metrics.classification_report(y_train, train_pred))
print("测试集分类报告:")
print(metrics.classification_report(y_test, test_pred))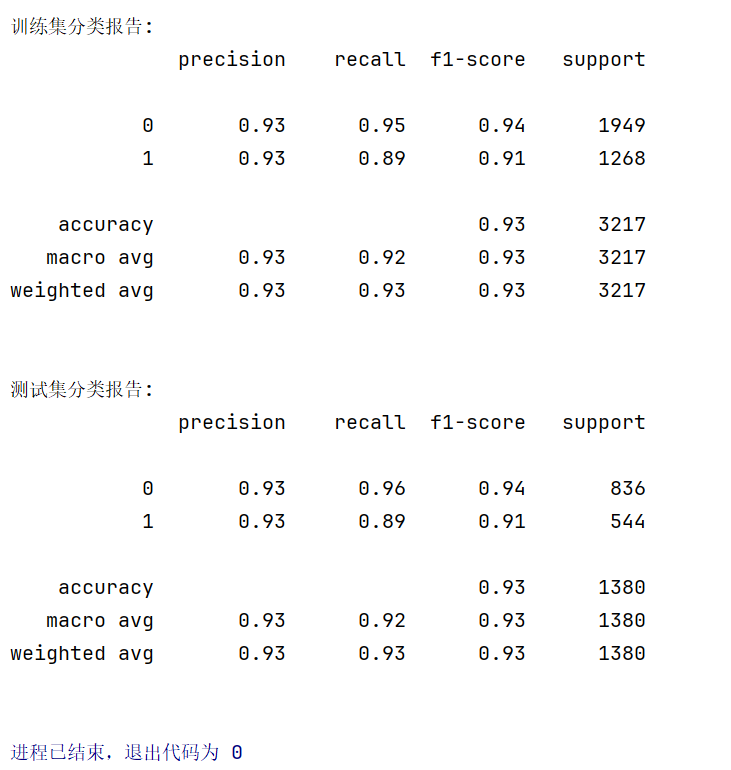

二、K-means聚类算法

K-means是一种经典的无监督聚类算法，通过迭代将数据划分为K个簇，使得每个数据点到其所属簇中心的距离最小。

2.1 聚类数量确定（轮廓系数法）

python 复制代码

scores = []
for k in range(2, 10):
    labels = KMeans(n_clusters=k).fit(X).labels_
    score = metrics.silhouette_score(X, labels)
    scores.append(score)

方法解析：

KMeans(n_clusters=k)：创建K-means模型，指定聚类数为k
silhouette_score：计算轮廓系数，评估聚类质量
- 值越接近1，表示聚类效果越好
- 值越接近-1，表示聚类效果越差

2.2 最佳K值可视化

python 复制代码

plt.plot(list(range(2, 10)), scores)
plt.xlabel("Number of Clusters Initialized")
plt.ylabel("Silhouette Score")
plt.show()

2.3 最终聚类实现

python 复制代码

km = KMeans(n_clusters=3).fit(X)
y = km.labels_
score = metrics.silhouette_score(X, y)
print(score)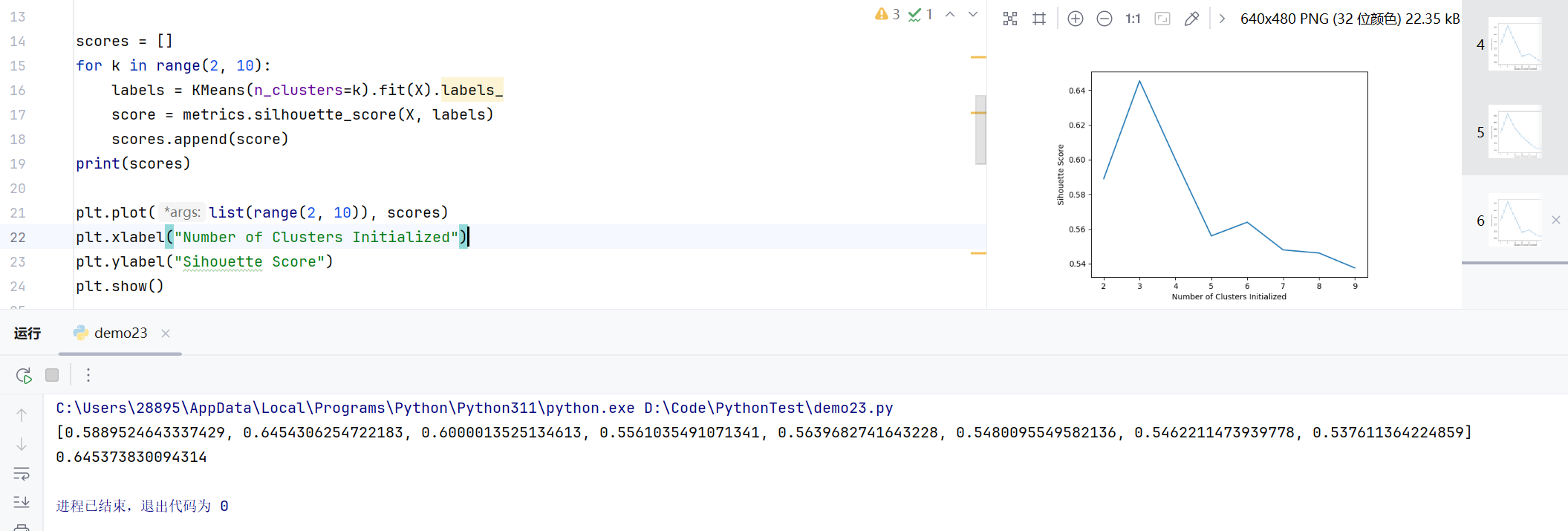

三、DBSCAN密度聚类算法

DBSCAN是一种基于密度的聚类算法，能够识别任意形状的簇，并自动检测噪声点。

3.1 数据准备与预处理

python 复制代码

# 数据加载与特征选择
a = np.loadtxt(r"datingTestSet2.txt", delimiter='\t')
data = pd.DataFrame(a)
X = data.iloc[:, 0: 3]
y = data.iloc[:, -1]

# DBSCAN对特征尺度敏感，必须进行标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

3.2 DBSCAN核心参数与实现

python 复制代码

db = DBSCAN(eps=0.5, min_samples=5).fit(X_scaled)
labels = db.labels_

参数解析：

eps=0.5：邻域半径，决定数据点的邻域范围
- 值过大：将更多点纳入同一簇，可能合并本应分开的簇
- 值过小：大多数点被标记为噪声，难以形成有效簇
min_samples=5：形成核心点的最小样本数
- 值越大：对核心点要求更严格，更多点被标记为噪声
- 值越小：更容易形成核心点，但可能产生过多小簇

3.3 聚类结果分析

python 复制代码

# 计算聚类数量和噪声点
n_clusters = len(set(labels)) - (1 if -1 in labels else 0)
n_noise = list(labels).count(-1)

print(f"聚类数量（不含噪声）: {n_clusters}")
print(f"噪声点数量: {n_noise}")
print(f"噪声点比例: {n_noise / len(labels):.2%}")