第2讲:模型选择与评估 ------ 深度复习笔记
一、 核心理论:VC维与可学习性 (Computational Theory)
这部分通常考察选择题或简答题,核心是理解模型复杂度与样本量的关系。
- 基本定义 :
- 泛化误差 (EoutE_{out}Eout) vs 经验误差 (EinE_{in}Ein) :训练时的误差是 EinE_{in}Ein,我们真正关心的是在未来未知数据上的 EoutE_{out}Eout。目标是 Eout≈Ein≈0E_{out} \approx E_{in} \approx 0Eout≈Ein≈0。
- 散列 (Shattering) :如果假设空间 HHH 能把数据集 DDD 中的 mmm 个样本的所有 2m2^m2m 种对分形式(即所有可能的正负标记组合)都表示出来,称 HHH 能散列 DDD。
- VC维 (dVCd_{VC}dVC) :假设空间 HHH 能散列 的最大 数据集的大小。
- 举例:二维平面上线性分类器(直线)的 VC 维是 3(它可以散列3个点,但不能散列4个点,比如XOR分布),。
- 一般结论:ddd 维空间的线性超平面的 VC 维是 d+1d+1d+1。
- VC维的物理意义(考试重点) :
- VC维反映了模型的复杂度 或学习能力。
- 泛化界 :EoutE_{out}Eout 和 EinE_{in}Ein 的差值被 VC 维约束。P[∣Eout−Ein∣>ϵ]≤4(2m)dVCexp(...)P[|E_{out} - E_{in}| > \epsilon] \le 4(2m)^{d_{VC}} \exp(...)P[∣Eout−Ein∣>ϵ]≤4(2m)dVCexp(...)。
- 结论 :模型越复杂(dVCd_{VC}dVC 越大),EinE_{in}Ein 容易很小,但泛化界变宽,容易过拟合。
- 样本量需求 :理论上需要 m≈10,000⋅dVCm \approx 10,000 \cdot d_{VC}m≈10,000⋅dVC,实际工程中经验法则是 m≈10⋅dVCm \approx 10 \cdot d_{VC}m≈10⋅dVC。
二、 误差分析:偏差-方差分解 (Bias-Variance Decomposition)

这段图片展示的是机器学习中非常核心的一个概念:偏差-方差分解 (Bias-Variance Decomposition) 。
简单来说,当我们评价一个模型的表现时,我们不仅关心它在某一次训练上的好坏,更关心它在不同数据集上的稳健性 。这四个公式通过数学方式,把模型预测产生的误差拆解成了三个部分:偏差、方差和噪声 。
为了让你看清楚这些值是怎么算的,我们先明确几个符号的含义:
- xxx:一个具体的测试样本。
- yyy:该样本对应的真实值(理想状态下,没有任何误差的值)。
- yDy_DyD:在训练集 DDD 中观察到的标签值 (可能带有噪声,即 yD=y+ϵy_D = y + \epsilonyD=y+ϵ)。
- y^D\hat{y}_Dy^D:使用数据集 DDD 训练出来的模型对 xxx 做出的预测值。
- ED[... ]\mathbb{E}_D[\dots]ED[...]:表示在多个不同的训练集 DDD 上取数学期望(你可以理解为多次实验的平均值)。
1. 期望输出 (Expected Prediction)
ED[y^D]\mathbb{E}_D[\hat{y}_D]ED[y^D]
- 怎么算: 想象你从总体中随机抽取 100 个不同的训练集,每个训练集都练出一个模型。对于同一个输入 xxx,这 100 个模型会给你 100 个预测结果。把这 100 个结果加起来除以 100,得到的就是"平均预测值"。
- 意义: 它代表了学习算法本身的平均拟合能力。
2. 方差 (Variance)
ED[(y^D−ED[y^D])2]\mathbb{E}_D[(\hat{y}_D - \mathbb{E}_D[\hat{y}_D])^2]ED[(y^D−ED[y^D])2]
- 怎么算: 先算出上面的"平均预测值",然后计算每一个具体的预测值 y^D\hat{y}_Dy^D 与平均值之间的偏离程度。
- 意义: 衡量的是数据的扰动对模型的影响 。如果方差很大,说明换一个训练集,模型的预测结果就会剧烈变化。这通常意味着模型过拟合 (Overfitting) 了,它对训练集的细节(甚至噪声)太敏感。
3. 噪声 (Noise)
ϵ2=ED[(yD−y)2]\epsilon^2 = \mathbb{E}_D[(y_D - y)^2]ϵ2=ED[(yD−y)2]
- 怎么算: 这是训练集里的标签值 yDy_DyD 与客观真值 yyy 之间的差异。
- 意义: 这是不可消除的最小误差。它由数据采集过程中的随机性、测量误差等决定。无论你的模型多完美,这部分误差永远存在(泛化误差的下界)。
4. 偏差平方 (Bias²)
bias2=(ED[y^D]−y)2bias^2 = (\mathbb{E}_D[\hat{y}_D] - y)^2bias2=(ED[y^D]−y)2
- 怎么算: 用模型的"平均预测值"减去"客观真值",再平方。
- 意义: 衡量模型偏离真实情况的程度 。如果偏差很高,说明模型本身的假设就不对,无法捕捉数据的基本规律。这通常意味着模型欠拟合 (Underfitting)
总结:打靶类比
为了直观理解,我们可以把模型预测比作打靶:
- 低偏差,低方差:所有子弹都紧紧地落在靶心周围(最理想)。
- 低偏差,高方差:子弹分布在靶心周围,但非常分散(过拟合)。
- 高偏差,低方差:子弹扎堆在一起,但全偏离了靶心(欠拟合,模型学错了方向)。
- 高偏差,高方差 :子弹既分散,又离靶心远(最差的情况)。
最终结论:
一个模型的总误差(泛化误差)可以分解为:
Total Error=Bias2+Variance+Noise\text{Total Error} = \text{Bias}^2 + \text{Variance} + \text{Noise}Total Error=Bias2+Variance+Noise
你要做的就是通过调整模型的复杂度(比如正则化、改变神经元数量等),在偏差和方差之间找到一个平衡点。
这部分极易出分析题 或计算题,必须背诵公式和结论。
- 公式分解 : 泛化误差可以分解为三部分,: E=bias2+variance+noiseE = bias^2 + variance + noiseE=bias2+variance+noise
- 偏差 (Bias) :期望预测值 fˉ(x)\bar{f}(x)fˉ(x) 与真实值 yyy 的差距。反映算法的拟合能力(准不准)。
- 方差 (Variance) :不同训练集导致的预测值 f(x;D)f(x;D)f(x;D) 的变化幅度。反映算法的稳定性(稳不稳)。
- 噪声 (Noise):数据本身的质量问题,是学习性能的上限(不可约减误差)。
- "鱼和熊掌不可兼得" (Trade-off) :
- 欠拟合 (Underfitting) :模型太简单 →\rightarrow→ 高偏差,低方差。
- 过拟合 (Overfitting) :模型太复杂 →\rightarrow→ 低偏差,高方差。
- 图形记忆:随着训练程度/模型复杂度增加,偏差曲线下降,方差曲线上升,总误差曲线呈现 U 型。
- K近邻 (KNN) 的特例 ,:
- 小 k 值 (如 1-NN):模型复杂(边界破碎),低偏差,高方差(容易过拟合)。
- 大 k 值 :模型简单(边界平滑),高偏差,低方差(容易欠拟合)。
三、 模型评估方法 (Validation Methods)
考试通常考察在特定数据集规模下,应该选择哪种方法。
- 留出法 (Hold-out) :
- 直接将 DDD 分为互斥的训练集 SSS 和测试集 TTT(如 7/3 分)。
- 关键点 :必须保持数据分布一致性(分层采样 Stratified Sampling)。
- 缺点:受划分方式影响大,需要多次随机划分求平均。
- k折交叉验证 (k-fold Cross Validation) :
- 将 DDD 分为 kkk 个互斥子集。每次用 k−1k-1k−1 个训练,1个测试,轮转 kkk 次。
- 留一法 (LOO) :k=mk=mk=m(样本数)。优点是评估准确(不受随机划分影响),缺点是计算量极大。
- 自助法 (Bootstrapping) ,:
- 做法 :有放回采样 mmm 次。
- 包外估计 (Out-of-bag) :约 36.8% 的样本未出现在训练集中 (limm→∞(1−1/m)m≈1/e≈0.368\lim_{m\to\infty}(1-1/m)^m \approx 1/e \approx 0.368limm→∞(1−1/m)m≈1/e≈0.368),用作测试集。
- 适用场景:数据集较小,或难以有效划分训练/测试集时。
- 缺点:改变了初始数据集的分布,会引入估计偏差。
四、 性能度量指标 (Performance Metrics)
这是计算题的高频考点,务必记准公式
- 混淆矩阵 (Confusion Matrix) :
- TP (真两性), FN (假阴性/漏报), FP (假阳性/误报), TN (真阴性)。
- 核心指标 :
- 查准率 (Precision) :P=TPTP+FPP = \frac{TP}{TP + FP}P=TP+FPTP (预测出的正例里,多少是真的?)
- 查全率 (Recall) :R=TPTP+FNR = \frac{TP}{TP + FN}R=TP+FNTP (所有真值正例里,找出了多少?)
- F1 Score :F1=2×P×RP+RF1 = \frac{2 \times P \times R}{P + R}F1=P+R2×P×R (P和R的调和平均,用于平衡两者)。
- 曲线与面积 :
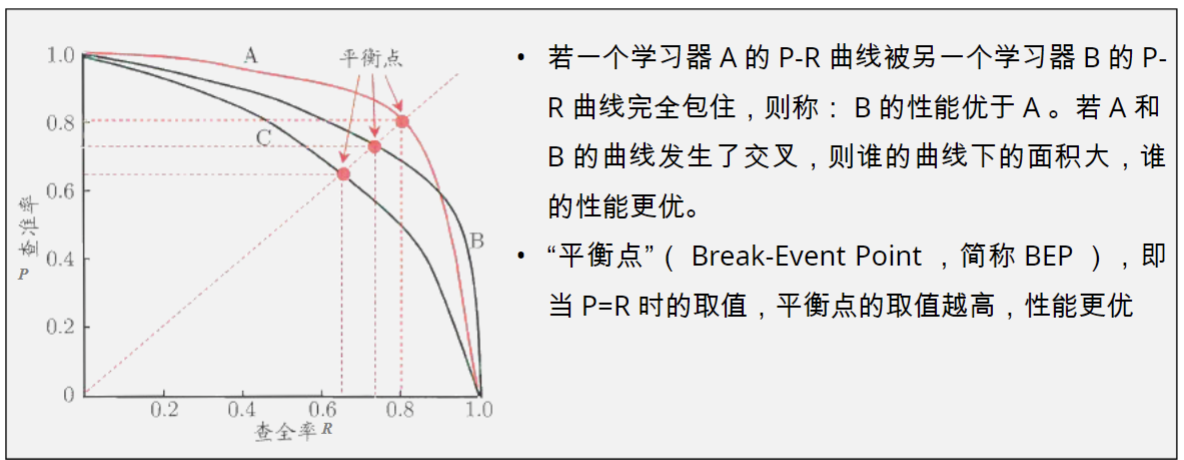
- P-R 曲线 :横轴 Recall,纵轴 Precision。平衡点 (BEP) 是 P=RP=RP=R 时的取值。曲线完全包住另一个则更优。
- ROC 曲线 :
- 横轴:FPR (假正例率) =FPTN+FP= \frac{FP}{TN + FP}=TN+FPFP (1 - 特异性)
- 纵轴:TPR (真正例率) =TPTP+FN= \frac{TP}{TP + FN}=TP+FNTP (Recall, 灵敏度)
- AUC :ROC 曲线下的面积。AUC 越大,分类器排序能力越强,泛化性能越好。
- 做题技巧 :如果给出几个点的预测概率和真实标签,要会手画 ROC 曲线并计算 AUC(通过梯形面积法)。

之所以这些比率(TPR, FPR, Precision 等)会发生变化,是因为在将"概率"转化成"分类标签"时,我们人为设置了一个**"门槛"------分类阈值 (Threshold)**。
1. 核心原因:从"概率"到"标签"
绝大多数分类模型(比如逻辑回归、神经网络)输出的不是直接的 000 或 111,而是一个 000 到 111 之间的概率值 (例如:0.850.850.85 可能是正类的概率)。
为了得到最终结果,你需要画一条线:
- 默认情况下 :如果你觉得概率 >0.5> 0.5>0.5 就是正类,那么 0.60.60.6 的样本被分为"正"。
- 严格情况下 :如果你把门槛提到 0.90.90.9,那么这个 0.60.60.6 的样本就会被重新划分为"负"。
模型没变,但因为你的"门槛"变了,预测出来的标签分布就变了,从而导致各种比率跟着动。
2. 想象一个"滑动条"
ROC 和 PR 曲线其实就是记录了阈值从 0 逐渐移动到 1 的全过程:
- 当阈值设为 0 :模型把所有东西都预测为"正"。
- 结果:你抓住了所有坏人(Recall=1),但也冤枉了所有好人(FPR=1)。
- 当阈值设为 1 :模型把所有东西都预测为"负"。
- 结果:你一个好人也没冤枉(FPR=0),但也一个坏人也没抓到(Recall=0)。
- 在 0 到 1 之间滑动 :你会得到无数个 (TPR, FPR) 点。把这些点连起来,就成了 ROC 曲线。
3. 为什么要变这个阈值?
因为在现实生活中,犯错的代价是不一样的:
- 场景 A:癌症筛查(宁可错杀一千,不可放过一个)
你会调低阈值。即使只有 0.20.20.2 的概率是癌症,也要标记为正。这时你的 Recall (召回率) 很高,但 Precision (精确率) 会下降,因为误报多了。 - 场景 B:垃圾邮件过滤(宁可漏掉垃圾邮件,不可误删重要邮件)
你会调高阈值。只有 0.990.990.99 确定是垃圾邮件才拦截。这时你的 Precision 很高,但 Recall 会下降,因为很多垃圾邮件漏掉了。
总结
- 模型输出的概率 是定死的。
- 曲线 展示的是:当我们作为决策者,在**"激进"和"保守"**之间反复横跳(改变阈值)时,模型的整体抗压能力。
- AUC(面积) 的意义就在于:它不看某一个具体的阈值,而是衡量在所有可能的阈值下,模型的综合表现好不好。
五、 模型比较检验 (Hypothesis Testing)
这部分通常考概念,或者是判断"模型A比模型B好"是否具有统计学意义。
- 目的:判断两个模型的性能差异不是由随机性引起的。
- McNemar 检验 :
- 用于二分类问题。
- 关注两个模型预测结果不一致 的情况(即 e01e_{01}e01:A对B错,e10e_{10}e10:A错B对)。
- 统计量 τχ2=(∣e01−e10∣−1)2e01+e10\tau_{\chi^2} = \frac{(|e_{01} - e_{10}| - 1)^2}{e_{01} + e_{10}}τχ2=e01+e10(∣e01−e10∣−1)2 服从自由度为 1 的卡方分布,。
这两张图片是关于机器学习模型评估中非常重要的统计检验(Hypothesis Testing)方法。
简单来说,之前的 ROC/PR 曲线是衡量模型"好不好"的指标 ,而这两张图教你如何通过数学手段判断这个"好"是确有其事 ,还是只是运气好碰上的随机误差。
第一张图:单模型泛化错误率检验 (ttt 检验)
这张图的核心目的是:判断一个模型的泛化错误率是否等于我们预设的目标值 ϵ0\epsilon_0ϵ0。
- 背景: 你训练了一个模型,测了 kkk 次(比如用了 kkk 折交叉验证),得到了 kkk 个不同的错误率 ϵ^1,...,ϵ^k\hat{\epsilon}_1, \dots, \hat{\epsilon}_kϵ^1,...,ϵ^k。
- 计算过程:
- 计算这 kkk 个错误率的平均值 μ\muμ 和 方差 σ2\sigma^2σ2。
- 提出假设: * H0H_0H0(原假设):模型的平均错误率就是 ϵ0\epsilon_0ϵ0。
- H1H_1H1(备择假设):模型的平均错误率不等于 ϵ0\epsilon_0ϵ0。
- 构造统计量 τt\tau_tτt: 利用公式计算出一个 ttt 值。这个值符合自由度为 k−1k-1k−1 的 ttt 分布。
- 如何看结果(右侧的图):
- 中间白色的区域是"接受域",两侧阴影部分是"拒绝域"
- 如果计算出来的 τt\tau_tτt 掉进了阴影区(显著性水平 α\alphaα 之外),我们就认为:模型表现和预期 ϵ0\epsilon_0ϵ0 之间有显著差异,原来的假设不对。
第二张图:两模型边际同质性检验 (McNemar 检验)
这张图的核心目的是:比较两个分类模型(模型 A 和模型 B)到底谁更好,还是说它们其实半斤八两。
- 背景: 仅仅看准确率(Accuracy)是不够的。我们需要对比两个模型在同一个测试集上的具体表现差异。
- 列联表(中间的表格): 这是理解的关键。
- e00e_{00}e00:两个模型都预测正确。
- e11e_{11}e11:两个模型都预测错误。
- e01e_{01}e01 和 e10e_{10}e10(重点): 这是两个模型"产生分歧"的地方。e01e_{01}e01 表示 B 对 A 错,e10e_{10}e10 表示 A 对 B 错。
- 核心逻辑:
- 如果模型 A 和 B 的性能真的没区别,那么按理说:A 赢 B 的次数 (e10e_{10}e10) 应该等于 B 赢 A 的次数 (e01e_{01}e01)。
- 计算统计量 τχ2\tau_{\chi^2}τχ2:
- 公式为 τχ2=(∣e01−e10∣−1)2e01+e10\tau_{\chi^2} = \frac{(|e_{01} - e_{10}| - 1)^2}{e_{01} + e_{10}}τχ2=e01+e10(∣e01−e10∣−1)2。
- 这个公式符合 卡方 (χ2\chi^2χ2) 分布。
- 结论: * 如果算出来的 τχ2\tau_{\chi^2}τχ2 很大,说明 e01e_{01}e01 和 e10e_{10}e10 差得太远了。
- 这意味着:两个模型之间存在显著的性能差异。
总结:这两张图在工程中有什么用?
- 避开"虚假繁荣": 有时候模型 A 比模型 B 准确率高了 1%1\%1%,但这可能是因为测试集太小导致的随机波动。
- 科学评估: * 如果你想证明你的改进是有意义的,你需要做 McNemar 检验 。
- 如果你想证明你的模型达到了交付标准(错误率低于某值),你需要做 ttt 检验。
小贴士: McNemar 检验在实际论文和大型算法竞赛中非常常用,因为它不需要像交叉验证那样跑很多次模型,只需要对比两组预测结果的差异即可。