算法基础（数论）—费马小定理

费⻢⼩定理

【同余式】
• 如果两个整数 a , b 模 m 的余数相同，则称 a , b 模 m 同余，记作： a ≡ b (mod m ) 。
例如： 7 ≡ 4 (mod 3)

---

性质
• 同加性：若 a ≡ b (mod m ) ，则 a + c ≡ b + c (mod m )
• 同乘性：若 a ≡ b (mod m ) ，则 ac ≡ bc (mod m )
也就是说，对于同余的两个数，执⾏完相同的加减乘操作后，它们两者还是同余的。
• 但是同余不满⾜同除性，例如 20 ≡ 2(mod 3) ，左右都除以 10 ，结果就不是同余的。

---

这就解释了为什么之前遇到需要取模的题⽬，如果只涉及加减乘运算，我们可以边计算边取模。⽽存 在除法的时候，不能随意取模。

---

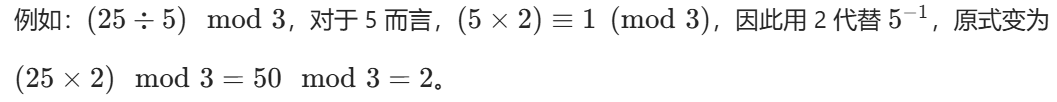
代码实现：

#include <iostream>
using namespace std;
typedef long long LL;
// 必须要保证 a,p 互质，且 p 为质数。
LL qpow(LL a, LL b, LL p)
{
LL ret = 1;
while(b)
{
if(b & 1) ret = ret * a % p;
b >>= 1;
a = a * a % p;
}
return ret;
}
int main()
{
LL x, p; cin >> n >> p;
cout << qpow(x, p - 2, p) << endl;
return 0;
}

---

时间复杂度：
• 与快速幂时间复杂度⼀致，为 O (log n ) 。

---

1 ⽔上舞者索尼娅

题⽬来源： 洛⾕
题⽬链接： P11465 ⽔上舞者索尼娅
难度系数： ★★

题目背景

2024 年 12 月 18 日，《炉石传说》31.2.2 补丁上线，水上舞者索尼娅遭到削弱。现在，在这道题目中，你打开时空之门，回到了水索被削弱前的时候。

题目描述

你的场上有 k 个【水上舞者索尼娅】，你的手牌中有 1 张法力值消耗为 1 的【一串香蕉（还剩 n 根）】，你有无尽的法力值，你的手牌数量没有上限。

在你的场上有 k 个【水上舞者索尼娅】的情况下：

当你使用 1 张法力值消耗为 1 的【一串香蕉（还剩 x 根）】时，你将得到：

• k 张法力值消耗为 0 的【一串香蕉（还剩 x 根）】。
• 1 张法力值消耗为 1 的【一串香蕉（还剩 x−1 根）】。（若 x=1，则不会得到）

当你使用 1 张法力值消耗为 0 的【一串香蕉（还剩 x 根）】时，你将得到：

• 1 张法力值消耗为 1 的【一串香蕉（还剩 x−1 根）】。（若 x=1，则不会得到）

你一共可以使用多少次【一串香蕉】？

由于答案可能很大，你只需求出答案对 109+7 取模的余数。

输入格式

本题有多组数据。

第一行一个正整数 T，表示数据组数。

对于每组数据：

一行两个正整数 n,k。

输出格式

对于每组数据：

输出一行一个整数，表示答案对 109+7 取模的余数。

输入输出样例

输入 #1复制

3
2 2
3 1
12 34

输出 #1复制

12
14
178629506

说明/提示

1≤T≤105， 1≤n,k≤109。

【样例解释】

对于第 1 组数据：

场上有 2 个【水上舞者索尼娅】，初始手牌中有 1 张法力值消耗为 1 的【一串香蕉（还剩 2 根）】。

使用：1 张法力值消耗为 1 的【一串香蕉（还剩 2 根）】。

手牌：

• 2 张法力值消耗为 0 的【一串香蕉（还剩 2 根）】。
• 1 张法力值消耗为 1 的【一串香蕉（还剩 1 根）】。

使用：2 张法力值消耗为 0 的【一串香蕉（还剩 2 根）】。

手牌：

• 3 张法力值消耗为 1 的【一串香蕉（还剩 1 根）】。

使用：3 张法力值消耗为 1 的【一串香蕉（还剩 1 根）】。

手牌：

• 6 张法力值消耗为 0 的【一串香蕉（还剩 1 根）】。

使用：6 张法力值消耗为 0 的【一串香蕉（还剩 1 根）】。

手牌：

• 空

共使用 1+2+3+6=12 张【一串香蕉】。

---

【解法】

等⽐数列求和公式。

---

【参考代码】

#include <iostream>
using namespace std;

typedef long long LL;
const int MOD = 1e9 + 7;  // 把p改成MOD，更易读

// 快速幂：计算 (a^b) % mod
LL quick_pow(LL a, LL b, LL mod) {
    LL result = 1;
    a = a % mod;  // 先取模，防止a太大
    while (b > 0) {
        // b是奇数，结果乘a
        if (b & 1) {
            result = (result * a) % mod;
        }
        // b除以2，a平方
        b >>= 1;
        a = (a * a) % mod;
    }
    return result;
}

int main() {
    ios::sync_with_stdio(false);  // 加速输入输出（可选，汇报时可以说）
    cin.tie(nullptr);
    
    int T;
    cin >> T;
    while (T--) {
        LL n, k;
        cin >> n >> k;
        
        // 计算 (k+1)^(n+1) mod MOD
        LL pow_val = quick_pow(k + 1, n + 1, MOD);
        // 计算 (pow_val - (k+1)) mod MOD
        LL numerator = (pow_val - (k + 1)) % MOD;
        // 计算k的逆元：k^(MOD-2) mod MOD
        LL inv_k = quick_pow(k, MOD - 2, MOD);
        // 计算最终结果：分子 × 逆元 mod MOD
        LL ans = (numerator * inv_k) % MOD;
        
        // 确保结果非负
        ans = (ans + MOD) % MOD;
        cout << ans << endl;
    }
    return 0;
}

2 序列求和

题⽬来源： 洛⾕
题⽬链接： 序列求和
难度系数： ★

---

链接：https://ac.nowcoder.com/acm/problem/15950

来源：牛客网

题号：NC15950

时间限制：C/C++/Rust/Pascal 1秒，其他语言2秒

空间限制：C/C++/Rust/Pascal 128 M，其他语言256 M

64bit IO Format: %lld

题目描述

定义S(n) = 12 + 22 + ... + n2，输出S(n) % 1000000007。

注意：1 < n < 1e18。

输入描述:

多组输入，输入直到遇到EOF为止；

第一行输入一个正整数n。

输出描述:

输出S(n) % 1000000007的结果。

示例1

输入

复制1 2 1000

1
2
1000

输出

复制1 5 333833500

1
5
333833500

---

【解法】

计算公式。
注意，因为 n 很⼤，随便乘⼀下就会变得很⼤，因此要先取模，然后再乘。

---

【参考代码】

#include <iostream>
using namespace std;

typedef long long LL;
const int MOD = 1e9 + 7;  // 把p改成MOD，更易读

// 快速幂：计算 (a^b) % mod，用于求乘法逆元
LL quick_pow(LL a, LL b, LL mod) {
    LL result = 1;
    a = a % mod;  // 先对a取模，防止a过大
    while (b > 0) {
        // b为奇数时，结果乘a并取模
        if (b & 1) {
            result = (result * a) % mod;
        }
        // b除以2，a平方后取模
        b >>= 1;
        a = (a * a) % mod;
    }
    return result;
}

int main() {
    // 加速输入输出（可选，汇报时可以提）
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    LL n;
    // 多组输入，直到EOF
    while (cin >> n) {
        // 分步计算公式中的每一项，先取模避免溢出
        LL term1 = n % MOD;                  // n mod MOD
        LL term2 = (n + 1) % MOD;            // (n+1) mod MOD
        LL term3 = (2 * n + 1) % MOD;        // (2n+1) mod MOD
        LL inv_6 = quick_pow(6, MOD - 2, MOD);  // 6的逆元
        
        // 分步相乘取模，保证每一步都不溢出
        LL ans = (term1 * term2) % MOD;
        ans = (ans * term3) % MOD;
        ans = (ans * inv_6) % MOD;
        
        cout << ans << endl;
    }
    return 0;
}

---

欧拉定理

---

1 【模板】扩展欧拉定理

题⽬来源： 洛⾕

题⽬链接： P5091 【模板】扩展欧拉定理

难度系数： ★★★★

题目背景

出题人也想写有趣的题面，可惜并没有能力。

题目描述

给你三个正整数，a,m,b，你需要求：abmodm

输入格式

一行三个整数，a,m,b

输出格式

一个整数表示答案

输入输出样例

输入 #1复制

2 7 4

输出 #1复制

2

输入 #2复制

998244353 12345 98765472103312450233333333333

输出 #2复制

5333

说明/提示

注意输入格式，a,m,b 依次代表的是底数、模数和次数

【样例 1 解释】

24mod7=2

【数据范围】

对于 100% 的数据，1≤a≤109，1≤b≤1020000000，1≤m≤108。

---

【解法】

模板题。

---

【参考代码】

#include <iostream>
#include <string>
using namespace std;
typedef long long LL;

// 试除法求单个x的欧拉函数φ(x)
LL get_phi(LL x) {
    LL ret = x;
    for (int i = 2; i <= x / i; ++i) {
        if (x % i == 0) {
            // 欧拉函数核心公式：ret = ret * (i-1)/i（先除后乘防溢出）
            ret = ret / i * (i - 1);
            // 去重：把x中所有i的因子删掉
            while (x % i == 0) {
                x /= i;
            }
        }
    }
    // 处理剩余的质因数
    if (x > 1) {
        ret = ret / x * (x - 1);
    }
    return ret;
}

// 处理超大指数b（字符串存储），按扩展欧拉定理降幂
LL get_b(string& s, LL phi) {
    LL t = 0;
    bool flag = false; // 标记b是否≥phi
    for (char ch : s) {
        t = t * 10 + (ch - '0');
        // 如果当前t≥phi，说明b≥phi，需要降幂
        if (t >= phi) {
            flag = true;
            t %= phi; // 取模缩小t
        }
    }
    // 扩展欧拉定理：b≥phi时，指数= t + phi
    if (flag) {
        t += phi;
    }
    return t;
}

// 快速幂：计算 (a^b) % p
LL qpow(LL a, LL b, LL p) {
    LL ret = 1;
    a = a % p; // 先对a取模，避免溢出
    while (b > 0) {
        // b为奇数时，结果乘a并取模
        if (b & 1) {
            ret = (ret * a) % p;
        }
        // b除以2，a平方后取模
        b >>= 1;
        a = (a * a) % p;
    }
    return ret;
}

int main() {
    // 加速输入输出
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    LL a, m;
    string s; // 用字符串存超大的指数b
    cin >> a >> m >> s;

    // 步骤1：求m的欧拉函数φ(m)
    LL phi = get_phi(m);
    // 步骤2：处理超大指数b，按扩展欧拉定理降幂
    LL b = get_b(s, phi);
    // 步骤3：快速幂计算a^b mod m
    LL ans = qpow(a, b, m);

    cout << ans << endl;
    return 0;
}

---

2 上帝与集合的正确⽤法

题⽬来源： 洛⾕
题⽬链接： P4139 上帝与集合的正确⽤法
难度系数： ★★★★
题目描述

根据一些书上的记载，上帝的一次失败的创世经历是这样的：

第一天，上帝创造了一个世界的基本元素，称做元。

第二天，上帝创造了一个新的元素，称作 α 。 α 被定义为元构成的集合。容易发现，一共有两种不同的 α 。

第三天，上帝又创造了一个新的元素，称作 β 。 β 被定义为 α 构成的集合。容易发现，一共有四种不同的 β。

第四天，上帝创造了新的元素 γ，γ 被定义为 β 的集合。显然，一共会有 16 种不同的 γ。

如果按照这样下去，上帝创造的第四种元素将会有 65536 种，第五种元素将会有 265536种。这将会是一个天文数字。

然而，上帝并没有预料到元素种类数的增长是如此的迅速。他想要让世界的元素丰富起来，因此，日复一日，年复一年，他重复地创造着新的元素......

然而不久，当上帝创造出最后一种元素 θ 时，他发现这世界的元素实在是太多了，以致于世界的容量不足，无法承受。因此在这一天，上帝毁灭了世界。

至今，上帝仍记得那次失败的创世经历，现在他想问问你，他最后一次创造的元素 θ 一共有多少种？

上帝觉得这个数字可能过于巨大而无法表示出来，因此你只需要回答这个数对 p 取模后的值即可。

你可以认为上帝从 α 到 θ 一共创造了 109 次元素，或 1018 次，或者干脆 ∞ 次。

一句话题意：

定义 a0​=1,an​=2an−1​，可以证明 bn​=an​modp 在某一项后都是同一个值，求这个值。

输入格式

第一行一个整数 T，表示数据个数。

接下来 T 行，每行一个正整数 p，代表你需要取模的值。

输出格式

T 行，每行一个正整数，为答案对 p 取模后的值。

输入输出样例

输入 #1复制

3
2
3
6

输出 #1复制

0
1
4

说明/提示

对于 100% 的数据，T≤103，p≤107。

---

【解法】

递归 + 欧拉降幂 + 打表欧拉函数 + 快速幂。

【参考代码】

#include <iostream>         // 输入输出头文件
using namespace std;
typedef long long LL;       // 把long long简写为LL，避免重复写
const int N = 1e7 + 10;     // 数组最大长度（10000010）
bool st[N];                 // 标记是否是合数（非质数）
int p[N], cnt;              // p[]存质数，cnt是质数的个数
int phi[N];                 // phi[i]存欧拉函数φ(i)

// 第一步：预处理所有数的欧拉函数（打表）
void get_phi() {
    int n = 1e7;
    phi[1] = 1;             // 1的欧拉函数是1（规定）
    for(int i = 2; i <= n; i++) {  // 从2开始算每个数的φ(i)
        if(!st[i]) {        // 如果i是质数（没被标记过）
            phi[i] = i - 1; // 质数的欧拉函数是它本身-1（比如3→2，5→4）
            p[++cnt] = i;   // 把质数存到p[]里，cnt加1
        }
        // 用已有的质数，算i×p[j]的欧拉函数（线性筛）
        for(int j = 1; 1ll * i * p[j] <= n; j++) {
            int x = i * p[j];  // x是i和质数p[j]的乘积
            st[x] = true;      // 标记x是合数
            if(i % p[j] == 0) { // 如果i能被p[j]整除（x是i的倍数，且p[j]是i的质因子）
                phi[x] = phi[i] * p[j]; // 欧拉函数公式：φ(i×p[j])=φ(i)×p[j]
                break;                // 退出循环，避免重复计算
            } else {            // 如果i和p[j]互质
                phi[x] = phi[i] * (p[j] - 1); // φ(i×p[j])=φ(i)×(p[j]-1)
            }
        }
    }
}

// 第二步：快速幂函数------计算 (a^b) mod p 的结果
LL qpow(LL a, LL b, LL p) {
    LL ret = 1;             // ret是结果，初始为1
    while(b) {              // 只要指数b不为0
        if(b & 1) {         // 如果b的二进制最后一位是1（b是奇数）
            ret = ret * a % p; // 结果乘a，再取模p
        }
        b >>= 1;            // b右移一位（相当于除以2）
        a = a * a % p;      // a平方，再取模p（指数拆半，底数平方）
    }
    return ret;             // 返回最终结果
}

// 第三步：递归计算最终的固定余数
int dfs(int p) {
    if(p == 1) return 0;    // 边界：p=1时，任何数mod1都是0
    // 核心：用欧拉降幂，计算2^(dfs(φ(p)) + φ(p)) mod p
    return qpow(2, dfs(phi[p]) + phi[p], p);
}

// 主函数：程序入口
int main() {
    get_phi();              // 先预处理所有欧拉函数（打表）
    int T; cin >> T;        // 输入测试用例个数T
    while(T--) {            // 循环T次，处理每个测试用例
        int p; cin >> p;    // 输入当前的p
        cout << dfs(p) << endl; // 计算并输出结果
    }
    return 0;               // 程序结束
}

---

裴蜀定理

【裴蜀定理】
裴蜀定理⼜称⻉祖定理：
• ⼀定存在整数 x , y ，满⾜ ax + by = gcd ( a , b ) 。
可以⽤来判定不定⽅程是否存在整数解。
例如 6 x + 8 y = gcd (6, 8) = 2 ，⼀定有整数解。
其中 x = −1, y = 1 就是⼀组解。

---

【裴蜀定理的推论】

1. ⼀定存在整数 x , y ，满⾜ ax + by = gcd ( a , b ) × n
   因此，对于⼀个⼆元⼀次不定⽅程 ax + by = c ，当 gcd ( a , b ) ∣ c 时，有解。
2. ⼀定存在整数 x 1 , x 2 , x 3 ... ，满⾜ a 1 x 1 + a 2 x 2 + a 3 x 3 + ... a k x k = gcd ( a 1 , a 2 , a 3 ... a k ) × n 。

---

【注意】
a b的正负是不影响结果的。因为a,b 如果存在解，那么a,-b 也⼀定存在解，只不过在 a,b解的
基础上添上⼀个负号。
因此，在⽤欧⼏⾥得算法求 gcd ( a , b ) 时，为了避免出现负数，可以带⼊ a , b 的绝对值。

---

1 【模板】裴蜀定理

题⽬来源： 洛⾕
题⽬链接： P4549 【模板】裴蜀定理
难度系数： ★★

题目描述

给定一个包含 n 个元素的整数序列 A，记作 A1​,A2​,A3​,...,An​。

求另一个包含 n 个元素的待定整数序列 X，记 S=i=1∑n​Ai​×Xi​，使得 S>0 且 S 尽可能的小。

输入格式

第一行一个整数 n，表示序列元素个数。

第二行 n 个整数，表示序列 A。

输出格式

一行一个整数，表示 S>0 的前提下 S 的最小值。

输入输出样例

输入 #1复制

2
4059 -1782

输出 #1复制

99

说明/提示

对于 100% 的数据，1≤n≤20，∣Ai​∣≤105，且 A 序列不全为 0。

---

【解法】

模板题，本质就是在求所有系数的最⼤公约数。

---

【参考代码】

#include <iostream>
using namespace std;
int gcd(int a, int b)
{
return b == 0 ? a : gcd(b, a % b);
}
int main()
{
int n; cin >> n;
int ret; cin >> ret; ret = abs(ret);
for(int i = 2; i <= n; i++)
{
int x; cin >> x;
ret = gcd(ret, abs(x));
}
cout << ret << endl;
return 0;
}

---

.扩展欧⼏⾥得算法

【扩展欧⼏⾥得算法】
裴蜀定理那⾥还遗留⼀个问题，如何求： ax + by = gcd ( a , b ) 的⼀组整数解？
利⽤扩展欧⼏⾥得算法就可以求解。

【代码实现】

LL exgcd(LL a, LL b, LL& x, LL& y)
{
if(b == 0)
{
x = 1, y = 0;
return a;
}
LL x1, y1, d;
// 先求出下⼀层的 x1 和 y1
d = exgcd(b, a % b, x1, y1);
// 求当前层
x = y1, y = x1 - a / b * y1;
return d;
}
int main()
{
int a, b, x, y;
int d = exgcd(a, b, x, y);
cout << x << " " << y << endl;
return 0;
}

时间复杂度：
与欧⼏⾥得算法得时间复杂度⼀致，为 O (log n ) 。

---

---

同余⽅程

【同余⽅程】
• 求同余⽅程 ax ≡ b (mod m ) 的解。
例如：求 4 x ≡ 2(mod 6) ，其中⼀个解为 x = 2

【扩欧算法求同余⽅程的解】
同余⽅程可以转换为⼆元⼀次不定⽅程：
• 由 ax ≡ b (mod m ) 可得： ax = ym + b ，移项得 ax − my = b ；
• 令 y = − y ，就变成⼆元⼀次不定⽅程： ax + my = b ；
• 由裴蜀定理得，当 gcd ( a , m ) ∣ b 时，有解。
那么，就可以⽤扩展欧⼏⾥得算法求出 x 的值。

---

【扩欧算法求乘法逆元】
• 特殊的，如果 b 等于 1 ，原⽅程变为 ax ≡ 1(mod m ) ，解出的 x 实际上就是 a 在模 m 意义
下的乘法逆元。
因此，利⽤扩欧算法也可以求出乘法逆元。并且不需要模数 m 是质数，仅需 gcd( a , m ) = 1 ，也就
是 a , m 互质即可。

---

1 【模板】同余⽅程

题⽬来源： ⽜客⽹
题⽬链接： 【模板】同余⽅程
难度系数： ★★★
链接： https://ac.nowcoder.com/acm/problem/229005
来源：牛客网

题号：NC229005

时间限制：C/C++/Rust/Pascal 1秒，其他语言2秒

空间限制：C/C++/Rust/Pascal 256 M，其他语言512 M

64bit IO Format: %lld

题目描述

求关于 x\ x x 的同余方程ax≡1(modb)a x \equiv 1\pmod {b}ax≡1(modb)的最小正整数解，若无解，输出"-1"。

输入描述:

第一行一个正整数 T\ T T，表示 T\ T T组数据。
接下来 T\ T T行，每行两个正整数 a,b(2≤a,b≤2∗109)\ a,b(2≤a,b≤2*10^9) a,b(2≤a,b≤2∗109)。

输出描述:

对于每组数据，输出同余方程的最小正整数解，若无解，输出"-1"（没有引号）。

示例1

输入

复制2 3 10 2 4

2
3 10
2 4

输出

复制7 -1

7
-1

---

【解法】模板题。

---

【参考代码】

#include <iostream>
using namespace std;
typedef long long LL;  // 定义LL代替long long，避免数字太大溢出（a/b最大2e9，普通int装不下）

// 扩展欧几里得函数：返回a和b的最大公约数d，同时通过引用修改x、y，使得a*x + b*y = d
LL exgcd(LL a, LL b, LL& x, LL& y)
{
    if(b == 0)  // 递归边界：b=0时，a就是最大公约数
    {
        x = 1, y = 0;  // 此时a*1 + 0*0 = a = d，满足a*x + b*y = d
        return a;      // 返回最大公约数d
    }
    // 递归：先求exgcd(b, a%b, x1, y1)，得到b*x1 + (a%b)*y1 = d
    LL x1, y1;
    LL d = exgcd(b, a % b, x1, y1);
    // 核心转换：把下一层的x1/y1转成当前层的x/y
    x = y1;
    y = x1 - a / b * y1;
    return d;  // 返回最大公约数d
}

int main()
{
    int T; cin >> T;  // 输入测试用例个数T
    while(T--)        // 循环处理每组数据
    {
        LL a, b; cin >> a >> b;  // 输入每组的a和b
        LL x, y, d;              // x/y存exgcd结果，d存最大公约数
        d = exgcd(a, b, x, y);   // 调用exgcd，得到d、x、y
        if(d == 1)  // 有解：a和b互质
        {
            // 把x调整为最小正整数：x%b可能是负数，加b再取模保证正
            x = (x % b + b) % b;
            cout << x << endl;   // 输出答案
        }
        else  // 无解
        {
            cout << -1 << endl;
        }
    }
    return 0;
}

---

2 ⻘蛙的约会

题⽬来源： 洛⾕
题⽬链接： P1516 ⻘蛙的约会
难度系数： ★★★

题目描述

两只青蛙在网上相识了，它们聊得很开心，于是觉得很有必要见一面。它们很高兴地发现它们住在同一条纬度线上，于是它们约定各自朝西跳，直到碰面为止。可是它们出发之前忘记了一件很重要的事情，既没有问清楚对方的特征，也没有约定见面的具体位置。不过青蛙们都是很乐观的，它们觉得只要一直朝着某个方向跳下去，总能碰到对方的。但是除非这两只青蛙在同一时间跳到同一点上，不然是永远都不可能碰面的。为了帮助这两只乐观的青蛙，你被要求写一个程序来判断这两只青蛙是否能够碰面，会在什么时候碰面。

我们把这两只青蛙分别叫做青蛙 A 和青蛙 B，并且规定纬度线上东经 0 度处为原点，由东往西为正方向，单位长度 1 米，这样我们就得到了一条首尾相接的数轴。设青蛙 A 的出发点坐标是 x，青蛙 B 的出发点坐标是 y。青蛙 A 一次能跳 m 米，青蛙 B 一次能跳 n 米，两只青蛙跳一次所花费的时间相同。纬度线总长 L 米。现在要你求出它们跳了几次以后才会碰面。

输入格式

输入只包括一行五个整数 x,y,m,n,L。

输出格式

输出碰面所需要的次数，如果永远不可能碰面则输出一行一个字符串 Impossible。

输入输出样例

输入 #1复制

1 2 3 4 5

输出 #1复制

4

说明/提示

对于 100% 的数据，1≤x,y,m,n≤2×109，x=y，1≤L≤2.1×109。

---

【解法】

⼩学数学题。
设：相遇时跳了 t 次，
• 由题意可得： x + tm − ( y + tn ) = lz ，其中 z 是整数。也就是 A ⻘蛙的路程 - B ⻘蛙的路程
移项合并后可得：

【参考代码】

#include <iostream>
using namespace std;

// 定义long long别名，避免数字太大溢出（题目中数值可能很大）
typedef long long LL;

/**
 * 扩展欧几里得算法（exgcd）
 * 功能：1. 求a和b的最大公约数d；2. 找到x、y满足 a*x + b*y = d
 * 参数：a,b - 输入的两个数；x,y - 引用类型，用于返回满足式子的解
 * 返回值：a和b的最大公约数d
 */
LL exgcd(LL a, LL b, LL& x, LL& y)
{
    // 递归边界：当b=0时，a就是最大公约数d
    if(b == 0)
    {
        x = 1;  // 此时a*1 + 0*0 = a = d，满足式子
        y = 0;
        return a; // 返回最大公约数
    }
    // 递归调用：先求exgcd(b, a%b, x1, y1)，得到b*x1 + (a%b)*y1 = d
    LL x1, y1, d;
    d = exgcd(b, a % b, x1, y1);
    // 核心转换：把下一层的x1/y1转化为当前层的x/y
    x = y1;
    y = x1 - a / b * y1;
    return d; // 返回最大公约数
}

int main()
{
    // 输入参数：x(A初始位置)、y(B初始位置)、m(A每次跳的距离)、n(B每次跳的距离)、l(纬度线总长)
    LL x, y, m, n, l;
    cin >> x >> y >> m >> n >> l;

    // 把青蛙相遇问题转化为扩展欧几里得的标准形式：a*t + b*z = c
    // 原相遇条件：x + m*t = y + n*t + z*l → (m-n)*t - l*z = y - x
    LL a = m - n;  // 系数t的部分
    LL b = l;      // 系数z的部分（对应原式子的-l）
    LL c = y - x;  // 等式右边的常数

    // 把a转为正数（方便计算，不影响最终结果）
    if(a < 0)
    {
        a = -a;
        c = -c;
    }

    LL x0, y0, d;
    // 调用exgcd：d是a和b的最大公约数，x0/y0是满足a*x0 + b*y0 = d的解
    d = exgcd(a, b, x0, y0);

    // 判断是否有解：只有c能被d整除时，才有满足条件的t
    if(c % d != 0)
    {
        cout << "Impossible" << endl;
    }
    else
    {
        // 把x0放大c/d倍，得到满足a*t + b*z = c的一个解t0
        x0 = c / d * x0;
        // 解的周期：找最小正整数解需要用到
        LL k1 = b / d;
        // 把x0调整为最小的正整数解（避免负数）
        LL ans = (x0 % k1 + k1) % k1;
        cout << ans << endl;
    }

    return 0;
}

---

. 逆元

【乘法逆元】
乘法逆元，⼀般⽤于求a/b(mod p ) 的值。
先算出b 在模p 意义下的乘法逆元 ，然后计算ax(mod)p 的值，就可以将除法转化为 乘法。

---

总结⼀下求逆元的各种⽅法。
【⽅法⼀：费⻢⼩定理 + 快速幂】
• 问题：求 a 在模 m 意义下的逆元。
• 前提条件： a , m 互质，且 m 是质数；
• ⽅法：求出 ，就是 a 在模 m 意义下的逆元。
• 时间复杂度： O (log m ) 。

---

// 必须要保证 a,m 互质，且 m 为质数。
LL qpow(LL a, LL b, LL m)
{
LL ret = 1;
while(b)
{
if(b & 1) ret = ret * a % m;
b >>= 1;
a = a * a % m;
}
return ret;
}
int main()
{
LL x, m; cin >> x >> m;
cout << qpow(x, m - 2, m) << endl;
return 0;
}

---

【⽅法⼆：扩欧算法求逆元】
• 问题：求 a 在模 m 意义下的逆元。
• 前提条件： a , m 互质；
• ⽅法：解同余⽅程 ax ≡ 1(mod m ) 。
• 时间复杂度： O (log m ) 。

LL exgcd(LL a, LL b, LL& x, LL& y)
{
if(b == 0)
{
x = 1, y = 0;
return a;
}
LL x1, y1, d;
d = exgcd(b, a % b, x1, y1);
x = y1, y = x1 - a / b * y1;
return d;
}
int main()
{
LL a, m; cin >> a >> m;
LL x, y, d;
d = exgcd(a, m, x, y);
if(d == 1) cout << (x % m + m) % m) << endl;
return 0;
}

---

【⽅法三：递推法】
• 问题：求 1 ∼ n 中所有的数在模 p 意义下的逆元。
• 前提条件： 1 ∼ n 中所有的数都与 p 互质。
• ⽅法：线性递推：
◦ 当 i = 1 ： inv [1] = 1
◦ 当 i > 1 ： inv [ i ] = p − ( p / i ) × inv [ p mod i ] mod p
• 时间复杂度： O ( m ) 。

代码块
LL n, p;
LL inv[N];
void get_inv()
{
inv[1] = 1;
for(int i = 2; i <= n; i++)
{
inv[i] = p - p / i * inv[p % i] % p;
}
}

---