【做题总结】顺子（双指针）

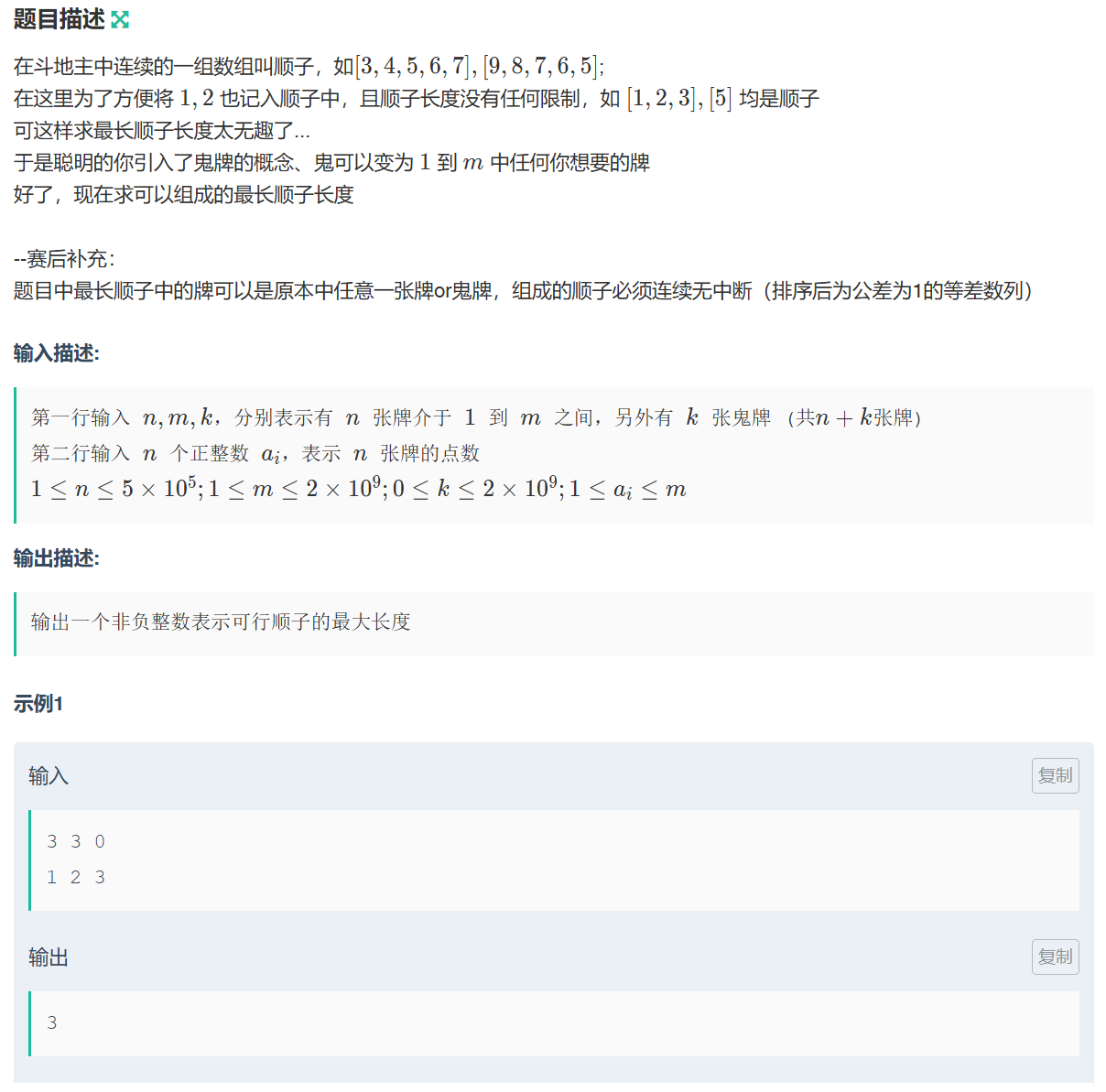
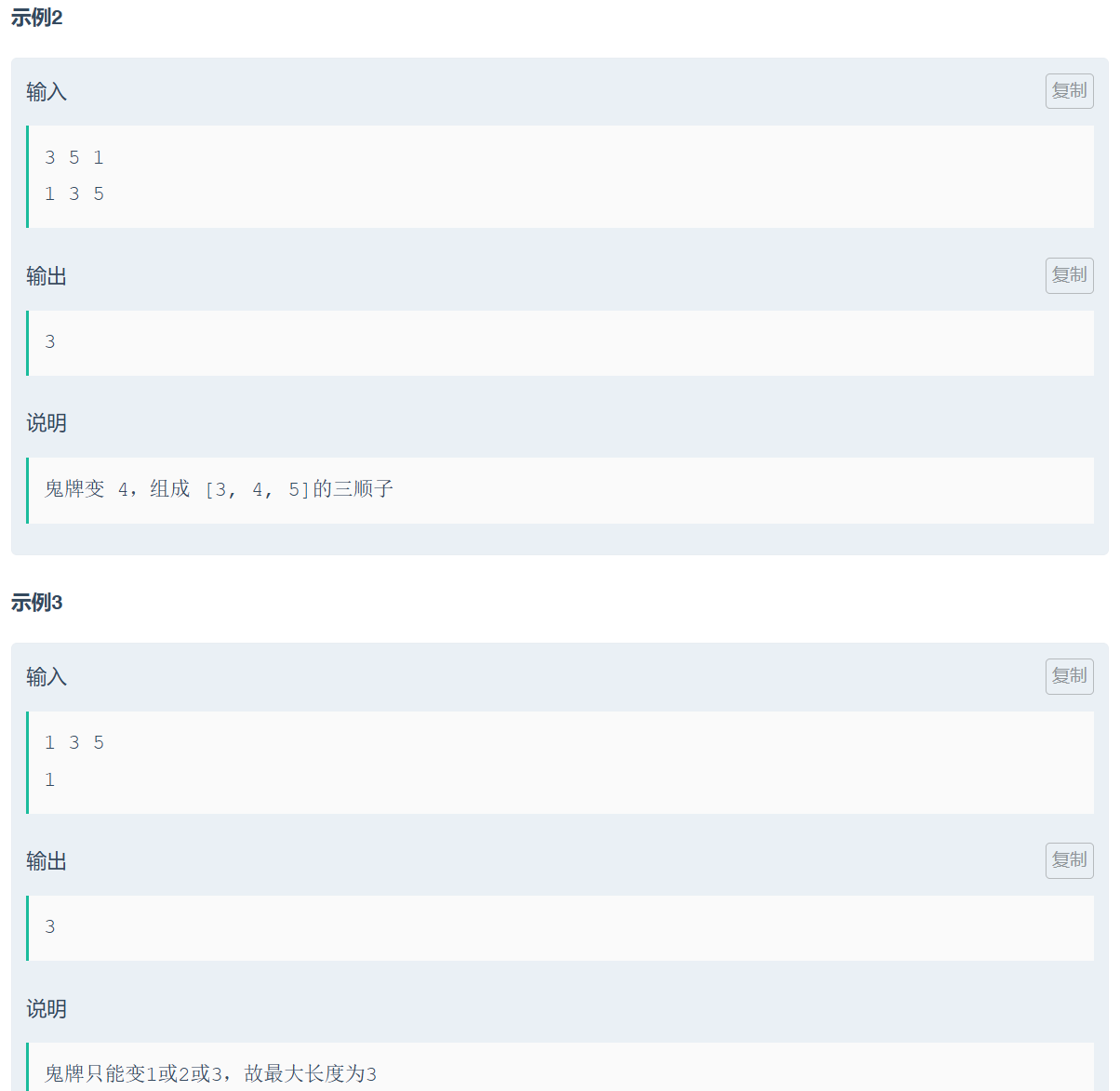
这道题考的细节挺多的：

1. 数据规模：m的范围到2×10^9，我原本想用前缀和统计1至m范围空缺的牌数，但这个规模数组是很难容纳的。
2. 输入的牌，可能有牌数重复的，所以要做去重和排序。
3. 我在写代码的时候，一直被边界问题困扰了比较久，以及程序的整体思路也不太清晰。这里理了一下思路：
   ①预处理：对输入数组排序并去重，去除重复牌以减少无效计算。
   ②双指针初始化：设置左指针 l=0，右指针 i 从 1 开始遍历去重后的数组；定义 c 统计 l,i 区间内需要的鬼牌数（空缺数）。
   ③空缺数计算：遍历过程中，累加 l,i 区间内相邻牌的空缺数（公式：ai-ai-1-1）到 c。
   ④窗口收缩：若 c > k（空缺数超过鬼牌数），则右移左指针 l，并减去移出区间对应的空缺数，直到 c ≤ k。
   ⑤答案更新：计算剩余鬼牌数 r = k - c；当前窗口补全空缺后的基础长度为 ai-al+1，剩余鬼牌可向区间两侧扩展，最终长度需满足不超过 m；用 ans = max(ans, min(m, ai-al+1 + r - (l == 0))) 更新答案。
   ** 减 (l==0) 是因为 a0 是虚拟哨兵值（非有效牌），当 l=0 时，基础长度公式会多算 1，需用⑥该修正项抵消误差。
   输出结果：遍历结束后，输出最大顺子长度 ans。

AC代码：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,m,k,a[500005],ans,c;
int main(){
	cin>>n>>m>>k;
	for(int i=1;i<=n;i++) cin>>a[i];
	sort(a+1,a+n+1);
	int p=unique(a+1,a+n+1)-(a+1);
	a[0]=0;
	ll l=0;
	for(ll i=1;i<=p;i++){
		if(i>l) c+=a[i]-a[i-1]-1;
		while(c>k&&l<i){
			l++;
			c-=a[l]-a[l-1]-1;
		}
		ll r=k-c;
		if(r>=0) ans=max(ans,min(m,a[i]-a[l]+1+r-(l==0)));
	}
	cout<<ans;
	return 0;
}