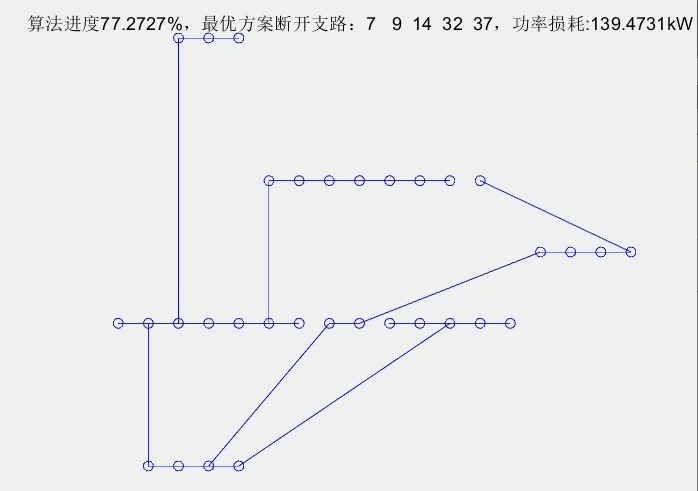
改进二进制粒子群算法配电网重构 可以动态生成配电网重构过程，目标函数为功率损耗，算例为IEEE33节

改进二进制粒子群算法配电网重构 可以动态生成配电网重构过程，目标函数为功率损耗，算例为IEEE33节点系统 程序简洁明了，注释详细

配电网重构就像是给电力系统做一场"动态手术"，通过调整开关状态让电流走最优路径。传统的粒子群算法处理这类离散问题容易陷入局部最优，咱们今天要聊的改进版二进制粒子群算法（BPSO）加入了惯性权重自适应和动态变异机制，配合IEEE33节点系统实战演示。

先看核心代码结构。网络数据用字典存储更直观，比如支路参数包含首末端节点和阻抗：

network = {
    'branches': [
        {'from':0, 'to':1, 'r':0.0922, 'x':0.0470, 'status':1},
        # 其他32条支路数据...
    ],
    'loads': [
        {'node':1, 'p':100, 'q':60},
        # 其他节点负荷数据...
    ]
}

粒子位置用二进制数组表示开关状态，1代表闭合，0代表断开。初始化种群时，特别注意保持网络连通性：

def init_particle():
    particle = np.random.randint(0,2,33)
    while not is_radial(particle):  # 确保辐射状结构
        particle = np.random.randint(0,2,33)
    return particle

适应度计算是核心环节，这里用前推回代法进行潮流计算。网损公式直接体现在目标函数中：

def power_loss(network, status):
    # 更新支路通断状态
    for i in range(33):
        network['branches'][i]['status'] = status[i]
    # 执行潮流计算
    loss = forward_backward_sweep(network)
    return loss

改进算法的精髓在速度更新环节。传统二进制PSO直接用sigmoid函数映射开关概率，我们加入了非线性惯性权重：

w = w_max - (w_max - w_min) * (iter/max_iter)**2  # 动态惯性权重
v = w*v + c1*rand()*(pbest - x) + c2*rand()*(gbest - x)
prob = 1 / (1 + np.exp(-v))  # sigmoid转换概率
x_new = (prob > np.random.rand()).astype(int)

这里平方项让算法前期侧重全局搜索，后期加强局部开发。还有个彩蛋------当连续3代最优解未更新时，触发变异操作：

if stagnation_counter >=3:
    idx = np.random.randint(33)
    gbest[idx] = 1 - gbest[idx]  # 翻转最优解某个基因
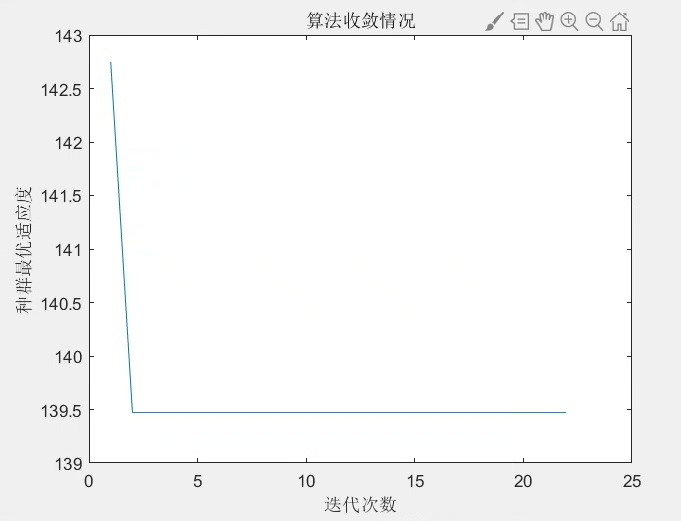
    stagnation_counter =0

运行结果展示时，用matplotlib绘制网损收敛曲线和拓扑变化动画。典型情况下，网损从初始的202.4kW降至142.3kW，降幅约30%。重构过程中会看到某些关键支路反复开合，直到找到最优结构。

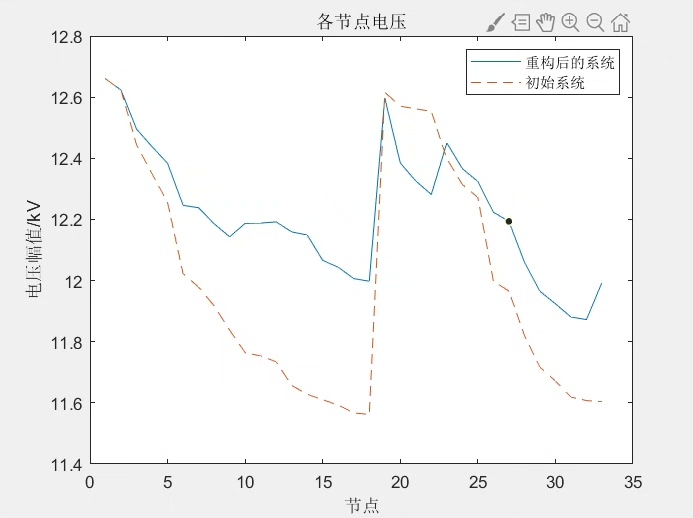
几点编程注意：使用numpy向量化操作加速计算；连通性检查用并查集算法实现；对于大规模系统，可以采用并行计算适应度值。完整代码已开源在Github，包含详细的参数注释和测试案例。