通俗理解神经网络的前向传播

引言

在当今的科技时代，人工智能（AI）已经渗透到我们生活的方方面面。从智能手机上的语音助手，到自动驾驶汽车，再到医疗诊断系统，这些神奇的技术背后，往往都有一个核心组件：神经网络。神经网络是模仿人类大脑结构的一种计算模型，它能够从数据中学习模式，并做出预测或决策。其中，前向传播（Forward Propagation）是神经网络的基本运行机制之一。它就像是神经网络的"思考过程"，从输入数据开始，一层一层地传递信息，最终得出输出结果。

为什么我们要理解前向传播呢？因为它是神经网络训练和推理的基础。如果你想入门深度学习，或者只是好奇AI是如何工作的，这篇文章将用通俗易懂的语言，结合图文解释，帮助你一步步掌握这个概念。我们会从生物灵感入手，逐步深入到数学细节，并通过例子和代码来加深理解。文章将尽量避免复杂的专业术语，用生活中的比喻来阐述。预计阅读完后，你会对神经网络的前向传播有一个清晰的认识。

神经网络的前向传播本质上是一个从输入到输出的计算流程。它不涉及学习（那是反向传播的事），而是单纯地"向前"传递数据。想象一下，你在厨房做菜：原材料（输入）经过切、炒、调味（隐藏层处理），最终变成一道美味佳肴（输出）。前向传播就是这个"做菜"的过程。

在深入之前，我们先来了解神经网络的起源和基本组成部分。

从生物神经元到人工神经元

人类大脑是由大约860亿个神经元组成的复杂网络。这些神经元通过突触连接，传递电化学信号，形成我们的思维、记忆和决策。20世纪中叶，科学家们受到大脑结构的启发，发明了人工神经网络（Artificial Neural Network，简称ANN）。

一个生物神经元大致包括树突（接收信号）、细胞体（处理信号）和轴突（输出信号）。在人工神经元中，我们简化了这个模型：输入信号通过权重（weights）加权求和，加上偏置（bias），然后经过激活函数（activation function）处理，产生输出。

用比喻来说，人工神经元就像一个"决策小人"。它接收多个输入（比如朋友的建议），每个输入有不同的重要性（权重），加上自己的偏好（偏置），然后决定是否行动（激活）。

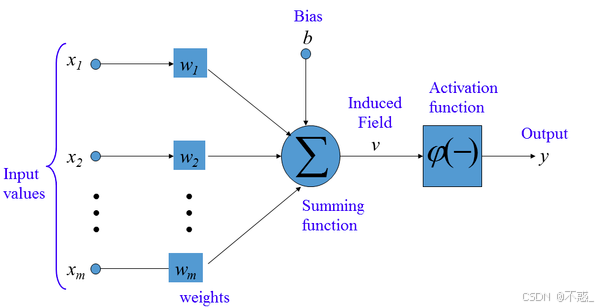
这个图像展示了人工神经元的典型模型：左侧是多个输入（x1, x2, ..., xn），每个输入乘以对应的权重（w1, w2, ..., wn），然后求和，加上偏置b，最后通过激活函数f输出y。

另一个视角：

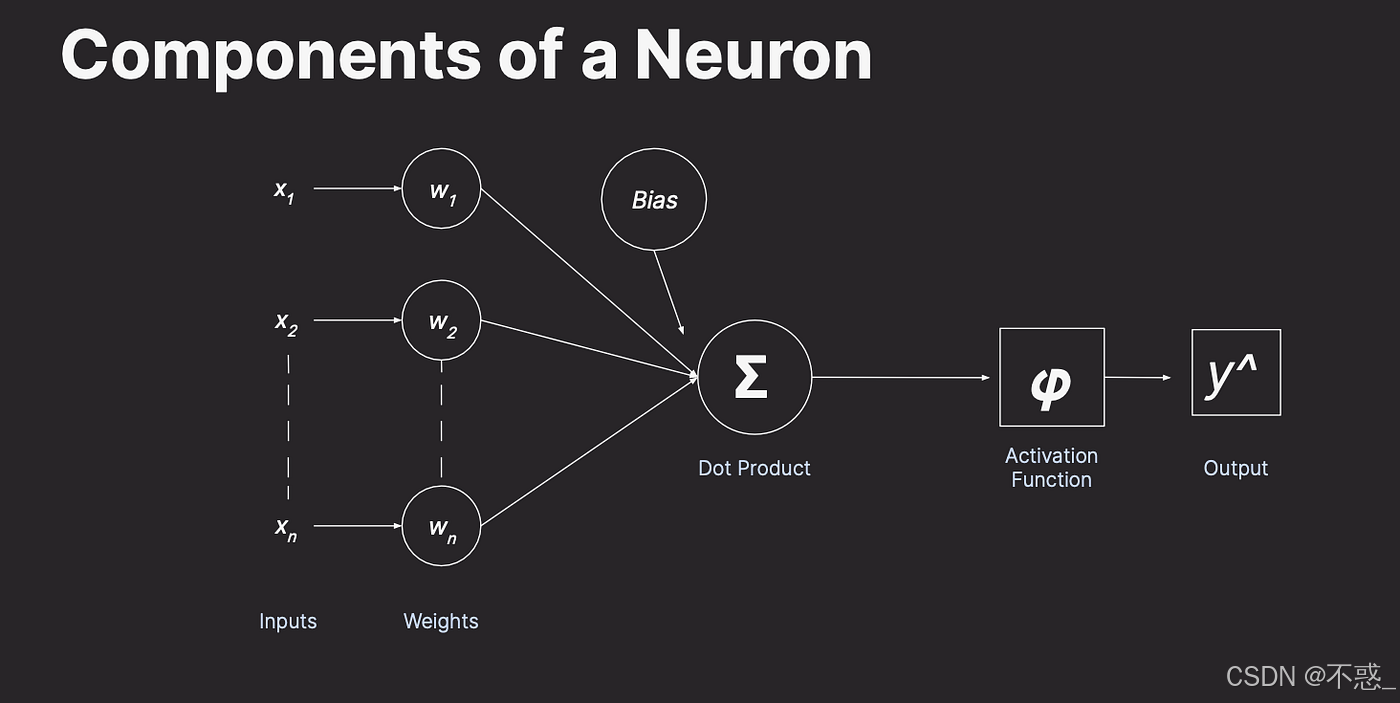
这里更详细地描绘了输入、权重、偏置和激活的过程。你可以看到，神经元不是简单的开关，而是能处理连续值的计算单元。

为什么需要激活函数？因为如果没有它，神经网络就只是线性变换，无法处理复杂问题。激活函数引入非线性，让网络能拟合任意函数。

常见的激活函数有Sigmoid，它将输入压缩到0到1之间，像一个"概率门"。

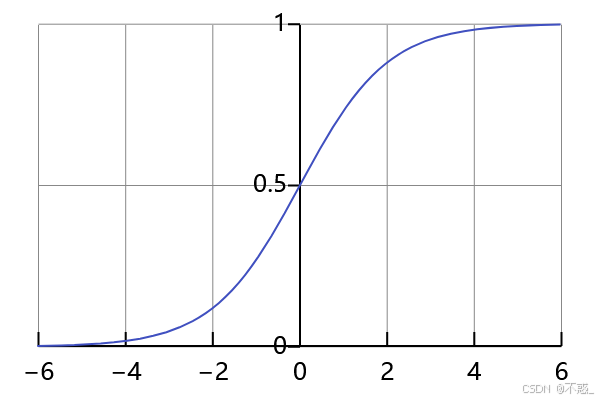
Sigmoid函数的图形是一个S形曲线，当输入很大时接近1，很小时接近0。这在早期神经网络中很流行，用于二分类问题。

另一种是ReLU（Rectified Linear Unit），它简单高效：如果输入大于0，就输出输入本身，否则输出0。

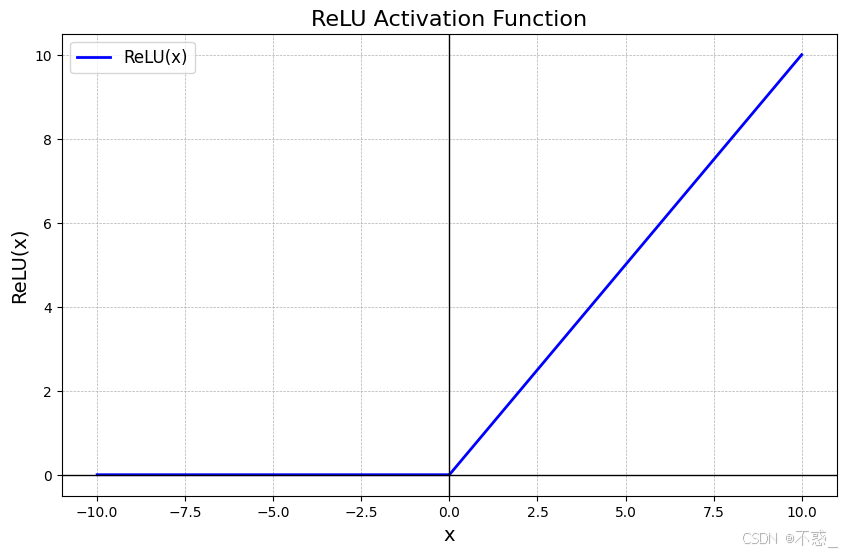
ReLU的图形像一个折线，避免了Sigmoid的梯度消失问题，在现代深度学习中广泛使用。

理解了单个神经元，我们就能构建更大的网络。

神经网络的基本结构

神经网络通常由多层神经元组成：输入层（Input Layer）、隐藏层（Hidden Layers）和输出层（Output Layer）。

输入层：接收原始数据，比如图像的像素值或房屋的面积、位置等特征。
隐藏层：中间处理层，可以有多层，每层有多个神经元，进行特征提取和变换。
输出层：产生最终结果，比如分类标签或预测数值。

一个简单的神经网络看起来像这样：

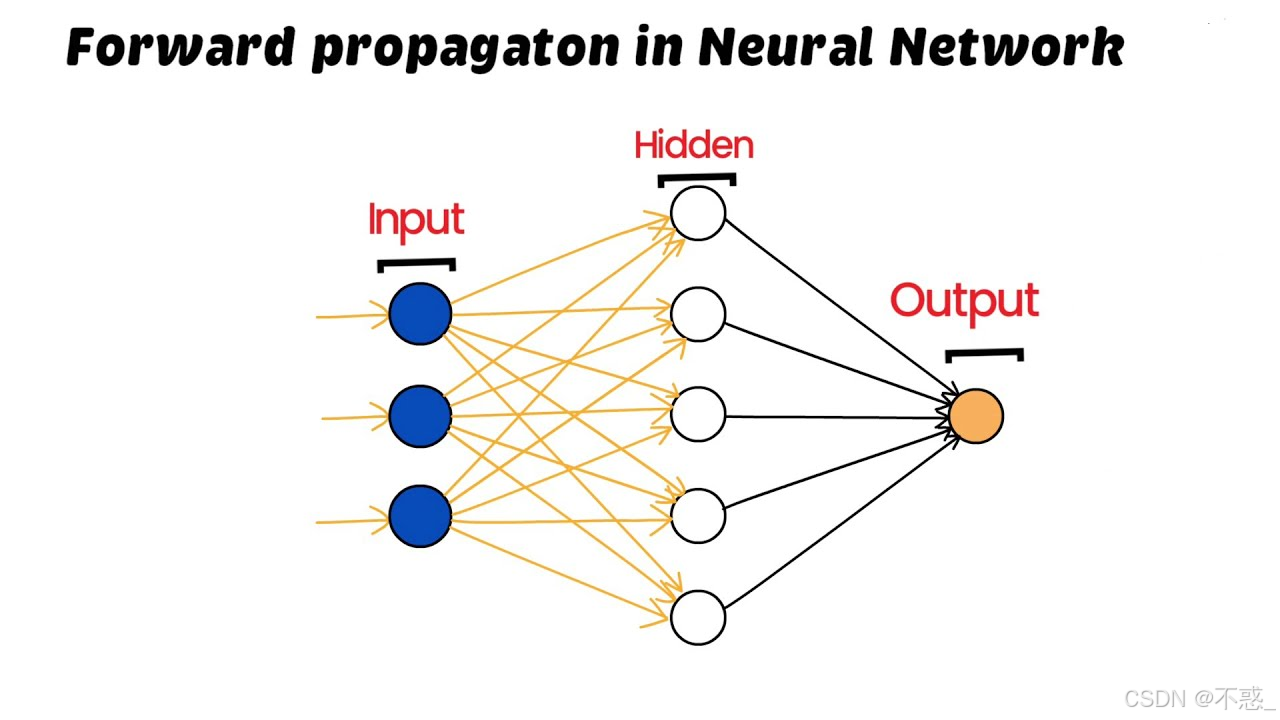
这个图展示了从输入到输出的前向传播路径。箭头表示信号的流动方向。

更复杂的多层网络：

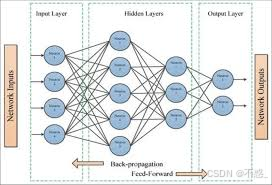
这里你可以看到Feedforward（前向）结构，没有循环。

神经网络的强大在于其层级结构。浅层提取简单特征（如边缘），深层组合成复杂模式（如物体）。

前向传播的概念

前向传播是神经网络从输入层到输出层的计算过程。它是"前向"的，因为信息只向前流动，不回头。

数学上，前向传播可以表述为：给定输入X，通过权重W和偏置B，一层一层计算激活值A，直到输出Y。

步骤：

初始化输入。
对于每一层：计算线性组合Z = W * A_prev + B，然后A = f(Z)，其中f是激活函数。
最后一层输出Y。

用生活比喻：想象一个公司决策流程。基层员工（输入层）收集数据，中层经理（隐藏层）分析加工，高层领导（输出层）做决定。信息从下到上流动，就是前向传播。

现在，我们深入单个神经元的前向传播。

单神经元的前向传播

假设一个神经元有两个输入x1和x2，权重w1和w2，偏置b。

第一步：加权求和 Z = x1w1 + x2w2 + b

第二步：激活 A = f(Z)

比如，用Sigmoid：f(Z) = 1 / (1 + e^{-Z})

假设x1=1, x2=2, w1=0.5, w2=0.3, b=0.1

Z = 10.5 + 20.3 + 0.1 = 0.5 + 0.6 + 0.1 = 1.2

A = 1 / (1 + e^{-1.2}) ≈ 0.768

这就是前向传播在单神经元上的实现。

图形表示：

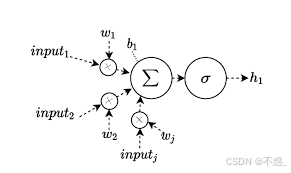
这个图强调了输入、权重、偏置和激活的交互。

如果没有激活函数，Z就是输出，但那样网络只能学线性关系，无法处理如XOR问题。

多层网络的前向传播

现在扩展到多层。假设一个三层网络：输入层2个节点，隐藏层3个节点，输出层1个节点。

表示为：

输入 X = $x1, x2$
第一层权重 W1 (3x2矩阵)，偏置 B1 (3x1)
隐藏层激活 A1 = f(W1 * X + B1)
第二层权重 W2 (1x3矩阵)，偏置 B2 (1x1)
输出 Y = f(W2 * A1 + B2)

前向传播就是依次计算A1和Y。

步步分解的图：

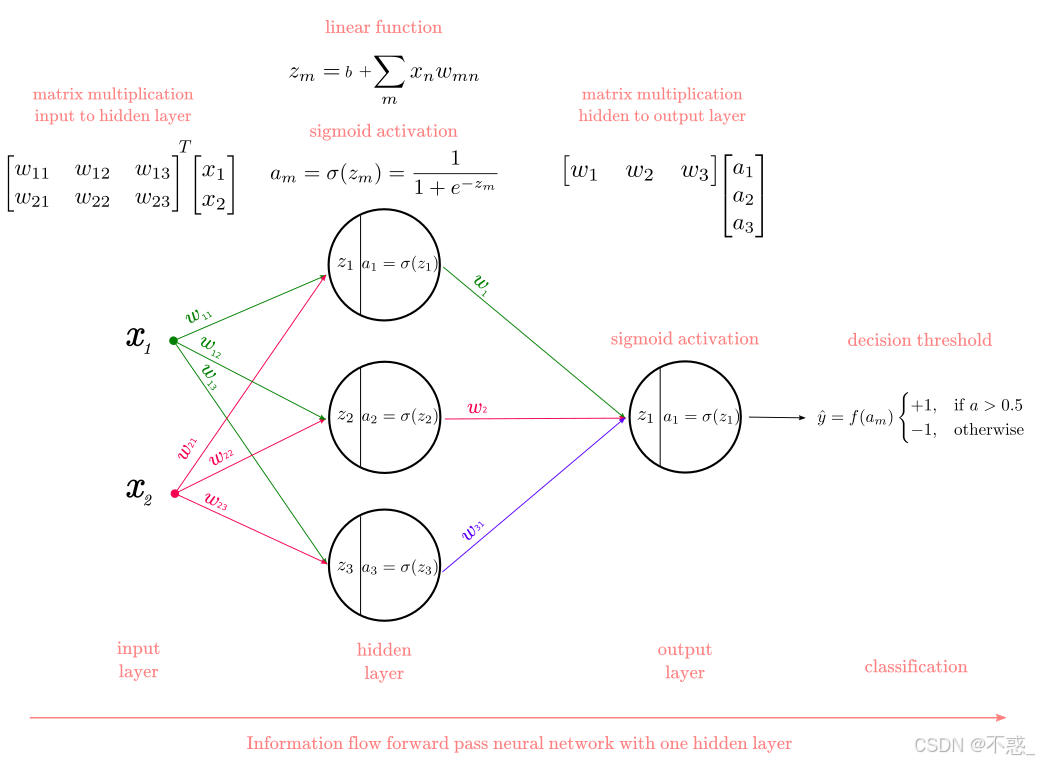
这个图像展示了多层感知器（MLP）的前向传播，每一步的计算。

另一个视图：

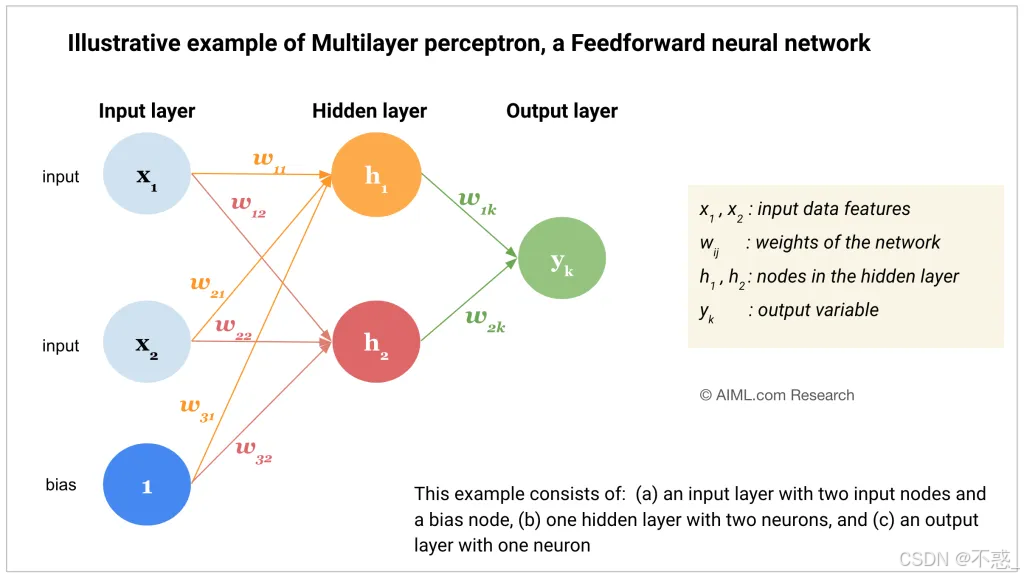
这里突出输入到隐藏到输出的流程。

在矩阵形式下，前向传播高效，因为可以用向量运算加速，尤其在GPU上。

数学表示和矩阵运算

为了通俗，我们用简单数学。

假设输入是列向量X (n x 1)，权重W (m x n)，偏置B (m x 1)

Z = W * X + B

A = f(Z)

f可以是元素-wise操作。

对于多层，用上标表示层：Z^[1](#1) = W^[2](#2) * A^[3](#3) + B^[4](#4)

A^[5](#5) = f(Z^[6](#6))

A^[7](#7) = X

Y = A^[8](#8)，L是总层数。

这让前向传播变得简洁。在代码中，用NumPy实现矩阵乘法。

为什么矩阵？因为实际数据是批量处理的，比如一批图像。X变成 (n x batch_size)矩阵。

一个简单例子：房价预测

假设我们用神经网络预测房屋价格。输入：面积（sqft）、卧室数。输出：价格。

简单网络：输入2，隐藏4，输出1。激活ReLU，最后线性。

随机权重：

W1 = $\[0.1, 0.2$ , $0.3, 0.4$ , $0.5, 0.6$ , $0.7, 0.8$ ]

B1 = $0.1, 0.1, 0.1, 0.1$

W2 = $\[0.1, 0.2, 0.3, 0.4$ ]

B2 = $0.1$

输入X = $1000, 3$ （1000平米，3卧室）

归一化后假设X = $0.5, 0.6$

Z1 = W1 * X + B1 = $0.1*0.5 + 0.2*0.6 +0.1, ...$ = 计算得 $0.27, 0.49, 0.71, 0.93$

A1 = ReLU(Z1) = $0.27, 0.49, 0.71, 0.93$ （全正）

Z2 = W2 * A1 + B2 = 0.10.27 + 0.2 0.49 + 0.30.71 + 0.40.93 + 0.1 ≈ 0.027 + 0.098 + 0.213 + 0.372 + 0.1 = 0.81

Y = 0.81（假设 scaled price）

这个例子展示了前向传播如何从特征到预测。

图形化：

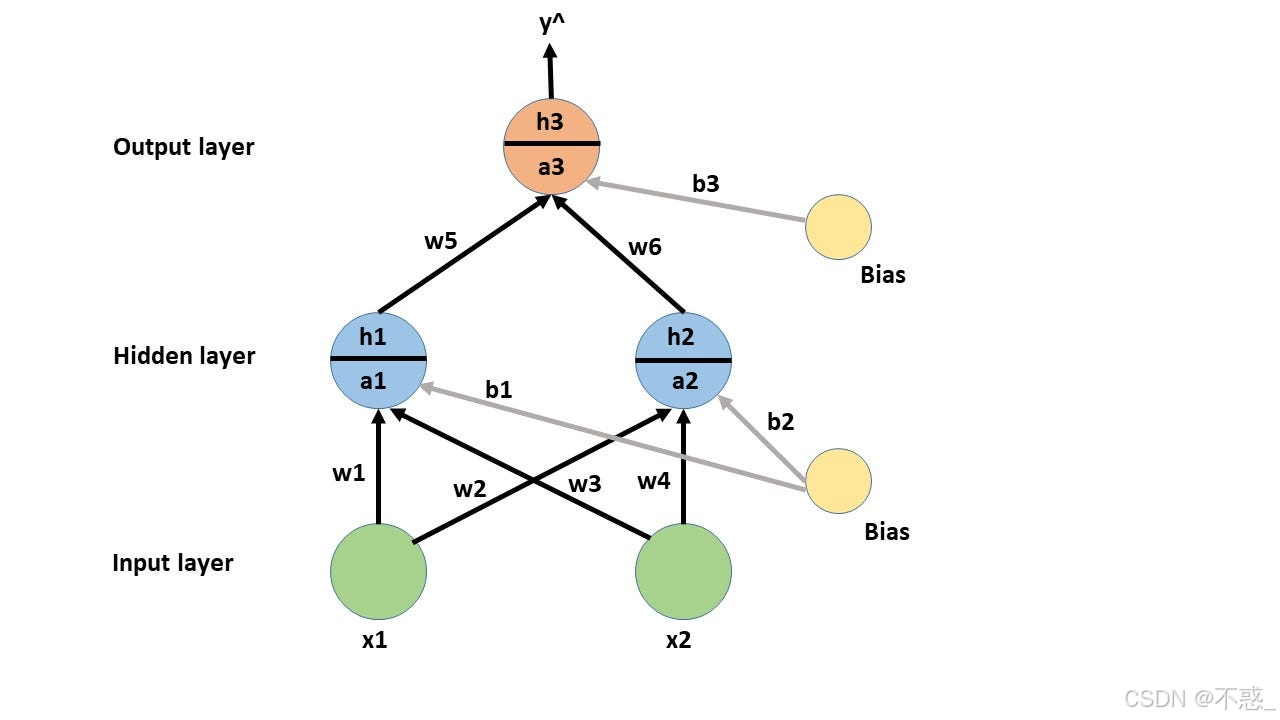
虽然不是房价专用，但展示了类似的前向传播。

另一个例子：图像分类

在MNIST数据集上，输入28x28像素=784，隐藏多层，输出10类（0-9数字）。

前向传播：像素值通过层，输出概率向量，用Softmax激活。

Softmax：将Z转为概率，sum=1。

例如，Z= $2,1,0$ -> Softmax ≈ $0.665, 0.245, 0.09$

最高概率的类是预测。

这个过程在手机人脸识别中类似。

步步图：

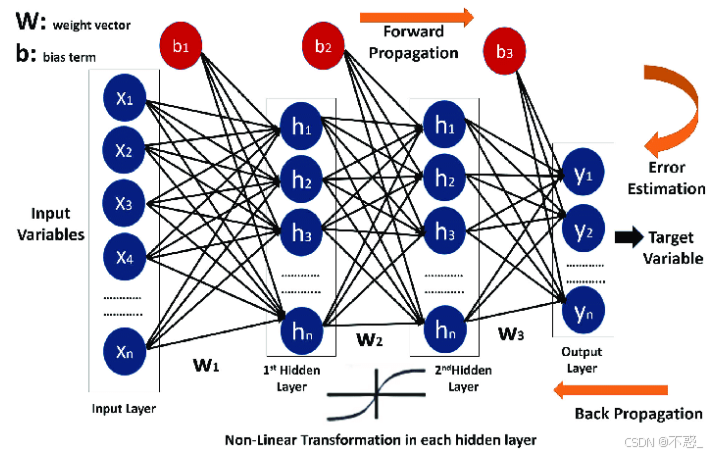
展示了MLP的前向传播。

代码实现

用Python简单实现一个前向传播。

import numpy as np

def sigmoid(z):

复制代码

return 1 / (1 + np.exp(-z))

def forward_propagation(X, W1, b1, W2, b2):

复制代码

Z1 = np.dot(W1, X) + b1

A1 = sigmoid(Z1)

Z2 = np.dot(W2, A1) + b2

A2 = sigmoid(Z2)

return A2

示例

X = np.array( $\[0.5$ , $0.6$ ])

W1 = np.array( $\[0.1, 0.2$ , $0.3, 0.4$ ])

b1 = np.array( $\[0.1$ , $0.1$ ])

W2 = np.array( $\[0.5, 0.6$ ])

b2 = np.array( $\[0.1$ ])

Y = forward_propagation(X, W1, b1, W2, b2)

print(Y) # 输出约 $\[0.645$ ]

这个代码展示了基本实现。在实际中，用框架如TensorFlow或PyTorch。

激活函数的选择

除了Sigmoid和ReLU，还有Tanh（-1到1），Leaky ReLU（负值小斜率）等。

Sigmoid图形：

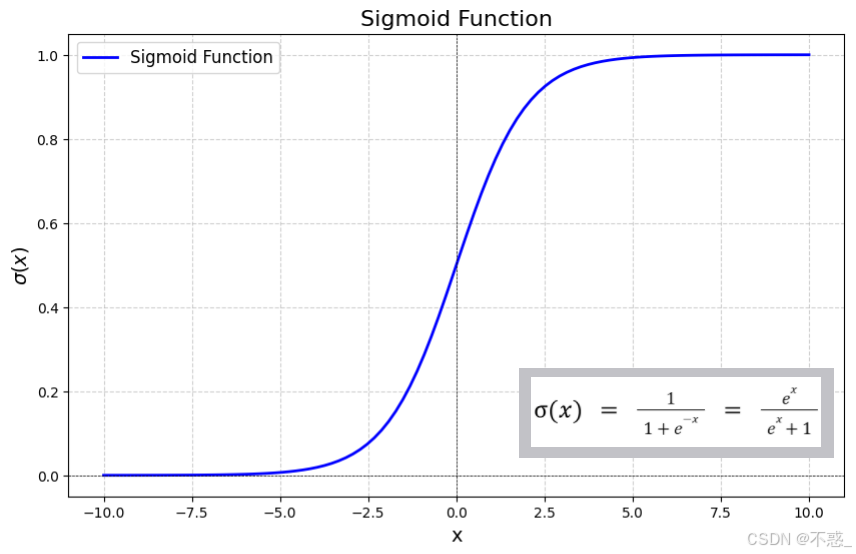
ReLU变体：

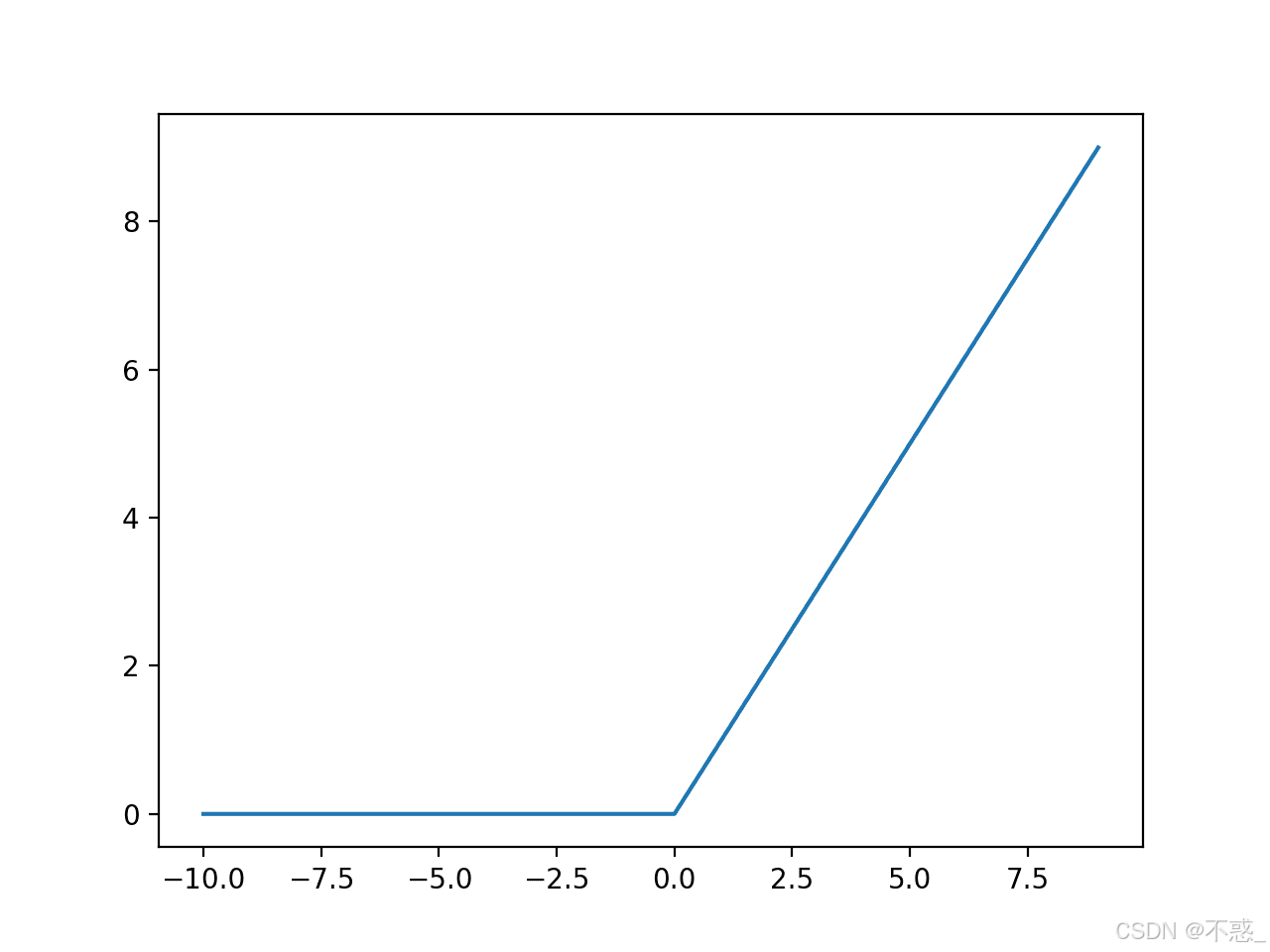
选择取决于任务：分类用Sigmoid/Softmax，回归用线性。

常见问题和误区

前向传播 vs 反向传播：前向是预测，反向是学习（更新权重）。
为什么多层？单层（感知器）只能线性分类，多层能非线性。
初始化重要：随机小值，避免饱和。
批处理：加速计算。
过拟合：太多层参数，需正则化。

误区：神经网络不是魔法，需要数据和计算资源。

高级话题简介

卷积神经网络（CNN）中，前向传播包括卷积和池化，用于图像。

循环神经网络（RNN）有时间维度，前向传播沿序列。

但基础仍是层级计算。

结语

通过这篇文章，我们从生物灵感到代码实现，通俗地理解了神经网络的前向传播。它是AI的核心引擎，帮助机器"思考"。希望这些解释和图像让你茅塞顿开。如果你想深入，建议实践简单模型。

前向传播看似简单，却支撑了ChatGPT等奇迹。未来，理解它将让你更好地把握AI时代。

l ↩︎
l ↩︎
l-1 ↩︎
l ↩︎
l ↩︎
l ↩︎
0 ↩︎
L ↩︎