本章节介绍如何估计动作价值函数。在第8.2节讨论了状态价值估计问题的基础上,本节重点将表格型Sarsa算法和表格型Q-learning算法扩展到函数逼近(值函数近似)的场景中。
一 Sarsa with function approximation
通过将状态价值替换为动作价值,可以很容易地从公式(8.13)推导出函数近似下的Sarsa算法。具体而言,假设用 来近似真实动作价值
。将(8.13)式中的状态价值估计
替换为动作价值估计
,即可得到参数更新规则(8.35)。
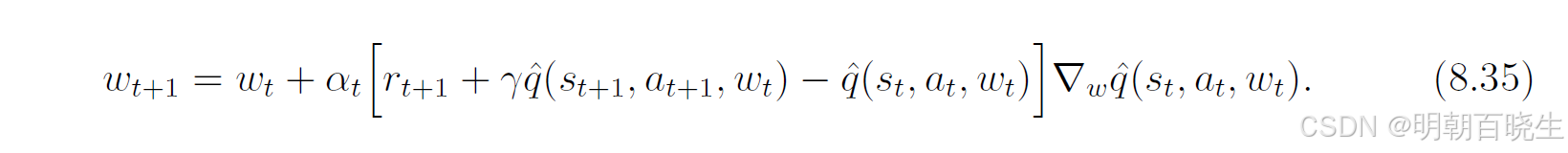
该算法的分析与(8.13)式类似。
当使用线性函数进行逼近时,有
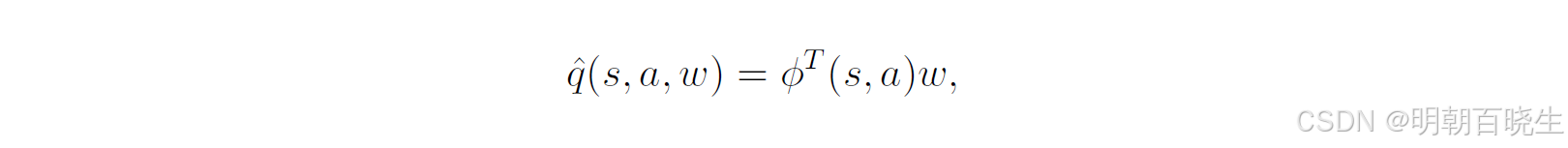
,其中 ϕ(s,a) 是特征向量。此时,梯度
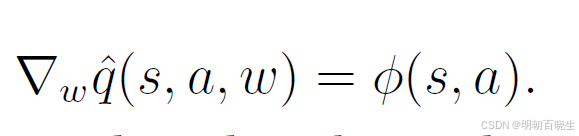
可以将(8.35)式的价值估计步骤与策略改进步骤相结合,以学习最优策略。该流程总结在算法8.2
中。

值得注意的是,虽然准确估计给定策略的动作价值需要多次运行(8.35)式,但在算法中,每次策略改进前只执行一次价值更新,这与表格型Sarsa算法是一致的。算法8.2旨在解决从特定起始状态到目标状态寻找良好路径的任务,因此它并不为所有状态寻找最优策略。然而,如果有足够多的经验数据,该实现过程可以很容易调整为为每个状态寻找最优策略。
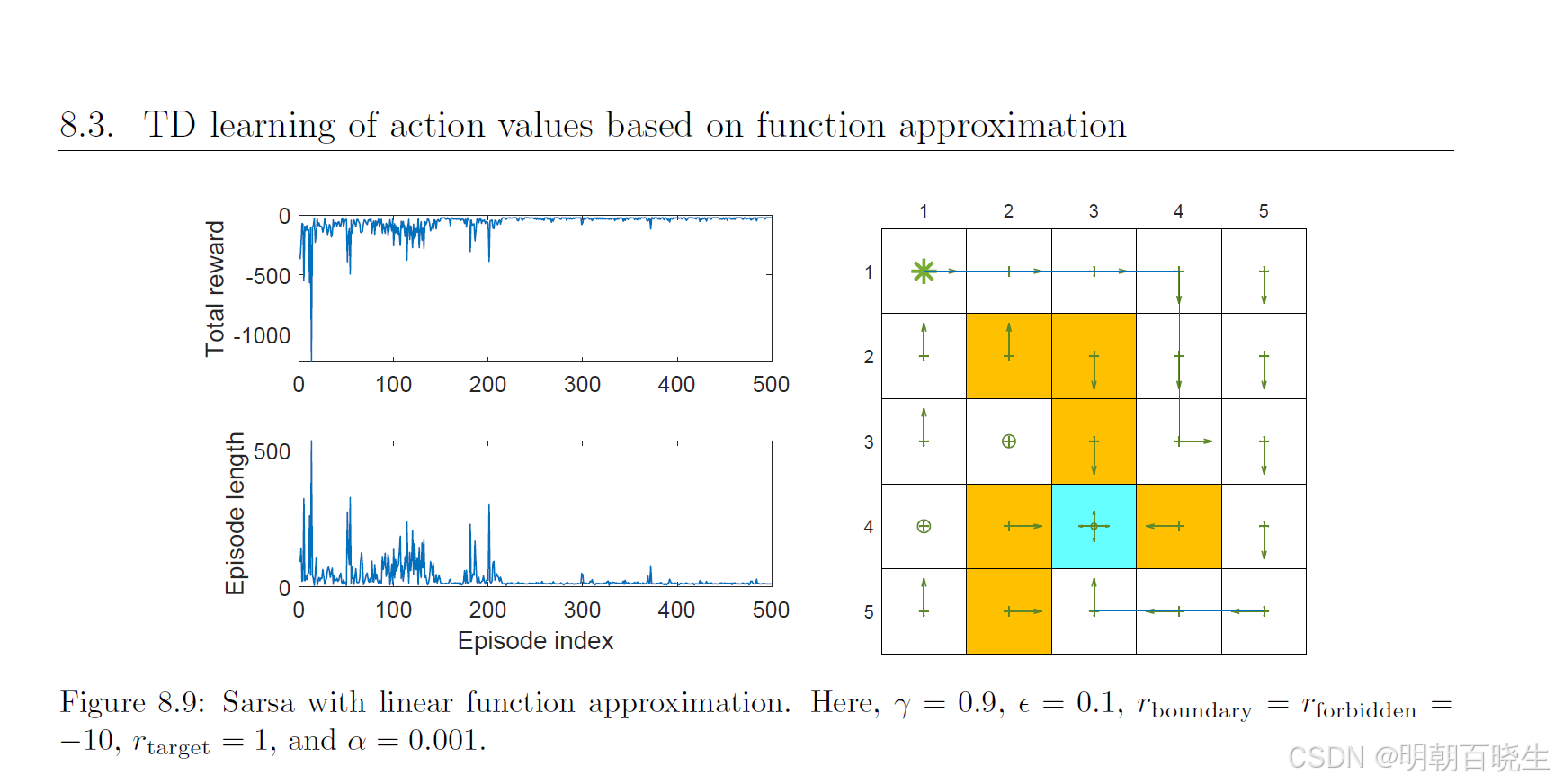
图8.9展示了一个示例,其任务是找到一个能从左上角状态引导智能体到达目标的策略。实验表明,每个回合的总奖励和长度都逐渐收敛到稳定值。该示例使用了5阶傅里叶线性特征向量。
二 Q-learning with function approximation
表格型Q-learning同样可以扩展到函数近似场景。其更新规则为公式(8.36)。
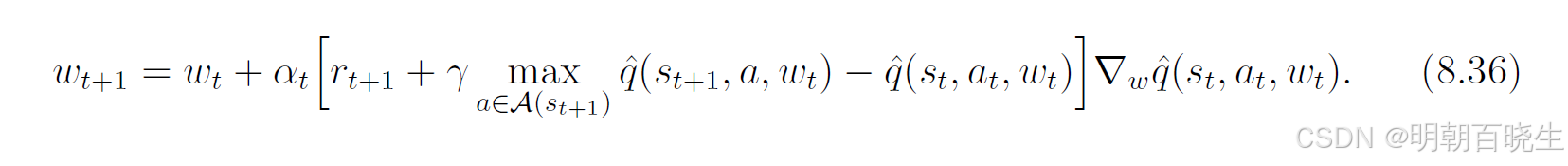
该规则与(8.35)式相似,主要区别在于用 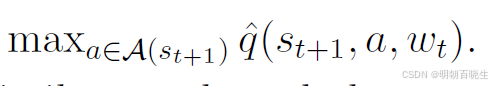 替代了原来
替代了原来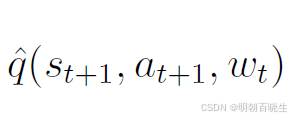
与表格型情况类似,(8.36)式可以以同策略或异策略的方式实现。算法8.3给出了一个同策略版本,

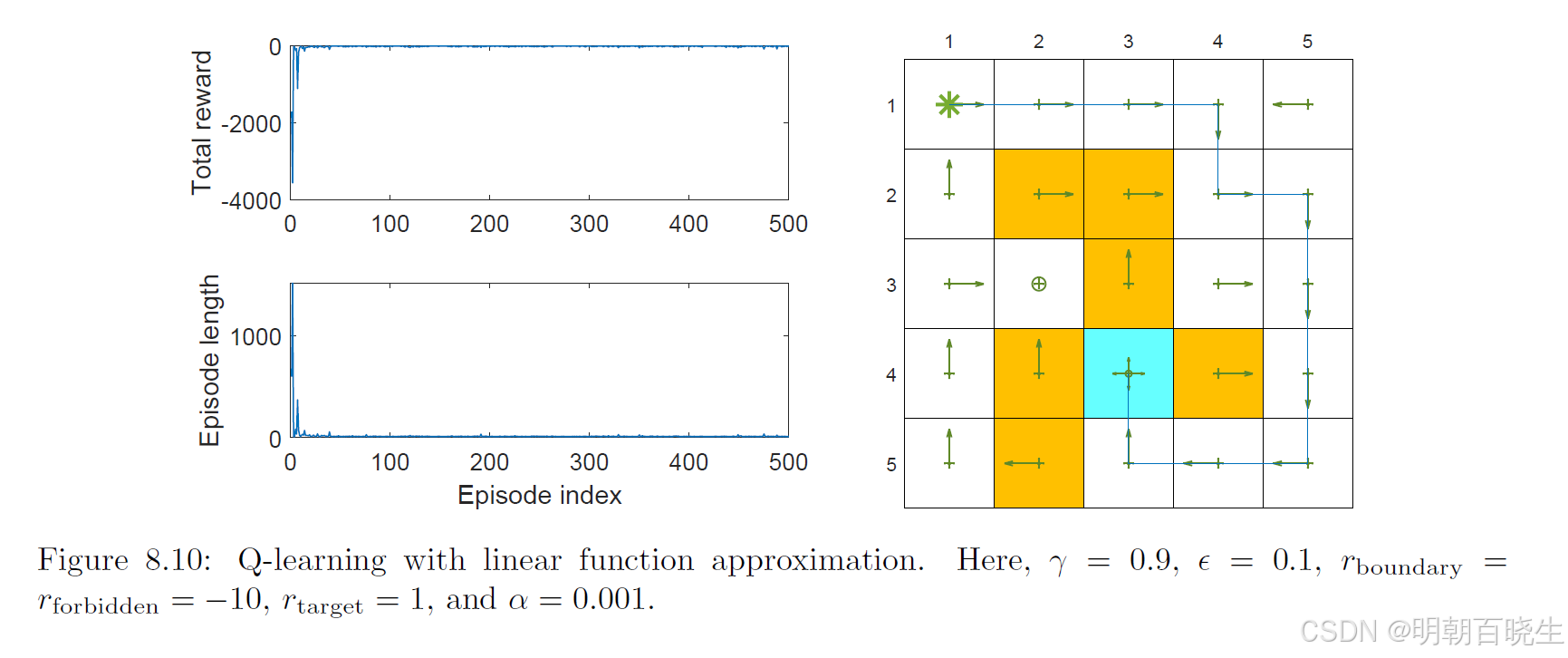
其演示示例如图8.10所示。该任务同样是从左上角状态寻找到达目标状态的良好策略。可以看出,采用线性函数近似的Q-learning能够成功学习到最优策略。该示例使用了五阶线性傅里叶基函数。异策略版本将在8.4节介绍深度Q-learning时进行演示。
在算法8.2和8.3中,虽然价值是用函数表示的,但策略 π(a∣s)仍然以表格形式表示。因此,它仍然假设状态和动作空间是有限的。在第9章中我们将看到,策略本身也可以用函数来表示,从而能够处理连续的状态和动作空间。
https://www.youtube.com/watch?v=VnpRp7ZglfA
https://www.youtube.com/watch?v=to-lHJfK4pw
https://www.bilibili.com/video/BV1sd4y167NS?spm_id_from=333.788.videopod.episodes&p=42