AI应用开发-Python:Embedding

1.向量表征(Vector Representation)

向量表征（Vector Representation）是核心概念之一。通过将文本、图像、声音、行为甚至复杂关系转化为高维向量（Embedding），AI系统能够以数学方式理解和处理现实世界中的复杂信息。这种表征方式为机器学习模型提供了统一的"语言"。

1.1 通俗理解：AI 的"语义坐标系"

想象一下，我们有一个巨大的"语义空间"，每个词或句子都被表示为一个点（向量）。语义越接近的词，在空间中的距离就越近。

例如：

"猫" 和 "狗" 的向量距离很近（都是宠物）
"飞机" 和 "火车" 距离较近（都是交通工具）
"猫" 和 "飞机" 距离很远

这种将文本转化为数字向量的过程，就叫 嵌入（Embedding）。

1.2 数学/几何中的向量

在最简单的层面上，一个向量就是一个具有大小和方向的量。物理学科上叫做矢量

例子：速度就是一个向量。如果你说"一辆车以 60 公里/小时的速度行驶"，这只是一个标量（只有大小）。但如果你说"一辆车以 60 公里/小时的速度向北行驶"，这就是一个向量（大小是 60，方向是北）。
可视化：在几何中，向量通常被画成一条带箭头的线段。线段的长度表示大小，箭头的指向表示方向。
坐标表示：在二维平面中，一个向量可以用一对数字 (x, y) 来表示，比如 (3, 4)。这表示从原点 (0,0) 出发，指向点 (3,4) 的箭头。在三维空间，就是 (x, y, z)

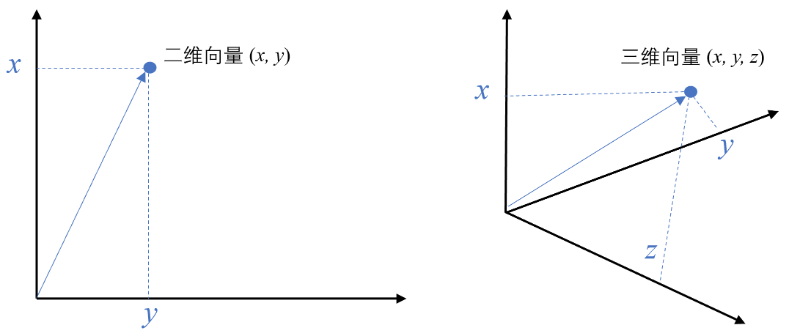
1.3 计算机科学中的向量

在计算机科学中，向量的含义被泛化了。它本质上就是一个一维数组 ，即一列有序的数字。

例子：[1.5, -0.2, 3.14, 42.0] 就是一个包含 4 个数字的向量。
维度的含义 ：这个向量的维度就是它包含的数字个数。上面的例子是 4 维向量。在机器学习和AI中，我们经常会处理几百、几千甚至更高维度的向量。

在计算机的世界里，我们可以用这样一个数字列表（向量）来表示任何东西 。每个数字可以被看作是描述该事物的一个特征或属性。

用向量表示一杯饮料：

特征1：甜度 (0 不甜，10 非常甜) -> 7
特征2：酸度 (0 不酸，10 非常酸) -> 2
特征3：温度 (0 冰，10 烫) -> 1
特征4：咖啡因含量 (毫克) -> 90

那么，这杯饮料就可以表示为一个 4 维向量：[7, 2, 1, 90]。这杯饮料很可能是一杯冰甜咖啡。

1.4 向量Embedding

向量嵌入 是"向量"概念的一个非常强大和重要的应用。它是一种特殊类型的向量 ，专门用于在计算机中表示复杂对象 （如词语、图片、声音、用户、商品等），并捕捉其内在含义 或语义。

你可以把向量嵌入理解为一个对象的 "数字指纹" 或 "DNA序列"。

向量嵌入的强大之处在于，它不仅仅是随机的一堆数字，而是通过复杂的机器学习模型（如 Word2Vec, Transformer 等）学习得到的。这些数字的排列方式具有以下关键特性：

语义相似性
- 含义相近的对象，它们的向量在空间中的距离会很近。
- 例子： "猫"和"狗"都是宠物，它们的向量距离会很近；而"猫"和"电脑"的向量距离会很远。
关系类比
- 向量空间中可以捕捉到类比关系。最著名的例子是：
  - "国王"的向量 - "男人"的向量 + "女人"的向量 ≈ "女王"的向量
- 这意味着词语之间的语义关系（如"性别关系"）被编码在了向量的数学运算中。

1.5 向量嵌入是如何工作的？（以词嵌入为例）

想象一下，我们要把词语映射到一个 3 维空间（实际中维度更高，如300维、768维），以便可视化：

初始状态：一开始，计算机随机给每个词分配一个位置（一个向量）。
学习过程 ：模型阅读海量文本（如维基百科）。它学习一个原则："出现在相似上下文中的词语，具有相似的含义" 。
- 例如，"苹果"和"香蕉"经常出现在"吃"、"水果"、"甜"等词语附近。
- 而"苹果"和"微软"可能出现在"公司"、"技术"等词语附近。
最终结果 ：经过学习，模型会调整每个词的向量位置。
- "苹果"（水果）和"香蕉"、"橘子"的向量会聚集在一起。
- "苹果"（公司）和"微软"、"谷歌"的向量会聚集在另一处。
- "水果"这个大类会和"蔬菜"等大类在更高层级上靠近。

最终，我们得到了一个"语义地图"，每个词都是这张地图上的一个点（即一个高维向量）。

1.6 Embedding 的核心价值

作用	说明
语义搜索	搜索"轻便的户外背包"也能匹配"登山用小容量背包"
自然语言处理	搜索引擎（理解你的查询意图）、机器翻译、智能客服、情感分析。
图像识别	将图片转换为向量，然后寻找相似的图片。
推荐系统	根据用户兴趣向量推荐相似内容
RAG 基础	检索最相关的知识片段，供大模型参考生成答案

2.向量间相似度计算

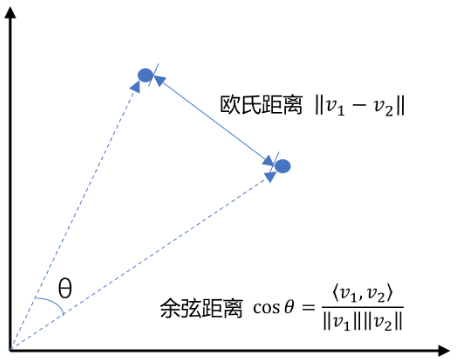
余弦相似度是通过计算两个向量夹角的余弦值来衡量相似性，等于两个向量的点积除以两个向量长度的乘积。

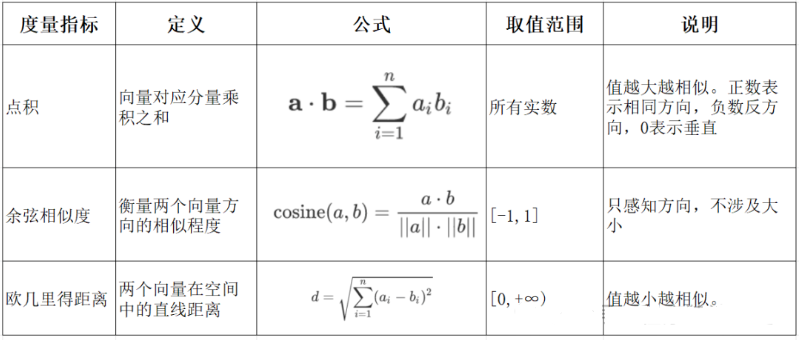
2.1 实验环境准备

获取API KEY

通过代码实验需要用到 Embedding 模型，这里接入的是阿里百炼平台模型。到阿里百炼https://bailian.console.aliyun.com/ 注册账号后，生成一个 API_KEY 就可以使用了。

将API KEY配置到环境变量中

参考文档：https://bailian.console.aliyun.com/?tab=api#/api/?type=model&url=2803795

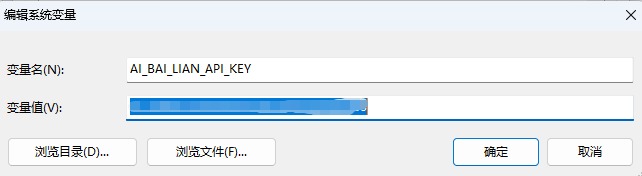
这里我注册的环境变量名称为：AI_BAI_LIAN_API_KEY

安装依赖

现在需要安装两个python 库：

numpy 用于做数值计算，它扩展了很多数据类型
openai 它提供了与 openai 兼容的 API库，可以用来访问各种AI平台提供的模型服务。

shell 复制代码

# pip install --upgrade numpy openai
pip install numpy openai

2.2 Embedding Model

嵌入模型（Embedding Model）是一种将离散数据（如文本、图像）映射到连续向量空间的技术。通过高维向量表示（如 768 维或 3072 维），模型可捕捉数据的语义信息，使得语义相似的文本在向量空间中距离更近。例如，"忘记密码"和"账号锁定"会被编码为相近的向量，从而支持语义检索而非仅关键词匹配。

核心作用：

**语义编码：**将文本、图像等转换为向量，保留上下文信息（如 BERT 的 CLS Token 或均值池化。相似度计算：通过余弦相似度、欧氏距离等度量向量关联性，支撑检索增强生成（RAG）、推荐系统等应用、
**信息降维：**压缩复杂数据为低维稠密向量，提升存储与计算效率。

2.2.1 通义千问Embedding

百炼平台已经为我们提供好了模型：操作路径：

模型服务（在顶部左上角）->全部模型->模态类型 -> 向量 -> 文本向量->[通义千问-Embedding]

查看 API 参考，选择 OpenAI 兼容接口/Python:

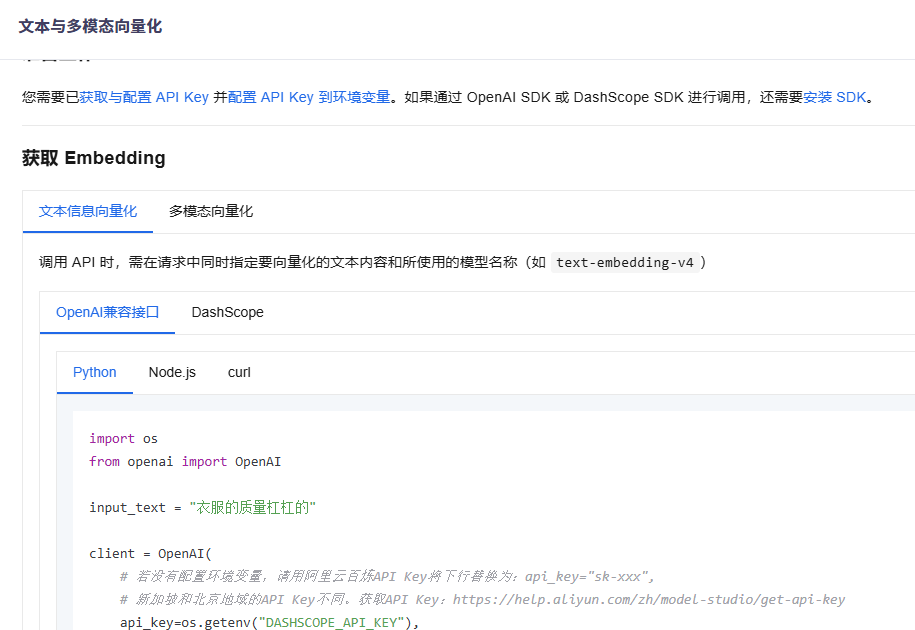
2.2.2 主流嵌入模型分类

Embedding 模型将文本转换为数值向量，捕捉语义信息，使计算机能够理解和比较内容的"意义"。选择 Embedding 模型的考虑因素：

因素	说明
任务性质	匹配任务需求(问答、搜索、聚类等)
领域特性	通用vs专业领域(医学、法律等)
多语言支持	需处理多语言内容时考虑
维度	权衡信息丰富度与计算成本
许可条款	开源vs专有服务
最大Tokens	适合的上下文窗口大小

1. 通用全能型

**BGE-M3：**北京智源研究院开发，支持多语言、混合检索（稠密+稀疏向量），处理 8K 上下文，适合企业级知识库。
**NV-Embed-v2：**基于 Mistral-7B，检索精度高（MTEB 得分 62.65），但需较高计算资源。

2. 垂直领域特化型

中文场景： BGE-large-zh-v1.5 （合同/政策文件）、 M3E-base （社交媒体分析）。
多模态场景： BGE-VL （图文跨模态检索），联合编码 OCR 文本与图像特征。

3. 轻量化部署型

**nomic-embed-text：**768 维向量，推理速度比 OpenAI 快 3 倍，适合边缘设备。
**gte-qwen2-1.5b-instruct：**1.5B 参数，16GB 显存即可运行，适合初创团队原型验。

中文为主 → BGE 系列 > M3E；

多语言需求 → BGE-M3 > multilingual-e5；

预算有限 → 开源模型（如 Nomic Embed）

2.3 通用包

代码中创建一个通用包common这个包下提供两个通用函数：

创建openai 客户端
获取embedding模型

common/model_utils.py

python 复制代码

import os
from openai import OpenAI

def _get_client():
    api_key = os.getenv("AI_BAI_LIAN_API_KEY")
    base_url="https://dashscope.aliyuncs.com/compatible-mode/v1"
    return OpenAI(api_key=api_key,base_url=base_url)

def get_embedding(text, model="text-embedding-v4"):
    """
    获取embedding向量，默认使用 text-embedding-v4
    """
    client = _get_client
    # 判断text是不是一个列表
    if isinstance(text, list):
        return  client.embeddings.create(input = text, model=model)
    text = text.replace("\n", " ")
    return client.embeddings.create(input = [text], model=model)

2.4 文本转向量

在main函数中我们输入一小段文字，使用模型进行向量化：

python 复制代码

from common import model_utils
if __name__ == '__main__':
    text="今天天气不错"
    response=model_utils.get_embedding(text)
    # {"data":[{"embedding":[-0.05972001701593399,-0.039419323205947876,...],"index":0,"object":"embedding"}],"model":"text-embedding-v4","object":"list","usage":{"prompt_tokens":4,"total_tokens":4},"id":"2d62a3a3-a97e-9f42-9b4a-1dfdccc32c50"}
    print(response.model_dump_json())
    # [[-0.05972001701593399, -0.039419323205947876, 0.026300963014364243]]
    result=response.data[0].embedding
    print(result[:3]) # 打印前三个
    # 默认维度为 1024
    print(len(result))

打印出来的数组元素为 1024 个，即默认是1024 个温度

2.5 距离计算

现在在common/model_utils.py中继续添加两个函数，分别用于计算余弦距离和欧式距离

在这之前，我们先要熟悉一个 nump 中的两个函数 dot和 norm

2.5.1 点积(dot)

dot 函数主要用于计算两个数组的点积（Dot Product） 。 对于一维向量： 它计算的是对应元素的乘积之和。

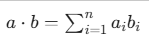
python 复制代码

import numpy as np
from numpy import dot

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

result = dot(a, b)  # (1*4) + (2*5) + (3*6) = 4 + 10 + 18 = 32
print(result)

对于二维矩阵： 它执行的是标准的矩阵乘法。 ( "行乘列"的运算规则。 )

假设有两个 2x2 矩阵相乘：

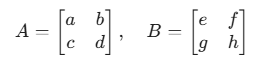
2.5.2 范数/长度 (norm)

norm 函数用于计算向量或矩阵的范数。在处理向量时，默认计算的是 L2 范数（欧几里得长度），即向量在空间中的物理长度。

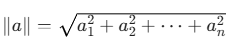
python 复制代码

from numpy.linalg import norm

a = np.array([3, 4])
dist = norm(a)  # sqrt(3^2 + 4^2) = sqrt(9 + 16) = 5.0
print(dist)

2.5.3 余弦相似度计算

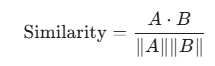
python 复制代码

import numpy as np
from numpy import dot
from numpy.linalg import norm

def cosine_similarity(v1, v2):
    return dot(v1, v2) / (norm(v1) * norm(v2))

# 示例：比较两个文档向量或嵌入向量
vec1 = np.array([1, 1, 0])
vec2 = np.array([1, 0, 1])

similarity = cosine_similarity(vec1, vec2)
print(f"相似度: {similarity:.4f}")

2.5.4 欧式距离

python 复制代码

def l2(a, b):
    '''欧氏距离 -- 越小越相似'''
    x = np.asarray(a)-np.asarray(b)
    return norm(x)

2.6 相似度对比

下面我们将三句话进行向量化，然后对比它们之间的相似度：

python 复制代码

text1="Spring AI 帮助开发者快速集成人工智能功能"
text2="Spring AI 是一个用于构建 AI 应用的框架"
text3="Java 是一种跨平台的编程语言"

text_list=[text1,text2,text3]
# 获取向量
response_data = model_utils.get_embedding(text_list).data
# 将response_data 中的 embedding 提取成一个二维数组
embedding_list = [data.embedding for data in response_data]
# 余弦相似度对比
print(f"text1 与 text2 余弦距离:{model_utils.cosine_similarity(embedding_list[0], embedding_list[1])}")
print(f"text1 与 text3 余弦距离:{model_utils.cosine_similarity(embedding_list[0], embedding_list[2])}")
print(f"text2 与 text3 余弦距离:{model_utils.cosine_similarity(embedding_list[1], embedding_list[2])}")

print("="*50)
# 欧式距离对比
print(f"text1 与 text2 欧式距离:{model_utils.l2(embedding_list[0], embedding_list[1])}")
print(f"text1 与 text3 欧式距离:{model_utils.l2(embedding_list[0], embedding_list[2])}")
print(f"text2 与 text3 欧式距离:{model_utils.l2(embedding_list[1], embedding_list[2])}")

输出:

latex 复制代码

text1 与 text2 余弦距离:0.8747069083399994
text1 与 text3 余弦距离:0.31450617230698164
text2 与 text3 余弦距离:0.373276450524592
==========================================
text1 与 text2 欧式距离:0.5005858686858007
text1 与 text3 欧式距离:1.1708918177413983
text2 与 text3 欧式距离:1.1195745555537098

余弦值越大，说明夹角越小，则越相似( cos(0) =1 ), 很明显 text1与 text2 是最相似的。
距离越小，说明，两个向量相聚越小，则越相似，显然 text1与 text2 之间的距离比较小。

3.向量数据库

向量数据库，是专门为向量检索设计的中间件！高效存储、快速检索和管理高纬度向量数据的系统称为向量数据库

向量数据库的核心作用是实现相似性搜索，即通过计算向量之间的距离（如欧几里得距离、余弦相似度等）来找到与目标向量最相似的其他向量。它特别适合处理非结构化数据，支持语义搜索、内容推荐等场景。

核心功能：

向量存储
相似性度量
相似性搜索

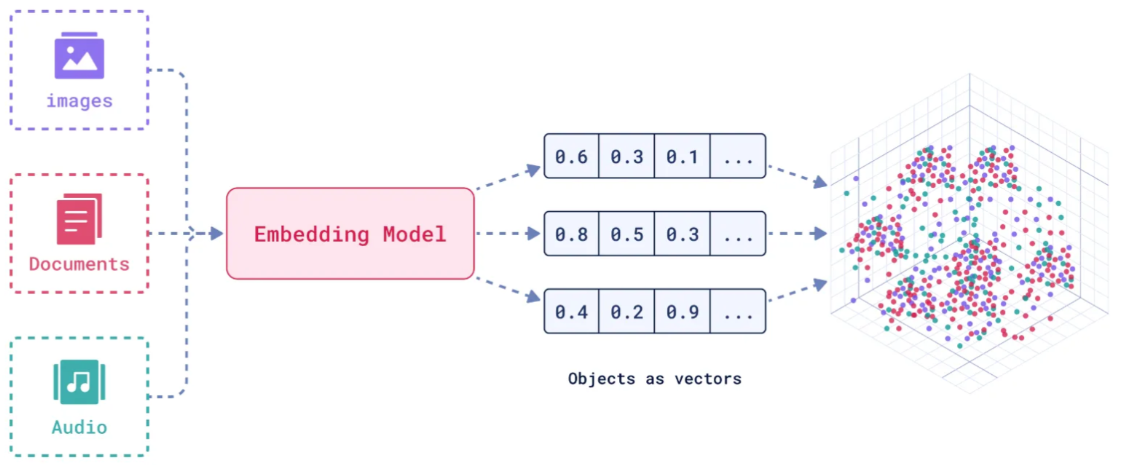
注意 text Embedding model 只能对文本向量化，对于 image 和 audio 则需要其它多模态模型

3.1 向量数据库与传统数据库

数据类型

传统数据库：存储结构化数据（如表格、行、列）。
向量数据库：存储高维向量数据，适合非结构化数据。

查询方式

传统数据库：依赖精确匹配（如=、<、>）。
向量数据库：基于相似度或距离度量（如欧几里得距离、余弦相似度）。

应用场景

传统数据库：适合事务记录和结构化信息管理。
向量数据库：适合语义搜索、内容推荐等需要相似性计算的场景。

注意：

向量数据库的意义是快速的检索；

向量数据库本身不生成向量，向量是由 Embedding 模型产生的；

向量数据库与传统的关系型数据库是互补的，不是替代关系，在实际应用中根据实际需求经常同时使用。

主流向量数据库：

数据库	类型	核心特点
Milvus	开源 + 云	功能全面、支持多种索引和分布式部署，适合大规模生产环境。
Pinecone	商业 SaaS	全托管、API 简单易用，适合快速开发，但不开源、需联网。
Weaviate	开源 + 企业版	内置语义搜索与知识图谱能力，支持 GraphQL，上手容易。
Qdrant	开源 + 云	性能优秀、支持过滤和集群，Rust 编写，部署简单。
Chroma	开源	轻量级，专为 LLM 应用设计，与 LangChain 深度集成，适合原型或小项目。
FAISS	开源库（非数据库）	Meta 出品，高效向量检索，但无持久化或服务功能，常用于研究或嵌入其他系统。
Vespa	开源	Yahoo 出品，支持实时搜索、排序和向量混合查询，适合复杂业务逻辑。
Redis（带向量模块）	开源 + 商业	在 Redis 中添加向量搜索能力，适合已有 Redis 架构、要求低延迟的场景。

3.2 Chroma向量数据库

官方文档：https://docs.trychroma.com/docs/overview/introduction

Chroma 是一款开源的向量数据库，专为高效存储和检索高维向量数据设计。其核心能力在于语义相似性搜索，支持文本、图像等嵌入向量的快速匹配，广泛应用于大模型上下文增强（RAG）、推荐系统、多模态检索等场景。与传统数据库不同，Chroma 基于向量距离（如余弦相似度、欧氏距离）衡量数据关联性，而非关键词匹配。

轻量易用：以 Python/JS 包形式嵌入代码，无需独立部署，适合快速原型开发。
灵活集成：支持自定义嵌入模型（如 OpenAI、HuggingFace），兼容 LangChain 等框架。
高性能检索：采用 HNSW 算法优化索引，支持百万级向量毫秒级响应。
多模式存储：内存模式用于开发调试，持久化模式支持生产环境数据落地。

3.2.1 安装Chroma

shell 复制代码

pip install chromadb

3.2.2 内存运行模式

参考文档：https://docs.trychroma.com/docs/run-chroma/ephemeral-client

python 复制代码

import chromadb

client = chromadb.EphemeralClient()

3.2.3 持久化运行模式

参考文档： https://docs.trychroma.com/docs/run-chroma/persistent-client

python 复制代码

import chromadb

client = chromadb.PersistentClient(path="/path/to/save/to")

3.2.4 Chroma操作流程

集合是 Chroma 中管理数据的基本单元，类似关系数据库的表

创建集合

python 复制代码

import chromadb
from chromadb.utils import embedding_functions
if __name__ == '__main__':
    # 数据保存至本地目录
    client = chromadb.PersistentClient(path="./chroma")
    # 默认情况下，Chroma 使用 DefaultEmbeddingFunction，它是基于 Sentence Transformers 的 MiniLM-L6-v2 模型
    default_ef = embedding_functions.DefaultEmbeddingFunction()
    collection = client.create_collection(
        name="my_collection",
        configuration={
            # HNSW 索引算法，基于图的近似最近邻搜索算法（Approximate Nearest Neighbor，ANN）
            "hnsw": {
                "space": "cosine",  # 指定余弦相似度计算
                "ef_search": 100,
                "ef_construction": 100,
                "max_neighbors": 16,
                "num_threads": 4
            },
            # 指定向量模型
            "embedding_function": default_ef
        }
    )

方法执行后，发现本地创建了一个文件 chroma/chroma.sqlite3,数据将会被持久化到这个文件中。

client.create_collection方法其实只需要给定一个 name参数即可，其它参数都有默认值。上面代码中给定的就是默认值。

python 复制代码

    # 如果集合不存在，则创建
    collection=client.get_collection(name="my_collection")
    if  collection is None:
        # 会自动下载 内置模型 all-MiniLM-L6-v2
        collection = client.create_collection(name="my_collection")

查询集合

python 复制代码

collection = client.get_collection(name="my_collection")
print(collection.peek()) #  returns a list of the first 10 items in the collection.
print(collection.count()) # returns the number of items in the collection.
modify() #  rename the collection

删除集合

python 复制代码

client.delete_collection(name="my_collection")

添加数据

python 复制代码

# 方式1：自动生成向量（使用集合指定的嵌入模型）
collection.add(
    # 文档的集合
    documents = ["RAG是一种检索增强生成技术", "向量数据库存储文档的嵌入表示", "在机器学习领域，智能体（Agent）通常指能够感知环境、做出决策并采取行动以实现特定目标的实体"],
    # 文档元数据信息
    metadatas = [{"source": "RAG"}, {"source": "向量数据库"}, {"source": "Agent"}],
    # id
    ids = ["id1", "id2", "id3"]
)

# 方式2：手动传入预计算向量（实际开发中推荐使用）
# collection.add(
#     embeddings = get_embeddings("RAG是什么？")
#     documents = ["文本1", "文本2"],
#     ids = ["id3", "id4"]
# )

用向量模型将数据向量化以后存入也是可以的

数据管理

python 复制代码

# 更新集合中的数据：
collection.update(ids=["id1"], documents=["RAG是一种检索增强生成技术，在智能客服系统中大量使用"])

# 删除集合中的数据：
collection.delete(ids=["id3"])

数据查询

python 复制代码

results = collection.query(
    query_texts = ["RAG是什么？"],
    n_results = 3, # 结果指定为3个。
    # where = {"source": "RAG"}, # 按元数据过滤
    # where_document = {"$contains": "检索增强生成"} # 按文档内容过滤
)

print(results)