机器学习——支持向量机（SVM）

SVM的基本概念

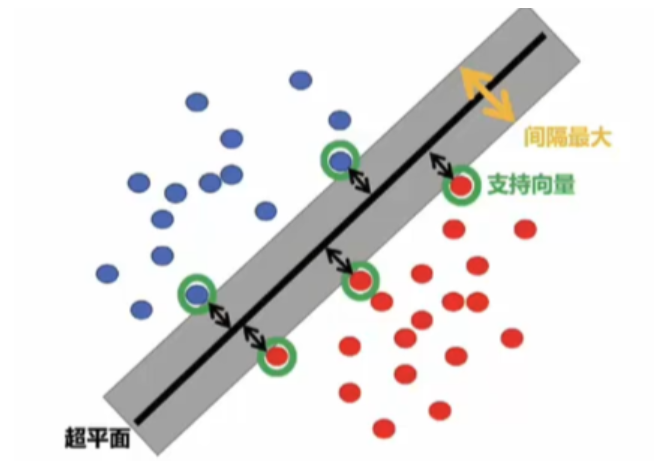
支持向量机（Support Vector Machine，SVM）是一种监督学习算法，主要用于分类和回归任务。其核心思想是通过构造一个最优超平面，最大化不同类别数据之间的间隔。SVM在高维空间中表现优异，尤其适合小样本、非线性及高维数据分类问题。

核心原理

SVM通过寻找一个超平面将数据分隔开，使得不同类别的数据点到超平面的距离最大化。对于线性可分数据，超平面的方程可以表示为： [ w^T x + b = 0 ] 其中 ( w ) 是法向量，( b ) 是偏置项。分类决策函数为： [ f(x) = \text{sign}(w^T x + b) ]

1、超平面方程（优化目标）：分类的基础

SVM 的分类决策依赖于超平面，不同维度空间中的超平面方程具有统一的表达形式：

对于二维平面：

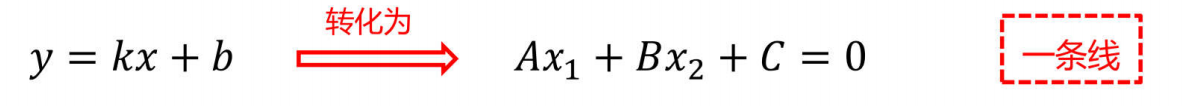
对于三维平面：

对于更高维平面（超平面）：

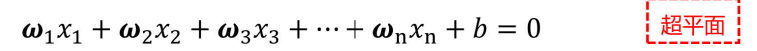
以上可以综合为（超平面函数）：

2、标签与决策函数：严格的分类规则

SVM 中采用 + 1 和 - 1 作为分类标签（而非 0 和 1），这样能让分类规则更严格。

假设超平面能正确分类训练样本，那么：

• 正例（\(y=+1\)）满足\(\omega^t\Phi(x) + b \geq 1\)
• 负例（\(y=-1\)）满足\(\omega^t\Phi(x) + b \leq -1\)

决策函数为：

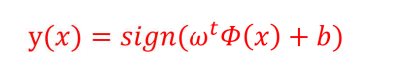
符号函数：

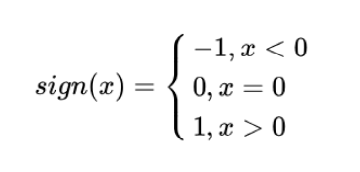
整合在一起就是：

3、距离度量：最大间隔的关键

SVM 追求 "最大间隔"，而间隔的大小由样本点到超平面的距离决定。

点到直线的距离：

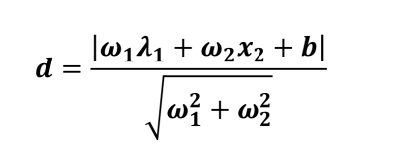
点到平面的距离：

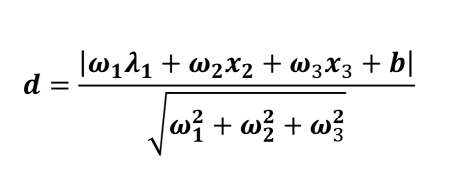
点到超平面的距离：

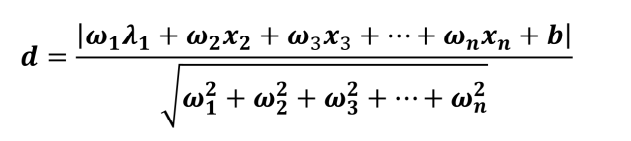
可以简写为：

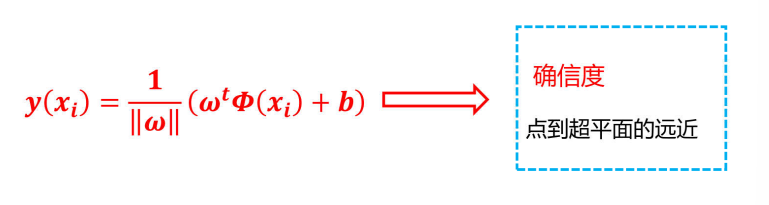
改进：

4、优化求解

如何寻找最优的超平面？

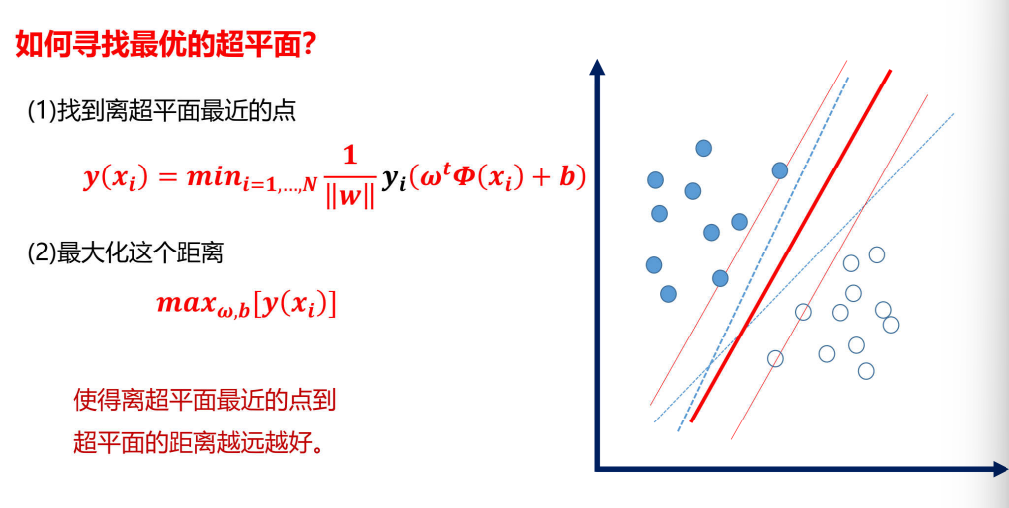
损失函数求解：

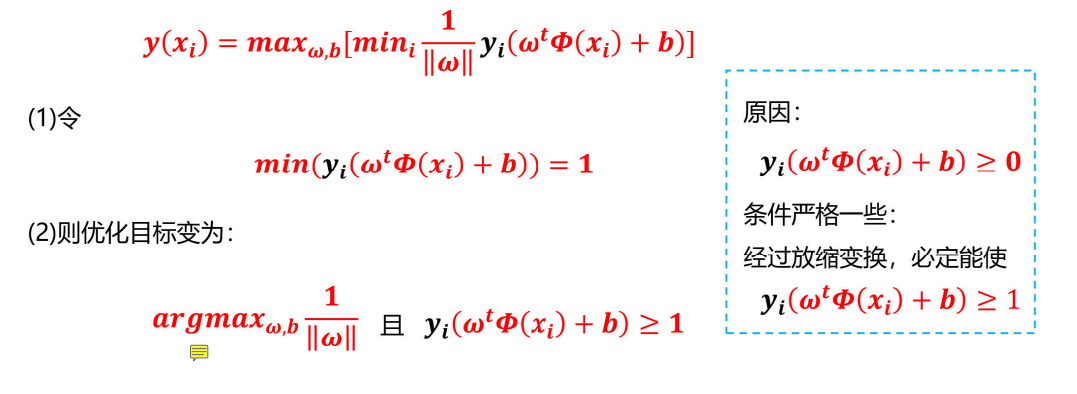
超平面可视化：

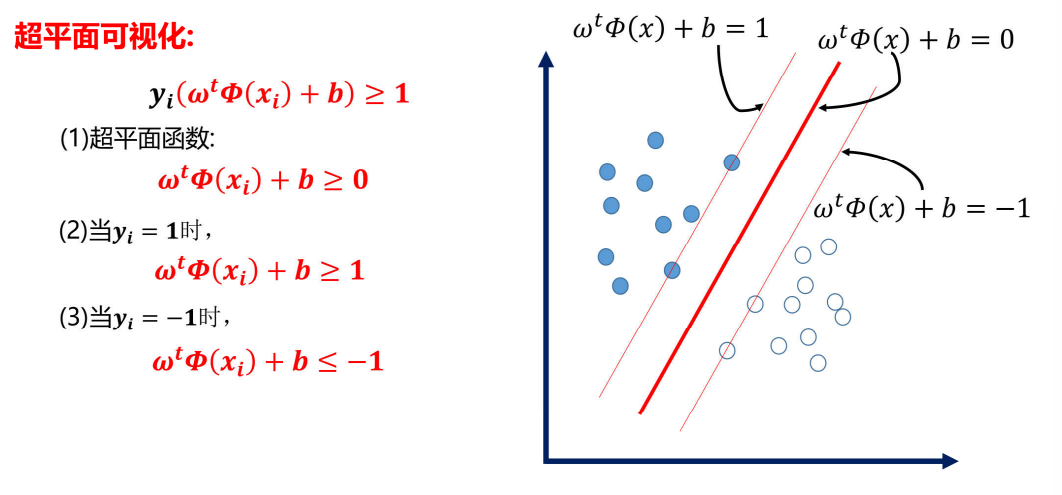
拉格朗日乘子法

整合函数与约束条件：

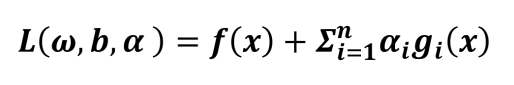
5、支持向量：关键样本的力量

在求解结果中，大部分\(\alpha_i = 0\)，只有少数样本对应的\(\alpha_i > 0\)，这些样本就是 "支持向量"。它们是距离超平面最近的样本，也是决定超平面位置的关键。无论训练样本数量多少，SVM 的最终决策函数仅由支持向量决定，这使得 SVM 的计算复杂度不依赖于样本空间的维数，有效避免了 "维数灾难"。

简单来说：无论数据再多，真正发挥作用的点，是哪些α不等于0的点，就是支持向量

软间隔：

数据中存在一些噪音点，如果考虑这些噪音点的话，超平面可能表现的效果不好

解决：允许个别样本点出现在间隔带里面

量化指标：引入松弛因子

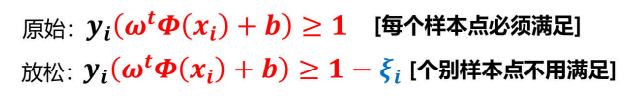
新的目标函数：

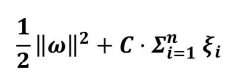
C：惩罚因子

当C值较大时，说明分类比较严格，不容有误

当C值较小时，说明分类比较宽松。可以有误

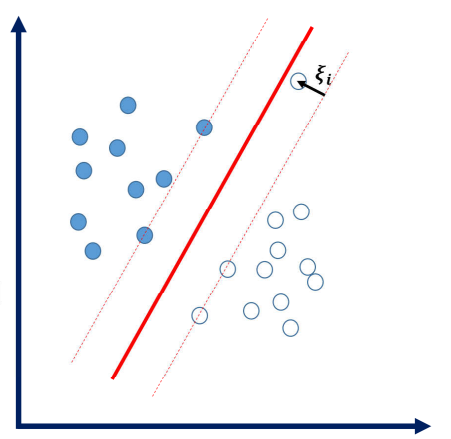
实际数据中往往存在噪音点，如果严格要求所有样本都满足可能导致超平面泛化能力下降。

核函数：解决非线性问题

很多实际问题无法通过线性超平面分离，此时需要将低维数据映射到高维特征空间，使数据在高维空间中线性可分。但直接映射会导致计算复杂度急剧增加，核函数的出现完美解决了这一问题。

核函数的本质是：无需显式进行高维映射，直接在低维空间计算高维空间中样本的内积。即\(K(x_i,x_j) = \Phi(x_i)\cdot\Phi(x_j)\)，这样既实现了高维映射的效果，又避免了高维计算的繁琐。

常用的核函数有三种：

线性核函数、多项式核函数、高斯核函数

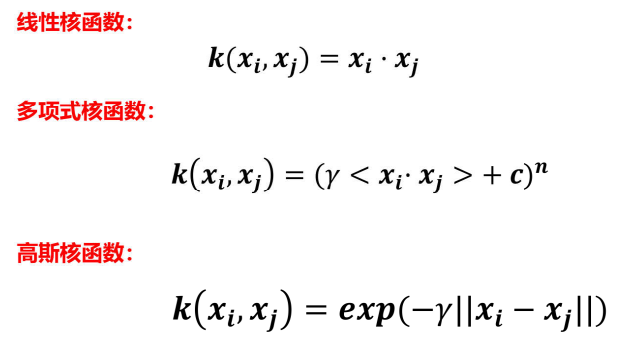
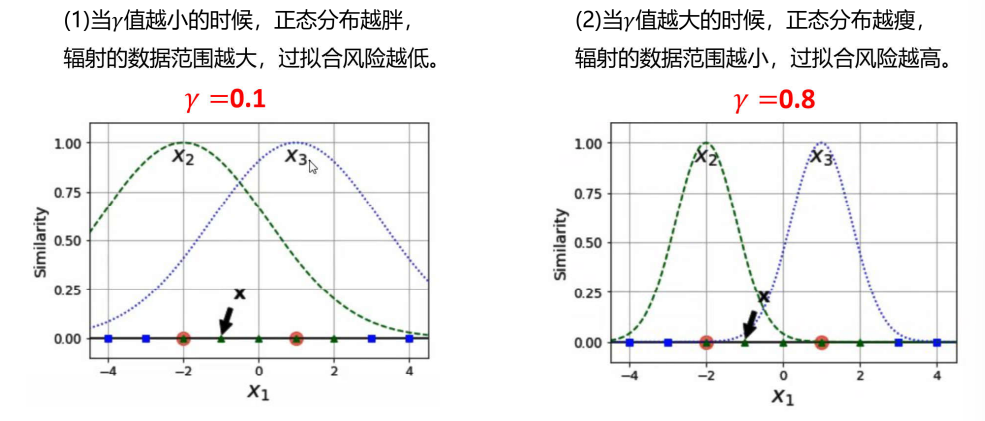
以高斯核函数为例，\(\gamma\)值决定了核函数的 "辐射范围"：\(\gamma\)越小，辐射范围越大，过拟合风险越低；\(\gamma\)越大，辐射范围越小，模型对局部数据越敏感，过拟合风险越高。

γ值

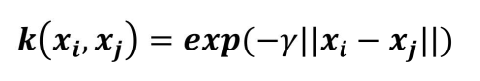
多分类问题

SVM本质上是二分类算法，但可以通过以下方法扩展到多分类：

• 一对一（One-vs-One）：为每对类别训练一个分类器，投票决定最终类别。
• 一对多（One-vs-Rest）：为每个类别训练一个分类器，判断是否属于该类别。

优缺点

优点：

1. 有严格的数学理论支持，可解释性强，不同于传统的统计方法能简化我们遇到的问题。

2. 能找出对任务有关键影响的样本，即支持向量。

3. 软间隔可以有效松弛目标函数。

4. 核函数可以有效解决非线性问题。

5. 最终决策函数只由少数的支持向量所确定，计算的复杂性取决于支持向量的数目，而不是样本空间的维数，这在某种意义上避免了"维数灾难"。

6. SVM在小样本训练集上能够得到比其它算法好很多的结果。

缺点：

1. 对大规模训练样本难以实施。

SVM的空间消耗主要是存储训练样本和核矩阵，当样本数目很大时该矩阵的存储和计算将耗费大量的机器内存和运算时间。超过十万及以上不建议使用SVM。

2. 对参数和核函数选择敏感。

支持向量机性能的优劣主要取决于核函数的选取，所以对于一个实际问题而言，如何根据实际的数据模型选择合适的核函数从而构造SVM算法。目前没有好的解决方法解决核函数的选择问题。

3. 模型预测时，预测时间与支持向量的个数成正比。当支持向量的数量较大时，预测计算复杂度较高。

应用场景

SVM 适用于小样本、高维、非线性的分类任务，例如：文本分类、图像识别、生物信息学中的基因分类、手写体识别等。在这些场景中，SVM 能凭借其泛化能力强、分类精准的优势，取得出色的效果。

支持向量积的API介绍

class sklearn.svm.SVC (C=1.0 , kernel='rbf' , degree=3 , gamma='auto_deprecated' , coef0=0.0 , shrinking=True , probability=False , tol=0.001 , cache_size=200 , class_weight=None , verbose=False , max_iter=-1 , decision_function_shape='ovr' , random_state=None )[source]

1.C ****：****惩罚因子【浮点数，默认为1.】【软间隔】

(1)C越大，对误分类的惩罚增大，希望松弛变量接近0，趋向于对训练集全分对的情况，这样对训练集测试时准确率很高，但泛化能力弱；

(2)C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。

->>建议通过交叉验证来选择

2. kernel : 核函数【默认rbf(径向基核函数|高斯核函数)】

可以选择线性(linear)、多项式(poly)、sigmoid

->>多数情况下选择rbf

3 .degree:【整型，默认3维】

多项式poly函数的维度，默认是3，选择其他核函数时会被忽略。

->>按默认【选择rbf之后，此参数不起作用】

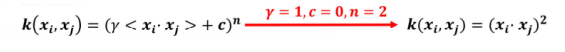
指上面式子中的n

4 . gamma : 'rbf','poly' 和'sigmoid'的核函数参数。默认是'auto'。

(1)如果gamma是'auto'，那么实际系数是1 / n_features，也就是数据如果有10个特征，那么gamma值维0.1。(sklearn0.21版本)

(2)在sklearn0.22版本中，默认为'scale',此时gamma=1 / (n_features*X.var())#X.var()数据集所有值的方差。

<1>gamma越大，过拟合风险越高

<2> gamma越小，过拟合风险越低

->>建议通过交叉验证来选择

****5.coef0:****核函数中的独立项。多项式的偏置项。它只在'poly'和'sigmoid'中很重要。

6. probability：是否启用概率估计。允许在模型训练完成后，使用predict_proba方法来预测每个类别的概率，而不是仅仅给出类别的预测结果。必须在调用fit之前启用它，并且会减慢该方法的速度。默认为False

->>按默认即可【选择rbf之后，不起作用】

7 .cache_size：核函数cache缓存大小，默认为200MB

->>不用调整

8 .class_weight：类别的权重，字典形式传递。默认'balanced'

->>按默认设置

重要的参数有：C、kernel、degree、gamma。

一些属性信息：

1. support_vectors_ 【支持向量】

->>以数组的形式储存

2.n_support_ 【每个类别支持向量的个数】

->>int类型

3.coef_ 【参数w】

->>数组的形式储存

4.intercept_ 【偏置项参数b】

->>数组的形式储存

实例

import pandas as pd
from sklearn.model_selection import train_test_split, cross_val_score

def cm_plot(y, yp):
    """绘制混淆矩阵"""
    from sklearn.metrics import confusion_matrix
    import matplotlib.pyplot as plt

    cm = confusion_matrix(y, yp)
    plt.matshow(cm, cmap=plt.cm.Blues)  # 绘制混淆矩阵
    plt.colorbar()  # 颜色条

    # 在矩阵中标记数值
    for x in range(len(cm)):
        for y in range(len(cm)):
            plt.text(x, y, cm[x, y], ha='center', va='center')

    plt.xlabel('预测值')
    plt.ylabel('真实值')
    plt.title('混淆矩阵')
    plt.show()
data = pd.read_csv(r"E:\xwechat_files\wxid_qi43v1w2nqcb12_e432\msg\file\2025-12\spambase.csv")
X = data.iloc[:, :-1]
y = data.iloc[:, -1]

train_x, test_x, train_y, test_y = train_test_split(X, y, test_size=0.3, random_state=100)

from sklearn.svm import SVC
from sklearn import metrics

svm = SVC(kernel='linear', C=2.0, random_state=0)
svm.fit(train_x, train_y)
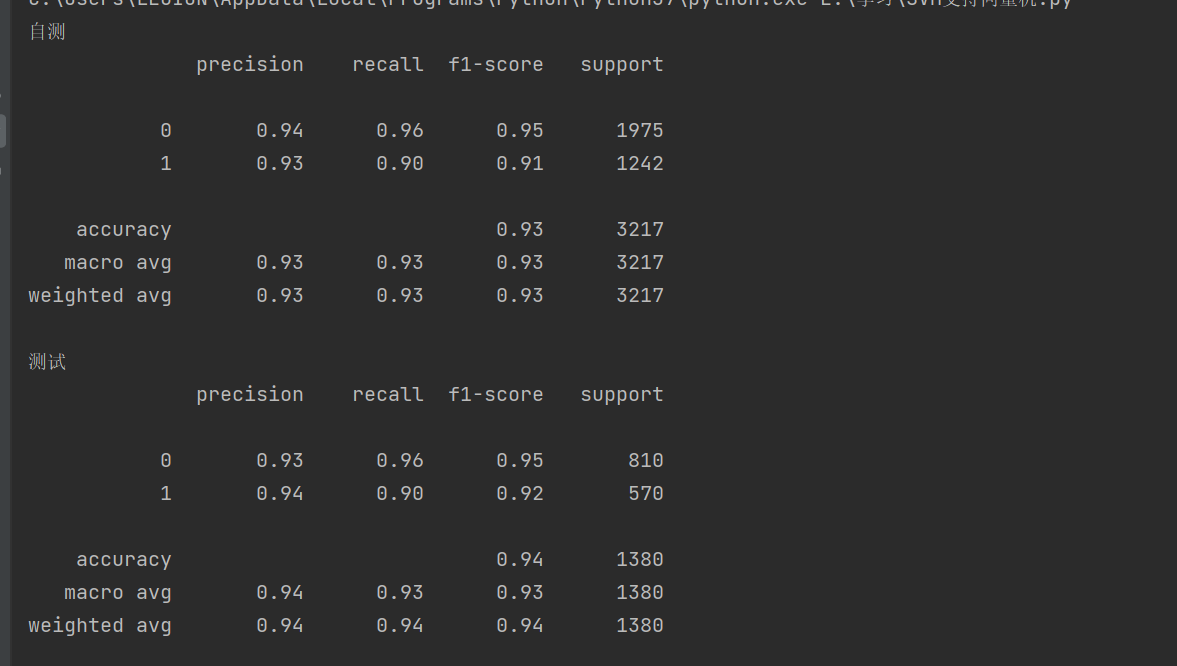
print('自测')
self_predicted = svm.predict(train_x)
print(metrics.classification_report(train_y, self_predicted))
print('测试')
test_predicted = svm.predict(test_x)
print(metrics.classification_report(test_y, test_predicted))

运行结果：