【信号处理MATLAB例程】小波变换执行边缘检测、突变点识别和去噪功能。附代码下载链接

通过小波变换实现了信号的去噪、边缘检测和突变点识别，能够在噪声较大的信号中提取出有意义的信息，适用于信号处理的各种场景。
原创代码，非AI生成，请勿翻卖

文章目录

程序介绍
主要功能模块
运行结果
MATLAB源代码

程序介绍

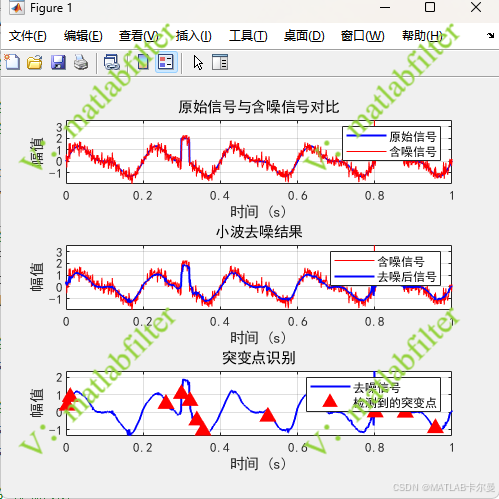
该代码为小波变换下的信号处理与突变点检测的完整流程，包含信号生成、噪声添加、去噪、小波变换、边缘检测和突变点识别。主要包括以下几个步骤：

信号生成与噪声添加：
- 创建一个带有正弦波和方波组成的干净信号。
- 在特定位置（ 300 到 320 及 800 点 300到320及800点 300到320及800点）人为添加突变。
- 随机噪声（高斯噪声）添加到信号中，形成含噪信号。
小波去噪：
- 使用Daubechies 4小波（db4）对含噪信号进行小波分解。
- 利用软阈值法去噪，设定阈值为分解系数的最大值的0.07倍。
- 将去噪后的信号通过小波重构得到去噪信号。
边缘检测：
- 采用连续小波变换（ C W T CWT CWT）来检测信号的边缘，使用高斯一阶导数小波（gaus1）进行变换。
- 计算小波变换系数的模极大值，作为边缘的强度指标。
- 根据预设的阈值（边缘强度的一半最大值），识别信号中的边缘。
突变点识别：
- 使用小波细节系数（高频部分）进行突变点识别。
- 通过提取第一层和第二层细节系数来分析信号中的突变。
- 对于突变的检测，通过找到局部极大值并根据标准差设定阈值来识别突变点。
结果可视化：
- 绘制三幅图：原始信号与噪声信号对比、去噪结果、突变点识别结果。
- 小波变换的系数和细节系数的可视化，包括连续小波变换和第一层小波细节系数。
性能评估：
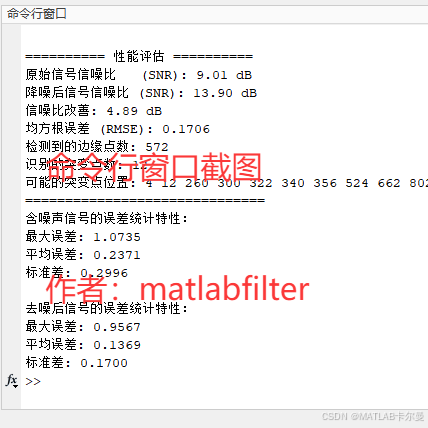
- 计算信号去噪前后的信噪比（SNR），并评估信噪比的改善。
- 计算均方误差（MSE）和均方根误差（RMSE）以评估去噪效果。
- 输出检测到的边缘点和识别的突变点的数量和位置。
误差分析：
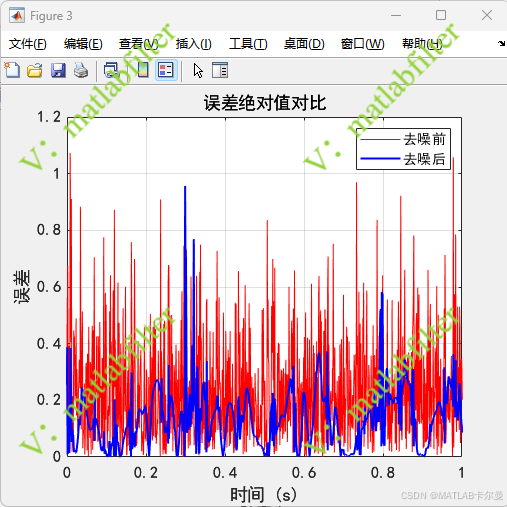
- 计算含噪声信号和去噪信号的误差，并显示误差的统计特性（最大误差、平均误差、标准差）。
- 绘制误差绝对值随时间变化的曲线。

主要功能模块

信号生成与噪声处理：模拟信号的生成和噪声添加，创建含噪声信号。
小波去噪：通过小波变换去除信号中的噪声，保留重要特征。
边缘检测：利用小波变换检测信号中的边缘，应用于信号变化的检测。
突变点识别：基于小波细节系数的分析，识别信号中的突变或突变点。
性能评估：通过信噪比和误差评估去噪效果，并输出评估结果。
误差分析：分析去噪前后信号的误差，评估去噪方法的有效性。

运行结果

信号真值（原始信号）、滤波前后信号、检测到的突变点绘图：

误差绘图：

命令行输出的结果：

MATLAB源代码

部分代码如下：

matlab 复制代码

% 小波变换信号处理，边缘检测、突变点识别、信号去噪

% 作者:matlabfilter（V同号，可接代码定制、讲解与调试）
% 2025-12-21/Ver1

clc;clear;close all;
rng(0);

%% 生成测试信号
fs = 1000;                          % 采样频率
t = 0:1/fs:1;                       % 时间向量
N = length(t);

% 创建复合信号：正弦波 + 方波（突变） + 噪声
signal_clean = sin(2*pi*5*t) + 0.5*sin(2*pi*10*t);

% 添加突变点
signal_clean(300:320) = signal_clean(300:320) + 2;
signal_clean(800) = signal_clean(800) + 3;  % 尖峰

完整代码：
https://download.csdn.net/download/callmeup/92511267

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者