数据结构——通用树（N叉树）

通用树（N叉树）

一、通用树（N叉树）
- 1.1、通用树的表示
- 1.2、Java实现
二、通用树相关问题

一、通用树（N叉树）

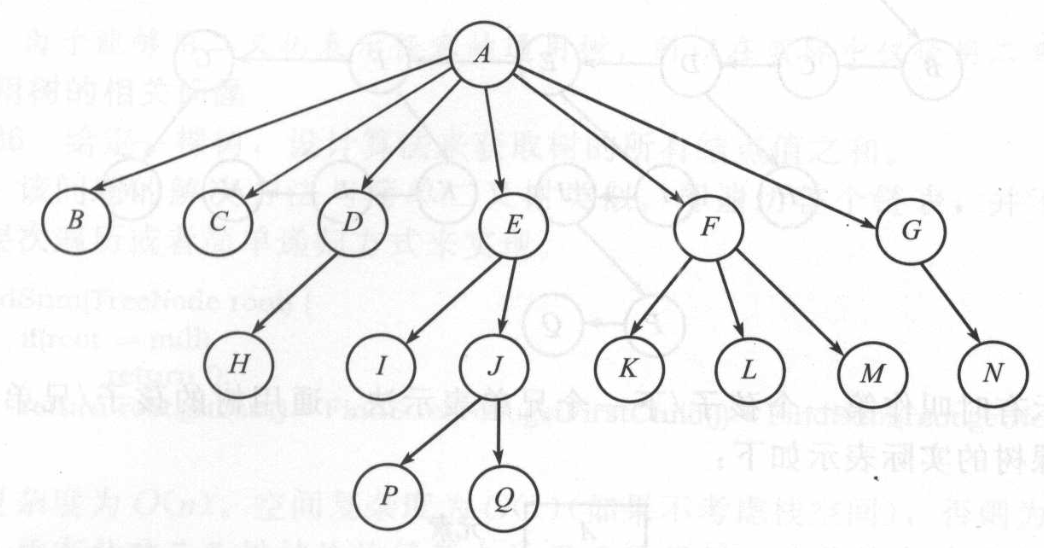
1.1、通用树的表示

同一个双亲结点（兄弟）的孩子结点从左至右排列。
双亲结点只指向第一个孩子结点，删除从双亲结点到其他孩子结点的链接。

上述的具体含义是，如果孩子结点之间有一条链路相连，那么双亲结点就不需要额外的指针指向所有的孩子结点。这是因为从双亲结点的第一个孩子结点开始就能够遍历所有的元素。因此，只要双亲结点用一个指针指向其第一个孩子结点，且同一个双亲结点的所有孩子结点之间都有链路，那么就能解决上面的问题。

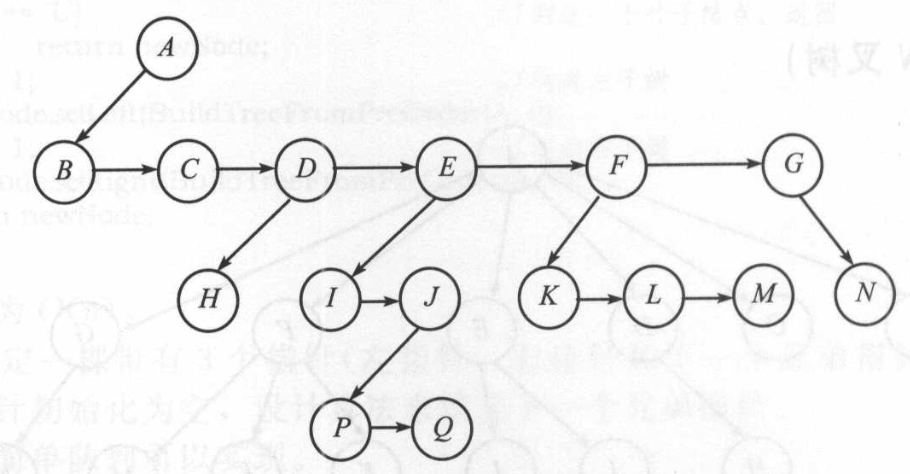
这种表示有时叫作第一个孩子/下一个兄弟表示法。通用树的孩子/兄弟表示法如上图所示。这棵树的实际表示如下：

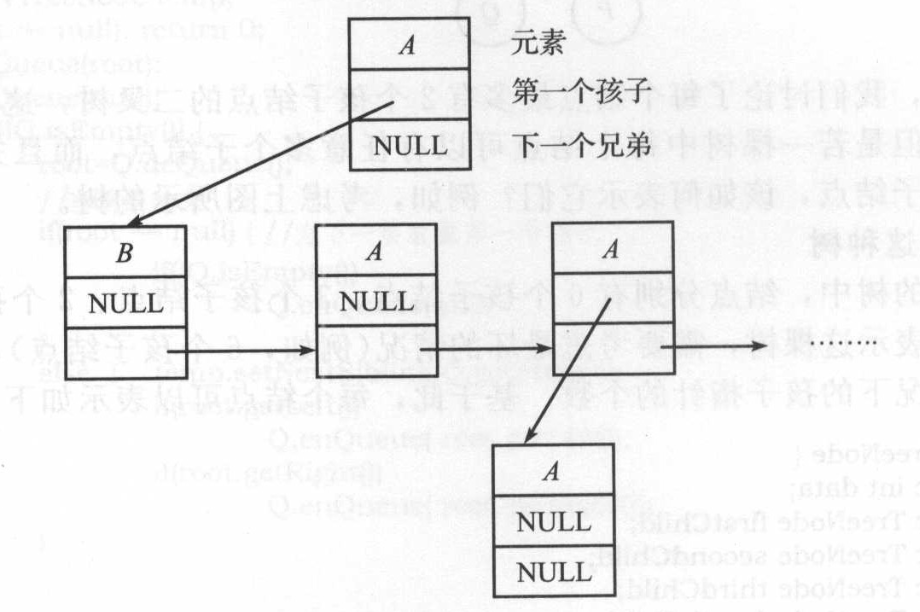
1.2、Java实现

java 复制代码

public class TreeNode {
    public int data;
    public TreeNode firstChild;
    public TreeNode nextSibling;

    public TreeNode() {
    }

    public TreeNode(int data) {
        this.data = data;
    }
}

public class Tree {
    
    private TreeNode root;

    public Tree() {
    }

    public Tree(TreeNode root) {
        this.root = root;
    }

    public TreeNode getRoot() {
        return root;
    }

    public void setRoot(TreeNode root) {
        this.root = root;
    }
}

二、通用树相关问题

2.1、求通用树所有节点值之和

该问题的解决方法与简单二叉树类似。即遍历整个链表，并不断累加其值。可以使用层次遍历或者简单递归方式来实现。

时间复杂度为O(n)，空间复杂度为O(1)如果不考虑栈空间，否则为O(n)。

java 复制代码

/**
 * 求通用树节点之和
 * @param root
 * @return
 */
public int findSum(TreeNode root) {
    if (root == null)
        return 0;
    return root.data + findSum(root.firstChild) + findSum(root.nextSibling);
}

2.2、给定一个双亲节点数组，求树高度

给定一个双亲结点数组P,其中P[门是树的第个结点的双亲结点（假设根结点的双亲结点用一1表示)。设计算法获取树的高度或深度。

根据问题的定义，给定数组表示双亲结点数组。这意味着，需要考察数组对应的树，从而求出树的高度。

例如，如果数组P为：

其对应的树就是：

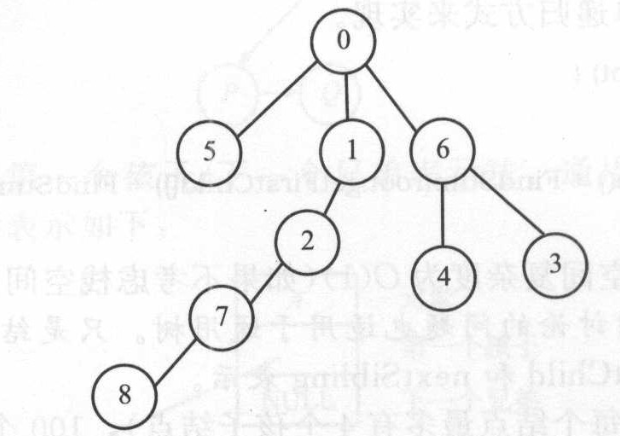
这棵给定树的深度为4。如果仔细观察可得，只需要从每一个结点开始，跟踪找其双亲结点直到找到一1为止，同时跟踪所有结点深度的最大值，就可以得到问题的解。

时间复杂度为O(n²)，对于斜树，将重复计算出与i相同的值。空间复杂度为O(1)。

java 复制代码

/**
 * 给定一个双亲节点数组，求树高度
 * @param p
 * @param n
 * @return
 */
public int findDepthInGenericTree(int[] p, int n) {
    int maxDepth = -1, currentDepth = -1, j;
    for (int i = 0; i < n; i++) {
        currentDepth = 0;
        j = i;
        while (p[j] != -1) {
            currentDepth++;
            j = p[j];
        }
        if (currentDepth > maxDepth)
            maxDepth = currentDepth;
    }
    return maxDepth;
}

2.3、给定一个节点，求其兄弟节点个数

对于树中一个给定结点，只需要遍历其所有的兄弟结点即可。

时间复杂度为O(n)，空间复杂度为O(1)。

java 复制代码

/**
 * 兄弟节点个数
 * @param current
 * @return
 */
public int siblingsCount(TreeNode current) {
    int count = 0;
    while (current != null) {
        count++;
        current = current.nextSibling;
    }
    return count;
}