提示:本文非常长且细腻, 可能是最详细的 pi0 fast学习 笔记, 首先要提前理解 flow matching
文章目录
- 前言
-
- [1 pi0 和 pi0-fast 提升了 什么](#1 pi0 和 pi0-fast 提升了 什么)
- [1.1 整体对比](#1.1 整体对比)
- [1.2 为什么之前的不行: IV 章节:案例研究:动作 tokenization 如何影响 VLA 训练](#1.2 为什么之前的不行: IV 章节:案例研究:动作 tokenization 如何影响 VLA 训练)
- [1.3 为什么FAST 可以?: V 章节: 通过时间序列压缩实现高效动作 Tokenization](#1.3 为什么FAST 可以?: V 章节: 通过时间序列压缩实现高效动作 Tokenization)
-
- [1. 3.1 V-A](#1. 3.1 V-A)
- [1. 3.2 V-B FAST 动作 Tokenization 算法](#1. 3.2 V-B FAST 动作 Tokenization 算法)
-
- [1. 3.2.1 分位数归一化](#1. 3.2.1 分位数归一化)
- [1.3.2.2 对每个动作维度分别应用 DCT(Per-Dimension DCT)](#1.3.2.2 对每个动作维度分别应用 DCT(Per-Dimension DCT))
- [1.3.2.3 通过缩放并取整来量化 DCT 系数(Quantize DCT coefficients via scale-and-round)](#1.3.2.3 通过缩放并取整来量化 DCT 系数(Quantize DCT coefficients via scale-and-round))
- [1.3.2.4 得到稀疏的 DCT 系数矩阵(Obtain sparse DCT coefficient matrices)](#1.3.2.4 得到稀疏的 DCT 系数矩阵(Obtain sparse DCT coefficient matrices))
- [1.3.2.5 将稀疏矩阵展平成一维整数序列(Flatten the sparse matrices into a 1D integer vector)](#1.3.2.5 将稀疏矩阵展平成一维整数序列(Flatten the sparse matrices into a 1D integer vector))
- [1.3.2.6 采用"低频优先"的展平顺序进行交错排列](#1.3.2.6 采用“低频优先”的展平顺序进行交错排列)
- [1.3.2.7 使用 BPE 对整数序列进行无损压缩](#1.3.2.7 使用 BPE 对整数序列进行无损压缩)
- [1.3.2.8 选BPE的原因](#1.3.2.8 选BPE的原因)
- [1.3.2.9 BPE 算法](#1.3.2.9 BPE 算法)
- [2 modeling_pi0fast V.S pi0](#2 modeling_pi0fast V.S pi0)
- 总结
前言
继上一篇深扣pi0 ,这里 继续 看下 pi0 fast
因为我的工程一直追求实践到机器人上干看论文只有空乏的理论. 我按照惯性一直使用的 lerobot, 我之前用的工程已经没有 pi0 fast, 这里我用之前的工程进行代码和 论文的研读. 代码链接见 https://github.com/MexWayne/mexwayne_lerobot_0605
因为 pi0 代码非常简单,所以不详细说明,只是把思路进行精读取

这里 代码和之前有些变化, 因为当时lerobot 工程代码遍地开花, 笔者选了 seeed 的 lerobot 生态好, 代码结构好.
提示:以下是本篇文章正文内容,下面案例可供参考
1 pi0 和 pi0-fast 提升了 什么
1.1 整体对比
在看配置之前 ,我们先整理下 pi0-fast: frequency-space action sequence tokenization. 看看 和pi0 有什么差别.
摘要这里做了整体概述:

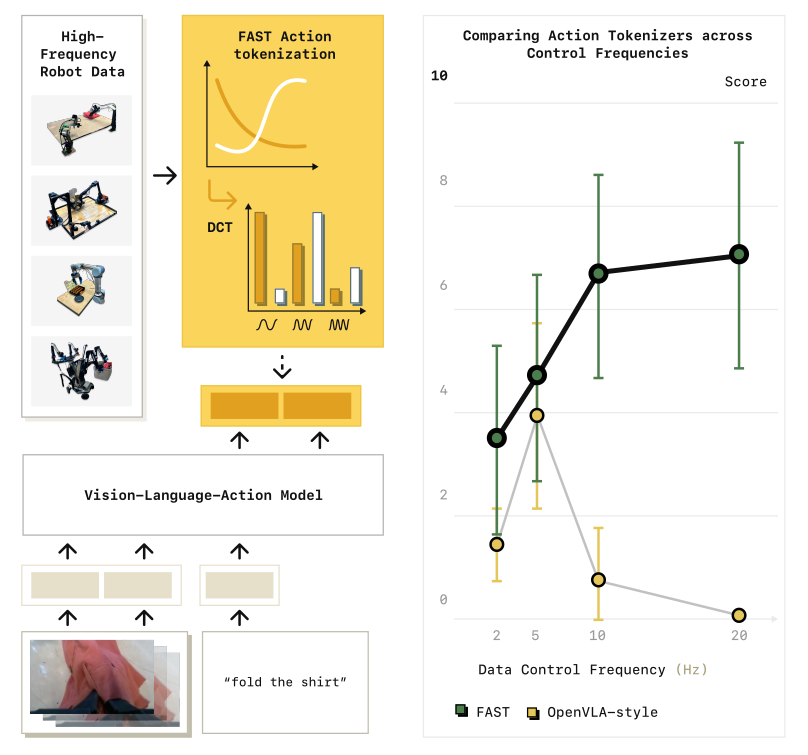
相比 pi0, pi0fast 不是进行专门的提升, 而是让 pi0 在 文章中说"自回归(auto regressive) 处理操作频度高的事情是不可能"的这个问题, 从不可行的事情变得可行,如下图

| 维度 | π0 | π0-FAST |
|---|---|---|
| 动作表示 | 连续 | 离散 token |
| 训练目标 | MSE(flow) | CE(next-token) |
| 生成方式 | Diffusion / ODE | Autoregressive |
| 高频数据 | 天然稳定 | 需要 FAST 才稳定 |
| 训练成本 | 高 | 显著降低 |
| 推理速度 | 快 | 更慢 |
| 工程复杂度 | 数学复杂 | tokenizer + decode 复杂 |
1.2 为什么之前的不行: IV 章节:案例研究:动作 tokenization 如何影响 VLA 训练
本章节 解释了 :为什么之前不行, 指明在 FAST 之前,自回归动作建模在高频控制上是"结构性不可行"的。
原文是这么分析:

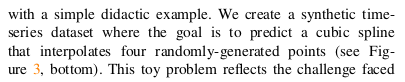
为了说明当前动作 tokenization 方法在训练自回归策略(autoregressive policies)时所面临的挑战,我们从一个简单的教学性案例(didactic example 开始。
我们构造了一个合成时间序列数据集(synthetic time-series dataset) ,其任务目标是:
在给定四个随机生成点(four randomly-generated points)的条件下,预测一条三次样条曲线(cubic spline),使其通过这些点(见图 3 底部)。

这个玩具问题(toy problem)反映了在高频动作块(high-frequency action chunks)场景下训练策略时所面临的挑战:
模型需要在给定条件信息(conditioning information)的情况下,预测一段连续动作序列(sequence of continuous actions)。

使用朴素ization的实验设置
我们首先使用朴素 tokenization 方法(naïve tokenization scheme)对目标信号进行离散化,该方法正是此前多种 VLA 策略所采用的方式。
该方法的策略是:
独立地将其数值离散为 256 个 bin 中的一个
(参见第 III 节)
随后,我们训练一个小型自回归 Transformer 模型(small autoregressive transformer model),在给定条件点的情况下预测这些 token 化后的信号。

采样频率的变化实验
我们在不改变底层数据分布(underlying data distribution)的前提下,重复上述实验,并逐步改变目标信号的采样频率(sampling rate):
(1)从 25 timesteps
(2)到 800 timesteps
(3)每条序列
这相当于在模拟:在不同控制频率(control frequencies)下训练自回归策略。

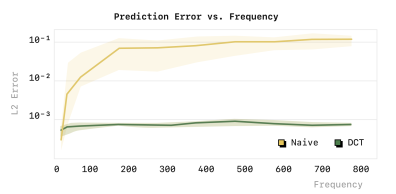
实验结果:高频下训练失败
不同采样频率下模型的平均预测均方误差(average prediction MSE 如图 3 顶部(标注为 "naive")所示。
我们观察到:
在
低采样频率(low sampling rates)下,使用朴素 tokenization 的模型能够取得较好的预测性能(低 MSE)但随着
采样频率的提高,预测误差急剧上升最终,模型退化为简单地复制第一个动作(simply copies the first action)
这一失败行为在图 3 左下角的定性可视化中清晰可见。
左图可以看到 用了 朴素的 tokenization 拟合的 三次曲线效果很差, 而用了DCT tokenization 就拟合的很准确.

这不是数据本身的问题
需要强调的是:
这种失败不能归因于数据本身(cannot be attributed to the data itself),原因如下:
(1)底层数据分布的复杂度并没有变化
(2)如果模型容量相同、训练步数相同,我们本应期待模型在不同采样频率下具有相近的性能.
那么,问题究竟出在哪里?

关键原因:学习目标中的信息量退化
要理解 tokenization 如何影响学习性能,我们需要回到学习目标本身(the learning objective itself)。
从根本上说:自回归模型(autoregressive models) 的训练目标是:
在给定此前所有 token(T₁:i−1)的条件下预测下一个 token(Tᵢ)因此,其学习信号(learning signal)的强度与以下量成正比:
当前 token 在给定历史 token 条件下所包含的边际信息量
(marginal information content of Tᵢ given T₁:i−1)

>>>高频下的致命问题 也是 高频问题的本质问题, 非常重要:边际信息趋近于零<<<<关键在于:当使用
朴素的逐时间步 tokenization(per-timestep tokenization) 方法时, 随着控制频率的提高(as the control frequency increases),在**平滑信号(smooth signals)**的情况下:时间步长变短
单步动作变化量按比例减小
结果是:
每个 token 的边际信息量(marginal information)趋近于零这会显著减慢训练过程中的收敛速度(rate of convergence),
并使得在复杂、高频数据集上进行拟合变得极其困难。
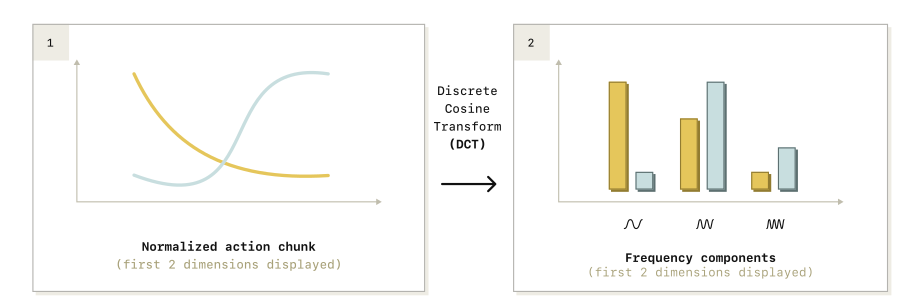
什么是"每个 token 的边际信息量(marginal information)趋近于零"?
marginal information 就是:在已经知道前面所有 token(T₁:i−1)的情况下,当前这个 token(Tᵢ)还能"额外提供多少新信息", 如下图

理解:
论文里的假设:动作轨迹是 平滑的(smooth signals)控制频率很高(例如 50Hz、100Hz)的情况下: a_t ≈ a_{t+1} ≈ a_{t+2} ≈ ...
所以token(Tᵢ)就没多少可学习的内容. 好比做 NLP, 有字符串"哈哈哈哈哈哈哈".
让模型预测下一个字, 模型肯定能预测出来 哈, loss 接近0, 训练也很成功,但是模型什么都没学到.
所以你说
不是模型不够大?
不是数据不够多?
不是优化没调好?
而是:目标函数本身在这个 regime 下"塌缩"了

与已有工作的一致观察
事实上,这种挑战在此前的工作中已有观察:
例如,OpenVLA 在低频数据集(如 BridgeV2、RT-1)上表现良好
但在更高频的 DROID 数据集 上却难以拟合

本案例研究的结论本案例研究的结果清楚地表明:
为机器人动作设计更好的 tokenization 方案(better tokenization schemes)是至关重要的.否则,即便使用强大的自回归 Transformer,在高频控制场景下也会由于学习目标的信息退化(information collapse) 而失败。
1.3 为什么FAST 可以?: V 章节: 通过时间序列压缩实现高效动作 Tokenization


在上一节(IV)里,我们看到:高频动作轨迹(high-frequency action trajectories)里存在
大量冗余(redundancy),会让每个动作 token 的边际信息量(marginal information)变得很低,从而导致训练表现差(poor training performance)。为了解决这个问题,需要一种 tokenization 方法:把高度冗余的动作信号(highly redundant action signal)压缩(compress)成更少但信息量更高的 token(high-information tokens)。接下来作者的安排是:先介绍一种简单的连续时间序列压缩方法(compressing continuous time series)(V-A),再用它设计动作 tokenization 算法(action tokenization algorithm)(V-B),最后说明如何训练一个通用动作 tokenizer(universal tokenizer)(V-C)。
1. 3.1 V-A

V-A. 通过离散余弦变换进行时间序列压缩
我们注意到,对连续时间序列(continuous time series)进行压缩(compression)的方法有很多,包括基于频域变换(frequency-domain transforms)的方法,以及基于学习的压缩方法(learned compression),例如向量量化(vector quantization)。
我们发现,
只要压缩本身足够有效,其具体形式并不是关键;关键在于能否显著降低时间维度上的冗余,从而提升学习效率。在本文中,我们选择使用离散余弦变换(Discrete Cosine Transform, DCT) 作为时间序列压缩方法。DCT 是一种频域表示(frequency-space representation),它将时间信号表示为不同频率余弦函数的线性组合(linear combination of cosine basis functions)。其中,
低频分量(low-frequency components)主要刻画信号的整体形状(overall shape),而高频分量(high-frequency components)更多对应快速变化或噪声(rapid variations or noise)。我们选择 DCT 的原因在于:
(1) 其计算简单、高效(simple and computationally efficient)
(2) 对于平滑变化的时间序列具有良好的压缩性质(highly compressible for smooth signals);
(3)它是一种解析方法(analytical approach),无需额外训练压缩模型。
这些特性使得 DCT 非常适合用于高频机器人动作序列的压缩。
1. 3.2 V-B FAST 动作 Tokenization 算法

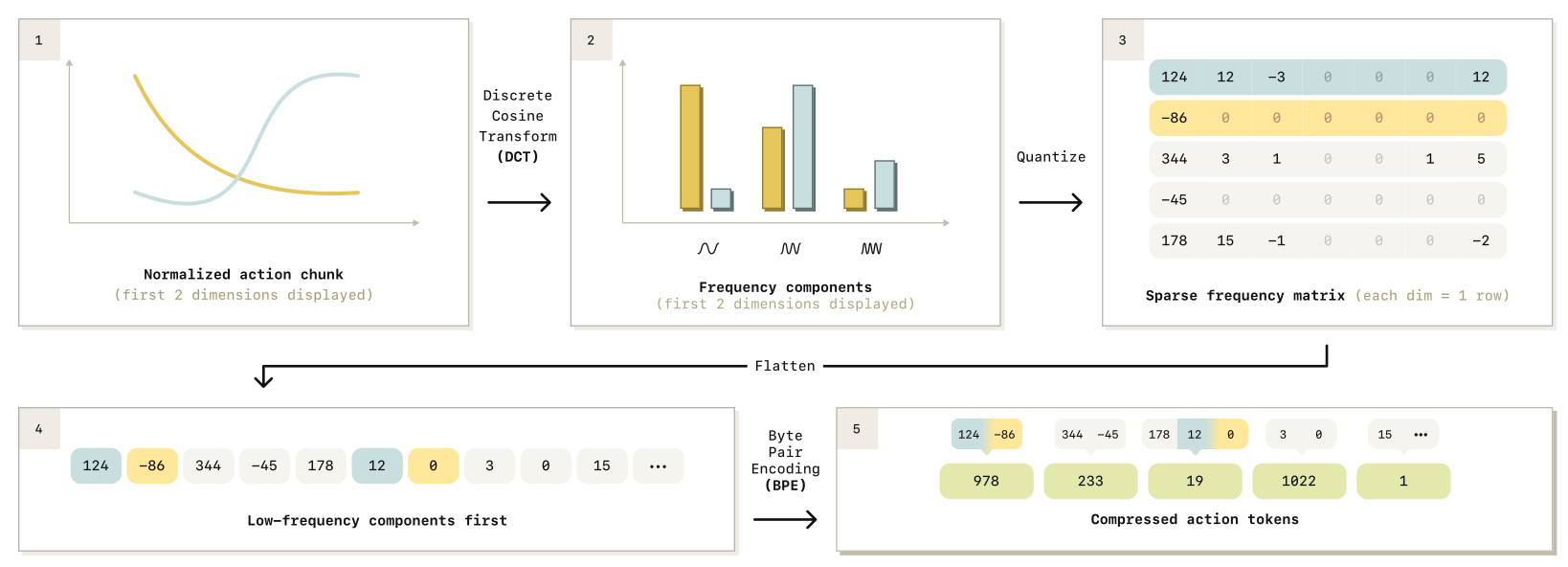
我们借鉴离散cos 变换(DCT) 设计了 FAST(Frequency-space Action Sequence Tokenization),一种用于机器人动作的快速而高效的 tokenization 算法。FAST 的完整流程如图 4 所示。
下面我们逐步描述从连续动作序列到离散动作 token 的整个处理过程。
1. 3.2.1 分位数归一化

首先,我们对输入动作序列进行归一化(normalize the input actions)。具体而言,我们将训练数据中每个动作维度的 第 1 百分位数(1st quantile)和第 99 百分位数(99th quantile) 映射到区间
−1,1\]。 我们采用分位数而非最小值/最大值的原因是:这种做法对异常值(outliers)更加鲁棒(robust),并且有助于在跨机器人、跨动作尺度的数据集(cross-embodiment datasets with different action scales)之间共享 tokenizer。而且这种情况在我们的数据集中时不时会发生.
1.3.2.2 对每个动作维度分别应用 DCT(Per-Dimension DCT)

在完成归一化之后,我们对每一个动作维度分别应用离散余弦变换(discrete cosine transform, DCT)。
1.3.2.3 通过缩放并取整来量化 DCT 系数(Quantize DCT coefficients via scale-and-round)

为了压缩 DCT 变换后的信号,我们本可以直接省略不重要的系数(omit insignificant coefficients);但在实现中,我们采用**缩放并取整(scale-and-round)的操作方式。其中,缩放系数(scaling coefficient)是一个超参数(hyperparameter),用于在压缩过程的有损性(lossiness)与压缩率(compression rate)**之间进行权衡。
1.3.2.4 得到稀疏的 DCT 系数矩阵(Obtain sparse DCT coefficient matrices)

在取整之后,DCT 系数矩阵通常呈现出稀疏性(sparse):大多数条目为零(most entries being zero),每个动作维度仅保留少量显著系数(a few significant coefficients)。
1.3.2.5 将稀疏矩阵展平成一维整数序列(Flatten the sparse matrices into a 1D integer vector)


为了真正实现压缩效果,我们必须将这一稀疏矩阵转换为一串稠密 token。为此,我们将该矩阵展平成一个一维整数向量(1-dimensional vector of integers)。
1.3.2.6 采用"低频优先"的展平顺序进行交错排列
(Low-frequency-first interleaving across action dimensions)

在展平过程中,我们通过优先包含所有动作维度的低频分量(including all low-frequency components first),对不同动作维度进行交错排列(interleaving)。
1.3.2.7 使用 BPE 对整数序列进行无损压缩

随后,我们训练一个字节对编码(Byte Pair Encoding, BPE) tokenizer,对展平后的一维整数向量进行无损压缩(losslessly compress),从而得到稠密的动作 tokens。该步骤能够压缩大量零值分量,并合并在不同动作维度之间频繁共现的系数组合。
1.3.2.8 选BPE的原因

实现多,且容易量化 其他也能用.
有个细节 两种编码模式 ,如果是 colmun first, 那么就是将一个动作序列的 所有频段concat 到一起.如果是 row-first 那么就是 生成一个完整动作的序列后,将所有动作concat到一起.
这些步骤就是:

过程也和下图流程图一样
1.3.2.9 BPE 算法
这里 额外说下BPE:
训练算法(经典 BPE):
step1 初始:把序列拆成最小单位(在文本里是字符;在这里可以理解为"基础符号/基础整数 token")
step2 重复以下步骤,直到词表达到设定大小(比如 1024):
step3 统计所有序列里 **相邻 token 对(pairs)**出现次数
step4 找到出现次数最多的一对(most frequent pair)
step5 把它们合并成一个新 token(merge)
step6 在所有序列中用新 token 替换这对相邻 token
step7 更新统计,继续
论里说的 "train" 是因为要从数据统计中学到 哪些相邻组合最常出现、最值得合并。
2 modeling_pi0fast V.S pi0
| 对比项 | π0(modeling_pi0.py) |
π0-fast(modeling_pi0fast.py) |
|---|---|---|
| 训练目标 | Flow matching / diffusion-style :构造 x_t = t·noise + (1-t)·actions,监督目标 u_t = noise - actions,预测 v_t,用 MSE(u_t, v_t) 训练 |
自回归 next-token CE :把 action 变成 tokens 后拼到输入序列里,输出 logits 后 shift 做 CrossEntropyLoss ,并用 loss_mask 只在 action 段计算 |
| 动作表示 | 动作是连续张量(padded 到 max_action_dim),作为 suffix 条件输入给 action expert(action_in_proj / action_out_proj) |
动作被 FAST tokenizer 编码成离散 token ids,并映射到 PaliGemma 词表尾部的一段 token id 区间 |
| 训练输入构造 | prefix:图像+语言;suffix:state + x_t + time(在 embed_suffix 中构造) |
prefix 文本里显式包含:Task: ... , State: <离散化state>;;suffix 是 "Action: " + FAST action tokens + eos |
| 注意力/掩码机制 | 用 2D/4D attention mask 拼 prefix+suffix,让 suffix 能 attend prefix(以及自身的有效部分) | 显式构造 token_type_ids + block-causal mask:不在 prefix 上算 loss,只在 action 段的非 padding 上算 |
| 推理方式 | 迭代去噪(ODE/步进) :num_inference_steps 次循环更新 x_t = x_t + dt·v_t,最终得到动作序列;默认步数 10 |
LM generate :调用 pi0_paligemma.generate(max_new_tokens=...) 生成 action tokens,再 detokenize 成动作;max_decoding_steps=256 |
| 动作解码 | 不需要 tokenizer:去噪结束的 x_t 直接就是动作(连续) |
decode_actions_with_fast():BPE decode → 还原 DCT 系数 → idct 回到时域动作;支持 relaxed padding/truncation |
| chunk / 执行步数(默认 config) | chunk_size=50,n_action_steps=50;推理去噪步数 num_inference_steps=10 |
chunk_size=10,n_action_steps=5 |
| "快"的来源 | 主要成本在 去噪迭代(多次 denoise_step) | 主要成本在 一次 generate + detokenize;没有 diffusion-style 多步去噪循环 |
总结
1 高频操作auto agregraion 训练不好的本质问题: 出 为机器人动作设计更好的 tokenization 方案是至关重要的.
2 时间序列压缩: 实现高校的 动作 tokenization 解决 1 提出的问题
3 融合 frequency action equence tokenization 后可以进行 自回归训练, 段平快, 而且解决了 操作高频的问题