斯坦福大学 | CS336 | 从零开始构建语言模型 | Spring 2025 | 笔记 | Lecture 17: Alignment - RL 2

目录

• • 前言
  • [1. Overview](#1. Overview)
  • [2. RL setup for language models](#2. RL setup for language models)
  • [3. Policy gradient](#3. Policy gradient)
  • • [3.1 Navie policy gradient](#3.1 Navie policy gradient)
    • [3.2 Baselines](#3.2 Baselines)
    • [3.3 Advantage functions](#3.3 Advantage functions)
  • [4. Training walkthrough](#4. Training walkthrough)
  • • [4.1 Simple task](#4.1 Simple task)
    • [4.2 Simple model](#4.2 Simple model)
    • [4.3 Run policy gradient](#4.3 Run policy gradient)
    • [4.4 Experiments](#4.4 Experiments)
  • [5. Summary](#5. Summary)
  • 结语
  • 参考

前言

学习斯坦福的 CS336 课程，本篇文章记录课程第十七讲：对齐 - RL（下），记录下个人学习笔记，仅供自己参考😄

website：https://stanford-cs336.github.io/spring2025

video：https://www.youtube.com/playlist?list=PLoROMvodv4rOY23Y0BoGoBGgQ1zmU_MT_

materials：https://github.com/stanford-cs336/spring2025-lectures

course material：https://stanford-cs336.github.io/spring2025-lectures/?trace=var/traces/lecture_17.json

1. Overview

在开始今天的课程之前先做个简单的说明，这是本系列课程的最后一讲

上节课我们概述了基于可验证奖励的强化学习，并讲解了 PPO、GRPO 等策略梯度算法，本节课我们将深入探讨策略梯度算法 GRPO 的工作机制，我们不会涉及全新知识，而是基于现有知识进行更深入的探讨，同时会展示相关代码和数学推导

2. RL setup for language models

先简单了解一下我们要探讨的内容

我们正在研究语言模型的强化学习，在强化学习中需要明确定义 状态（State, s）、动作（Action, a）和奖励（Rewards, R） 等要素，当前状态由初始提示词（prompt）和已生成的所有响应内容共同构成，每个动作对应生成一个特定的 token，即下一个待生成的 token，奖励值本质上反映了生成响应内容的质量优劣

在本课程中，我们将重点讨论结果奖励，即奖励函数基于完整响应内容进行计算，我们将重点关注可验证的奖励机制，因此整个计算过程是确定性的，某些函数可以直接返回奖励值，而无需人工参与评估，在这种设定下，强化学习通常会涉及折扣因子和自助法（bootstrapping）的概念，这适用于多轮交互场景，即智能体通过连续多轮决策逐步获得奖励，当存在中间过程奖励时，这种机制就显得尤为重要

如果场景更偏向于执行一系列动作后直接验证最终答案的正确性，这显然会带来诸多挑战，此时的奖励信号既稀疏又具有延迟性，但换个角度看，这种设定反而简化了相关的概念性思考。例如，假设现在有一道数学题，接着你会进行一段时间的思维推演，最终，语言模型可能会生成答案："... Therefore, the answer is 3 miles."，随后，奖励机制需要从中提取 "3 miles" 这个结果并核验其是否符合既定标准答案

在强化学习中，研究者通常重点讨论状态转移动态特性 T ( s ′ ∣ s , a ) T \left(s' \mid s, a\right) T(s′∣s,a)，在语言模型的应用场景中，这种状态转移特性反而显得异常简单，这仅仅是简单的加法运算，只需将执行动作直接追加至当前状态即可，也就是 s ′ = s + a s' = s + a s′=s+a，这种机制具有深远影响，由于掌握了环境动态规律，我们能够实现更优控制，这使你能够在测试阶段执行规划计算，这正是机器人专家梦寐以求的能力 -- 若能获得环境的状态转移模型和动态规律，他们就能进行仿真模拟，实现所有这些操作，在语言建模领域我们能够实现这一点，但这在通用强化学习中通常难以达成

另一个关键认知在于：所谓 "状态" 的概念本质上是人为构建的，在机器人领域的强化学习中，所谓 "状态" 可能包含关节角度、位置坐标、视觉图像等要素，这种状态定义确实与现实世界紧密相连，而语言模型中的状态仅仅是模型随机生成的文本 token 序列，这种机制赋予了语言模型极大的灵活性，使其能够通过自主构建思维草稿来逐步推导最终答案

而机器人则往往受限于现实世界的物理约束，其可达到的状态范围存在客观限制，因此问题的核心并非在于状态可达性 -- 这通常是机器人学与控制领域面临的挑战，某些状态在物理层面就根本不可实现，在语言模型中，你只需输出文本 token 就能抵达任意状态，但真正的挑战在于确保这些 token 最终能推导出符合事实的正确答案

这确实值得我们深入思考，这完全属于强化学习的范畴，但其中的难点与易点以及背后的原理认知，在语言建模场景下已发生本质变化

因此在这种情况下，策略 π ( a ∣ s ) \pi \left( a \mid s \right) π(a∣s) 就是一个语言模型，其动作（即生成的内容）取决于当前状态，也就是已有的提示词和已生成的回复内容，这通常是在已有预训练语言模型基础上进行微调的

这种从初始状态到终止状态的完整交互过程，在领域内有多种术语表述，在这种结果奖励的设定下，必须从某个初始状态开始生成一系列动作即 tokens，你将获得一个单一数值即奖励值，也就是 s → a → ⋯ → a → a → R s \to a \to \dots \to a \to a \to R s→a→⋯→a→a→R

而你的目标就是最大化期望奖励值 E [ R ] E[R] E[R]，这里的期望既包含环境给出的提示词（prompts）也包含待优化策略 π \pi π 生成的响应 token，这样就能确保整个框架既扎实又精确

3. Policy gradient

现在我们来探讨策略梯度，这是一整套用于学习策略的方法，其核心思路是从初始策略出发，通过梯度方法逐步优化提升。为简化表示，我们将用 a a a 代表整个响应（response），而不仅指单个动作（action），由于我们处于结果奖励（outcome reward）的设定下，你可以将这些动作理解为由语言模型一次性生成的全部输出，最终你会获得一个综合的奖励值

3.1 Navie policy gradient

请记住，我们的目标是通过优化策略 π \pi π 来最大化预期奖励，因此，预期奖励可表示为：

E [ R ] = ∫ p ( s ) π ( a ∣ s ) R ( s , a ) \mathbb{E}[R] = \int p(s) \pi(a \mid s) R(s, a) E[R]=∫p(s)π(a∣s)R(s,a)

也就是在状态分布 p ( s ) p\left(s\right) p(s) 上积分，乘以给定状态下策略生成动作序列的概率 π ( a ∣ s ) \pi(a \mid s) π(a∣s)，再乘以对应的奖励值 R ( s , a ) R(s, a) R(s,a)，这个表达式相当直观明了

而策略梯度算法采用的正是这种直观思路，让我们对其求梯度，计算过程如下：

∇ E [ R ] = ∫ p ( s ) ∇ π ( a ∣ s ) R ( s , a ) = ∫ p ( s ) π ( a ∣ s ) ∇ log ⁡ π ( a ∣ s ) R ( s , a ) = E [ ∇ log ⁡ π ( a ∣ s ) R ( s , a ) ] \begin{align*} \nabla \mathbb{E}[R] &= \int p(s) \nabla \pi(a \mid s) R(s, a) \\ &= \int p(s) \pi(a \mid s) \nabla \log \pi(a \mid s) R(s, a) \\ &= \mathbb{E}\left[ \nabla \log \pi(a \mid s) R(s, a) \right] \end{align*} ∇E[R]=∫p(s)∇π(a∣s)R(s,a)=∫p(s)π(a∣s)∇logπ(a∣s)R(s,a)=E[∇logπ(a∣s)R(s,a)]

梯度仅作用于策略本身 ，这正是关键技巧所在，这类似于所谓的策略梯度定理，但这本质上只是对数函数的链式法则，因此，这本质上可以重写为 π \pi π 与对数梯度的乘积形式。最后，我们可以用期望值的形式重新表述它，这里的期望值本质上隐含了对 状态 - 动作 - 下一状态 分布的考量，这种形式应该让人感到非常熟悉，这就是期望奖励的梯度的最终形式

朴素策略梯度方法的核心思路是：从提示分布 p p p 中采样一个提示，从动作空间 a a a 中采样一个响应，然后直接根据这个期望内部的表达式 ∇ log ⁡ π ( a ∣ s ) R ( s , a ) \nabla \log \pi(a \mid s) R(s, a) ∇logπ(a∣s)R(s,a) 来更新参数，想象一下，当你在做随机梯度下降时，你只需查看样本项的期望损失，评估后直接使用它进行优化，从本质上说，这种形式与 SGD 如出一辙，只不过每个元素都按奖励值进行了加权处理

当人类专家写下动作 a a a 时，系统只需模仿这个动作 a a a，并通过调整参数来最大化选择该动作的概率，而现在这个动作 a a a 是由模型自主生成的，关键区别在于 -- 现在你可以用奖励值来调控这个动作

为了帮助建立直观理解，假设奖励值只能是 0 或 1 这两种情况，要么正确要么错误，也就是说 R ( s , a ) ∈ { 0 , 1 } R(s, a) \in \{0, 1\} R(s,a)∈{0,1}，在这种情况下，原始策略梯度将仅针对正确响应进行更新，因此对于导致错误响应的动作，奖励值 R R R 将被设为 0，此时这些动作将被完全忽略。而对于正确响应，奖励值 R R R 则为 1，因此本质上你只需采样筛选出正确的响应，然后针对这些响应执行 SGD 操作，唯一的区别在于数据集会随时间变化，因为每次策略更新后，你都会基于新策略重新生成数据集，如此循环迭代，这其实非常自然

策略梯度方面面临的主要挑战在于其噪声大、方差高。在随机梯度下降中，即便进行监督学习时，梯度也可能存在显著噪声，通常只需增大批次规模并持续训练，经验表明这种方法最终都能奏效，而强化学习在噪声和方差处理方面完全是另一个量级的挑战

具体来说，假设你面对的是 0 或 1 二元奖励机制的场景 -- 想象一下解决数学难题的场景，这种稀疏奖励机制意味着只有极少数响应能获得值为 1 的奖励，绝大多数响应得到的奖励都是 0，当策略欠佳时，执行动作产生的奖励绝大多数都会是 0，这意味着观察梯度时，实际上执行的几乎是零梯度更新

那么，如果你的策略差到拿不到任何奖励，结果会怎样？你的梯度更新就会完全停滞，陷入僵局，这种状态显然非常不利，至少在监督学习中，你还能朝着某个明确方向进行更新，但在强化学习和稀疏奖励的场景下，情况就会完全不同了

Q & A

Q：为什么数据集会随时间变化？

A ：问题在于：为什么数据集会随时间动态变化？若我们审视 E [ R ] = ∫ p ( s ) π ( a ∣ s ) R ( s , a ) \mathbb{E}[R] = \int p(s) \pi(a \mid s) R(s, a) E[R]=∫p(s)π(a∣s)R(s,a) 这个目标函数，我们需要对其进行优化，于是我们通过迭代逐步优化，接下来我们将计算梯度并更新参数，梯度计算过程包含：采样响应数据，随后执行参数更新，此时，模型参数已完成更新，下次采样时生成的响应可能会发生变化，由于模型已完成更新，若进行多次响应采样，这些响应数据将来自与初始状态不同的概率分布，随着迭代推进，采样数据集的质量将逐步提升。

直观来看，即便面对稀疏奖励场景，只要模型能正确解答部分简单问题并获得相应奖励，通过持续更新模型参数就有望使模型泛化能力超越这些初始示例，因此在下一轮迭代中，当模型尝试解答难度稍高的问题时，自然会产生部分正确答案的响应样本，如此循环迭代，数据集中的高奖励样本比例将呈现持续上升趋势

这与基于人类反馈的强化学习（RLHF）形成鲜明对比，后者通过成对偏好比较来训练奖励模型，而奖励模型的输出通常具有更强的连续性特征，该模型会为每个生成响应分配具体的数值评分，精确量化其优劣程度，这与可验证奖励机制形成鲜明对比，它仅作二元判定（正确/错误）

请注意，我们之所以反复强调这一点，是因为所有这些方法本质上都属于强化学习的范畴，即便在语言模型的应用框架下，这些方法依然完全遵循强化学习的核心范式，有时甚至会使用相同的算法（如 PPO），但在设计直觉层面 -- 包括超参数设置方式与模型调优策略将存在显著差异

Q & A

Q：我注意到奖励信号具有稀疏性特征，当奖励值为 0 时，系统将保持参数不更新，这种理解是否正确？那么是否应该将其设为 -1，使其反向作用，从而利用这些奖励信号呢？

A：这里的问题在于，当奖励值为 0 时，系统确实不会更新参数，为何不将奖励值设为负值（如 -1）呢，这样至少能推动模型远离那些错误响应。当我们引入基线机制时，这种情况会自动得到处理，这是因为当前使用的只是最基础的策略梯度方法，直接根据奖励值进行参数更新，我们将证明存在比单纯使用奖励值更优的解决方案。

Q：奖励是提示与完整响应的函数，而响应正确与否只有在完整生成后才能判定，那么梯度仅作用于最后一个 token 吗？

A：你的意思是说，有时在生成完全前就能获得奖励，另一种奖励机制称为过程监督或过程奖励，它能实时追踪当前生成质量，这方面确实存在可行的解决方案，通常来说，如果过程奖励设计得当，效果会更好，为简化讨论，这里暂时假设我们仅使用结果奖励，但毫无疑问，若能提前获得可信的奖励信号就应该尽早进行奖励评估。语言模型中使用过程奖励的根本问题在于 -- 在语言模型中构建有效的过程奖励机制存在本质困难，除非模型输出完全偏离轨道，否则很难准确评估其表现优劣。

Q：我们当前使用的奖励模型是什么？这里的 0 和 1 是如何确定的？

A：问题在于：当前的奖励模型具体是什么？我们来展示几个这方面的具体示例，不过可以这样理解奖励模型，根据你们的作业要求，你们要实现的基本流程是：语言模型生成内容后解析出答案，将其与标准答案比对，匹配则返回 1，否则返回 0，因此，为了最大化期望奖励，策略梯度算法采取了最直观的做法 -- 朴素策略梯度，但这种方式存在噪声大、方差高的问题。

3.2 Baselines

策略梯度方法的一个核心思路就是引入所谓的 "基线（baseline）"，我们回想一下，这里讨论的正是期望奖励 ∇ E [ R ] = E  ⁣ [ ∇ log ⁡ π ( a ∣ s )   R ( s , a ) ] \nabla \mathbb{E}[R] = \mathbb{E}\!\left[ \nabla \log \pi(a \mid s)\, R(s, a) \right] ∇E[R]=E[∇logπ(a∣s)R(s,a)]，如果能准确计算出这个期望奖励值，问题就迎刃而解了，因为这样就能直接计算出结果，但现实情况是做不到

因此我们转而采用无偏估计 ∇ log ⁡ π ( a ∣ s )   R ( s , a ) \nabla \log \pi(a \mid s)\, R(s, a) ∇logπ(a∣s)R(s,a)，通常的做法是直接去掉期望符号，通过采样来近似计算，这种估计方法虽然无偏，但方差可能相当大

举个简单的例子就能明白什么是高方差，假设只有两个状态（可以理解为两个提示词）s1 和 s2：

• s1: a1 → reward 11, a2 → reward 9
• s2: a1 → reward 0, a2 → reward 2

在状态 s1 下存在两个可选动作，选择动作 a1 将获得 11 的奖励，选择动作 a2 则获得 9 的奖励，而在状态 s2 下，选择动作 a1 获得 0 奖励，选择动作 a2 则获得 2 奖励。显然，状态 s1 能带来更高的回报，而状态 s2 的回报水平相对较低，显然最优策略应该是：在状态 s1 选择动作 a1，在状态 s2 选择动作 a2

因此，在状态 s1 时，我们应当避免选择动作 a2，但请注意，这里的 9（状态 s1 的奖励）实际上比状态 s2 的奖励更高，这种情况可能导致：当我们将状态 s1 视为一个极其简单的问题时，其高额奖励会形成强烈对比，而状态 s2 可能对应着更困难的问题，因此，仅因某个动作获得高额奖励，并不意味着我们必须激进地调整策略来强化它

采用原始梯度更新方法时，系统可能会错误地选择在状态 s1 执行动作 a2，看起来这似乎是个绝佳选择，这样就能获得 9 倍的梯度更新量，而当我们观察状态 s2 下执行动作 a2 时，发现其奖励值仅为 2，因此我们对这个动作的梯度更新力度较小，但实际上，纵观全局就会发现这种局部最优的选择可能并不合理

需要强调的是，这种情况仅存在于期望值层面，若从整体状态和动作的角度来看，最终结果仍会趋于平衡，数学推导最终是自洽的，但必须通盘考量才能得出这个结论

Q & A

Q：为何在第一种情况下要使用 a2？

A：问题在于：为何要选择 a2？所以最终选择哪个动作，完全取决于策略函数的决策，在策略初始阶段，你并不知道哪个动作能获得更高奖励，所以一开始可能会随机选择动作，恰好选择了动作 a2，就可能会强化这个选择并获得 9 分的奖励。但问题其实更严重 -- 当你看到 "哇，9 分奖励，这简直太棒了" 时，你越是频繁选择这个动作，就会不断强化这个选择，最终就会陷入这个局部最优的困境，连其他选择的机会都没有了，由于过度强化 a2 的更新，导致 a1 的选择概率已经完全消失了。

基线方法的核心思想在于：我们只需最大化基线奖励即可，我们不再直接优化期望奖励，而是引入一个称为基线函数 b ( s ) b\left(s\right) b(s)，用实际奖励减去这个基线值，也就是 E [ R − b ( s ) ] \mathbb{E}[R-b(s)] E[R−b(s)]，这相当于将期望奖励整体下移了一个固定值即 b ( s ) b(s) b(s) 的期望

这个方法的精妙之处在于：这个数值完全不依赖于策略 π \pi π，展开来看，虽然表达式包含对状态 s s s 的概率分布 p ( s ) p(s) p(s) 积分以及策略 π ( a ∣ s ) \pi(a \mid s) π(a∣s) 的项，当由于对给定状态 s s s 的策略动作积分恒等于 1，最终结果依然保持简洁性，这意味着该结果完全不受策略影响

显然，优化期望奖励 R 与优化 R 减去这个基线的期望是等价的，因为被减去的不过是个常数项，这就是基线方法的核心理念，它完整保留了原始优化问题的本质

现在，如果对这个新目标函数执行原始策略梯度法，本质上就是采样状态 s s s 和动作 a a a 后，直接计算 R ( s , a ) − b ( s ) R(s,a)-b(s) R(s,a)−b(s) 这个差值，也就是 ∇ log ⁡ π ( a ∣ s )   ( R ( s , a ) − b ( s ) ) \nabla \log \pi(a \mid s)\, \left(R(s, a)-b(s)\right) ∇logπ(a∣s)(R(s,a)−b(s))，注意这个性质具有普适性，它对任意状态概率分布 p ( s ) p(s) p(s) 都成立，概率 p ( s ) p(s) p(s) 与动作 a a a 无关（正如当前参数设定所示），该结论就成立，因此只要不依赖动作 a a a，该推导就始终有效

那么问题来了：在所有可能的状态函数 b ( s ) b(s) b(s) 中，我们究竟该选用哪一个呢？让我们通过下面这个双状态示例来建立直观理解

我们将做出如下假设：假设初始策略是在所有状态 s s s 和动作 a a a 上的均匀分布，且初始策略梯度 ∇ π ( a ∣ s ) \nabla \pi(a \mid s) ∇π(a∣s) 暂设为 1，以便简化当前分析

naive_variance = torch.std(torch.tensor([11., 9, 0, 2]))  # @inspect naive_variance

观察梯度方差时可以发现：有时得到 11，有时得到 9，有时为 0，有时为 2，最终计算出的方差值为 5.3

如果我们设定基线值 b(s1) 状态为 10，b(s2) 状态为 1，现在观察会发生什么变化：

baseline_variance = torch.std(torch.tensor([11. - 10, 9 - 10, 0 - 1, 2 - 1]))  # @inspect baseline_variance

此时从奖励值中减去对应的基线值，对于状态 s1，我们减去基线值 10，而对于状态 s2，则减去基线值 1，现在可以看到，基线的方差大幅降低了，此时方差仅为 1.1，我们将方差从 5 降到了 1，效果相当显著，通过简单地减去一个基线值就能实现，而且这并不会影响最终结果的期望值，这里隐含着一个前提假设：状态分布 p ( s ) p(s) p(s) 的期望与策略 π \pi π 无关

Q & A

Q：我在思考，是否可以采用初始冻结策略的参数来初始化基线 b？

A：这个问题提得很好，基线函数 b(s) 的设计本就不应依赖于当前策略，你的问题是：能否直接使用初始策略的状态价值函数作为基线 b(s)？在强化学习中，需要特别注意哪些量是常量、哪些是变量，这确实是个关键点，确实，你完全可以将一个冻结模型作为常量来使用，只要表达式不依赖于该模型，且实际处理时将其视为常量，不进行反向传播求导就完全没问题，这意味着在进行采样和策略更新时，必须保留该策略的旧版本副本，因为一旦基线策略发生变化，就可能陷入基线不再保持恒定的异常情况。

Q ：那么接下来我要追问：如果我们将 π \pi π 可视化为上一步（即上一轮迭代）的策略呢？而非使用最初版本的策略

A：确实可以这样操作，通常的做法是：我们会维护一个策略函数，这个策略会作为旧策略（或称 anchor）使用一段时间，或者在使用 PPO 算法时，我们会先固定价值函数一段时间，进行若干次更新后再同步更新它，实际操作中确实是这样处理的，但实际应用中，开发者往往会采取各种变通做法。

我们通过这个示例证明，至少在这种情况下，经验性地设定某个基线确实能够降低方差，这个例子生动展示了基线方法在实际应用中的显著效果，方差越低，收敛速度越快

你可能会思考，究竟什么样的基线才是最优选择，经过数学推导可以发现，这个问题实际上存在一个非常简洁的闭式解：

b ∗ ( s ) = E  ⁣ [ ( ∇ log ⁡ π ( a ∣ s ) ) 2   R ∣ s ] E  ⁣ [ ( ∇ log ⁡ π ( a ∣ s ) ) 2 ∣ s ] b^*(s) = \frac{ \mathbb{E}\!\left[ \left( \nabla \log \pi(a \mid s) \right)^2 \, R \mid s \right] }{ \mathbb{E}\!\left[ \left( \nabla \log \pi(a \mid s) \right)^2 \mid s \right] } b∗(s)=E[(∇logπ(a∣s))2∣s]E[(∇logπ(a∣s))2R∣s]

该结论适用于单参数模型，若涉及多维情况，则需要考虑协方差的影响，该表达式可以表示为：导数平方与奖励 R 乘积的期望值，除以不含 R 的相同表达式，这种计算通常相当繁琐，特别是在高维情况下尤为明显，由于这个表达式最终会涉及协方差项的计算，通常的做法是直接忽略这些复杂因素，简单地将基线设定为给定状态 s 下的期望奖励即 b ( s ) = E [ R ∣ s ] b(s) = \mathbb{E}[R \mid s] b(s)=E[R∣s]

这种做法并非最优解，但作为启发式方法还算实用。即便如此，这个期望值本身也无法精确计算，因为任何涉及期望值的运算都无法直接求解，只能通过估计来近似求解

不过，这倒为如何选择基线提供了一个很好的指导原则，它代表给定状态下的期望奖励值，简单回顾一下，我们之前讨论的最基础的策略梯度方法，我们可以引入这个基线函数，它对任意状态 s 下的 b(s) 都成立，由此我们得出一个结论：如果能设法估算出给定状态 s 下的期望奖励，这或许会是个不错的选择

3.3 Advantage functions

这一特定选择与优势函数存在关联，在强化学习中，通常会有一个价值函数 V ( s ) = E [ R ∣ s ] V(s) = \mathbb{E}[R \mid s] V(s)=E[R∣s]，它表示给定状态下的预期奖励，而 Q 函数 Q ( s , a ) = E [ R ∣ s , a ] Q(s, a) = \mathbb{E}[R \mid s, a] Q(s,a)=E[R∣s,a] 则表示给定状态和动作下的预期奖励，需要注意的是，这里的 Q 和 R 是相同的，因为我们假设结果奖励包含了所有可能的动作，通常来说，R 代表从该状态出发获得的总回报，而不仅仅是单步奖励，目前这两者是相同的

优势函数的定义就是： A ( s , a ) = Q ( s , a ) − V ( s ) A(s, a) = Q(s, a) - V(s) A(s,a)=Q(s,a)−V(s)，采取某个动作获得的奖励减去所有可能动作的平均奖励，具体来说，它衡量的是动作 a 比从状态 s 获得的期望值优越多少，选择优势函数 A A A 而非单纯依赖基线方式的策略梯度方法有何优势呢？

那么，如果你看 b ( s ) = E [ R ∣ s ] b(s) = \mathbb{E}[R \mid s] b(s)=E[R∣s] 这个等式，b 等于我们之前讨论过的启发式形式，那么只需减去状态值函数的基线奖励就等同于优势函数，即 A ( s , a ) = E [ R ∣ s , a ] − b ( s ) A(s, a)= \mathbb{E}[R \mid s, a] - b(s) A(s,a)=E[R∣s,a]−b(s)，因此可以这样理解：当你选择这种特定形式的基线形式时，实际上就等同于在优化优势函数，这样解释是为了让你更直观地理解基线的作用原理

通常来说，我们很可能会偏离 E  ⁣ [ ∇ log ⁡ π ( a ∣ s )   R ( s , a ) ] \mathbb{E}\!\left[ \nabla \log \pi(a \mid s)\, R(s, a) \right] E[∇logπ(a∣s)R(s,a)] 这个理想方案，因为我们无法精确计算这些期望值，所以得另辟蹊径，具体来说，我们就用 δ \delta δ 来表示代入估计值的任意量即 E  ⁣ [ ∇ log ⁡ π ( a ∣ s )   δ ] \mathbb{E}\!\left[ \nabla \log \pi(a \mid s)\, \delta \right] E[∇logπ(a∣s)δ]

所有方法本质上都是对策略的对数求梯度，然后乘以一个基于奖励的变量，所有算法 -- 无论是 PPO 还是 GRPO -- 都遵循这样的基本流程：先进行策略展开获得动作，现在的问题是：你希望朝这个动作方向调整多少，具体调整幅度取决于获得的奖励值，因此可以将奖励值代入对应位置，这就是最基础的策略梯度方法

可以采用奖励减去期望估计值的方式，还可以除以标准差，这正是我们稍后会讲到的 GRPO 算法的做法，但 E  ⁣ [ ∇ log ⁡ π ( a ∣ s )   δ ] \mathbb{E}\!\left[ \nabla \log \pi(a \mid s)\, \delta \right] E[∇logπ(a∣s)δ] 是通用形式，具体采用哪种先验形式并不那么重要，因为明年可能就会出现 GRPO 2 之类的改进版本，不过这些关于策略梯度的内容，明年我们还会继续讲授同样的课程

如果大家想了解更多强化学习的推导过程和直观理解，可以参考 Chelsea 的深度强化学习课程 [CS224R lecture notes]

Q & A

Q：基线这个概念本身是什么意思？

A ：基线的定义是：基线可以是任意仅依赖于状态 s（或状态 - 动作对（s,a））的函数 b(s)（或 b(s,a)），这正是我们在策略梯度算法中实际使用的概念，可以这样理解，简而言之，策略梯度的更新就是基于 ∇ log ⁡ π ( a ∣ s )   ( R ( s , a ) − b ( s ) ) \nabla \log \pi(a \mid s)\, \left(R(s, a)-b(s)\right) ∇logπ(a∣s)(R(s,a)−b(s)) 这个原理进行的，而基线就是你在此处选择的任意函数，熟悉控制变量法的观众会发现，这本质上就是统计学里的同一个概念。

4. Training walkthrough

现在，让我们试着更深入地探讨这个问题

我们将定义一个简单的模型和任务，并逐步解析一段代码，这段代码可能与作业五相似，也可能不尽相同，我们还将尝试实际运行一些实验

本次讲解主要基于 GRPO（Group Relative Policy Optimization）算法 [Shao+ 2024] 展开，这里有个有趣的传承脉络：先是 PPO 算法，而后的 GRPO 其实是对 PPO 的简化改进，而非全新算法体系，大家可以从简单入手，逐步增加复杂度

事实上，GRPO 能在 2024 年出现是因为语言模型场景天然具备适合 GRPO 的结构特性，在传统强化学习场景中，比如让机器人学走路，GRPO 这种算法其实很难自然适用，关键在于，语言模型有个独特优势：给定一个提示词（prompt），就能基于它生成大量响应样本，这种特性天然形成了用于计算基线的分组结构，实际上这个基线就是所有响应样本奖励的平均值

我们的核心目标是最小化方差，而分组结构天然构成了对比样本集，这正是其相对性原理的体现，这种评估本质上是相对于同组样本而言的，反之，如果每次生成的响应都截然不同，缺乏天然的分组结构，那么 GRPO（分组相对策略优化）就失去了应用基础，此时就必须另寻他法。通常而言，这种替代方法往往会采用价值函数，通过对所有可能状态和动作进行聚合计算来实现评估

而在当前情景下，由于语言模型的特性，我们实际上获得的是对所有可能响应的经验性估计，这种估计无需穷尽所有可能性

以下是算法伪代码实现：

稍后我们将用实际 Python 代码进行解析，我们先在此展示伪代码框架

4.1 Simple task

现在让我们定义一个简单任务场景，我们需要设计一个足够简单的任务场景，使得能在笔记本电脑上直接训练一个基础模型，而无需运行完整的语言模型架构，于是有一个基础任务场景：对 n 个数字进行排序

prompt = [1, 0, 2]
response = [0, 1, 2]

具体而言，输入提示是 n 个数字，期望模型的输出是经过排序的 n 个数字，接下来需要定义奖励函数来完成这个环境的构建

这个奖励函数需要量化模型输出结果与标准排序答案的接近程度，这里我们立刻就能发现奖励函数设计的关键所在，强化学习最有趣的特点之一，就是奖励函数可以通过多种方式灵活定义

比如，你可以将奖励函数定义为：若输出结果正确排序则奖励值为 1，否则为 0，这应该就是你最关心的核心指标，但你应该记得稀疏奖励这个经典难题，如果初始策略几乎不产生有效动作，那么绝大多数情况下都只能获 0 奖励，这样模型就难以取得实质性的进步

所以，我们需要定义一个能提供部分奖励的评分机制，我们可以把奖励值定义为：模型输出结果与标准答案匹配的正确位置数量，具体实现代码如下所示：

def sort_distance_reward(prompt: list[int], response: list[int]) -> float:  # @inspect prompt, @inspect response
    """
    Return how close response is to ground_truth = sorted(prompt).
    In particular, compute number of positions where the response matches the ground truth.
    """
    assert len(prompt) == len(response)
    ground_truth = sorted(prompt)
    return sum(1 for x, y in zip(response, ground_truth) if x == y)

这里将输入的提示词排序好后的结果作为 ground truth 也就是我们的标准答案，然后与我们的响应做对比，只需统计模型输出响应与标准答案相匹配的字符位置数量即可

reward = sort_distance_reward([3, 1, 0, 2], [0, 1, 2, 3])  # @inspect reward

因此正确答案的奖励值为 4 分，匹配了 4 个字符位置

reward = sort_distance_reward([3, 1, 0, 2], [7, 2, 2, 5])  # @inspect reward  @stepover

若输出结果未能有效完成任务，则奖励值仅为 1 分，因为你在第二个位置恰好蒙对了数字 2，这纯属运气

  reward = sort_distance_reward([3, 1, 0, 2], [0, 3, 1, 2])  # @inspect reward  @stepover

而上面这种情况同样未能解决问题，但观察这个结果会发现，它确实在认真尝试解决问题，由于数字 0 的位置正确，这次你依然得到 1 分

这便是一种可行的奖励机制，你可能对此并不满意，因为当前结果与预期相差甚远，而第一次的结果更接近目标，但令人费解的是，第二次和第三次这些结果都获得了相同的 1 分奖励

因此，我们需要设计一种能提供梯度评分的替代性奖励机制，现在我们将采用如下的评分规则：

def sort_inclusion_ordering_reward(prompt: list[int], response: list[int]) -> float:  # @inspect prompt, @inspect response
    """
    Return how close response is to ground_truth = sorted(prompt).
    """
    assert len(prompt) == len(response)

    # Give one point for each token in the prompt that shows up in the response
    inclusion_reward = sum(1 for x in prompt if x in response)  # @inspect inclusion_reward

    # Give one point for each adjacent pair in response that's sorted
    ordering_reward = sum(1 for x, y in zip(response, response[1:]) if x <= y)  # @inspect ordering_reward

    return inclusion_reward + ordering_reward

reward = sort_inclusion_ordering_reward([3, 1, 0, 2], [0, 1, 2, 3])  # @inspect reward

响应中每出现一个提示词，就计 1 分，这样至少能确保输出结果包含输入中的 tokens，这个要求并不过分，以上面这个具体案例来说，我们获得了 4 分的包含性奖励。此外，回答中每出现一组相邻且有序的词对，还能额外获得 1 分，因此这部分的得分是 3 分，因为共有 3 组相邻有序的词对，最终奖励是各部分得分的总和，所以总分是 7 分

细心的你可能已经发现，这个奖励机制其实存在一个漏洞，不过这个漏洞就留给大家自己发现吧，在强化学习任务中，我们会给予大量部分得分，也就是这里的 inclusion 得分和 ordering 得分

下面我们简单提下可能存在的漏洞：(from ChatGPT)

漏洞就在下面这句代码：

inclusion_reward = sum(1 for x in prompt if x in response)

这里用的是集合式包含，而不是多重集合的包含（计数/次数），也就是说：

• 只要 response 里出现过一次 x，那么 prompt 里所有等于 x 的位置都会各自拿到 1 分
• 它不检查出现次数是否匹配，比如 prompt 里有两个 1，response 里只有一个 1 也能拿满这两分

这就给了一个作弊空间：当 prompt 里有重复数字时，你可以漏掉某些重复元素，用别的数字顶上去，仍然拿到满分的包含性奖励；再把 response 排成非递减，就能把 ordering 分也吃满

例如下面这个示例：

prompt   = [1, 1, 2, 3]
response = [1, 2, 3, 3]   # 注意：少了一个 1，多了一个 3（并不是 prompt 的排序结果）

在这个示例中，response 能把 inclusion 和 ordering 奖励都拿满，得到最高分 7 分，但显然这个 response 并不是我们真正想要的 ground truth

也就是说，如果我们的 prompt 示例中没有重复元素，那么这个 "次数漏洞" 确实触发不了，但一旦允许出现重复，这个奖励就会被上面这种方式骗分。

以上就是任务的全部内容，通常来说，我们会采用第二种奖励函数，任务要求已经很明确了，这就是我们的训练环境

4.2 Simple model

现在，我们来定义一个解决该任务的模型，我们将定义一个非常简单的模型，我们假设提示词和生成回复的长度固定且相同，我们将尝试用独立的位置参数来捕捉位置信息，毕竟在这个场景中，位置信息才是关键所在，因为它对排序至关重要

我们准备采用的方法是：对响应中的每个位置进行独立解码，因此这并非回归模型，我们将直接对序列进行编码，然后分别输出所有 token，这通常不是实际应用中的理想做法，当然 speculative decoding 这类特殊情况除外，适度采用这种方法可能带来益处，但采用这种自回归生成方法能让代码更加简洁

以下是模型架构：

class Model(nn.Module):
    def __init__(self, vocab_size: int, embedding_dim: int, prompt_length: int, response_length: int):
        super().__init__()
        self.embedding_dim = embedding_dim
        self.embedding = nn.Embedding(vocab_size, embedding_dim)
        # For each position, we have a matrix for encoding and a matrix for decoding
        self.encode_weights = nn.Parameter(torch.randn(prompt_length, embedding_dim, embedding_dim) / math.sqrt(embedding_dim))
        self.decode_weights = nn.Parameter(torch.randn(response_length, embedding_dim, embedding_dim) / math.sqrt(embedding_dim))

    def forward(self, prompts: torch.Tensor) -> torch.Tensor:
        """
        Args:
            prompts: int[batch pos]
        Returns:
            logits: float[batch pos vocab]
        """
        # Embed the prompts
        embeddings = self.embedding(prompts)   # [batch pos dim]

        # Transform using per prompt position matrix, collapse into one vector
        encoded = einsum(embeddings, self.encode_weights, "batch pos dim1, pos dim1 dim2 -> batch dim2")

        # Turn into one vector per response position
        decoded = einsum(encoded, self.decode_weights, "batch dim2, pos dim2 dim1 -> batch pos dim1")

        # Convert to logits (input and output share embeddings)
        logits = einsum(decoded, self.embedding.weight, "batch pos dim1, vocab dim1 -> batch pos vocab")

        return logits

model = Model(vocab_size=3, embedding_dim=10, prompt_length=3, response_length=3)

模型结构中包含嵌入矩阵，每个位置还配置了两组变换矩阵，一组用于编码，另一组用于解码，这部分通过前向传播过程会更容易说明

prompts = torch.tensor([[1, 0, 2]])  # [batch pos]

初始输入是一个提示词，我们将统一采用 [batch pos] 这种表示法来标注张量维度，这里存在一个 batch 维度，对应着样本数量和提示词数量，其次是位置维度，这显然表示当前所处的序列位置

接下来我们将生成对应的响应内容，这是推理过程，让我们逐步解析这个过程：

def generate_responses(prompts: torch.Tensor, model: Model, num_responses: int) -> torch.Tensor:
    """
    Args:
        prompts (int[batch pos])
    Returns:
        generated responses: int[batch trial pos]

    Example (batch_size = 3, prompt_length = 3, num_responses = 2, response_length = 4)
    p1 p1 p1 r1 r1 r1 r1
             r2 r2 r2 r2
    p2 p2 p2 r3 r3 r3 r3
             r4 r4 r4 r4
    p3 p3 p3 r5 r5 r5 r5
             r6 r6 r6 r6
    """
    logits = model(prompts)  # [batch pos vocab]
    batch_size = prompts.shape[0]

    # Sample num_responses (independently) for each [batch pos]
    flattened_logits = rearrange(logits, "batch pos vocab -> (batch pos) vocab")
    flattened_responses = torch.multinomial(softmax(flattened_logits, dim=-1), num_samples=num_responses, replacement=True)  # [batch pos trial]
    responses = rearrange(flattened_responses, "(batch pos) trial -> batch trial pos", batch=batch_size)
    return responses

torch.manual_seed(10)
responses = generate_responses(prompts=prompts, model=model, num_responses=5)  # [batch trial pos]  @inspect responses

这里先介绍几个术语，当前批次大小即此处的提示词数量，每个提示词的长度固定为 3，本例中每个提示词将生成 5 个响应结果，而每个响应结果的长度为 3，在排序任务中，响应长度与提示长度保持一致

首先，我们会将提示输入模型以获取逻辑值（logits），这将为每个提示的每个位置生成对应的 token 概率分布

class Model(nn.Module):
    def __init__(self, vocab_size: int, embedding_dim: int, prompt_length: int, response_length: int):
        pass

    def forward(self, prompts: torch.Tensor) -> torch.Tensor:
        """
        Args:
            prompts: int[batch pos]
        Returns:
            logits: float[batch pos vocab]
        """
        # Embed the prompts
        embeddings = self.embedding(prompts)   # [batch pos dim]

        # Transform using per prompt position matrix, collapse into one vector
        encoded = einsum(embeddings, self.encode_weights, "batch pos dim1, pos dim1 dim2 -> batch dim2")

        # Turn into one vector per response position
        decoded = einsum(encoded, self.decode_weights, "batch dim2, pos dim2 dim1 -> batch pos dim1")

        # Convert to logits (input and output share embeddings)
        logits = einsum(decoded, self.embedding.weight, "batch pos dim1, vocab dim1 -> batch pos vocab")

        return logits

具体操作是：我们会将这些提示词嵌入到特定维度的向量空间中，接着使用每个提示位置对应的矩阵进行变换处理，然后将其压缩降维，使用 einsum 处理后我们得到了批处理位置维度为 1 的数据结构，然后 self.embedding.weight 这个权重会对每个位置执行从维度 1 到维度 2 的转换，最终得到批处理维度为 2 的结果，这样我们就完成了对位置维度和 dim1 的求和运算

基于每个提示对应的向量，我们将为每个位置应用矩阵变换，最终返回一个新的向量。最后，基于提示中每个位置对应的向量，我们会将其转换为词汇表上的 logits（对数概率），这个模型很简单，但它恰好能解释这个简单的示例

我们得到 logits 值后，为了应对 pytorch 中 multinomial 函数需要扁平化输入的特殊要求，我们要把 logits 这个张量展平成 (批次数 x 位置数) x 词表大小 的二维格式。接着我们要对模型响应进行采样，这样就会得到维度为 (批次数 x 位置数 x 采样次数) 的输出，我们把采样次数这个维度命名为 trial，简单来说，我们会重新调整数据结构，让每个提示对应每个采样批次都能生成一组完整的示例序列，这样处理很合理

通常在这个环节，我们会调用 vLLM 进行推理计算，这里采用这个方式只是因为当前模型结构非常简单，整个流程都可以用矩阵运算来实现，由于我们是从同一个对数概率分布中进行采样的，因此这些响应必然会高度相似，但这与直接从语言模型中采样生成的情况并无二致，唯一区别在于语言模型采样自回归方式生成，而这里采样的是独立采样

我们得到响应结果后就可以为所有这些响应计算奖励值

def compute_reward(prompts: torch.Tensor, responses: torch.Tensor, reward_fn: Callable[[list[int], list[int]], float]) -> torch.Tensor:
    """
    Args:
        prompts (int[batch pos])
        responses (int[batch trial pos])
    Returns:
        rewards (float[batch trial])
    """
    batch_size, num_responses, _ = responses.shape
    rewards = torch.empty(batch_size, num_responses, dtype=torch.float32)
    for i in range(batch_size):
        for j in range(num_responses):
            rewards[i, j] = reward_fn(prompts[i, :], responses[i, j, :])
    return rewards

rewards = compute_reward(prompts=prompts, responses=responses, reward_fn=sort_inclusion_ordering_reward)  # [batch trial]  @inspect rewards

对于每个提示和对应的响应，我们只需调用之前讨论过的奖励函数即可，这部分没什么特别之处

def compute_deltas(rewards: torch.Tensor, mode: str) -> torch.Tensor:  # @inspect rewards
    """
    Args:
        rewards (float[batch trial])
    Returns:
        deltas (float[batch trial]) which are advantage-like quantities for updating
    """
    if mode == "rewards":
        return rewards

    if mode == "centered_rewards":
        # Compute mean over all the responses (trial) for each prompt (batch)
        mean_rewards = rewards.mean(dim=-1, keepdim=True)  # @inspect mean_rewards
        centered_rewards = rewards - mean_rewards  # @inspect centered_rewards
        return centered_rewards

    if mode == "normalized_rewards":
        mean_rewards = rewards.mean(dim=-1, keepdim=True)  # @inspect mean_rewards
        std_rewards = rewards.std(dim=-1, keepdim=True)  # @inspect std_rewards
        centered_rewards = rewards - mean_rewards  # @inspect centered_rewards
        normalized_rewards = centered_rewards / (std_rewards + 1e-5)  # @inspect normalized_rewards
        return normalized_rewards

    if mode == "max_rewards":
        # Zero out any reward that isn't the maximum for each batch
        max_rewards = rewards.max(dim=-1, keepdim=True)[0]
        max_rewards = torch.where(rewards == max_rewards, rewards, torch.zeros_like(rewards))
        return max_rewards

    raise ValueError(f"Unknown mode: {mode}")

deltas = compute_deltas(rewards=rewards, mode="rewards")  # [batch trial]  @inspect deltas
deltas = compute_deltas(rewards=rewards, mode="centered_rewards")  # [batch trial]  @inspect deltas
deltas = compute_deltas(rewards=rewards, mode="normalized_rewards")  # [batch trial]  @inspect deltas
deltas = compute_deltas(rewards=rewards, mode="max_rewards")  # [batch trial]  @inspect deltas

接着下面这个名为 compute_deltas 的函数，其作用是将奖励值转换为后续更新所需的 delta 值，这个框架提供了多种实现方式，部分方案大家可以在作业中进行探索，比如，你可以直接让 delta 等于奖励值（"rewards"），也可以对奖励值进行中心化处理（"centered_rewards"），首先计算每个提示对应的所有响应得分的平均值，然后只需减去这个均值就能得到中心化后的奖励值

回答下之前的问题：当奖励值呈现一个 1 和大量 0 时，假设其均值约为 0.1，此时若进行均值减法运算，最终会得到大量 -0.1 和略低于 1 的数值，因此，那些负样本同样会参与模型参数的更新过程，这就是奖励中心化的作用

在 GRPO 中，你还可以进行标准化处理（"normalized_rewards"），首先对奖励值进行中心化处理，然后除以其标准差并添加一个微小常数，这样可以避免出现除以 0 的情况，最终返回处理后的结果。这里需要注意一个问题，设想下这样一种情况：如果策略模型对所有生成内容都给出相同的奖励值，那么针对该样本实际上不会进行任何参数更新，这种机制是否合理取决于你的具体优化目标，但核心原理在于：这种情况下梯度为 0

在这个样本组内部进行相对比较时，由于所有样本的奖励值相同，因此没有理由偏向其中任何一个特定样本，因此系统会主动放弃更新，转而期待其他样本能提供有效的梯度信号。归一化处理意味着：无论奖励值是 10 还是放大 100 倍后的 1000，经过标准化后的奖励值都会保持尺度不变性，这正是该方法的优势所在

有趣的是，论文虽未提及但有个值得尝试的巧妙思路 -- 你也可以将每个批次中非最大值的奖励全部归零（"max_rewards"），这个思路源自强化学习中常见的局部最优困境，当算法给予次优行为过多 "部分奖励" 时，策略模型往往会固守这些唾手可得的低价值目标，反而放弃追求更高回报的机会，因此可以尝试设定：只要不是最高奖励的行为就完全不予鼓励，这本质上是一种非全既无的激励机制

目前我们的操作流程是：首先生成若干响应，随后计算对应的奖励值，上面这些差值（deltas）为模型更新提供了依据，现在需要引入另一个关键要素：各响应对应的对数概率，因为在策略梯度的公式中，更新量等于奖励差值乘以策略对数概率的梯度，即 δ ⋅ ∇ log ⁡ π \delta \cdot \nabla \log \pi δ⋅∇logπ

def compute_log_probs(prompts: torch.Tensor, responses: torch.Tensor, model: Model) -> torch.Tensor:
    """
    Args:
        prompts (int[batch pos])
        responses (int[batch trial pos])
    Returns:
        log_probs (float[batch trial pos]) under the model
    """
    # Compute log prob of responses under model
    logits = model(prompts)  # [batch pos vocab]
    log_probs = F.log_softmax(logits, dim=-1)  # [batch pos vocab]

    # Replicate to align with responses
    num_responses = responses.shape[1]
    log_probs = repeat(log_probs, "batch pos vocab -> batch trial pos vocab", trial=num_responses)  # [batch trial pos vocab]

    # Index into log_probs using responses
    log_probs = log_probs.gather(dim=-1, index=responses.unsqueeze(-1)).squeeze(-1)  # [batch trial pos]

    return log_probs

log_probs = compute_log_probs(prompts=prompts, responses=responses, model=model)  # [batch trial]  @inspect log_probs

这部分逻辑同样清晰明了，将数据输入模型后把逻辑值（logits）转换为对数概率（log probs），由于提示词仅存在于批次维度，而响应数据多出一个维度，这里需要进行特殊处理，我们需要将这些对数概率向上转型到更高维度的张量结构，我们将使用响应数据作为索引来提取对应的对数概率，响应数据本质上为每个批次采样位置指定了需要提取的对数概率索引，因此原来的 log_probs 这个张量结构是 批次 x 采样次数 x 位置数 x 词表大小 的维度排布，变换之后的张量结构是 批次 x 采样次数 x 位置数 的维度排布，其中每个位置存储着索引值，这样操作就能得到 批次 x 采样次数 x 位置数 维度的输出结果

模型返回的 logits 为每个位置和提示词提供了整个词表上的概率分布，现在，我们已经获得了特定响应序列的对数概率值，其具体数值如上图所示

现在，我们终于要计算损失函数了，而损失函数这里又涉及到一系列的选择方案：

def compute_loss(log_probs: torch.Tensor, deltas: torch.Tensor, mode: str, old_log_probs: torch.Tensor | None = None) -> torch.Tensor:
    if mode == "naive":
        return -einsum(log_probs, deltas, "batch trial pos, batch trial -> batch trial pos").mean()

    if mode == "unclipped":
        ratios = log_probs / old_log_probs  # [batch trial]
        return -einsum(ratios, deltas, "batch trial pos, batch trial -> batch trial pos").mean()

    if mode == "clipped":
        epsilon = 0.01
        unclipped_ratios = log_probs / old_log_probs  # [batch trial]
        unclipped = einsum(unclipped_ratios, deltas, "batch trial pos, batch trial -> batch trial pos")

        clipped_ratios = torch.clamp(unclipped_ratios, min=1 - epsilon, max=1 + epsilon)
        clipped = einsum(clipped_ratios, deltas, "batch trial pos, batch trial -> batch trial pos")
        return -torch.minimum(unclipped, clipped).mean()

    raise ValueError(f"Unknown mode: {mode}")

loss = compute_loss(log_probs=log_probs, deltas=deltas, mode="naive")  # @inspect loss

freezing_parameters()

old_model = Model(vocab_size=3, embedding_dim=10, prompt_length=3, response_length=3)  # Pretend this is an old checkpoint @stepover
old_log_probs = compute_log_probs(prompts=prompts, responses=responses, model=old_model)  # @stepover
loss = compute_loss(log_probs=log_probs, deltas=deltas, mode="unclipped", old_log_probs=old_log_probs)  # @inspect loss
loss = compute_loss(log_probs=log_probs, deltas=deltas, mode="clipped", old_log_probs=old_log_probs)  # @inspect loss

最基础的做法是原始策略梯度法（"naive"），只需将奖励差异值与对数概率相乘后取均值即可，由于我们使用的是结果奖励机制，这里的关键在于奖励差值（deltas）与位置无关，本质上，每个位置都会接收奖励差值被广播到所有位置，如果采用过程奖励机制，那么这些奖励差值也会按位置单独计算，这就是最基础的处理方式

接着让我们来简单聊聊冻结参数这个函数：

def freezing_parameters():
    # Motivation: in GRPO you'll see ratios: p(a | s) / p_old(a | s)
    # When you're optimizing, it is important to freeze and not differentiate through p_old
    w = torch.tensor(2., requires_grad=True)
    p = torch.nn.Sigmoid()(w)
    p_old = torch.nn.Sigmoid()(w)
    ratio = p / p_old
    ratio.backward()
    grad = w.grad  # @inspect grad

    # Do it properly:
    w = torch.tensor(2., requires_grad=True)
    p = torch.nn.Sigmoid()(w)
    with torch.no_grad():  # Important: treat p_old as a constant!
        p_old = torch.nn.Sigmoid()(w)
    ratio = p / p_old
    ratio.backward()
    grad = w.grad  # @inspect grad

稍后在 GRPO 算法中，我们会看到 p ( a ∣ s ) p old ( a ∣ s ) \frac{p(a \mid s)}{p_\text{old}(a \mid s)} pold(a∣s)p(a∣s) 这些比例参数，这涉及到核心概念：用给定状态 s 下的动作概率除以另一个模型的输出概率，关键是要记住必须冻结 p old p_\text{old} pold 参数，且不能对其进行微分求导

举个简单的示例来说明，假设我们有一个单一参数 w，这个参数同时控制着两个概率分布，我们可以将其视为一个策略函数，在当前这个迭代步骤中，旧参数值恰好与新参数相同，现在，如果我们计算比率并执行反向传播会发生什么？梯度会是多少？这里我们用 p 除以 p_old，因此这个比值将等于 1，而 1 的梯度为零，这样一来梯度为零，显然没什么用处

正确的做法是：像往常一样处理你的 p，而对于需要视为常量的部分，就用 "no_grad" 包装起来，这样就能获取数值结果同时避免保留整个计算图，然后直接用这个数值结果做除法运算，现在梯度就不会为零了

注意强化学习与预训练不同，在 RL 中，多个数值可能分别依赖于新旧不同的参数体系

Q & A

Q：为什么我们在回溯序列时不将结果奖励进行折现呢？

A：我猜你可能想问的是一个假设：最后 100 个 token 比前 100 个更重要，问题在于：当存在结果奖励时，为何不采用某种折现机制？或许最后 100 个 token 比最初的 100 个 token 更为关键，这个观点似乎并不那么明确，确实，最后那些正在生成答案的 token 显然至关重要，但问题在于，在强化学习中通常需要进行信用分配，早期做出的某些决策显然至关重要，事实上，它们的影响可能比最终结果更为深远，因为只要确立了正确的决策，后续的发展往往就会水到渠成，强化学习的难点恰恰在于难以确定信用分配的节点，尤其是在奖励信号稀疏的情况下，我认为在当前场景下，我们只能将功劳或过失平均分摊到整个决策过程中。

经过这段铺垫，我们就能更好理解 GRPO 损失函数的计算原理

假设我们有一个旧模型（old_model），我们将利用这个旧模型来计算响应序列的对数概率（old_log_probs），我们跳过未裁剪的版本（"unclipped"），直接看经过裁剪的版本（clipped），这就是 GRPO 损失函数，我们取当前模型的对数概率，再除以上一轮迭代的对数概率值，请注意，这个分母（old_log_probs）应当是个固定值，这里似乎忘记给旧对数概率值加上梯度截断了，不过你应该知道该怎么处理

我们计算 log_probs / old_log_probs 这个概率比，然后用它乘以 delta 值，如果直接采用简单方法，只需将对数概率乘以 delta 即可，这本质上是一样的操作，只不过我们把所有对数乘积都除了一遍，反正 old_log_probs 是个常数项，其实我们只是在对梯度进行缩放

现在还有另一个操作我们进行了截断处理，我们之所以要先计算 unclipped_ratios 这个概率比，就是为了把梯度截断在 1 − ϵ 1-\epsilon 1−ϵ 和 1 + ϵ 1+\epsilon 1+ϵ 之间，这样做是为了确保概率比不会偏离得太离谱，同时我们还要将这些截断后的概率比乘以 delta，最后我们会取最小值并返回结果，由于讨论的是奖励值，我们需要加个负号将其转换为损失函数

这正是按照 GRPO 论文中的数学推导来实现的，在作业中，你会看到关于这种处理方式合理性的详细说明，因此，只要更新幅度在截断范围内，系统就会执行标准更新操作，但当更新比例超过该范围时，更新幅度将被限制在 1 − ϵ 1 - \epsilon 1−ϵ 到 1 + ϵ 1 + \epsilon 1+ϵ 的区间内

此外还引入了 KL 惩罚项作为额外的正则化手段：

K L ( p   ∥   q ) = E x ∼ p [ log ⁡ p ( x ) q ( x ) ] , = E x ∼ p [ − log ⁡ q ( x ) p ( x ) ] , = E x ∼ p [ q ( x ) p ( x ) − log ⁡ q ( x ) p ( x ) − 1 ] \begin{aligned} \mathrm{KL}(p \,\|\, q) &= \mathbb{E}{x \sim p} \left[ \log \frac{p(x)}{q(x)} \right], \\[6pt] &= \mathbb{E}{x \sim p} \left[ - \log \frac{q(x)}{p(x)} \right], \\[6pt] &= \mathbb{E}_{x \sim p} \left[ \frac{q(x)}{p(x)}- \log \frac{q(x)}{p(x)}- 1 \right] \end{aligned} KL(p∥q)=Ex∼p[logq(x)p(x)],=Ex∼p[−logp(x)q(x)],=Ex∼p[p(x)q(x)−logp(x)q(x)−1]

你应该还记得两个分布之间 KL 散度的定义：从左侧分布采样后，计算该样本在左侧分布与右侧分布的对数概率比，可以将其改写为带符号的 q/p 形式，如果要做 KL 惩罚项，直接套用 E x ∼ p [ − log ⁡ q ( x ) p ( x ) ] \mathbb{E}_{x \sim p}\left[ - \log \frac{q(x)}{p(x)} \right] Ex∼p[−logp(x)q(x)] 这个公式即可，但要注意如果想估算 KL 散度，只需去掉期望运算符就能得到无偏估计

实际上，采用 q ( x ) p ( x ) − log ⁡ q ( x ) p ( x ) − 1 \frac{q(x)}{p(x)}- \log \frac{q(x)}{p(x)}- 1 p(x)q(x)−logp(x)q(x)−1 这种特定估算方式能获得更低的方差，这个式子看起来有点奇怪，但你可以验证两者其实是等价的，因为 E x ∼ p [ q ( x ) p ( x ) ] = 1 \mathbb{E}_{x \sim p}\left[\frac{q(x)}{p(x)} \right]=1 Ex∼p[p(x)q(x)]=1，所以等式必定成立，这个表达式确实比原始方法能给出更准确的 KL 散度估计值

在多数情况下，当我们试图估计期望值时，核心目标就是找到一个无偏（或有时甚至允许有偏）的估计量，关键是这个估计量的方差要比原始简单估计方法更低，因此我们需要重构内部表达式，通过数学变换来降低方差

下面快速实现 KL 惩罚项：

def compute_kl_penalty(log_probs: torch.Tensor, ref_log_probs: torch.Tensor) -> torch.Tensor:
    """
    Compute an estimate of KL(model | ref_model), where the models are given by:
        log_probs [batch trial pos vocab]
        ref_log_probs [batch trial pos vocab]
    Use the estimate:
        KL(p || q) = E_p[q/p - log(q/p) - 1]
    """
    return (torch.exp(ref_log_probs - log_probs) - (ref_log_probs - log_probs) - 1).sum(dim=-1).mean()

kl_penalty = compute_kl_penalty(log_probs=log_probs, ref_log_probs=old_log_probs)  # @inspect kl_penalty

实现起来相当直观，唯一需要注意的是在最后一个维度上进行求和运算，我们是在词汇表大小维度上进行求和，但在批次大小、采样次数和位置数维度上计算均值

综上所述，以下是实现该算法所需的核心组件：

• Generate responses
• Compute rewards R and δ \delta δ (rewards, centered rewards, normalized rewards, max rewards)
• Compute log probs of responses
• Compute loss from log probs and δ \delta δ (naive, unclipped, clipped)

首先使用特定固定模型生成响应，接着根据生成的响应计算奖励值和差值，对于 GRPO 及其同类方法而言，这些计算结果与模型本身无关，这完全取决于生成的响应结果，在设计这类系统架构时，有时奖励机制可以非常简单，可能简单到只需一行代码就能实现精确匹配，有时奖励机制会涉及智能体，执行环境交互，完成各种复杂操作，这个操作可能成本高昂也可能很低廉，但本质上独立于实际模型，除非使用语言模型作为评判器，这种情况下就涉及另一个模型了

与此同时，你可以计算响应的对数概率，然后根据这些对数概率和当前获得的差值来计算损失值，最后将它们组合起来

4.3 Run policy gradient

让我们试着把这些内容整合起来，下面是完整的算法实现，本质上就是将理论框架转化为代码的具体呈现：

def run_policy_gradient(num_epochs: int = 100,
                        num_steps_per_epoch: int = 10,
                        compute_ref_model_period: int = 10,
                        num_responses: int = 10,
                        deltas_mode: str = "rewards",
                        loss_mode: str = "naive",
                        kl_penalty: float = 0.0,
                        reward_fn: Callable[[list[int], list[int]], float] = sort_inclusion_ordering_reward,
                        use_cache: bool = False) -> tuple[str, str]:
    """Train a model using policy gradient.
    Return:
    - Path to the image of the learning curve.
    - Path to the log file
    """
    torch.manual_seed(5)

    image_path = f"var/policy_gradient_{deltas_mode}_{loss_mode}.png"
    log_path = f"var/policy_gradient_{deltas_mode}_{loss_mode}.txt"

    # Already ran, just cache it
    if use_cache and os.path.exists(image_path) and os.path.exists(log_path):
        return image_path, log_path

    # Define the data
    prompts = torch.tensor([[1, 0, 2], [3, 2, 4], [1, 2, 3]])
    vocab_size = prompts.max() + 1
    prompt_length = response_length = prompts.shape[1]

    model = Model(vocab_size=vocab_size, embedding_dim=10, prompt_length=prompt_length, response_length=response_length)
    optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)

    records = []
    ref_log_probs = None
    ref_model = None
    old_log_probs = None

    if use_cache:
        out = open(log_path, "w")
    else:
        out = sys.stdout

    for epoch in tqdm(range(num_epochs), desc="epoch"):
        # If using KL penalty, need to get the reference model (freeze it every few epochs)
        if kl_penalty != 0:
            if epoch % compute_ref_model_period == 0:
                ref_model = model.clone()

        # Sample responses and evaluate their rewards
        responses = generate_responses(prompts=prompts, model=model, num_responses=num_responses)  # [batch trial pos]
        rewards = compute_reward(prompts=prompts, responses=responses, reward_fn=reward_fn)  # [batch trial]
        deltas = compute_deltas(rewards=rewards, mode=deltas_mode)  # [batch trial]

        if kl_penalty != 0:  # Compute under the reference model
            with torch.no_grad():
                ref_log_probs = compute_log_probs(prompts=prompts, responses=responses, model=ref_model)  # [batch trial]

        if loss_mode != "naive":  # Compute under the current model (but freeze while we do the inner steps)
            with torch.no_grad():
                old_log_probs = compute_log_probs(prompts=prompts, responses=responses, model=model)  # [batch trial]

        # Take a number of steps given the responses
        for step in range(num_steps_per_epoch):
            log_probs = compute_log_probs(prompts=prompts, responses=responses, model=model)  # [batch trial]
            loss = compute_loss(log_probs=log_probs, deltas=deltas, mode=loss_mode, old_log_probs=old_log_probs)  # @inspect loss
            if kl_penalty != 0:
                loss += kl_penalty * compute_kl_penalty(log_probs=log_probs, ref_log_probs=ref_log_probs)

            # Print information
            print_information(epoch=epoch, step=step, loss=loss, prompts=prompts, rewards=rewards, responses=responses, log_probs=log_probs, deltas=deltas, out=out)
            global_step = epoch * num_steps_per_epoch + step
            records.append({"epoch": epoch, "step": global_step, "loss": loss.item(), "mean_reward": rewards.mean().item()})

            # Backprop and update parameters
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
    if use_cache:
        out.close()

    if use_cache:
        # Plot step versus loss and reward in two subplots
        steps = [r["step"] for r in records]
        losses = [r["loss"] for r in records]
        rewards = [r["mean_reward"] for r in records]

        fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))

        # Loss subplot
        ax1.plot(steps, losses)
        ax1.set_xlabel("Step")
        ax1.set_ylabel("Train Loss")
        ax1.set_title("Train Loss")

        # Reward subplot
        ax2.plot(steps, rewards)
        ax2.set_xlabel("Step")
        ax2.set_ylabel("Mean Reward")
        ax2.set_title("Mean Reward")

        plt.tight_layout()
        plt.savefig(image_path)
        plt.close()

    return image_path, log_path

run_policy_gradient(num_epochs=1, num_steps_per_epoch=1)

这里我们定义了一个简单的数据集，包含 3 个提示词（prompt），每个提示词长度为 3，接着定义模型、优化器，设置完成后就是多个循环结构和 GRPO 算法实现

for epoch in tqdm(range(num_epochs), desc="epoch"):
    # If using KL penalty, need to get the reference model (freeze it every few epochs)
    if kl_penalty != 0:
        if epoch % compute_ref_model_period == 0:
            ref_model = model.clone()
    ...

最外层是 epoch 循环，这里有个细节处理：当使用 KL 惩罚项时，我们会先冻结模型参数将其作为参考模型，以便进行正则化约束，否则就直接采样生成响应，这部分内容我们之前讨论过

for epoch in tqdm(range(num_epochs), desc="epoch"):
    # If using KL penalty, need to get the reference model (freeze it every few epochs)
    if kl_penalty != 0:
        if epoch % compute_ref_model_period == 0:
            ref_model = model.clone()

    # Sample responses and evaluate their rewards
    responses = generate_responses(prompts=prompts, model=model, num_responses=num_responses)  # [batch trial pos]
    rewards = compute_reward(prompts=prompts, responses=responses, reward_fn=reward_fn)  # [batch trial]
    deltas = compute_deltas(rewards=rewards, mode=deltas_mode)  # [batch trial]

    if kl_penalty != 0:  # Compute under the reference model
        with torch.no_grad():
            ref_log_probs = compute_log_probs(prompts=prompts, responses=responses, model=ref_model)  # [batch trial]

    if loss_mode != "naive":  # Compute under the current model (but freeze while we do the inner steps)
        with torch.no_grad():
            old_log_probs = compute_log_probs(prompts=prompts, responses=responses, model=model)  # [batch trial]
    ...

接下来计算奖励值，然后根据你选择的算法变体来计算 delta 值，若采用 KL 惩罚项则还需在参考模型下计算对数概率，若执行裁剪操作则还需在当前模型下计算对数概率

for epoch in tqdm(range(num_epochs), desc="epoch"):
    ...
    # Take a number of steps given the responses
    for step in range(num_steps_per_epoch):
        log_probs = compute_log_probs(prompts=prompts, responses=responses, model=model)  # [batch trial]
        loss = compute_loss(log_probs=log_probs, deltas=deltas, mode=loss_mode, old_log_probs=old_log_probs)  # @inspect loss
        if kl_penalty != 0:
            loss += kl_penalty * compute_kl_penalty(log_probs=log_probs, ref_log_probs=ref_log_probs)

        # Print information
        print_information(epoch=epoch, step=step, loss=loss, prompts=prompts, rewards=rewards, responses=responses, log_probs=log_probs, deltas=deltas, out=out)
        global_step = epoch * num_steps_per_epoch + step
        records.append({"epoch": epoch, "step": global_step, "loss": loss.item(), "mean_reward": rewards.mean().item()})

        # Backprop and update parameters
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

随后根据生成的响应执行若干优化步骤，这里的核心思路在于：在生成响应后，通常需要针对这些响应执行多次梯度优化步骤，这个内循环本质上就是针对同一组响应执行多次优化步骤，为此需要计算对数概率，计算损失函数，如果需要可以加入 KL 散度惩罚项 -- 这个技巧有时有效，有时则收效甚微，然后直接进行优化即可

整体框架就是这样的：我们有一个外层迭代循环，这里暂时忽略 KL 惩罚项，因为后续还会提到一个额外的细节需要处理，这样就能生成一系列响应结果，然后快速对这些响应进行多轮迭代优化。先生成一批响应结果，然后进行若干轮迭代优化，基本思路就是这样

这里还有个关键点：如果加入 KL 惩罚项，实际上是在以参考模型为基准进行正则化，这个参考模型的更新速度甚至比外部主模型还要慢，不过这里描述的写法与 GRPO 实际算法略有差异

在实际算法实现中，其实包含三个循环结构，我们这里只用两个循环是因为参考模型的更新频率本来就比较低，而且这部分功能我们也没实现，虽然存在一些实现细节上的差异，但希望这些内容能帮助大家理解大致的实现框架

实际上你需要维护三个模型，你需要一个作为对比基准的参考模型，用于进行正则化约束，此外还需要一个冻结的旧模型，用于计算当前模型与旧模型之间的重要性比例，同时在线更新当前模型，参考模型有个比较麻烦的地方 -- 你必须完整存储整个模型副本，这会让内存占用直接翻倍

旧模型的处理方式相对好些，在代码实现时，你其实不需要复制整个旧模型，只需生成若干响应样本，预先计算并存储这些响应的对数概率即可，因为在内部循环中，你始终处理的是同一批响应数据，这样就不需要存储整个模型副本，只需保存对数概率值即可

Q & A

Q：为什么我们不直接在旧策略和最新策略之间计算 KL 散度，而非要针对参考模型来计算呢？

A ：为何选择针对参考模型而非旧策略施加 KL 惩罚，要理解这个问题，我们可以这样来看：还记得我们讨论强化学习目标函数定义的方式吗，而我们正是基于这个目标函数进行优化，这种说法其实存在一定偏差，因为实际上，我们定义这个目标函数的根本目的是为了计算梯度，我们根据计算的梯度进行参数更新，但随着训练推进，目标函数本身也会发生变化。实际上可以这样理解：在某个训练节点，我们会固定一个参考模型，然后构建出这个精心设计的目标函数，具体来说，它包含期望奖励项和 KL 散度惩罚项，如果调整过于频繁，那么改动幅度越大实际优化效果反而会偏离目标函数越远，这或许就是原因之一。说实话，从实践经验来看，梯度更新的性质决定了：根据采取的更新步数和频率，可以让新策略更接近或更偏离旧策略，实际上，我们有两种正则化机制，第一种是应用于旧策略 π old \pi_\text{old} πold 的截断机制，第二种则是针对参考策略 π ref \pi_\text{ref} πref 的 KL 散度约束。

Q ：在首次迭代中，GRPO 作用于最内层循环，初始状态下， π θ old \pi_{\theta_\text{old}} πθold 和 π θ \pi_\theta πθ 不是相等的吗？这样做是否会造成资源浪费？

A ：在首次迭代时，策略 π \pi π 等于 π θ \pi_\theta πθ，实际上你仍然会执行策略更新，你只是通过某个系数进行缩放，注意，从更新角度来看， π \pi π 始终是个常量，关键在于此时不会触发截断机制，因为比率始终为 1，因此更新操作将确保被执行，这样处理没有问题。

4.4 Experiments

接下来我们来看一些具体的实验运行结果

image_path, log_path = run_policy_gradient(num_epochs=100, num_steps_per_epoch=10, num_responses=10, deltas_mode="rewards", loss_mode="naive", reward_fn=sort_inclusion_ordering_reward, use_cache=True)  # @stepover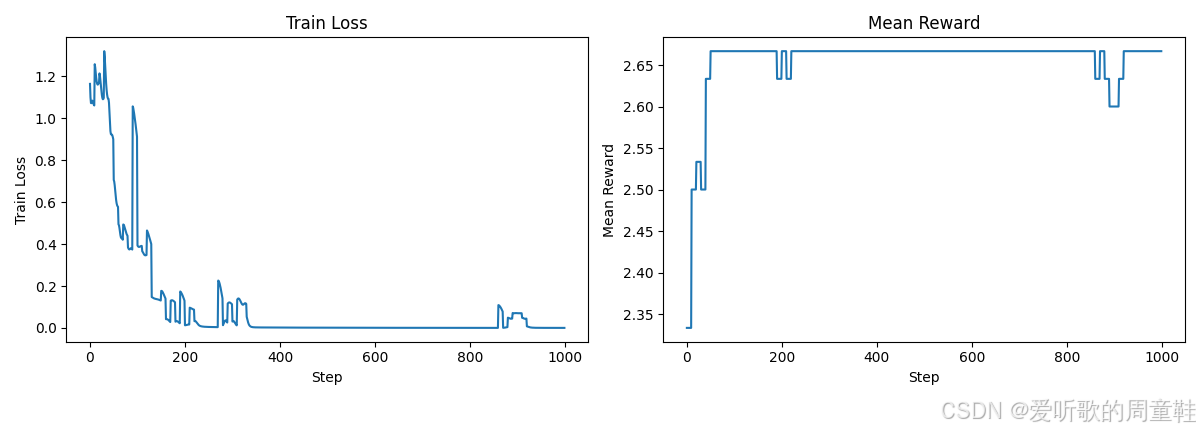

我们将进行 100 个训练周期，每个周期包含 10 个训练步数，让我们逐步解析这个实现原理

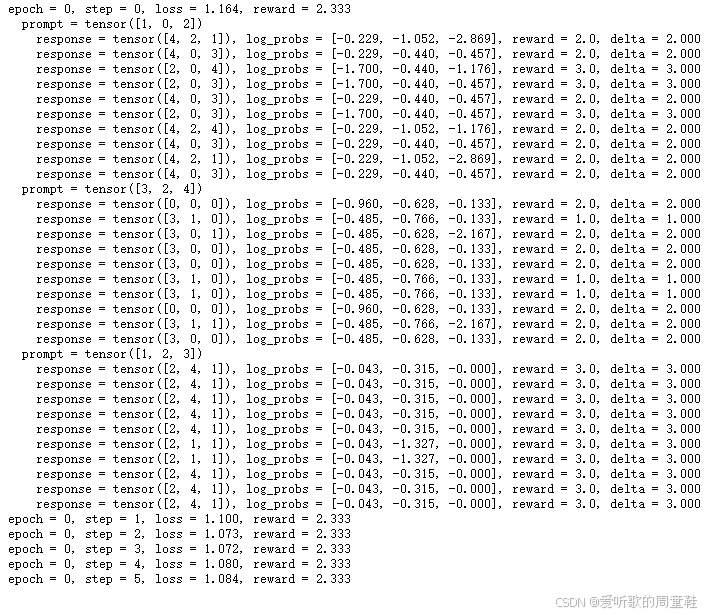
在训练初始周期（epoch 0）的第一步（step 0），模型接收到的提示是 [1, 0, 2]，模型会生成一系列响应内容，接着对这些响应进行评分，计算奖励值，然后得出差值，在这个特定情况下，该差值就等于奖励值本身，因此，相比评分为 2 的响应，我们会更倾向于向评分为 3 的响应方向进行参数更新，当再次遇到相同提示时，模型会重复这个优化过程

最终可以看到，模型输出的响应稳定获得了 3 分的奖励值，但当前效果并不理想，因为系统尚未真正将简短回答筛选出来，模型生成的数字基本都来自提示词本身，但并未实现真正的排序功能

我们来看下其他的示例表现如何：

image_path, log_path = run_policy_gradient(num_epochs=100, num_steps_per_epoch=10, num_responses=10, deltas_mode="centered_rewards", loss_mode="naive", reward_fn=sort_inclusion_ordering_reward, use_cache=True)  # @stepover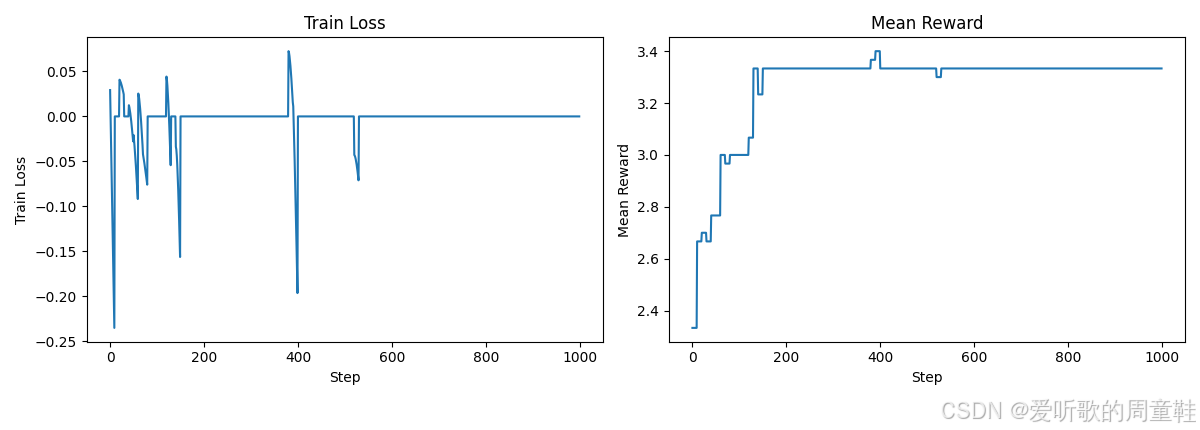

可以看到，当我们采用中心化奖励机制后，平均奖励值正在稳步提升，现在数值已经突破 3，而之前只有 2，这个进展相当不错，现在我们来分析这次运行结果

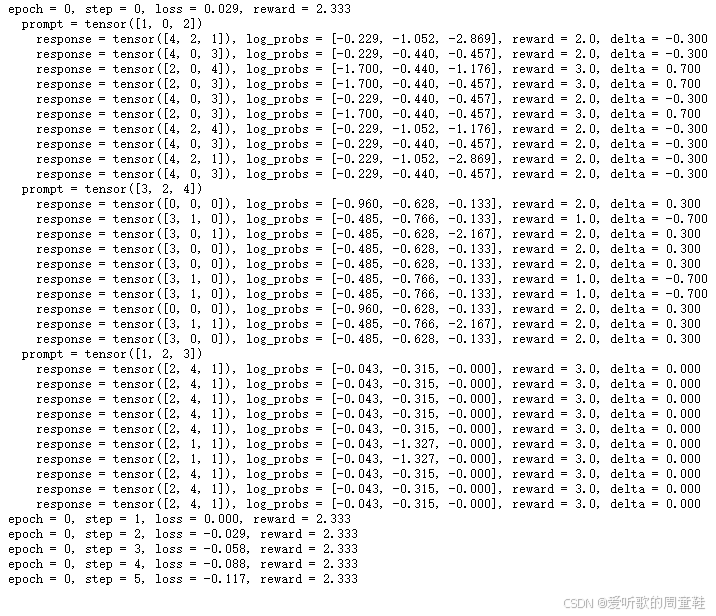
请注意，这里我们生成了一些示例，奖励值分别为 2 和 3，但由于采用了中心化处理，我们会引导模型向奖励值为 3 的样本靠拢，同时远离奖励值为 2 的样本，这就是中心化处理的作用，如果所有样本的奖励值相同，那么中心化处理实际上不会产生任何效果，而之前的更新操作现在看来并不明智，仔细想想当我们对 [1, 2, 3] 进行排序时，如果所有生成的响应质量都同样糟糕，那么基于这些数据进行更新可能并不合理

让我们最后看看这个方法的效果如何，看来效果还是不太理想，不过奖励值倒是稍微提高了一点，可能还需要对这个参数再微调一下，但至少现在能正确输出数字时，系统确实获得了奖励，0 和 1 这两个数字的排序还不算最混乱的

可以看到有些批次中所有 delta 值都归零了，因此在这个批次上继续训练其实无济于事，但如果重新生成样本，或许能得到新的数据并实现参数更新，由此可见，部分奖励机制是把双刃剑，因为我们设置了多个得分点，这是个不错的奖励机制，但问题仍未得到彻底解决，因此大家在设置额外奖励时必须格外谨慎

最后是标准化处理：

image_path, log_path = run_policy_gradient(num_epochs=100, num_steps_per_epoch=10, num_responses=10, deltas_mode="normalized_rewards", loss_mode="naive", reward_fn=sort_inclusion_ordering_reward, use_cache=True)  # @stepover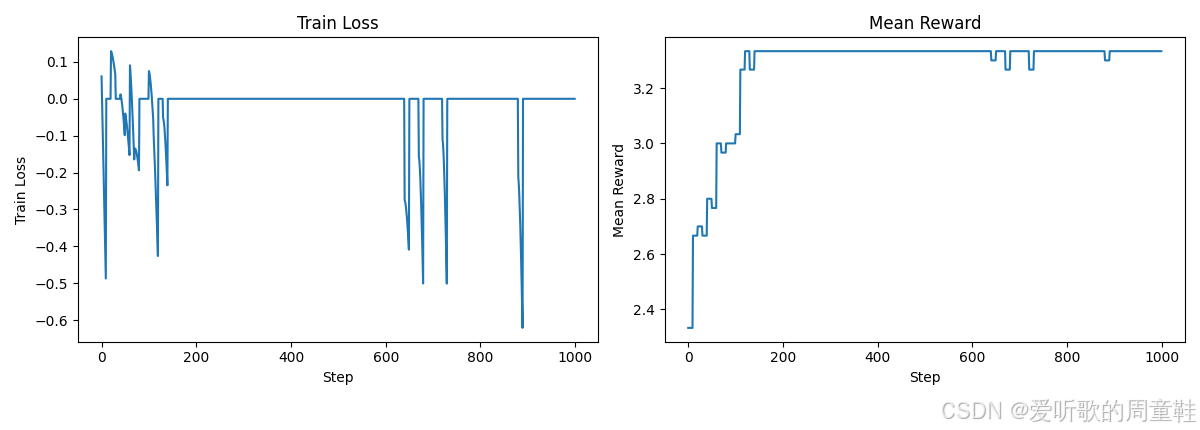

这里的归一化操作实际效果相当有限，我们就跳过这部分了，需要注意的一点是，观察这些损失曲线时你可能会想：看起来不错啊，但为什么奖励值在上升，效果却依然不尽如人意呢

这正印证了我们之前的观点：单纯追求损失最小化在这里其实是个伪命题，我们并不是在优化一个可以随时间衡量的单一损失函数，因为模型的响应集合本身就在不断变化，你实际上缺乏一个恒定的损失参考基准，你或许能在某个验证集上计算损失值，但如果只有奖励信号，那最终你只能依赖奖励机制本身

因为仔细想想，即便你有一堆样本，模型可能只是机械地生成它们而已，这就好比损失值仅仅取决于模型当前的生成内容，所以这本质上是个自我循环的闭环，因此单纯监控损失值其实没有太大意义了

5. Summary

最后，我们做个简单的总结吧

说到强化学习，它确实令人振奋，因为从某种意义上说，这可能是让模型真正超越人类能力的关键，毕竟，有监督学习只能让你模仿标注数据中呈现的行为模式。关键在于：只要能量化评估，就能优化提升，只要定义了奖励机制，正如我们在排序示例中看到的，优化过程本身就充满挑战，但关键的问题或许是：如何设计出无法被取巧破解的奖励机制以及具备泛化能力的环境框架，这确实是当前研究的热点领域

回顾策略梯度框架，这个概念本身其实非常清晰明了，写出期望奖励函数后减去基线值，本质上都是同样的操作，接下来你只需要设法估算出这个奖励值或优势函数

有件事我们之前没讨论过，但其实很重要，那就是强化学习系统，构建强化学习系统并实现规模化实际上比预训练要复杂得多得多，原因在于你必须进行推理，而推理本身就是个极其棘手的问题，你还得同时管理多个模型，比如你有训练的策略模型，如果采用 PPO 算法还需要价值评估模型，如果涉及推理环节，比如部署了推理工作节点，你就得把模型传输过去才能执行推理，若采用智能体环境，还需要启动并运行这个环境本身

除此之外，你还得维护旧策略和参考策略，这意味着你需要同时维护多个模型，更复杂的是，所有组件都必须实现并行分布式协同工作，让整个系统流畅高效地运转起来，这里涉及的工作量相当庞大

OK，以上就是本次讲座的全部内容了

结语

本讲我们主要讲解了 结果奖励（outcome-based）强化学习在语言模型中的形式化推导与方差控制方法，内容围绕策略梯度在 LLM 场景下的具体建模展开，重点分析了基线（baseline）、优势函数（advantage）以及分组相对比较（group-relative）在降低训练噪声中的核心作用。

我们首先从语言模型生成过程出发，将其形式化为一个极简的强化学习问题：状态由 prompt 与已生成 token 构成，动作是下一个 token 的选择，而奖励仅在完整序列生成结束后给出。这一设定说明，LLM 中的 RL 更接近 "可控动力学下的结果优化"，但也天然面临 奖励稀疏与梯度方差过大 的问题。

我们随后系统推导了策略梯度的标准形式，并指出直接使用回报 R 进行更新会导致训练极不稳定。为此引入 基线（baseline） 作为控制变量，在不改变期望梯度的前提下降低方差，并给出了最优基线的解析形式，从而自然过渡到 优势函数（Advantage） 的视角。

在此基础上，我们进一步解释了 组内相对化（group-relative）思想 的来源：当同一 prompt 下采样多条回答时，可以利用组内奖励的均值或归一化结果作为隐式基线，仅学习 "相对更好" 的输出。这一思路在数学上等价于优势函数的近似实现，是 GRPO 等方法能够稳定工作的关键原因。

最后，我们通过一个可运行的简单任务数字排序完整串联了实现细节，包括奖励构造、相对差分、旧策略冻结与 log-prob 比值计算，重点强调在 LLM 强化学习中，真正决定成败的不是奖励函数多复杂，而是是否正确地控制了更新方差并保持策略稳定性。

整个讲解非常通俗易懂，大家感兴趣的可以看看

这是本系列课程的最后一讲了，剩下的就是需要大家去完成每个章节对应的作业了🤗

这是博主 2025 年度的最后一篇文章了，感谢大家长期以来的关注，我们 2026 年见，最后提前祝大家新年快乐🎉🎉🎉

参考

• https://stanford-cs336.github.io/spring2025
• https://www.youtube.com/playlist?list=PLoROMvodv4rOY23Y0BoGoBGgQ1zmU_MT_
• https://github.com/stanford-cs336/spring2025-lectures
• https://stanford-cs336.github.io/spring2025-lectures/?trace=var/traces/lecture_17.json