射频网课学习第七章(驱动放大器设计)

今天我们来学习第七部分。在这一部分，我们将运用前面所学的理论知识，来设计一个小信号放大器 的实例。这个小信号放大器通常指驱动放大器 。

一般来说，驱动放大器的设计目标相对明确：主要考量是提供足够高的增益 以及实现良好的输入输出匹配。这就是设计驱动放大器最主要的两个方面。

明确设计规格

现在，我们来看看这个设计具体会运用到哪些理论。我们先为这个驱动放大器的设计实例设定一些规格参数：

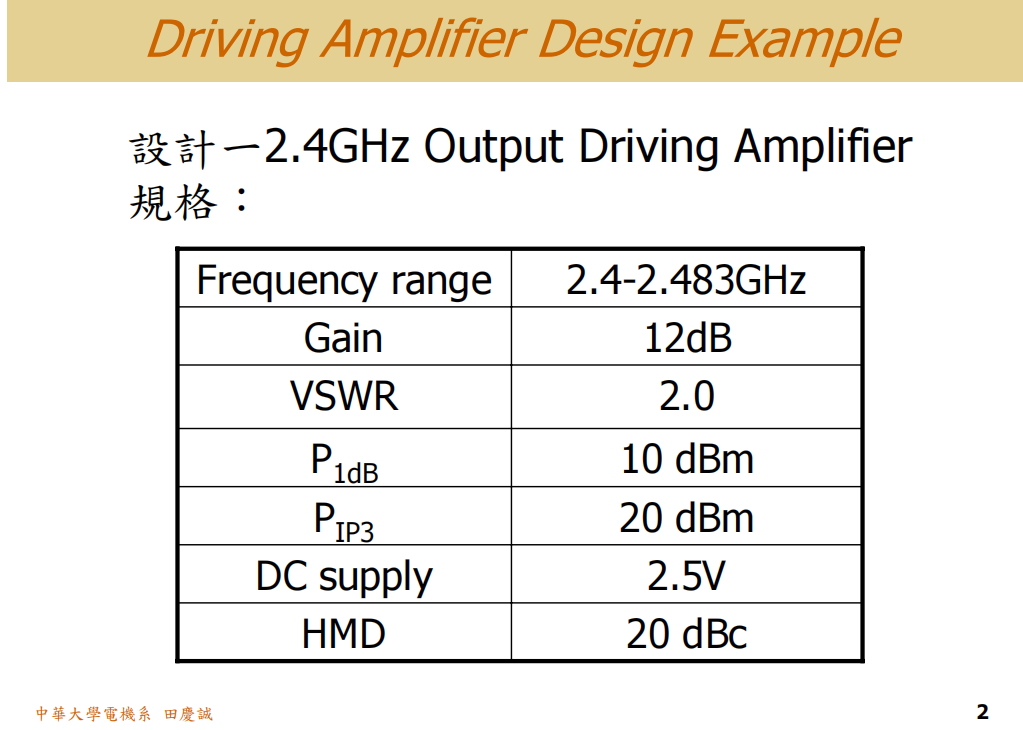
工作频率 ：设定在 2.4 GHz。
应用场景 ：这是一个用于驱动功率放大器的前置放大器 。以常见的2.4 GHz应用为例，末级功率放大器的输出功率通常在 20 dBm 左右。因此，驱动级的输出功率需要达到约 10 dBm。
增益需求 ：考虑到前级芯片的输出功率通常在 -5 dBm 到 0 dBm 之间，为了将信号提升到 10 dBm，驱动放大器所需的增益大约在 10 dB 到 15 dB 之间。
具体规格 ：
- 频率范围：2.4 GHz -- 2.483 GHz（带宽83 MHz，符合美规标准）。
- 增益：目标设定为 12 dB。
- 输入/输出匹配 ：VSWR 要求 ≤ 2.0（即反射系数 ΓΓΓ ≤ 1/3）。
- 输出功率 ：P1dBP_{1dB}P1dB 最大输出功率希望达到 10 dBm 左右。
- 线性度 ：PIP3P_{IP3}PIP3 通常比P1dBP_{1dB}P1dB高约 10 dB，因此目标设为 20 dBm。
- 工作电压(DC supply) ：采用两颗锂电池供电，电压范围为 2.5V。
- 谐波抑制(HMD) ：由于输出将驱动PA，必须严格控制谐波。要求二次谐波（在4.8 GHz）的功率至少要比主频（2.4 GHz）信号低 20 dBc。

根据以上规格，我们开始进行设计。

第一步：选择合适的晶体管。

输出功率(Output power)

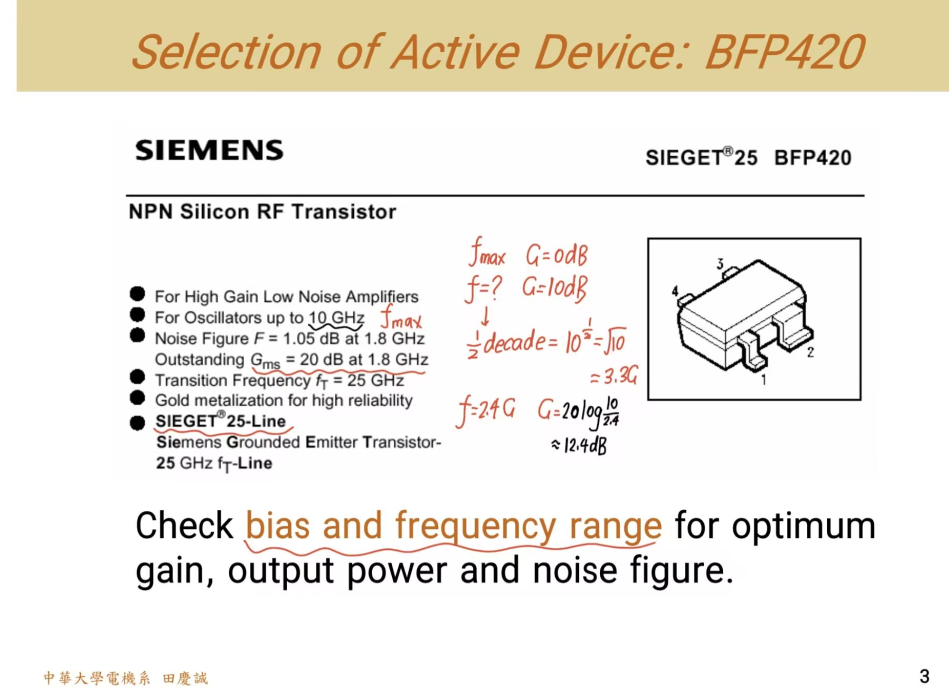
我们继续以 BFP420 晶体管为例进行分析。这款晶体管其实很适合1.8 GHz的应用，对于2.4 GHz频段也是可行的选择。它的特征频率(transition frequency) fTf_TfT 为 25 GHz。根据经验，晶体管在fTf_TfT/10（即2.5 GHz）的频率下通常仍能保持良好的性能。

从它的参数来看，其振荡频率可达 10 GHz(for oscillators up to 10GHz)（这接近其 fmaxf_{max}fmax）。我们可以快速估算一下它在2.4 GHz下的增益：增益随频率的下降斜率通常是每十倍频程 20 dB。已知在 10 GHz 时增益约为 0 dB，那么通过计算 10 GHz 与 2.4 GHz 的比值，并换算成对数关系，可以估算出在 2.4 GHz 时其潜在增益仍有约十几dB(12.4dB)，符合我们的需求。

此外，数据手册显示其在 1.8 GHz 时的最大稳定增益可达约 20 dB(Outstanding Gms=20dBG_{ms} = 20dBGms=20dB)，这进一步证实了其可用性。

接下来我们来进一步分析一下晶体管BFP420的相关规格。

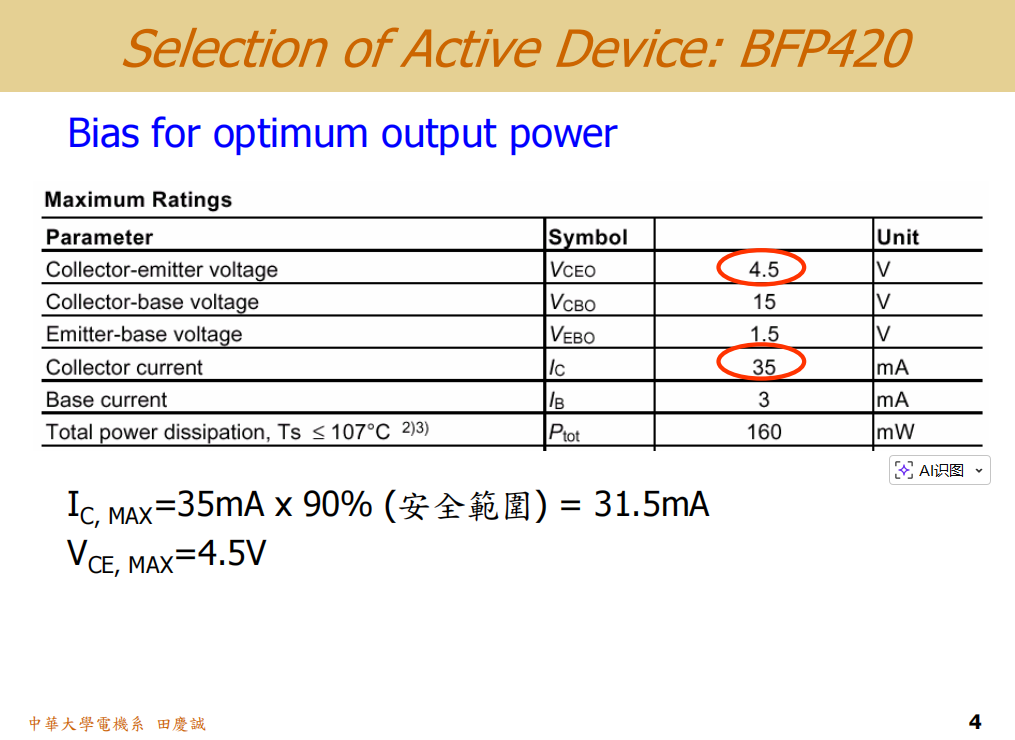
数据手册中给出了两个关键参数：VceoV_{ceo}Vceo最大耐受电压为4.5V ，IcI_cIc最大耐受电流为35mA。根据这两个值，我们可以得出以下信息：

安全工作电流 ：为避免烧毁，实际工作电流不应超过最大值的90%，即 31.5mA 是较为安全的范围。
最大输出功率估算 ：有了最大电压和电流，我们可以估算晶体管理论上能输出的最大功率。首先，我们需要确定晶体管的直流工作点（Q点）。从直流IV曲线（蓝色线）可以看出：

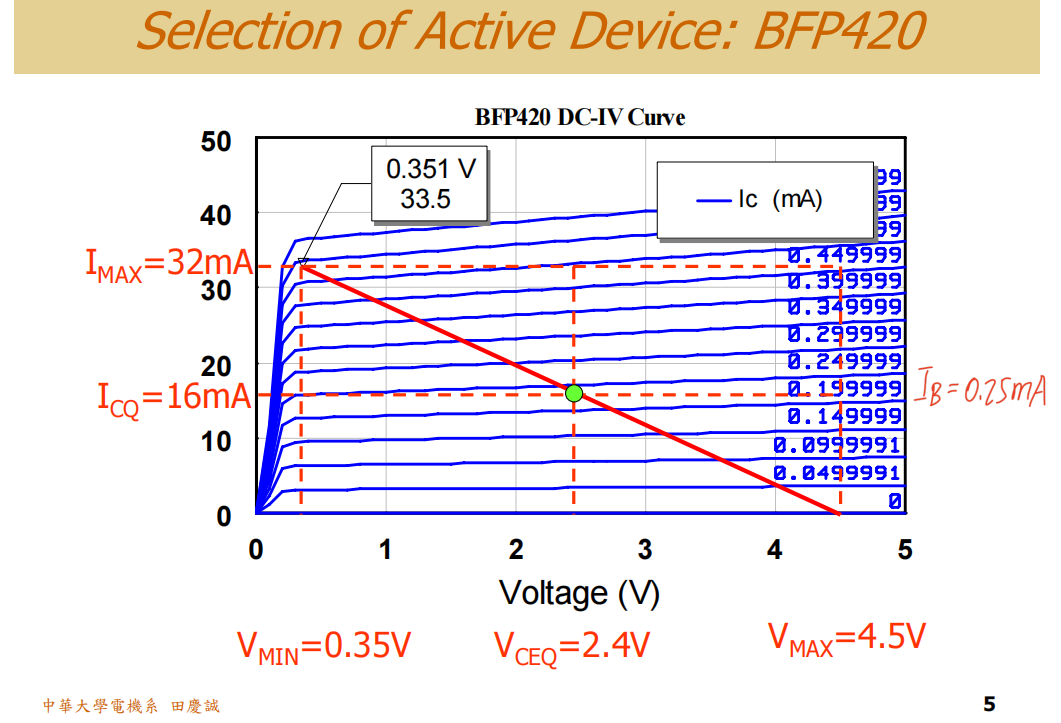
有效工作电压范围大约从0.35V(Vmin)(V_{min})(Vmin)开始，最高到4.5V(Vmax)(V_{max})(Vmax)
安全电流范围最高到32mA(31.5mA)。
A类放大 的理想偏置电流是最大安全电流的一半，即 16mA。
A类放大 的理想偏置电压是最高和最低工作电压的平均值，即 (4.5V + 0.35V) / 2 ≈ 2.4V。

我们设计的供电电压是2.5V，为集电极电阻留下约0.1V的压降，因此2.4V的偏置电压是可行的。如果算出的偏置电压高于供电电压，设计就必须调整。

基于这个Q点（16mA, 2.4V），我们可以计算其理论最大输出功率（P1dBP_{1dB}P1dB的近似估算公式：Pmax≈(ICQ∗(VCEQ−Vmin))/2P_{max} ≈ (I_{CQ} * (V_{CEQ} - V_{min})) / 2Pmax≈(ICQ∗(VCEQ−Vmin))/2）。其中，ICQI_{CQ}ICQ取16mA，VCEQV_{CEQ}VCEQ(集电极电压单边的最大理想摆幅)取(4.5V + 0.35V)/2 ≈ 2.4V，计算得到功率约为 16.4mW ，即 12.15dBm 。

这与我们驱动放大器输出 10dBm 的目标基本吻合，说明从功率容量上看，该晶体管是合适的。

但要获得这个最大输出功率，需要一个特定的最佳负载阻抗 。根据负载线分析法，这个最佳负载 Ropt=ΔV/ΔI=(4.5V−0.35V)/0.032A≈128ΩR_{opt} = ΔV / ΔI = (4.5V - 0.35V) / 0.032A ≈ 128ΩRopt=ΔV/ΔI=(4.5V−0.35V)/0.032A≈128Ω。也就是说，只有当输出端"看到"128Ω的负载时，才能达到12.15dBm的输出。然而，驱动放大器的设计核心是增益和匹配，通常不会刻意去实现这个最佳功率负载。在实际的输入输出匹配设计中，负载阻抗往往偏离128Ω，因此实际输出功率会低于理论最大值，很容易掉到10dBm以下。这是设计时需要特别注意的。

输出功率(Output power)

接下来，我们检查晶体管的增益是否满足要求。

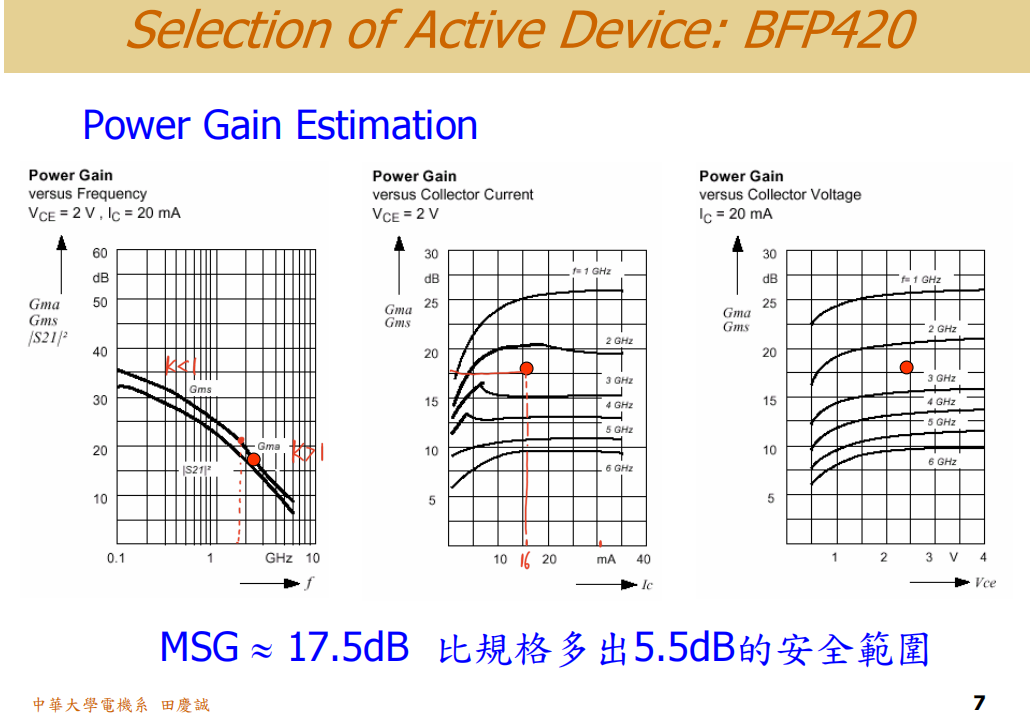
查看最大稳定增益（GmsG_{ms}Gms）曲线(左边图)，可以发现在频率接近 2GHz 时，稳定因子K从小于1转变为大于1（曲线上的明显转折点）。当K>1后，我们应关注最大可用功率增益（GmaG_{ma}Gma）。

在 2.4GHz 频率下：

从GmaG_{ma}Gma曲线来看，在16mA的偏置电流下，增益大约为 17.5dB ~ 18dB(中间图)。
从S21S_{21}S21参数曲线（左边图）来看，增益也大约在 17dB 左右。
同时，在Vce=2.4VV_{ce}=2.4VVce=2.4V的偏置条件下(右边图)，其增益也大致落在这个范围。

这三方面信息都确认了，在该偏置点下，晶体管在2.4GHz能提供约 17dB 的增益，满足我们12dB的需求。

然后，我们评估噪声性能。

在选定的工作点（Ic=16mA,f=2.4GHzI_c=16mA, f=2.4GHzIc=16mA,f=2.4GHz）处，从噪声系数曲线上查得对应的噪声系数约为 1.5dB。这个值已经相当不错。虽然继续降低电流（例如到6mA）可以将噪声系数降至最低约1.25dB，但这会严重牺牲输出功率能力。因此，为了兼顾输出功率，选择16mA偏置和1.5dB的噪声系数是一个合理的折中。

总结偏置点选择 ：

我们最终确定的直流工作点（Q点）为：

VceqV{ceq}Vceq = 2.4V
IcqI_{cq}Icq = 16mA
预期增益：~17dB
噪声系数：~1.5dB
理论最大输出功率：~12dBm（实际匹配后可能略低）

最后，为了进行后续的偏置电路设计，我们需要获取晶体管的电流增益（β或hFEβ或h_{FE}β或hFE）和基极-发射极导通电压（VbeV_{be}Vbe）。

电流增益 β ：从直流IV曲线可知，当Ic=16mAI_c=16mAIc=16mA时，对应的基极电流IbI_bIb约为0.25mA。因此，β=Ic/Ib=16mA/0.25mA=64β = I_c / I_b = 16mA / 0.25mA = 64β=Ic/Ib=16mA/0.25mA=64。

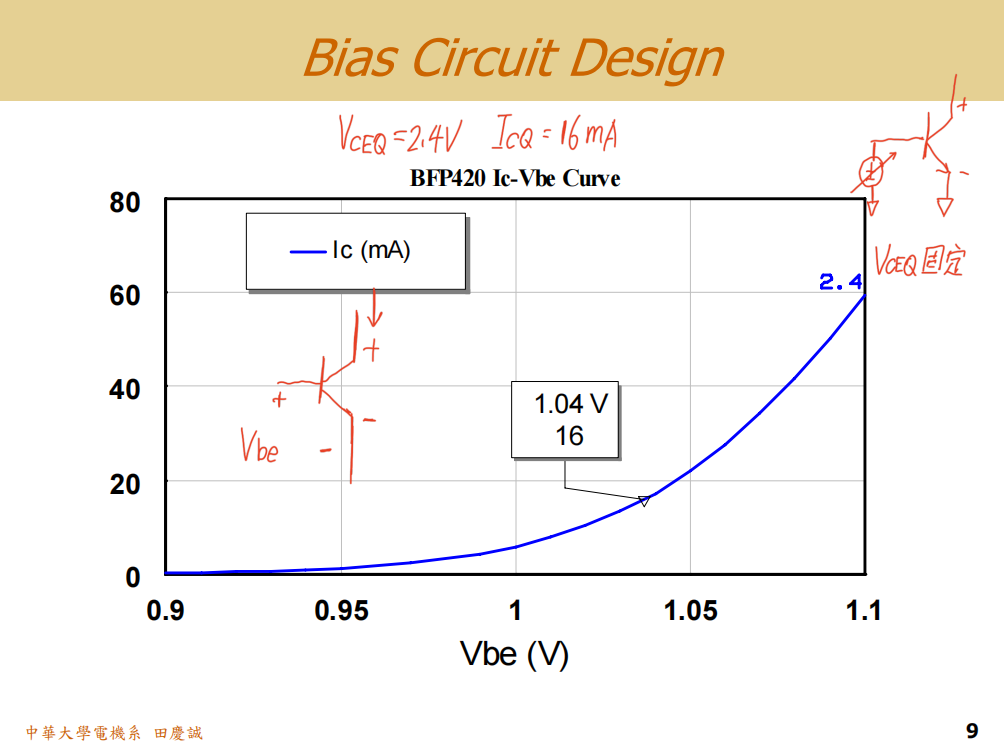
基极导通电压 Vbe ：这不是一个固定值（如常说的0.7V） ，它随工艺和偏置点变化。要获得精确值，需要通过仿真软件扫描VbeV_{be}Vbe（同时固定Vce=2.4VV_{ce}=2.4VVce=2.4V），并测量对应的IcI_cIc，从而绘制出Vbe-Ic曲线。从我们已有的特性曲线中，可以推断在该工作点下，VbeV_{be}Vbe大约在 0.9V 左右（具体数值需要通过所述仿真方法精确确定）。掌握准确的Vbe对设计稳定的基极偏置网络至关重要。

设计偏压电路

至此，我们有了设计偏置电路所需的全部直流参数：

VceqV_{ceq}Vceq = 2.4V
IcqI_{cq}Icq= 16mA
VbeV_{be}Vbe = 1.04V
β(hFE)β (h_{FE})β(hFE) ≈ 64
IbI_bIb ≈ 0.25mA

现在，我们来根据选定的工作点进行偏置电路的设计和稳定性分析。
第一步：计算偏置电路电阻值

我们采用经典的电压负反馈型偏置电路，如下图所示：

根据基尔霍夫电压定律和欧姆定律，我们可以进行计算：

集电极电阻 (Rc) ：已知电源电压VccV_{cc}Vcc=2.5V，集电极目标电压VceV_{ce}Vce=2.4V，集电极电流IcI_cIc=16mA。因此，RcR_cRc上的压降为0.1V。计算得 RcR_cRc = 0.1V / 16mA = 6.25Ω。
- 注意：6.25Ω是一个非标称值，且阻值很小。在实际选型中，我们需要选择最接近的、能采购到的标准电阻值，例如 6.2Ω 或 6.8Ω。
基极下偏置电阻 (R3) ：流经R2的电流通常设定为集电极电流的十分之一，以确保基极电压稳定。即 IR3≈16mA/10=1.6mAI_{R3} ≈ 16mA / 10 = 1.6mAIR3≈16mA/10=1.6mA。
- R2两端的电压为VbeV_{be}Vbe = 1.04V。计算得 R3 = 1.04V / 1.6mA = 650Ω。
- 该电阻一般要大于500Ω。
基极上偏置电阻 (R2) ：流经R1的电流等于IR3I_{R3}IR3与IbI_bIb之和，即 1.6mA + 0.25mA = 1.85mA。
- R1两端的电压为 Vcc - Vbe = 2.5V - 1.04V = 1.46V。
- 计算得 R1 = 1.46V / 1.85mA ≈ 789.1Ω。
- 选择标准阻值，例如 800Ω。

关键提醒：元件选型

标准值：电阻、电容、电感都有标准系列（如E24系列）。设计中必须使用这些标准值，否则无法采购或生产。
电阻精度：一般设计中，5%精度的电阻（E24系列）已足够。高精度设计才会用到1%精度（E96或E192系列）的电阻。
仿真优化：以上计算值为理论估算。在实际电路仿真中，通常需要微调R1或R2的阻值，以使工作点（Ic, Vce）精确落在目标值上。

第二步：封装模型与稳定性初始分析

在进行小信号分析前，必须将晶体管的封装寄生参数（Package Model）纳入考虑。忽略这些寄生效应（尤其是引线电感），仿真结果将与实际性能严重不符。

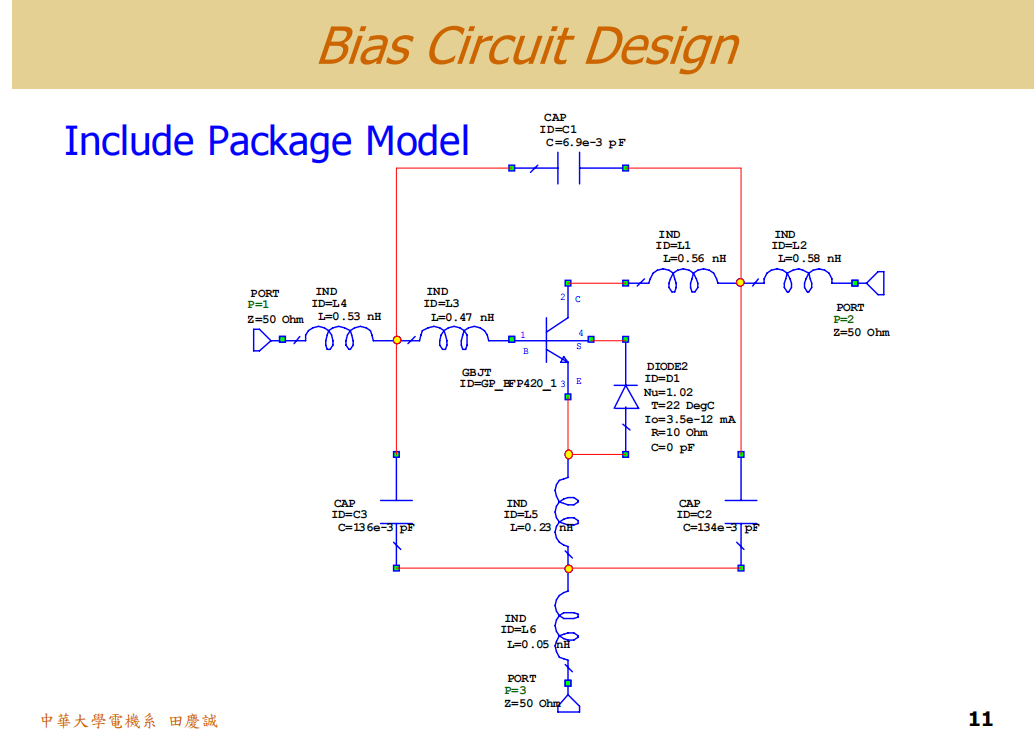
建立好包含封装模型的晶体管子电路后，我们首先进行稳定性分析。我们暂时使用一个理想的大电感（如1H）作为射频扼流圈，使其在射频频段视为开路。

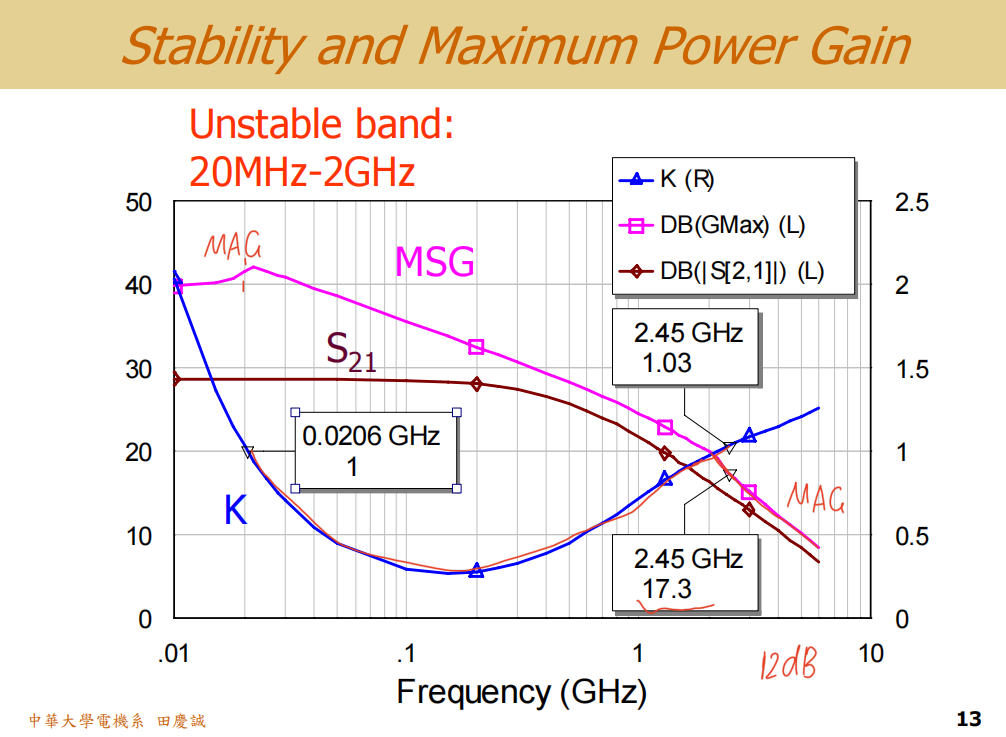
分析S参数和稳定性因子K，我们发现：

在目标频率 2.45GHz 附近，K > 1，且最大可用增益（GmaG_{ma}Gma）约为 17.3dB。这与我们之前从数据手册预估的17dB相符。
然而，在低频段（约20MHz至2GHz） ，K值小于1，电路潜在不稳定，可能发生低频振荡。这是许多射频放大器设计的通病，必须予以解决。

第三步：设计稳定性网络

我们的目标是：在目标频段（2.45GHz）保持高增益，同时在低频段引入损耗以提升稳定性。

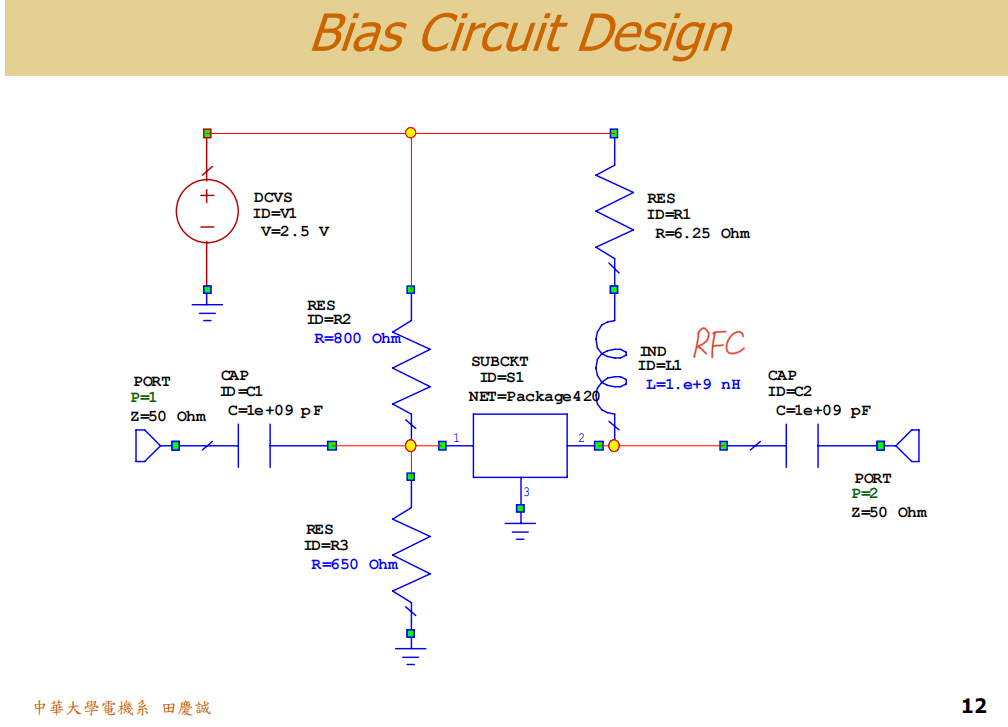
方法是将射频扼流圈（RFC）的电感值从"理想开路"状态减小到一个有限值。这样，在低频时，电感阻抗较低，部分射频信号会"看到"并流经基极偏置电阻R1和R2，从而被消耗掉，提升K值。

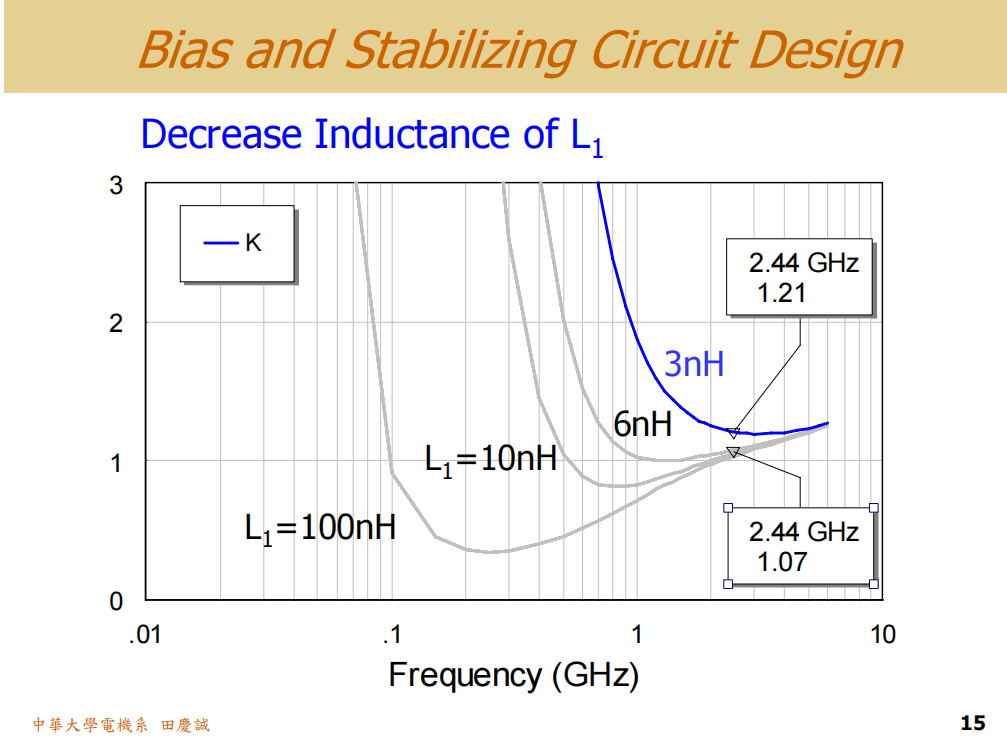
我们通过扫描电感值来观察效果：

当电感为 100nH 时，不稳定频段（K<1）从约500MHz延伸至2GHz以上。
当电感减小到 10nH 时，不稳定频段的范围开始缩小。
我们继续优化，发现当电感值约为 6nH 时，可以在整个频段（从DC开始）实现K > 1，即无条件稳定。同时，这个电感值在2.45GHz时的感抗足够高，对目标频段的增益影响很小。

将扼流圈电感值调整到 6nH 时，我们发现稳定性因子 K 在整个频段都大于 1，达到了无条件稳定。此时，在 2.4GHz 处的增益仍有约 17dB。

然而，我们的目标增益仅为 12dB，有 5dB 的裕量。为了进一步提升电路在目标频段的稳定性（K值），我们可以将电感值进一步减小至 3nH。这样，即使在 2.4GHz，信号也能部分"看到"偏置电阻，从而引入少量损耗，降低增益，同时提升K值。

采用 3nH 电感后，我们重新仿真包含整个偏置和稳定性网络的电路。其 S 参数（粉色曲线）显示：

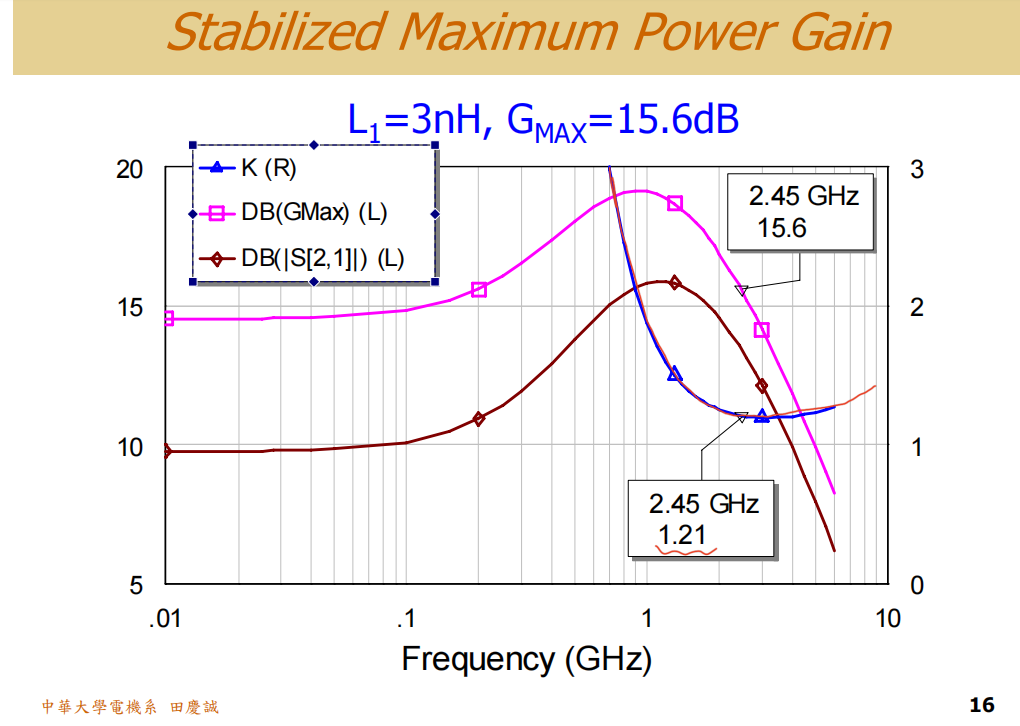
在 2.4GHz 处，最大可用增益从 17dB 下降到了约 15.6dB。
此时的稳定性因子 K 值约为 1.21，电路非常稳健。

至此，我们的偏置电路和稳定性网络设计完毕。关键是要检查 K 值曲线，确保在整个感兴趣的频段内 K > 1，防止潜在振荡。

输入输出匹配网络设计

电路稳定后，开始设计匹配网络以实现最大功率传输和 50Ω 接口匹配。

确定最佳反射系数 ：
- 实现最大增益（GmaxG_{max}Gmax=15.6dB）时，晶体管需要特定的源反射系数 ΓMSΓ_{MS}ΓMS 和负载反射系数 ΓMLΓ_{ML}ΓML。
- 通过仿真软件的计算或图解方法（绘制等增益圆），我们得到：ΓMSΓ_{MS}ΓMS = 0.605 ∠ -173° ，ΓMLΓ_{ML}ΓML也有相应的复数结果(0.416 ∠ -65.8°)。

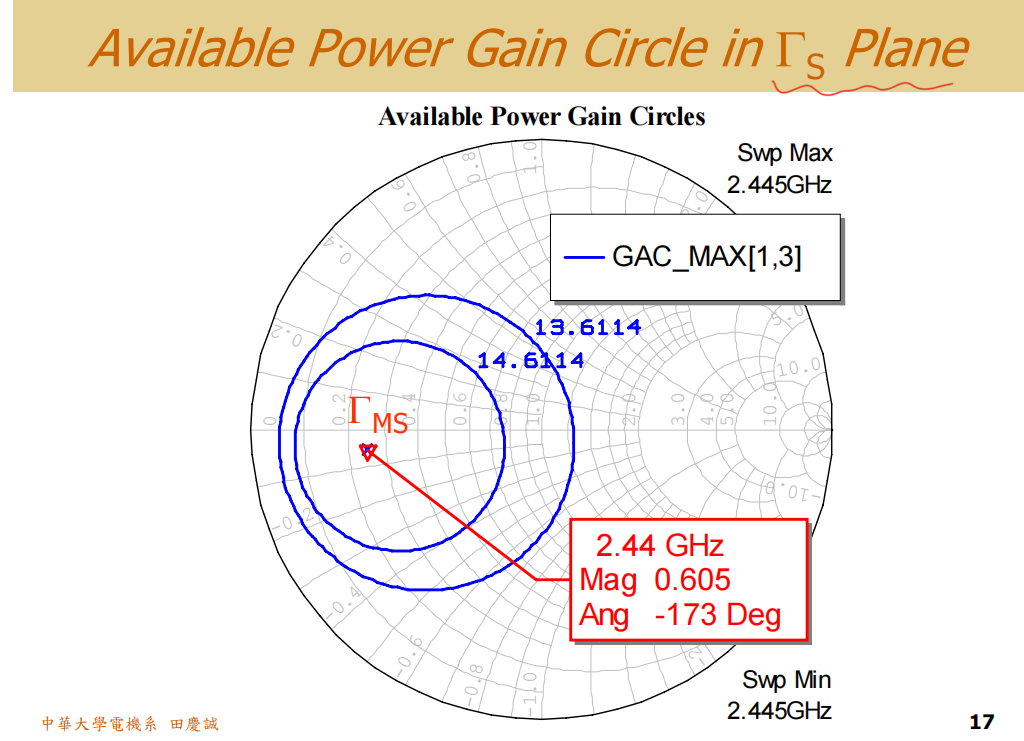
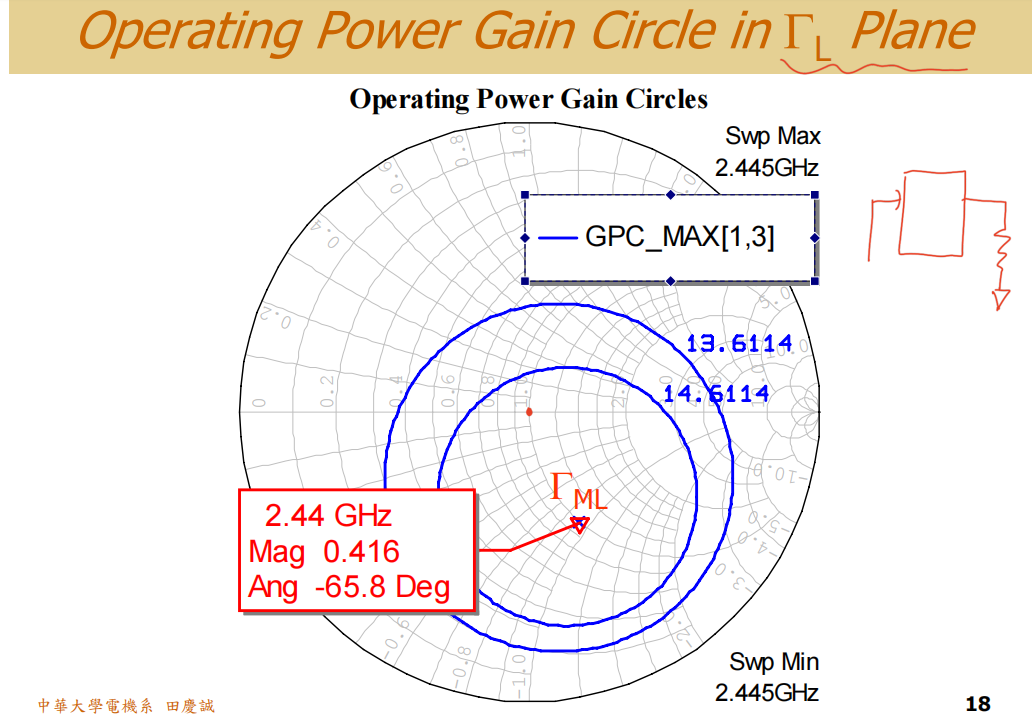
最后图解的结果如下:

错误方法：先设计输入匹配，让 S11 变好，然后发现 S22 变差了；再去调输出匹配，结果 S11 又变差......陷入无限循环。

正确方法（"系统求解"）：利用仿真软件，直接对包含了所有元件的完整二端口网络进行求解，一次性计算出实现 Gmax 所需的 Γ_MS 和 Γ_ML。然后分别独立地**设计输入和输出匹配网络，将它们匹配到50Ω。这样就能一次成功，避免反复折腾

设计输入匹配网络：

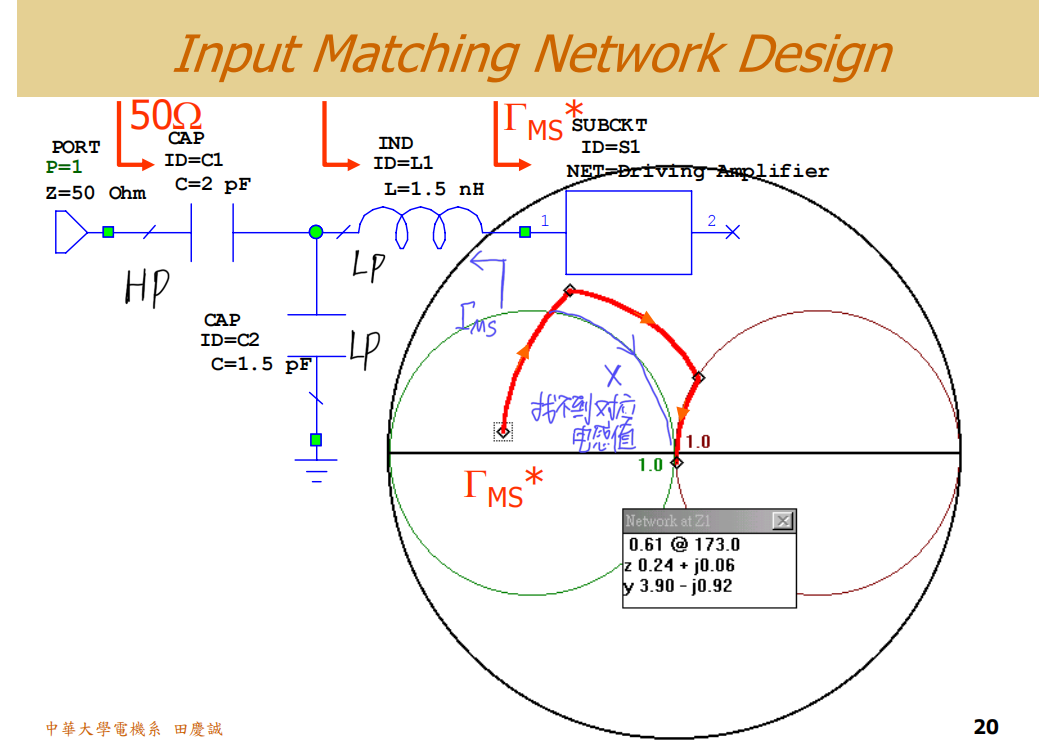
目标：将 50Ω 源阻抗变换为ΓMSΓ_{MS}ΓMS。
方法：在史密斯圆图上，从 50Ω 点（中心）开始，通过添加无源元件，将阻抗匹配到ΓMSΓ_{MS}ΓMS点。
关键：使用标准元件值 ！软件初始给出的匹配值（如 2.05pF， 2.27pF）往往是理想值，实际中不存在。我们必须调整匹配网络的拓扑结构，直到电感、电容值变为可采购的标准值（如 1.5pF， 2pF）。
拓扑选择 ：这里采用了"LCL"结构（串联L -> 并联C -> 串联L）。这不仅仅是一个匹配网络：

* 它是一个低通滤波器 ，有助于抑制高频谐波和杂散。

* 相比简单LC结构，它提供了更多设计自由度，更容易凑出标准元件值。

设计输出匹配网络（一个错误示范） ：

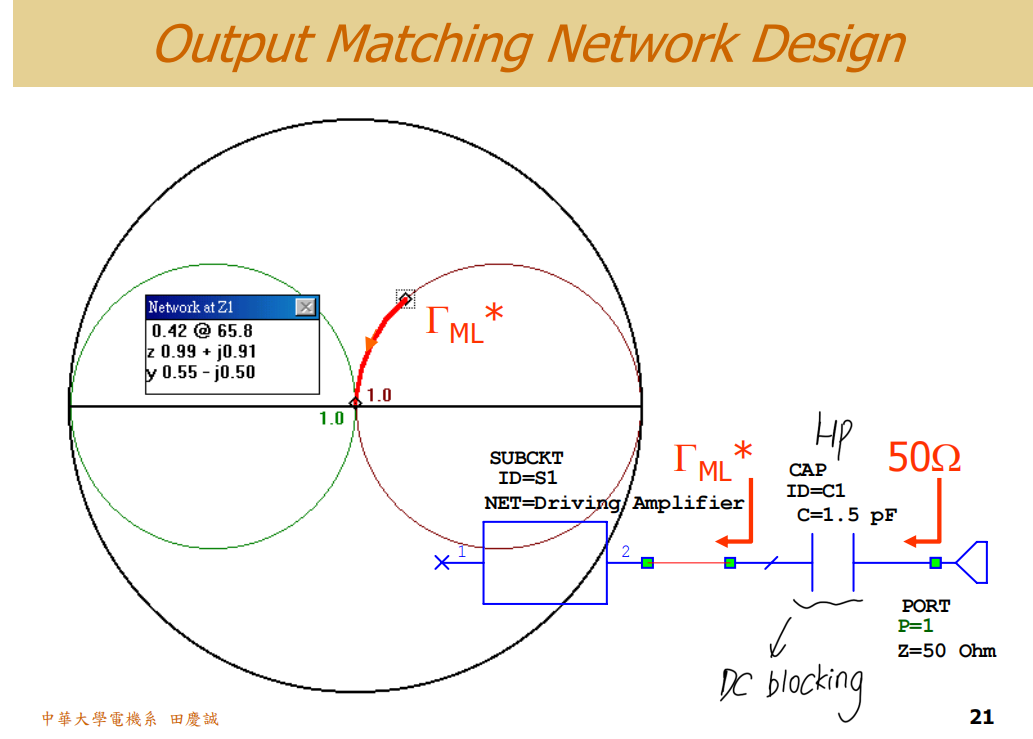
为了演示常见错误，我最初设计了一个极其简单的输出匹配：仅仅使用一个串联电容 。
问题分析 ：这是一个高通型网络 。对于功率放大器而言，输出级是谐波含量最高的地方。这种高通结构对谐波（尤其是二次谐波 4.8GHz）几乎没有抑制能力，完全违背了我们 -20dBc 的谐波抑制指标。如果这样设计，谐波能量将畅通无阻地辐射出去，导致电磁兼容（EMC）测试失败。

因此，输出匹配必须采用低通或带通结构，在实现基波匹配的同时，天然地抑制高频谐波，而这个直接设计的问题，我们将在后面看到它带来的后果，现在我们暂时先这样设计。

潜在问题

刚才我们偷懒，在输出端只用了一个高通元件（串联电容）做匹配。这在实际中，尤其是功率放大器中，是绝对错误 的。输出谐波必须用低通或带通网络来抑制。

然而，设计中最致命的问题往往不在核心匹配电路，而在看似简单的偏置和电源部分。

一、电源不是地

在仿真里，我们轻松地把偏置点"接地"。但在实际PCB上：

电源线不是射频地：你接上的电源线或连接器，对射频信号来说是一段未知长度的传输线，其阻抗特性完全未知。
必然振荡：如果没有妥善处理，射频信号会通过偏置路径形成反馈环路，100%会导致电路振荡。

解决方案：必须添加退耦电容！

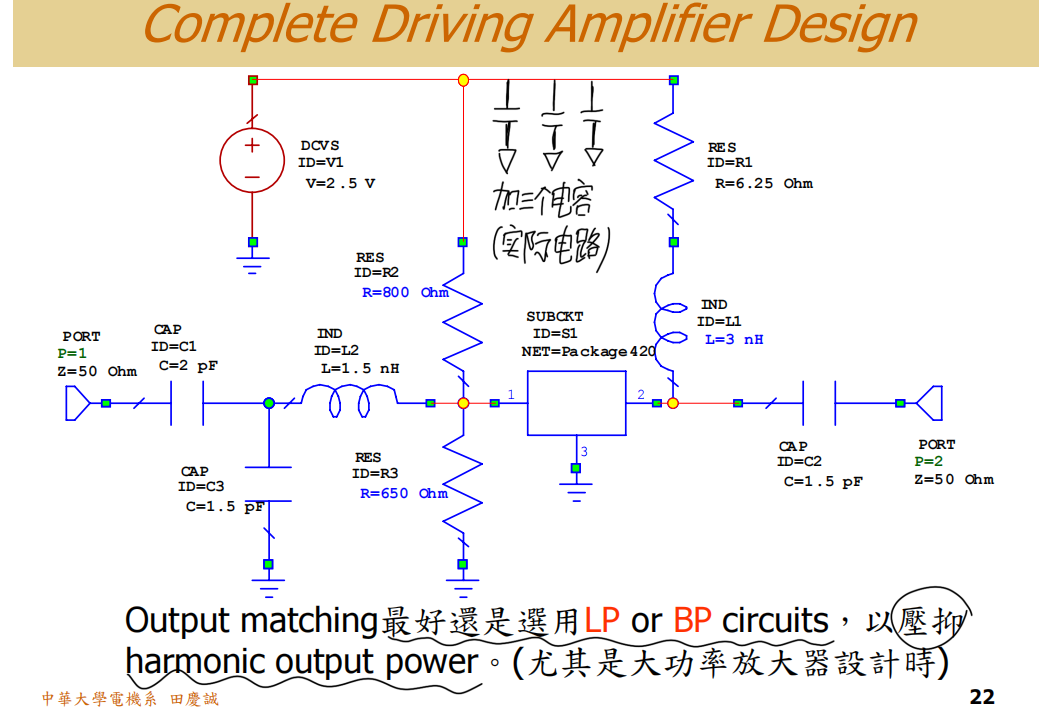
在偏置网络的供电接入点，必须并联一组不同容值的退耦电容（例如：10μF、0.1μF、10pF）。它们的作用是为不同频段的射频信号提供到地的低阻抗通路，防止信号沿电源线乱窜。

二、真实案例

一位学长的功率放大器（PA）设计遇到了更复杂的问题：

电源噪声：电路板环境噪声大，低频噪声通过长走线的电源网络窜入。
扼流圈失效：他使用的3nH扼流圈对低频噪声阻抗很低，挡不住。
初次改善 ：在电源入口串联磁珠（Bead） ，成功抑制了低频噪声。磁珠在特定频率（如100MHz）谐振，呈现高阻抗。
新问题爆发：更换了更小尺寸（成本更低）的PA芯片后，测试时谐波（4.8G， 7.2G， 9G）全部超标。
根源分析 ：
- 磁珠仅对谐振点附近的低频有效。对于9GHz高频谐波，磁珠相当于一个小电容，阻抗极低，完全无法阻挡。
- 新的PA芯片内部防护可能更差，谐波更易从偏置引脚泄漏。
- 谐波能量通过磁珠（已失效）和电源线辐射到整个电路板，形成干扰。

三、如何围剿杂散能量

这个案例的核心教训是：不希望出去的能量，必须在系统内部消耗掉。

分频段治理 ：
- 低频段 ：使用大电容+磁珠组合，提供低阻抗通路和吸收。
- 高频/谐波段 ：磁珠已无效。需要在靠近芯片偏置脚的地方，串联一个小电感（如几nH的射频扼流圈），对高频形成高阻抗。
关键技巧：为高频能量提供"泄放路径" 。
- 仅靠电感把能量"弹回去"，能量还在系统里，会找其他路径辐射。
- 更有效的方法是：在电感后面（靠近电源端），并联一个到地的射频电阻 （如几十欧姆）。这样，高频谐波能量会选择走这条路径，被电阻吸收并转化为热能消耗掉，而不会继续向后传导或辐射。
- 对于直流偏置电流，这个电阻的阻值要足够大，以免造成过大压降。

结论：偏置/电源网络的设计，其复杂性和重要性远超核心电路匹配。它需要你：

理解实际元件（磁珠、电容、电感）的全频段特性。
建立 "分频段治理" 和 "能量泄放" 的设计思维。
通过反复的调试和失败积累经验。

全面验证

好，现在我们已经完成了全部的设计，现在就是验证它的性能是否达到我们的目标要求。

一个完整的设计，必须通过仿真给出以下几张关键图，用于性能评估和问题调试：

S参数：检查增益、匹配和稳定性。
谐波仿真图：明确显示基波、二次、三次谐波功率，验证是否满足抑制指标。
功率仿真 ：得到1dB压缩点（P1dBP_{1dB}P1dB）和三阶交调点（IP3）。
负载牵引（Load Pull）等值线图：这是调试的"地图"。它能直观展示负载阻抗如何影响输出功率、增益和效率。当性能不达标时，你可以根据这张图判断该调整输出匹配（改变负载阻抗）还是输入匹配。

S参数

首先，这是我们设计的放大器最终的小信号S参数 仿真图。可以看到，在2.4GHz到2.48GHz的目标频段内，增益曲线（S21）左右比较对称、平坦。

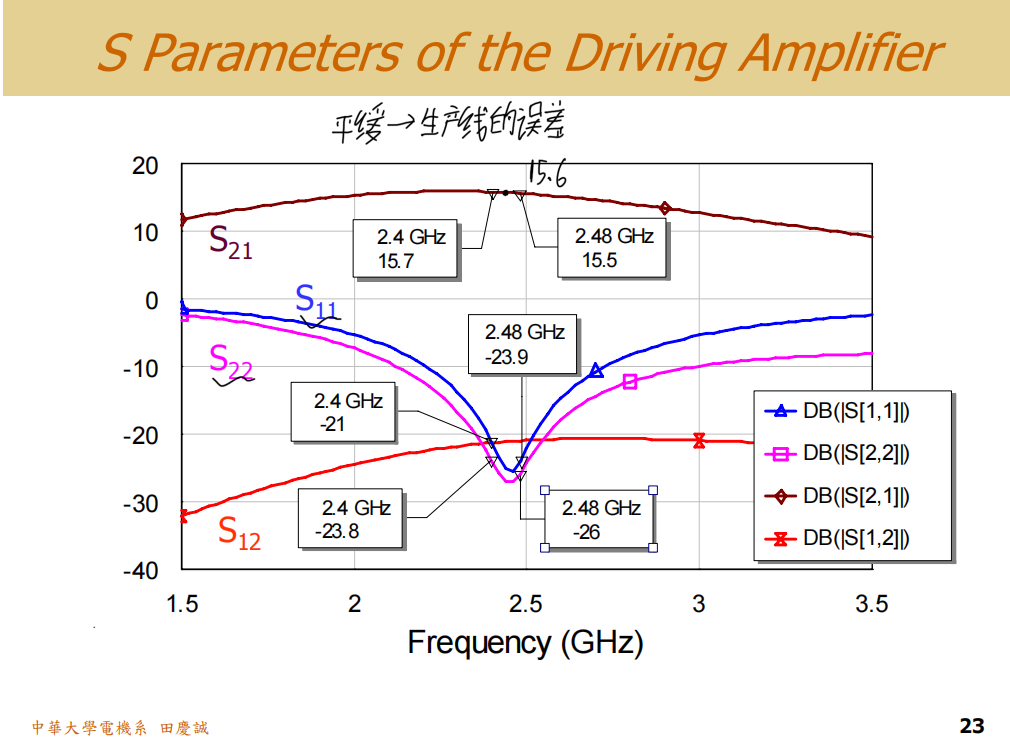
选择 3nH 而非 6nH 的电感，正是为了优化这个特性。如果使用6nH，增益曲线会在低频端出现一个明显的突起，导致响应不平坦。一个平坦且对称的增益响应 不仅是"好看"，更具有重要的工程意义：它意味着放大器对元件的制造公差和生产误差更不敏感。如果工作点在一个陡峭的斜坡上，微小的参数变动就会导致性能急剧变化，这在量产中是灾难性的。

现在，我们注意到这个增益值大约是 15.6dB ，符合我们最初设计的目标。这里有一个非常关键的概念需要澄清：软件在进行这种分析时，会在设定的直流偏压点附近，施加一个极其微小 的交流信号（理论上趋于无穷小）。这样，晶体管始终工作在线性区，其小信号模型完全有效。

因此，这个15.6dB的增益是在输入功率极小的条件下得到的理论最大值。

谐波仿真图

当我们需要评估放大器处理实际信号（具有一定功率）的能力时，就必须进行非线性大信号分析 。在ADS中，我们使用谐波平衡（Harmonic Balance） 仿真器。

第一步：设置与仿真

将输入端口替换为功率源（P1ToneP_{1Tone}P1Tone），并设定扫描的输入功率范围（例如从-30dBm到0dBm）。
在谐波平衡仿真控件中，需要正确设置谐波数量（Number of Harmonics）。对于非线性较强的分析，通常需要设置5个或更多谐波，以确保计算精度。
关键是要测量大信号增益（Large-Signal Gain） 。这不再是简单的S21，而是需要指定：测量输出端口基波（Fundamental， n=1） 功率与输入端口基波（n=1） 功率之比。

第二步：解读结果图

我们得到了一张以输入功率（Input Power） 为横轴、增益（Gain） 和输出功率（Output Power） 为纵轴的曲线图。

增益曲线（蓝色） ：当输入功率极低(-30dBm)时，增益正是我们之前看到的15.6dB（小信号增益）。随着输入功率增大，增益开始逐渐下降 ，这就是增益压缩（Gain Compression） 效应。
1dB压缩点（P1dBP_{1dB}P1dB）的确定 ：
1. 在增益曲线上找到比小信号增益低 1dB 的点（即15.6dB - 1dB = 14.6dB）。图中虚线标出了这一点。
2. 从该点垂直向下，与横轴相交，得到此时的输入功率 （Input P1dBP_{1dB}P1dB,从图中可以读出来为-3.04dBm）。
3. 从该点垂直向上，与基波输出功率曲线（蓝色） 相交，得到此时的基波输出功率 （Output P1dBP_{1dB}P1dB）。图中显示，当增益压缩1dB时，输出功率约为 11.5dBm。
4. 并且从图中可以看到
  基波：在2.445GHz，输出为11.5dBm。
  二次谐波 ：在4.89GHz，输出约为-0.7dBm。
  谐波抑制 ：两者相差约 12dBc 。
  这远未达到我们设计指标中 -20dBc 的要求。根本原因 在于我们偷懒使用了高通型输出匹配网络 ，它对谐波毫无抑制力。要解决这个问题，必须将输出匹配改为低通或带通结构。

结论：

通过谐波平衡仿真，我们得到了放大器的核心功率指标：1dB压缩点输出功率（P1dBP_{1dB}P1dB）约为 11.5dBm 。这超过了我们最初设定的 10dBm 的设计目标，表明从输出功率能力上看，设计是成功的，但抑制谐波上，做得还不够好。

双音测试

好的，我们继续分析谐波平衡仿真结果，并讨论双音测试中的关键概念，以评估放大器的互调失真（IMD）。这是一个极易出错的环节。

双音测试概念

核心概念：双音测试时，输入的是两个频率相近（F1, F2）、幅度相等的信号。
常见错误 ：在进行仿真或阅读数据手册时，必须明确横坐标 Input Power 指的是每个单音的功率（Per-Tone Power） ，还是两个音的总功率（Total Power） 。绝大多数情况下，指的是 Per-Tone Power。
功率换算 ：两个单音信号的总功率比单个音高 3dB 。即：
总功率 (dBm) = 单音功率 (dBm) + 3dB

让我们结合之前的单音（One-Tone）P1dBP_{1dB}P1dB结果来理解：

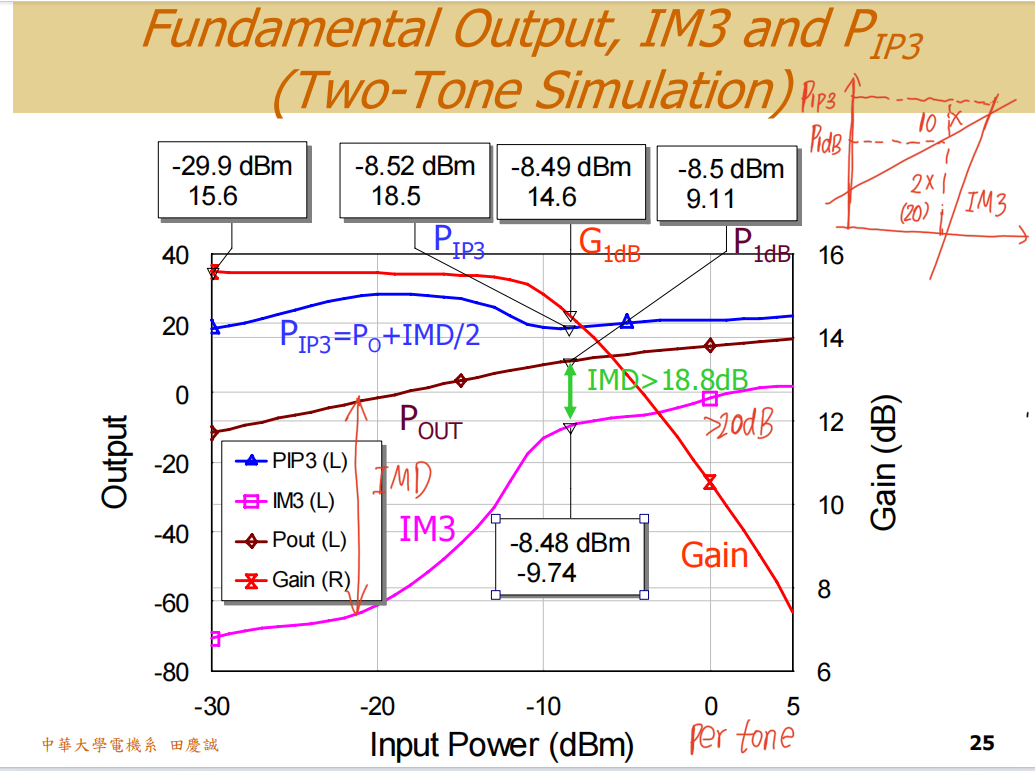
单音测试结果 ：放大器在输入为 -3dBm （单音）时，输出达到P1dBP_{1dB}P1dB（11.5dBm），此时增益压缩1dB。
如果双音测试中，每个音仍输入-3dBm，那么总输入功率将是 0dBm。这已经超过了放大器线性工作的范围（总输入-3dBm时已压缩），会导致严重的互调失真，仿真结果毫无意义。
正确的设定 ：为了保证放大器在双音测试中仍处于合理的线性工作区（接近但不严重压缩），通常需要降低每个单音的输入功率 。例如，将每个单音设为 -6dBm ，这样总输入功率为 -3dBm，与单音测试中达到P1dB的输入总功率一致。

总结：

单音P1dBP_{1dB}P1dB ：通常较高，是数据手册的标称值。在我们的设计中为 11.5dBm。
双音P1dBP_{1dB}P1dB ：由于两个信号相互作用，非线性效应更显著，其有效的1dB压缩点输出功率会比单音测试结果更低 。我们的仿真显示，双音下输出约为 9.05dBm。
工程意义 ：在实际通信系统中，信号是复杂的多载波（类似多音）。因此，用单音P1dB来估算系统线性动态范围时往往过于乐观。在设计链路预算时，需要预留更多回退（Back-off），或参考双音、三阶交调截点（IP3）等指标。

双音测试中的功率定义辨析

在进行双音测试仿真时，一个常见的困惑是关于功率的定义。

常见错误 ：仿真时，测量输出的"Per-Tone Power"（单个音的功率）。例如，在P1dBP_{1dB}P1dB压缩点附近，你可能测到单个音的输出功率是 6.11dBm。
正确解读 ：放大器的总输出功率 是两个音功率之和。因此，实际的总输出P1dBP_{1dB}P1dB应为6.11dBm + 3dB ≈ 9.11dBm。
对比单音P1dBP_{1dB}P1dB ：我们之前单音测试的P1dBP_{1dB}P1dB是 11.5dBm 。双音测试下，有效P1dBP_{1dB}P1dB降到了约 9.11dBm ，下降了约 2.4dB。这是合理的，因为双音信号对放大器的线性度要求更高。
关键结论 ：在阅读数据手册或汇报结果时，必须明确指出P1dBP_{1dB}P1dB、OIP3等指标是基于单音（One-Tone）还是双音（Two-Tone）测试，以及功率是单音功率还是总功率。混淆这些概念会导致严重的性能误判。

三阶交调截点（OIP3）的计算与非线性度评估

我们通过双音测试来计算OIP3。

公式回顾 ：OIP3 (dBm) = PoutP_{out}Pout (dBm) + ΔP/2，其中 PoutP_{out}Pout 是基波总输出功率，ΔP 是基波与三阶互调（IM3）分量的功率差（单位dB）。
非线性度的直观判断 ：一个经典的经验法则是，对于A类放大器 ，在1dB压缩点（P1dBP_{1dB}P1dB）处，其输出功率与IM3功率的差值通常在 20dBc 左右。如果这个差值显著小于20dB，说明线性度较差；如果大于20dB，则线性度更好。
我们的设计 ：在仿真中，我们的A类放大器在P1dBP_{1dB}P1dB点附近，这个差值接近20dB(大于18.8dB)，表明线性度设计基本符合A类放大器的典型特征，但由于小于20dB,说明我们设计的放大器线性度比较差。

负载牵引（Load Pull）等值线图

仿真软件可以算出很高的输出功率（如11.5dBm），但这并不意味着晶体管在实际中能安全地输出这个功率 。

我们需要进行负载线分析（Load Line Analysis） ，检查在最大输出时，晶体管的瞬时工作点是否超出了其最大额定值 （如Vcemax=4.5V,Icmax=35mAVce_{max} = 4.5V, Ic_{max} = 35mAVcemax=4.5V,Icmax=35mA）。

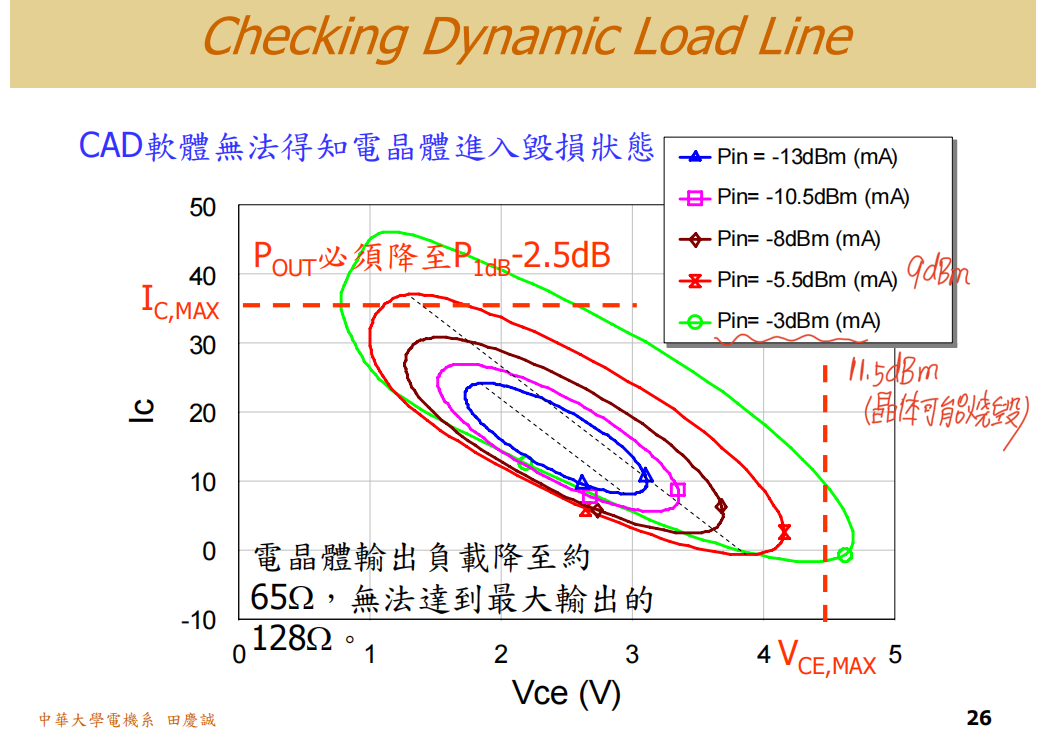
当我们输入-3dBm（单音）以达到仿真的P1dB（11.5dBm）时，晶体管的瞬时电压和电流可能会扫过非常大的范围。
检查负载线 ：通过绘制该输入功率下的负载线（即晶体管集电极电压和电流的瞬时轨迹），我们发现这条线(图中绿色的线)触及甚至超出了 由Vce_max和Ic_max定义的"安全矩形"边界。
- 后果：在实际电路中，这意味着晶体管会进入饱和区或击穿区，产生严重失真、效率骤降，并因过热而迅速烧毁。你会在实验室闻到"煎蛋的味道"。
确定"安全"工作点 ：我们需要降低输入功率，直到负载线完全落在安全区域内。例如，将输入功率降低2.5dB至 -5.5dBm (图中红色线)，此时对应的安全输出功率可能只有约9dBm 。
- 对设计的影响 ：我们最初的设计目标是10dBm输出。如果考虑晶体管的安全工作区，仿真中"看似合格"的11.5dBm实际并不可靠，9dBm的安全输出可能无法满足要求 。这就迫使我们必须：
  - 重新选择晶体管：选用功率余量更大的器件。
  - 调整偏置或匹配：在功率、线性度和效率之间重新权衡。

核心教训：

负载线分析是连接仿真与现实的桥梁。它揭示了理论性能与实际器件极限之间的差距。
一个负责任的射频放大器设计，绝不能止步于S参数和谐波平衡仿真。必须进行负载线分析，确保晶体管在任何瞬时状态下都工作在其绝对最大额定值之内。
否则，设计将只存在于电脑中，无法成为可靠的产品。

为什么输出功率不足？

出现问题，接下来就是分析并解决问题，为什么我们的输出功率会不足呢?

我们最初的理论计算表明，在理想条件下（负载为128Ω纯电阻），晶体管最大可输出约12.15dBm的功率。然而，实际仿真和负载线分析显示，我们的设计只能安全地输出约9dBm的功率。差距主要来自两方面：

实际负载阻抗偏离最佳值：
- 目标负载 ：为获得最大输出功率，晶体管应看到约 128Ω 的纯电阻负载。
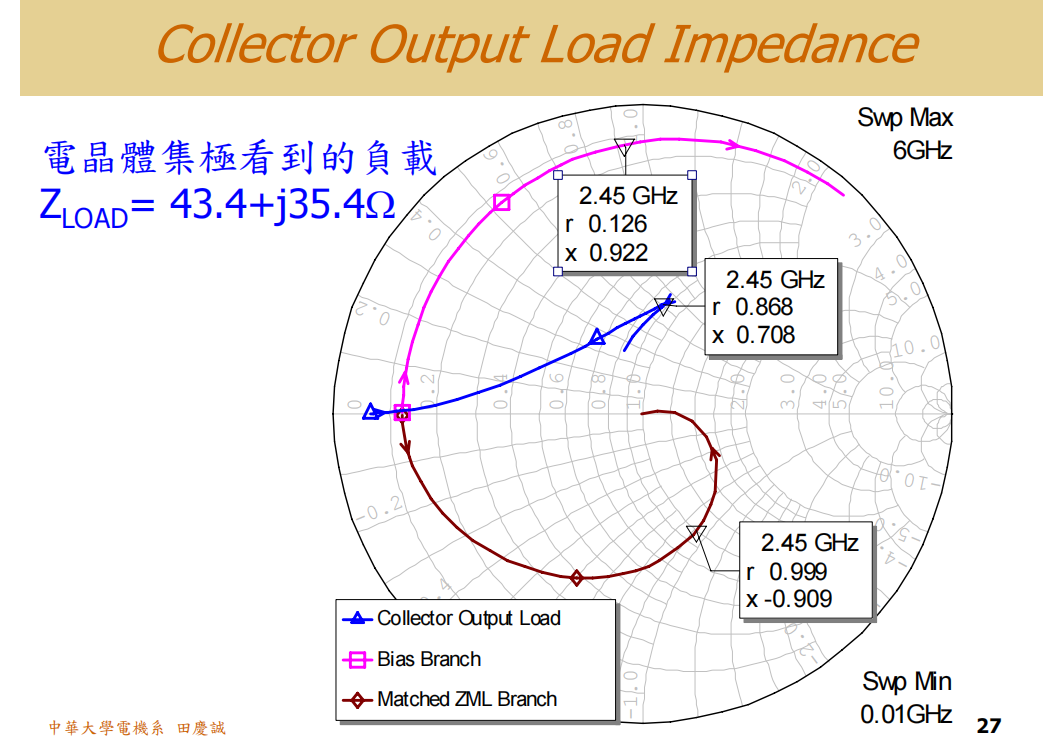
- 实际负载 ：晶体管向外看，看到的不仅是匹配网络和50Ω负载，还包括了偏置/稳定网络 （那个3nH电感和6.25Ω电阻的并联组合）。这个并联路径在2.4GHz的阻抗很低，严重拉低了晶体管看到的总负载阻抗。我们估算的实际等效负载斜率对应的电阻远低于128Ω，大约在65Ω左右，且含有电抗成分。
- 后果：负载阻抗降低，导致负载线斜率变陡。这使得在相同的电压摆幅下，电流摆幅会更大，更容易触碰到最大电流限制；或者为了不超限，不得不限制电压摆幅，两者都导致输出功率下降。
负载的非纯阻性（复数性）：
- 实际负载是复数（包含电抗），这导致集电极电压Vce和电流Ic的瞬时波形存在相位差。
- 后果：在负载线图上，工作点的轨迹从一个理想的斜直线 变成一个椭圆形 。这个椭圆更容易触及由Vce_max和Ic_max划定的"安全矩形"的边界（特别是四个角），进一步限制了安全输出的电压和电流摆幅。

如何提升输出功率？

经过上一节分析，我们知道，输出功率不足的根本原因，主要由于偏置/稳定网络在2.4GHz阻抗过低，拉低了总负载阻抗，且负载为复数导致了低效的椭圆形负载线。

我们的目标是保证稳定性的前提下，提升输出功率。

核心思路是：提高晶体管输出端看到的等效负载阻抗。

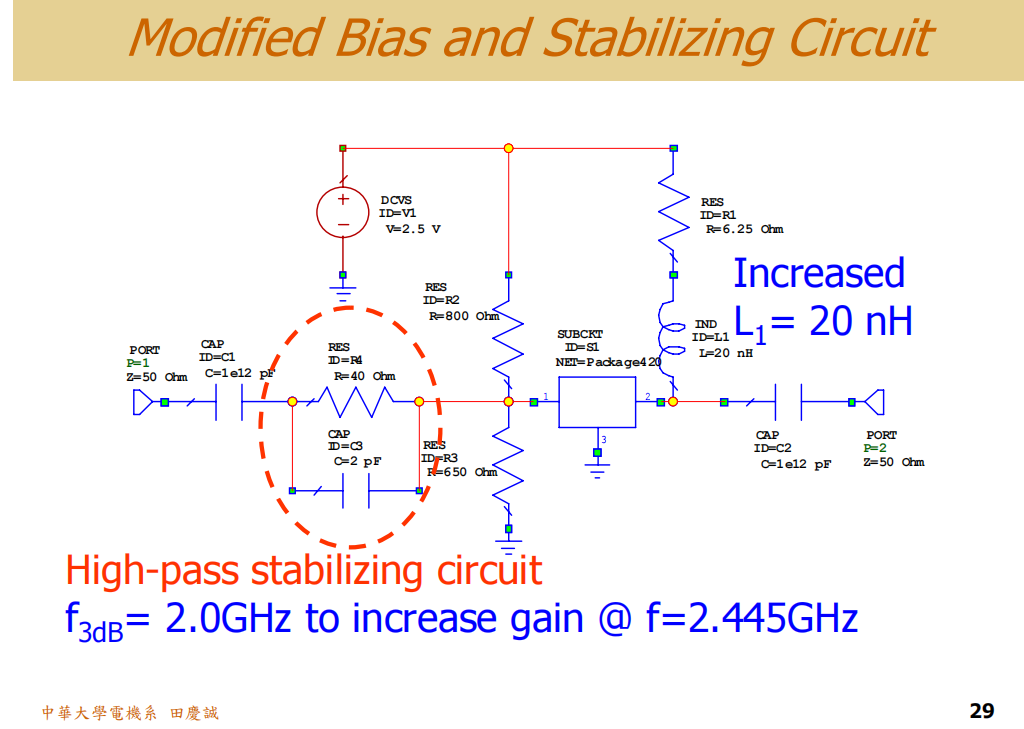
我们目前使用的 3nH 电感值很小，旨在让工作频段（2.4GHz）的信号也能部分"看到"偏置电阻，以压平增益。但这也带来了副作用：在2.4GHz，这个并联支路的阻抗很低，严重分流。

优化方向 ：增大这个电感的值，例如增加到 20nH。这样在2.4GHz，该支路的阻抗会显著提高，对主射频通路的分流作用减弱，从而提升晶体管看到的总负载阻抗。
引发的新问题 ：电感增大后，在较低频段（如几百MHz到2GHz） ，该支路阻抗会降低，可能导致电路在这些频段稳定性变差（K < 1），引发低频振荡。

为了应对电感增大带来的低频稳定性问题，我们可以在输入端额外增加一个针对特定低频的稳定网络。例如，一个串联的RC网络（电阻R和电容C串联后并联到地）：

工作原理 ：该RC网络在某个特定频率（如 f = 1/(2πRC)）呈现较低的阻抗。我们可以将这个频率设定在需要额外稳定性的频段（例如1-2GHz）。在该频段，射频信号会被这个电阻吸收掉，提升K值，确保稳定。而在2.4GHz的工作频段，该RC网络因电容阻抗很低，几乎被短路，对主电路性能影响极小。

这是一种"分频段治理"的策略。用大电感（20nH）保证工作频段的高阻抗，避免功率分流；用专用的RC稳定网络来精准抑制低频不稳定性。

好，我们来看一下结果。

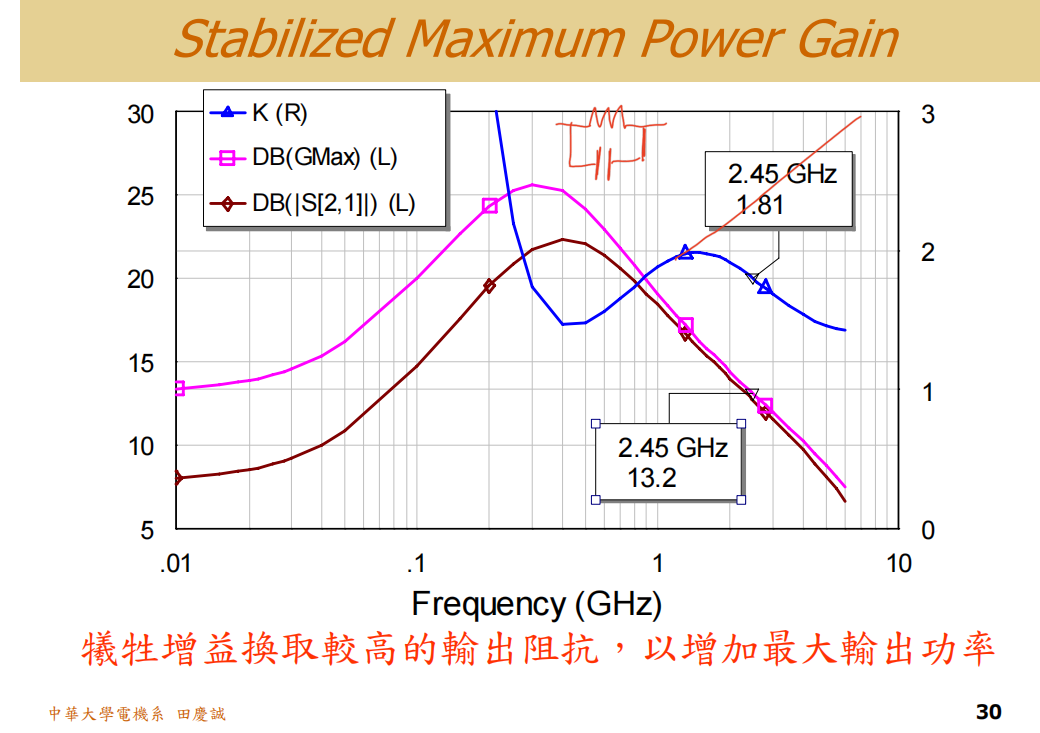
根据之前的仿真结果，如果电感值设定为20nH，我们预计这条K值曲线可能会落在图中这个位置。虽然目标区域（2.4GHz附近）本身是稳定的，但在其他频段可能出现不稳定情况，因此我在电路中加入了一个电阻和一个电容。
加入RC网络的主要作用是在低频段将K值提升上来，使得整体的稳定性得到改善 。从图中可以看到，原本在低频区域K值较低，尤其是在2GHz附近尤为明显。因此，我将RC网络的极点（3dB点）设置在2GHz附近，目的就是让该频点附近的信号一部分被电阻吸收，另一部分通过，从而在2GHz附近适度降低增益，避免K值过低。

通过这样的调整，我们再看仿真结果：你会发现K值曲线出现了一个上翘的趋势 ，这正是因为我们在2GHz附近引入了损耗控制。而在频率较高时，由于电容通路阻抗降低，信号更多地从电容通过，从而使K值有所下降------如果没有电容，只加电阻的话，K值原本会更高一些。这样通过电容将高频段的K值拉低，就能避免增益下降过多。

这样的设计方法需要根据实际需求灵活调整，并且关键是要学会解读仿真曲线 。每次仿真后，都应该养成分析曲线变化的习惯，理解每个元件或结构调整会带来怎样的性能变化。这样在实际进行电路调优或架构修改时，你才能迅速判断该怎么做，而不是盲目尝试。

接下来再看，在这个结果中，我们可以看到在2.45GHz处，GmaxG_{max}Gmax和S21S_{21}S21两条曲线几乎完全重合。这其实意味着匹配网络几乎可以简化甚至省略 。

当然，不要忘了我们最初目的，其实是通过牺牲一定的增益，来换取更高的输出阻抗。从仿真中可以看到，输出阻抗从原来的约40+j30Ω，提升到了接近60+j21Ω，电阻部分提升了约30%，电抗部分下降了约40%。

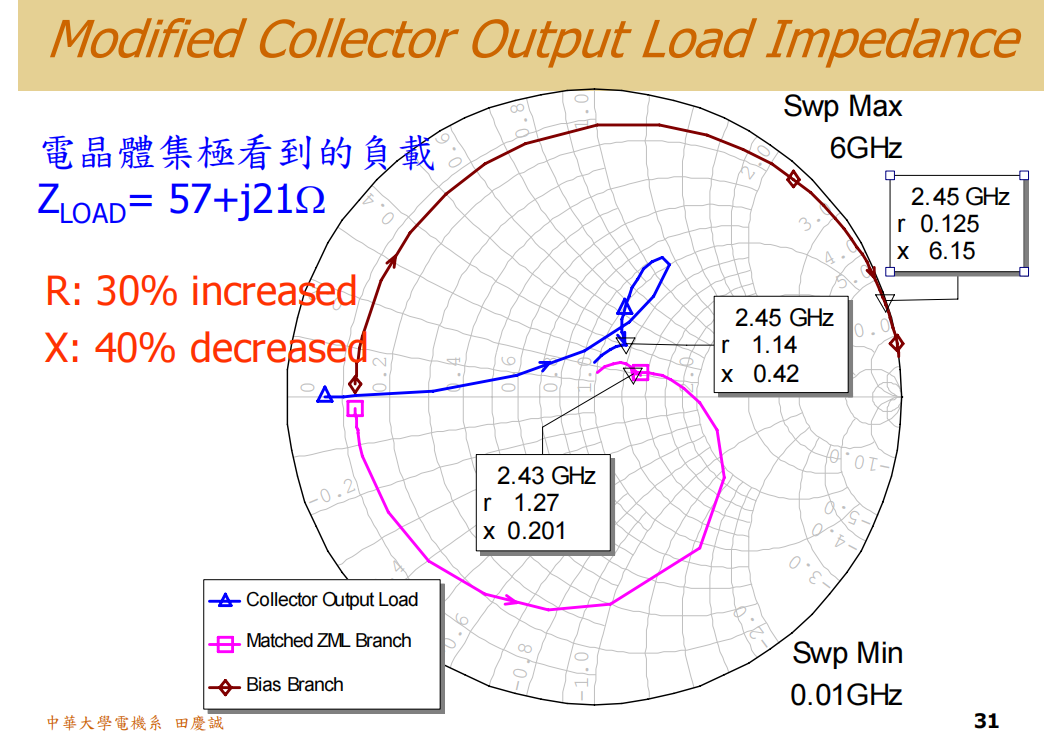
输出阻抗更靠近中心点后，我们再次进行匹配计算。在给定条件下求得最佳解时发现，此时的两个解比之前更接近50Ω。这也印证了刚才曲线的趋势：当GmaxG_{max}Gmax和S21S_{21}S21非常接近时，说明只需简单的匹配即可实现较好的性能。

重构匹配网络

根据新的晶体管阻抗（因偏置网络改变而提升），我们重新设计了低通型（Low-Pass）的输入和输出匹配网络 ，以抑制谐波。

好，接着我们来看输入端的电路设计。我在这里采用了高通匹配结构 ，总共用了三个元件。其实原本从起点到终点，只用串联一个电感加并联一个电容就可以实现匹配，但我们故意调整了匹配路径，让它绕得更远一些。

这样做的目的是什么呢？主要是为了更好地抑制低频增益。如果直接匹配过去，低频段的增益压不下来。通过把路径拉开，频率响应会变得更窄，也就是Q值更高，这样对低频的抑制效果会更明显。因为在这个设计中，低频增益原本就偏高，需要更有效地压低。

再看输出端。之前只有一个电容，但在实际谐波抑制要求下 ，我们需要一个低通匹配网络来控制谐波。这里同样采用两个元件构成低通结构。原本直接用一个并联电感和一个串联电容就能完成匹配，但这样高频抑制效果不够理想。因此我选择让匹配路径先"绕远一点"再拉回来，目的是让频率响应在高端滚降更快，对高频谐波的抑制更强。

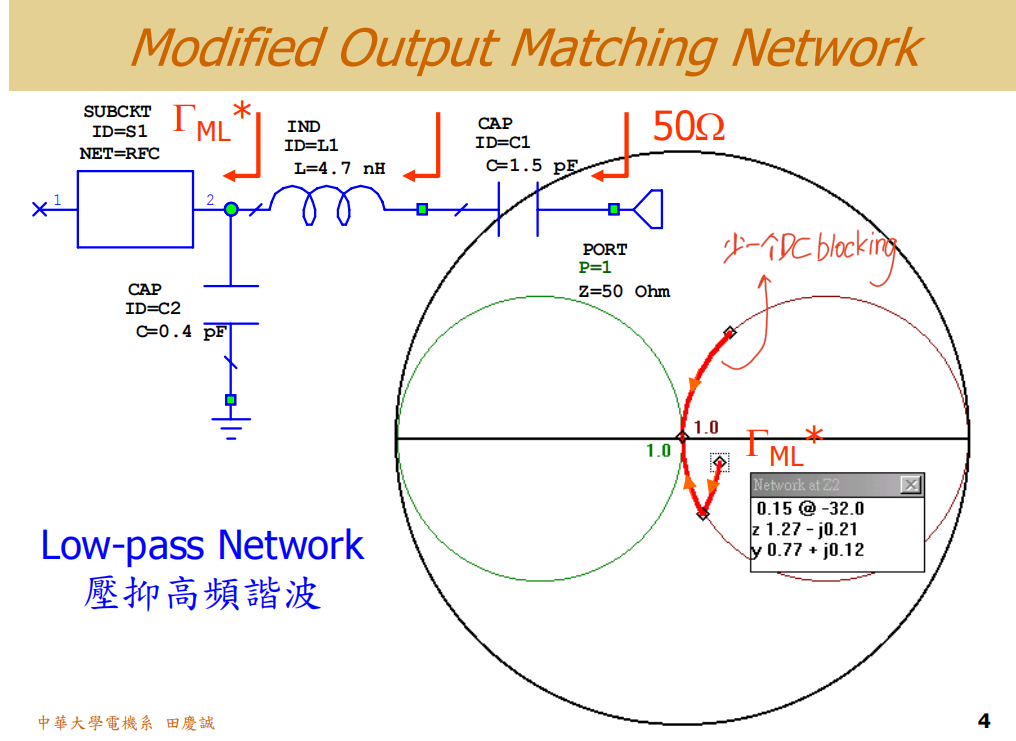
这样的绕路设计还有一个额外的好处：如果直接从起点并联电容再串联电感，直流通路会受到影响，可能需要额外加隔直电容。而现在这样走线，多串联的这个电容本身就可以起到隔直作用 ，既简化了结构，又让频率响应更符合需求。

所以，在设计匹配电路时，不必墨守成规地追求最短路径。适当调整拓扑走向，既能优化频率响应，又能兼顾其他功能需求，让整体性能更加完善。

完整设计电路如下:

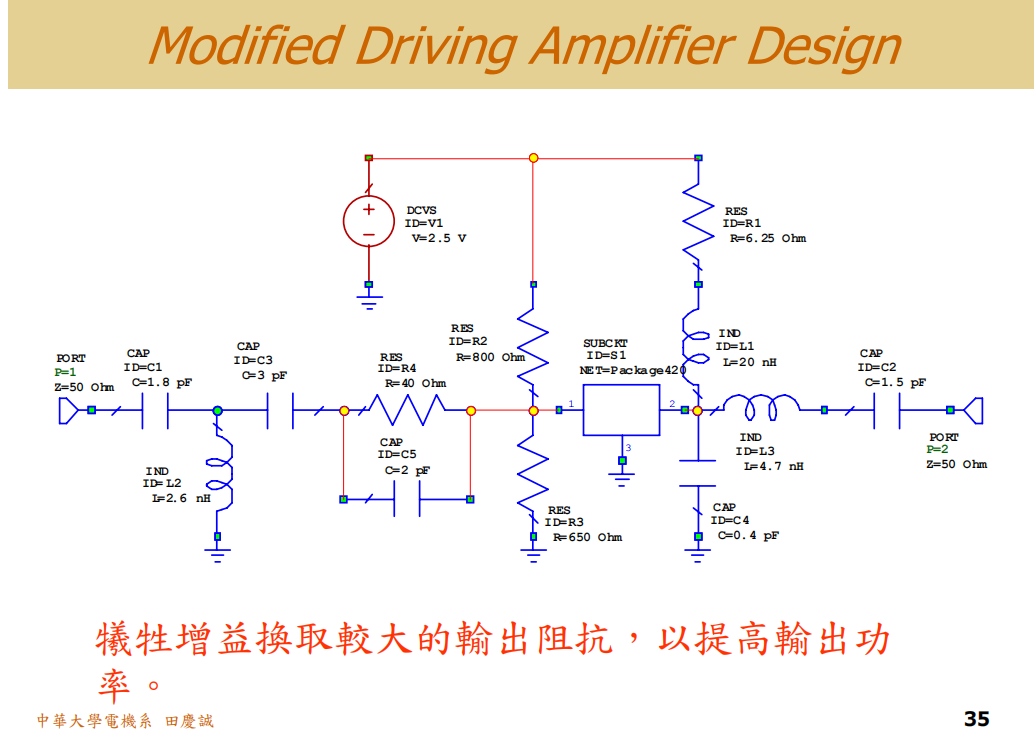
重新验证

好，接下来整个电路已经设计完成，我们开始来看模拟结果。

1. S参数

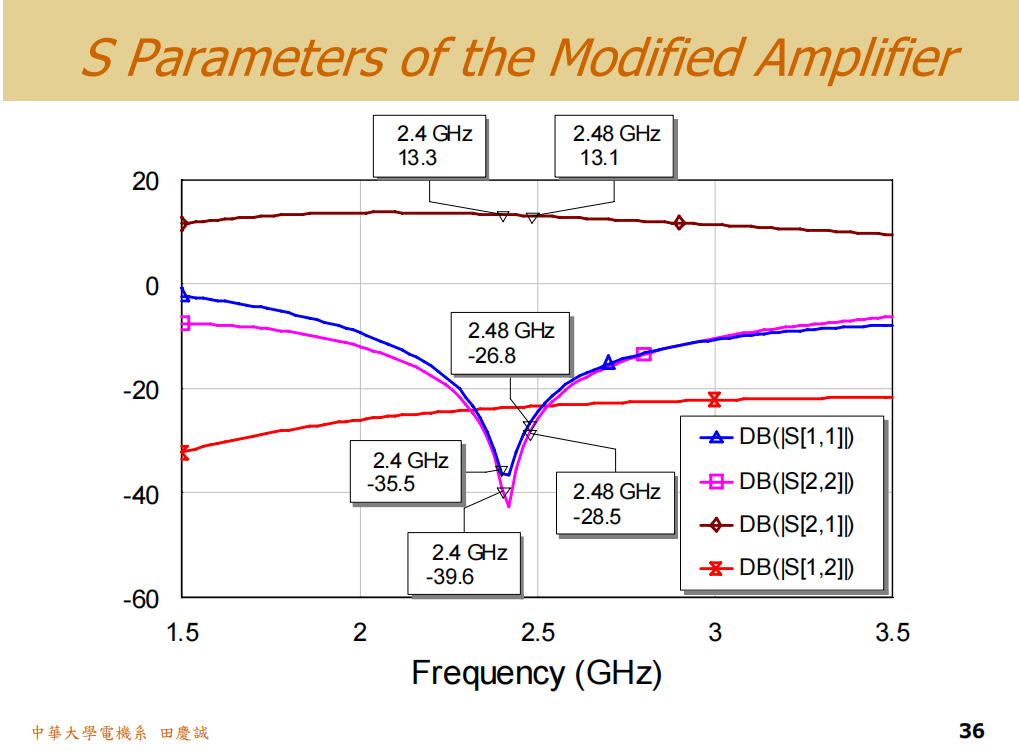
首先看小信号的S参数。增益大约是13.2dB，这在我预期的范围之内。同时，S11和S22的匹配效果都做得非常好，和预期的设计目标一致。

这里我再次建议大家，输入和输出的匹配尽量都要做好 。有些人可能会想："我刚好把增益做到2.0dB就可以了，输出匹配稍微牺牲一点没关系。"但实际上，当你把电路与其他部分级联时，输出匹配不好会导致整个系统性能恶化，可能会出现各种难以预料的问题。
所以，最好将S11和S22都做到足够好，这样可以减少很多后续组装和调试的麻烦。

2. 谐波仿真

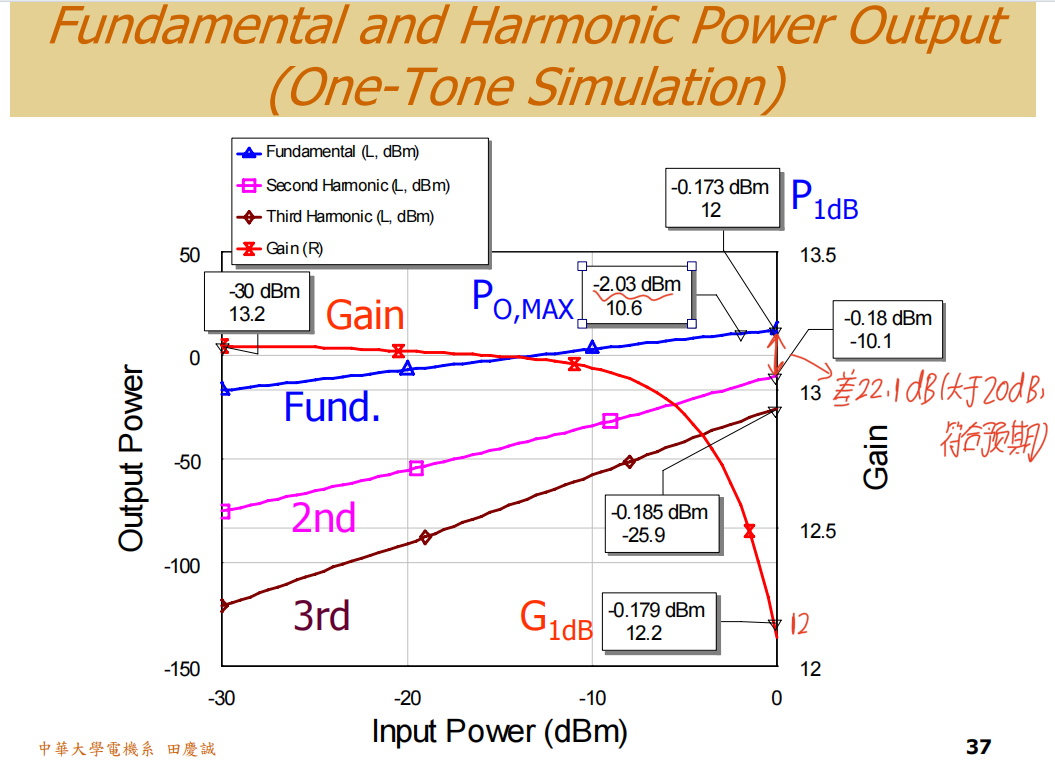
接下来我们看功率特性。先看增益，它从13.2dB下降到了12.2dB（图中红色曲线表示增益压缩）。然后我们往上画一条线，和蓝色线相交，可以读出输出功率为12dBm.也就是说，由于我们提升了输出阻抗,我们在P1dBP_{1dB}P1dB点的功率输出可以达到约12dBm，比之前有所提高。

更重要的是，在P1dBP_{1dB}P1dB点（12dBm输出）时，我的二次谐波（HD2）大约在-10dBc。这样一来，基波与二次谐波的差值达到了22dB，比之前的12dB改善了整整10dB。**这正是因为我们加入了低通匹配网络，将谐波压制了大约20dB。**这个结果是可以接受的，通常至少需要20dB的抑制。因为有低通结构，高次谐波也会被一并压制下去。

3. 动态负载线

我们接着来看下一组结果，关于动态负载线 的分析。

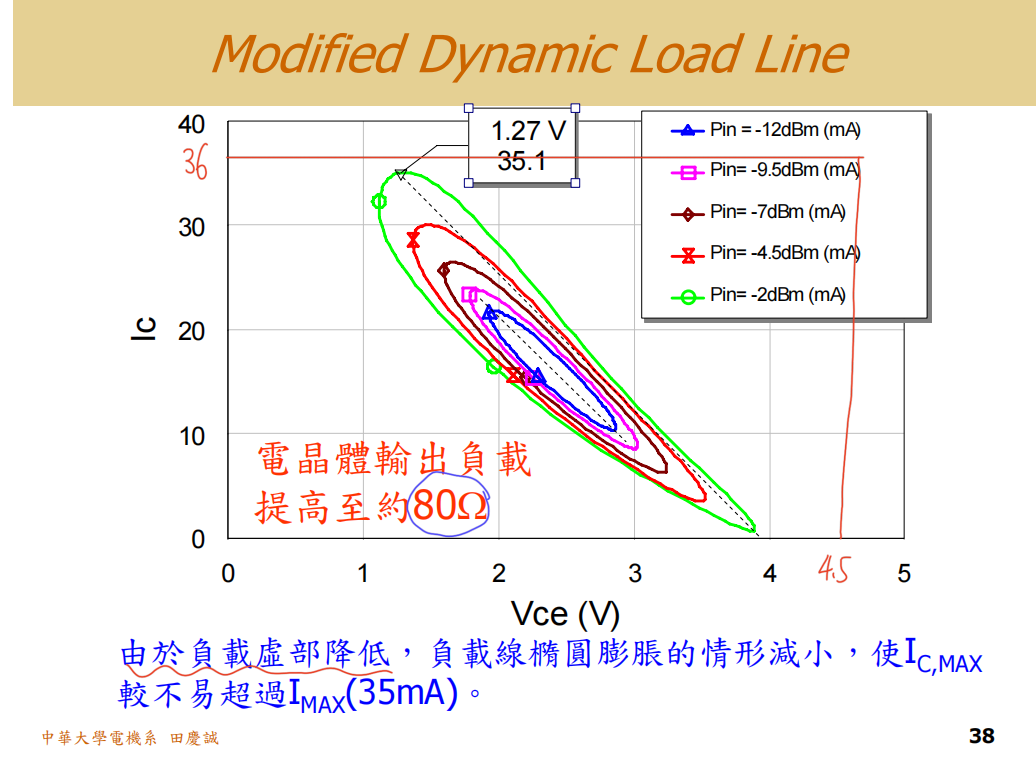
我们需要检验一下，在实际的"单音"（One-Tone）仿真中，这个P1dB（12dBm）是否真的可用。我检查了此时的输入功率（Pin），发现是0dBm。但看电流波形，在Pin=0dBm时，电流峰值已经达到了约36mA，接近或超过了晶体管的安全工作区（图中显示限制在35mA左右）。这说明虽然P1dB标称是12dBm，但在Pin=0dBm时，器件可能已经工作在临界饱和或过载状态。

因此，我们找到一个更安全的回退（Back-off）工作点 。当Pin = -2dBm时（图中绿色曲线），电流峰值刚好落在安全区域的边界。所以，实际可安全使用的P1dB对应的Pin大约是-2dBm。

在Pin = -2dBm时，对应的输出功率Pout大约是10.6dBm。所以，我们安全的P1dB从之前的9dBm提升到了10.6dBm ，提高了1.6dBm。这已经满足了设计要求的10dBm，并且有了0.6dB的余量。由于我们需要兼顾前后级匹配，输出负载不可能无限优化，所以这个提升幅度是合理且有效的。
这个改善的关键在于负载的虚部（电抗部分）降低了 。从仿真结果看，实部负载提升到了接近60欧姆，而虚部负载降低到了21欧姆左右。虚部变小后，负载椭圆在史密斯圆图上变得更"瘦长"，使得电流的动态范围缩小，更不容易超出35mA的额定限制。

因此，调整负载的虚部，让其变小，对于改善线性工作区和安全范围的效果非常明显。(胖椭圆变瘦椭圆)

4.双音仿真

最后，我们看一下双音（Two-Tone）仿真的结果。

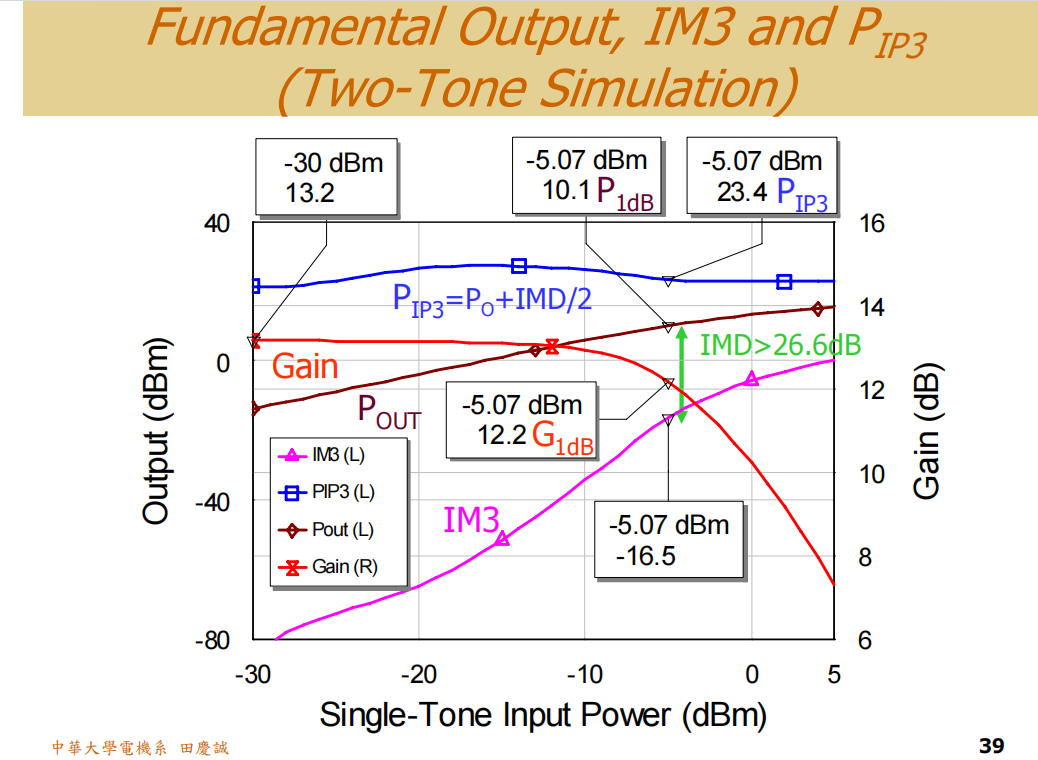
在增益从13.2dB压缩到12.2dB（即P1dB点）时，对应的输出功率是10.1dBm（与理论值12dBm有差距，实际仿真总会略差一些）。

再看IP3（三阶交调截点） ，上一次设计大约是18dBm，现在提升到了约23.4dBm，改善了接近5dB。

这个IP3的提升，与后级谐波负载的处理密切相关。因为互调失真（IMD）会受到后级谐波端所呈现的负载影响。从结果可以看到，三阶互调分量（IMD3）的抑制比之前改善了约7-8dB。由于IP3的改善量大约是IMD3改善量的一半，所以这里IP3提升了约4dB是合理的。
互调抑制改善 ：在P1dB点，三阶互调（IM3）抑制从约18dBc改善至 26.6dBc 。这说明输出匹配网络的低通特性不仅抑制了谐波，也显著改善了互调失真性能 。

总而言之，通过这次设计，我们优化了匹配网络，在保证增益和匹配良好的前提下，有效提升了输出功率能力、谐波抑制和线性度。关键在于理解并灵活运用匹配拓扑，同时密切关注负载线、电流摆幅和失真指标之间的权衡关系。

让我们对优化后的设计进行最终的性能检验和总结。

最终规格

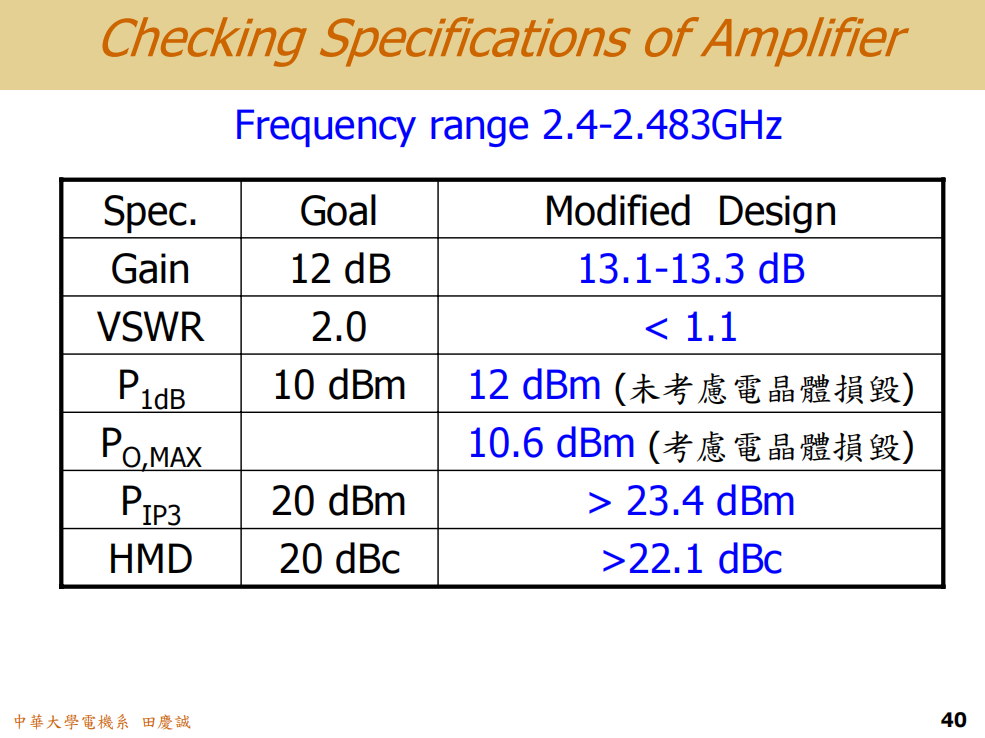
增益：13.2dB (目标：≥10dB)
输入/输出匹配：VSWR ≈ 1.1 (目标：≤ 2.0)
输出功率（安全P1dB）：10.6dBm (目标：≥10dBm)
谐波抑制（二次）：22dBc (目标：≥20dBc)
线性度（OIP3）：23.4dBm

经过这一轮的优化调整，我们的电路增益从最初的大约16-17dB下降到了13dB。对于要求一级增益12dB的目标来说，这个结果是完全可以接受的。在匹配方面，我们的电压驻波比（VSWR）表现非常好，输入和输出端都达到了约1.1，几乎是完全匹配的状态。

这里要特别强调匹配的重要性。如果你的电路VSWR做得好（比如1.1），即使你连接的后级电路（例如混频器）的VSWR很差（比如高达4），整个级联系统通常也不会出大问题。

为什么呢？还记得信号流图（Signal Flow Graph）的分析吗？系统总的反射系数与你自身以及后级的反射系数都有关。如果你的反射系数很低，即使对方的反射系数很高，两者的"环路增益"乘积依然会很小，整个系统的稳定性就得到了保障。

反过来，如果你的设计刚刚好卡在VSWR=2.0的边界上，而后级电路VSWR又很差，两者级联后，总的反射效应可能会被放大，导致增益严重恶化、性能不稳定等奇怪的问题，而且调试起来会非常困难。所以，宁可把自己的匹配做到极致，这样在面对各种不理想的后续电路时，你都有足够的余量来保证系统正常工作。

在功率性能方面：

P1dB：如果不考虑负载牵引的极限，仿真显示约为12dBm。如果考虑电流安全区等实际限制，我们找到了一个更安全的回退工作点，实际可用的P1dB约为10.6dBm，比之前提升了约1.6dBm。
IP3：从之前的约18dBm提升到了23.4dBm，改善了约5dB。
谐波抑制：二次谐波抑制（HD2）从12dB提升到了22dB，改善了10dB。

这些改进都与输出匹配网络的优化密切相关。所以，匹配设计绝不简单，它需要综合考虑多个因素：

稳定性：匹配网络可能引入反馈路径，影响稳定性（尤其是多级放大器的级间匹配）。通常匹配做得越"窄"（高Q值），潜在的稳定性风险可能越大。
对谐波的影响 ：采用高通（High-Pass）或低通（Low-Pass）匹配结构，会直接影响输出端谐波所"看到"的负载阻抗。这又会反过来影响放大器的互调失真（IMD）和线性度（IP3）。如何通过优化谐波负载来抑制互调失真，这是一个非常值得研究的课题，无论是在学术界还是产业界都很有价值。

综上，所有关键指标均已满足或超越设计要求。

如果晶体管的SPICE模型不准，仿真结果可能和实测相差甚远。但这并不意味着仿真软件没用了。关键在于转换思路：仿真不是为了给你一个"绝对正确"的答案，而是为你提供一个性能变化的"趋势"指导。例如，你可以通过仿真观察，当某个电容值增大时，中心频率是向低频移动还是高频移动，增益是上升还是下降。利用这个趋势，你就能在实物调试中知道该往哪个方向调整，而不是盲目乱试。

另一种更精确但有限制的方法是：直接使用测量得到的晶体管S参数进行小信号仿真，并结合实际的布局和元件模型。这样做出来的仿真与实测吻合度会非常高，很有成就感。但缺点是，S参数模型是线性的，无法用于预测功率压缩（P1dB）、谐波（One-Tone）或互调失真（Two-Tone）等大信号非线性性能。因此，这种方法适用于输出功率要求不高的LNA设计，但不适合功率放大器（PA）的设计。