一、SVM
支持向量机(Support Vector Machine, SVM)是一种基于统计学习理论 的监督学习算法,核心目标是在特征空间中构造最大间隔超平面
1.核函数
线性不可分情况:在二维空间无法用一条直线分开,映射到三维(或者更高维)空间即可解决。
目标:找到一个Φ(x)(核函数),对原始数据做一个变换。
举例:
假如有两个数据,x1=(x1,×2,×3)x2=(Y1,y2:Y3),如果数据在三维空间无法线性可分,我们通过核函数将其从三维空间映射到更高的九维空间,那么此时:
f(X)=(x1x1,x1x2,x1x3,x2x1,x2x2,x2x3,x3x1,x3x2,x3x3)
如果计算内积的话,x1与x2计算即<f(x1)·f(x2)>,此时计算复杂度为:9*9=81,原始数据复杂度为
3*3=9,那么对于映射到n为空间,复杂度为:O(n^2)
对于数据点:x1=(1,2,3), x2=(4,5,6),则f(x1)=(1,2,3,2,4,6,3,6,9),f(x2)=(16,20,24,20,25,30,24,30,36),
此时计算<f(x1)·f(x2)>=16+240+72+40+100+180+72+180+324=1024
K(x,y)=(<x1,x2>)^2=(4+10+18)^2=32^2=1024
即:K(x,y)=(<x,y>)^2=<f(x1)·f(x2)>[先内积再平方与先映射再内积结果一致]
特性 :在低维空间完成高维空间的运算,结果一致,大大降低了高维空间计算的复杂度。
本质:在找到一个(核)函数,将原始数据变换到高维空间,但是高维数据可以在低维运算。
2.常用核函数
1.多项式核函数
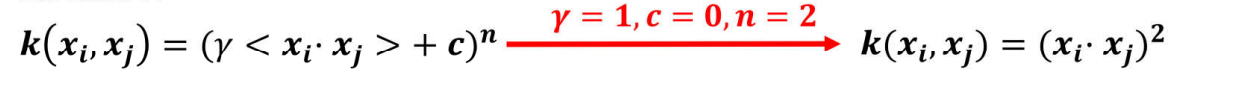
假如有两个数据,x1=(x1,x2),x2=(y1,y2),如果数据在二维空间无法线性可分,我们通过核函数将其从二维空间映射到更高的三维空间,那么此时:

更具体的例子:x1=(1,2),x2=(3,4)
(1)转换到三维再内积(高维运算)

(2)先内积,再平方(低维运算)

2.高斯核函数
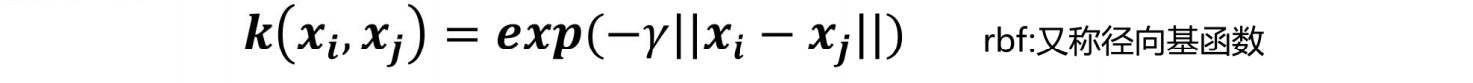
1.当y值越小的时候,正态分布越胖,辐射的数据范围越大,过拟合风险越低。
2.当y值越大的时候,正态分布越瘦,辐射的数据范围越小,过拟合风险越高。
优点:
1.有严格的数学理论支持,可解释性强,不同于传统的统计方法能简化我们遇到的问题。
2.能找出对任务有关键影响的样本,即支持向量。
3.软间隔可以有效松弛目标函数。
4.核函数可以有效解决非线性问题。
5.SVM在小样本训练集上能够得到比其它算法好很多的结果。
缺点:
1.对大规模训练样本难以实施。
SVM的空间消耗主要是存储训练样本和核矩阵,当样本数目很大时该矩阵的存储和计算将
耗费大量的机器内存和运算时间。超过十万及以上不建议使用SVM。
2.对参数和核函数选择敏感。
支持向量机性能的优劣主要取决于核函数的选取,所以对于一个实际问题而言,如何根据
实际的数据模型选择合适的核函数从而构造SVM算法。目前没有好的解决方法解决核函数的选择问题。
3.模型预测时,预测时间与支持向量的个数成正比。当支持向量的数量较大时,预测计算复杂
度较高。
3.支持向量机的API文档
class sklearn.svm.SVC (C=1.0 , kernel='rbf' , degree=3 , gamma='auto_deprecated' , coef0=0.0 , shrinking=True , probability=False , tol=0.001 , cache_size=200 , class_weight=None , verbose=False , max_iter=-1 , decision_function_shape='ovr' , random_state=None )[source]
重要的参数有:C、kernel、degree、gamma。
1.C ****:****惩罚因子【浮点数,默认为1.】【软间隔】
(1)C越大,对误分类的惩罚增大,希望松弛变量接近0,趋向于对训练集全分对的情况,这样对训练集测试时准确率很高,但泛化能力弱;
(2)C值小,对误分类的惩罚减小,允许容错,将他们当成噪声点,泛化能力较强。
->>建议通过交叉验证来选择
2. kernel : 核函数【默认rbf(径向基核函数|高斯核函数)】
可以选择线性(linear)、多项式(poly)、sigmoid
->>多数情况下选择rbf
3 .degree:【整型,默认3维】
4. gamma: 'rbf','poly' 和'sigmoid'的核函数参数。默认是'auto'。
(1)如果gamma是'auto',那么实际系数是1 / n_features,也就是数据如果有10个特征,那么gamma值维0.1。(sklearn0.21版本)
(2)在sklearn0.22版本中,默认为'scale',此时gamma=1 / (n_features*X.var())
#X.var()数据集所有值的方差。
<1>gamma越大,过拟合风险越高
<2> gamma越小,过拟合风险越低
->>建议通过交叉验证来选择