射频网课学习第六章(功率增益圆)

好的，今天我们开始讲解课程的第六部分：功率圆图。

回顾

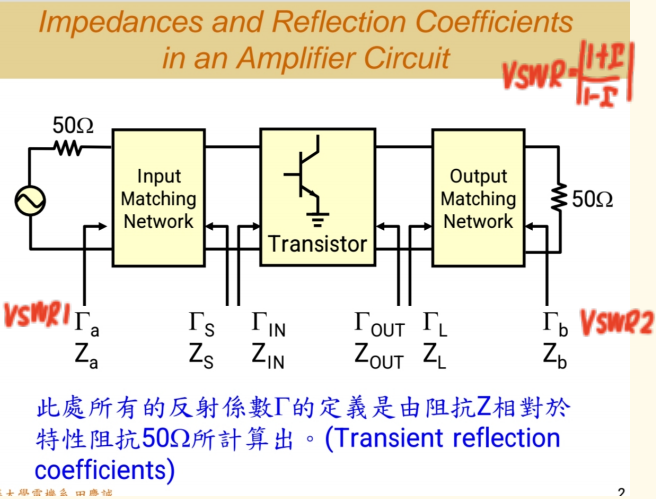
在深入讲解圆图之前，照例我们需要先复习一些基础知识。接下来我们会频繁用到阻抗和反射系数 的相关定义，所以让我们再梳理一遍。

阻抗（例如ZaZ_aZa）与系统参考阻抗（通常是50欧姆）相比较，会形成一个反射系数（Γa\Gamma_aΓa).

这个反射系数在复平面上对应一个点，其计算公式我们之前学过：
Γa=Za−50Za+50\Gamma_a = \frac{Z_a - 50}{Z_a + 50}Γa=Za+50Za−50

这些参数等下都会用到，请大家牢记。

在一个放大器中，从输入端看进去的反射系数是 (Γa\Gamma_aΓa)，它决定了输入端的电压驻波比（VSWR1VSWR_{1}VSWR1）。从输出端看进去的反射系数是 (Γb\Gamma_bΓb)，它决定了输出端的电压驻波比（VSWR2VSWR_2VSWR2）。
反射系数与VSWR的关系是(两者一一对应)：
VSWR=1+∣Γ∣1−∣Γ∣VSWR = \frac{1 + |\Gamma|}{1 - |\Gamma|}VSWR=1−∣Γ∣1+∣Γ∣

接下来，我们复习转换功率增益 (GTG_TGT) 的定义。它的表达式有两种等价的写法，区别在于如何看待系统内部的多次反射效应：

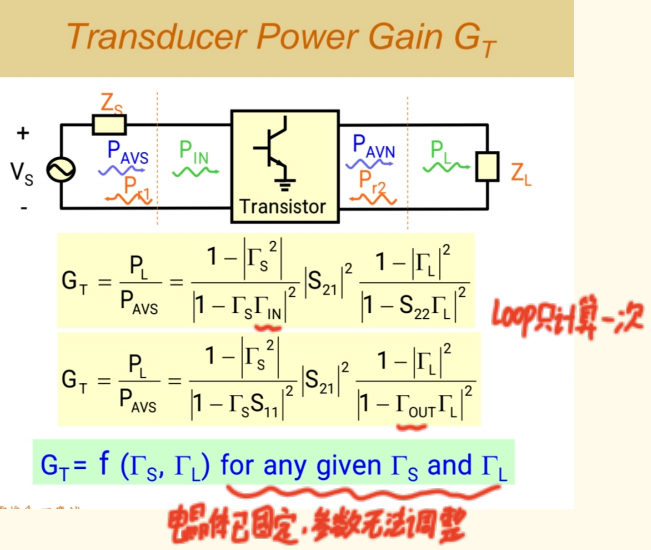
第一种写法 ：从输入端看进去时，使用 Γin\Gamma_{in}Γin 。这个 Γin\Gamma_{in}Γin已经包含了晶体管自身参数S11S_{11}S11以及** 负载反射ΓL\Gamma_LΓL 通过晶体管内部反馈（(S12,S21,S22(S_{12}, S_{21}, S_{22}(S12,S21,S22）引起的所有多次反射的净效应** 。此时，从输出端看过去，我们只考虑晶体管自身的 (S22(S_{22}(S22)。
第二种写法 ：从输入端看进去时，只考虑晶体管自身的S11S_{11}S11。此时，从输出端看过去，我们使用 Γout\Gamma_{out}Γout 。这个Γout\Gamma_{out}Γout 已经包含了晶体管自身参数S22S_{22}S22以及源反射ΓS\Gamma_SΓS 通过晶体管内部反馈引起的所有多次反射的净效应。

这两种方法都是正确的，关键在于不能在同一公式中重复计算 多次反射效应。无论采用哪种写法，转换功率增益GTG_TGT本质上都是一个关于两个变量的函数：源反射系数ΓS\Gamma_SΓS和负载反射系数ΓL\Gamma_LΓL。

功率增益定义总结

那么，在实际设计中，我们如何选择ΓS\Gamma_SΓS和ΓL\Gamma_LΓL呢？这取决于设计目标和晶体管的稳定性：

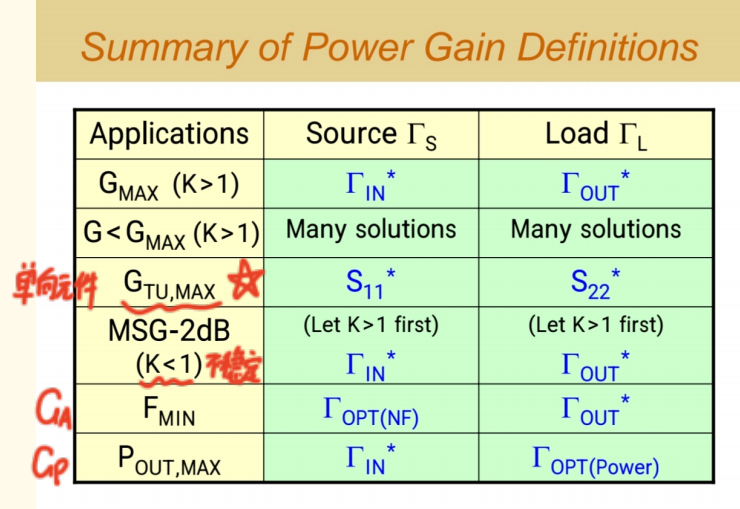
1.追求最大增益 (GmaxG_{max}Gmax)，且晶体管绝对稳定 (K>1) ：

此时存在唯一解 ，即实现双向共轭匹配 ：
ΓS=Γin∗,ΓL=Γout\Gamma_S = \Gamma_{in}^*, \quad \Gamma_L = \Gamma_{out}ΓS=Γin∗,ΓL=Γout

这能让我们得到该晶体管在该频率下的最大可能增益GmaxG_{max}Gmax。
2.晶体管绝对稳定(K>1)，但不需要最大增益 ：

如果我们愿意接受一个低于GmaxG_{max}Gmax的特定增益值 (G)，那么满足该增益条件的ΓS\Gamma_SΓS和ΓL\Gamma_LΓL将有无限多组解 。

这些解在史密斯圆图上会分别构成两个圆，称为等增益圆 。它就是我们本章要学习的主角。

所有落在源端等增益圆上的ΓS\Gamma_SΓS，都能实现相同的增益GGG；负载端同理。
3.采用单向化设计假设 (S12S_{12}S12=0) ：

这是一种简化方法，假设晶体管是单向的（信号只从输入传到输出）。此时，匹配条件简化为：
ΓS=S11∗,ΓL=S22∗\Gamma_S = S_{11}^*, \quad \Gamma_L = S_{22}^*ΓS=S11∗,ΓL=S22∗

许多业界工程师会不假思索地采用这种方法，但我必须指出，这通常是错误的做法 ，除非晶体管真的接近单向S12≈0S_{12} \approx 0S12≈0。

我遇到过毕业多年的学生，他们仍在使用这种方法，结果设计出来的放大器性能总是不理想S11S_{11}S11和 S22S_{22}S22在目标频点并非最佳。原因就在于这种方法忽略了S12S_{12}S12带来的反馈效应，会引入误差。
4.不稳定设计(K<1) ：

前面讨论的三种设计方法（最大增益、等增益圆、单向化设计）都基于一个共同前提：晶体管是绝对稳定的（稳定因子 K > 1） 。在这种情况下，设计有明确的路径，但晶体管也可能并非稳定，即K < 1

此时我们通常将增益设计在比最大稳定增益 MSG 低 2 dB 的位置，当 K < 1 时，理论上增益可以做到无限大（即产生振荡）。选择比 MSG 低 2 dB，是在增益和稳定性之间取得的一个经验性缓冲区。

但强烈不建议 各位在实际工程中直接对不稳定的晶体管进行匹配设计。老板或客户通常不会接受这种高风险方案。无论如何，正规且推荐的做法 是：先使用电阻等无源元件对晶体管进行稳定化处理，使其在整个工作频段内 K > 1 。然后，再按照绝对稳定的条件进行设计，通过双向共轭匹配ΓS=Γin∗\Gamma_S = \Gamma_{in}^*ΓS=Γin∗，ΓL=Γout∗\Gamma_L = \Gamma_{out}^*ΓL=Γout∗来获得最大可用增益 GmaxG_{max}Gmax。

针对不同的设计目标，匹配策略也不同：
5.最低噪声（LNA设计） ：

目标是实现最小噪声系数 FminF_{min}Fmin。
源匹配 ：ΓS\Gamma_SΓS应等于最佳噪声反射系数 Γopt\Gamma_{opt}Γopt。
负载匹配 ：在输出端进行共轭匹配ΓL=Γout∗\Gamma_L = \Gamma_{out}^*ΓL=Γout∗，以提取最大功率。

此时获得的增益称为可用功率增益GAG_AGA。这是一种"输入失配（为噪声优化），输出匹配 "的策略。
6.最大功率（PA设计） ：

目标是向负载输送最大功率。
源匹配 ：在输入端进行共轭匹配ΓS=Γin∗\Gamma_S = \Gamma_{in}^*ΓS=Γin∗，以获得最大功率传输。
负载匹配 ：ΓL\Gamma_LΓL应等于由晶体管直流I-V曲线确定的最佳负载阻抗ZoptZ_{opt}Zopt（而非S22∗S_{22}^*S22∗）。ZoptZ_{opt}Zopt由最大电压摆幅和最大电流摆幅共同决定，其倒数就是负载线的斜率。这是一种"输入匹配，输出失配（为功率优化） "的策略，此时增益为功率增益GPG_PGP。

两种核心设计范式与对应的圆图

接下来，我们将介绍两种设计范式和它们所依赖的两种圆图：等增益圆 和 等驻波比圆（等反射系数圆）。

单向化设计（Unilateral Case）：
- 假设：晶体管为单向元件，即 S12=0S_{12} = 0S12=0。(准确度很低,除非晶体管真的接近单向）
- 设计内容 ：我们会讨论最大单向化增益 UTU,maxU_{TU,max}UTU,max，并学习绘制单向等增益圆 和 等回波损耗圆。
- 重要提示 ：实际上，对于一个给定的增益值，其对应的输入反射系数是确定的。因此，等增益圆和等回波损耗圆本质上是同一个圆在史密斯图上的不同表达，知道其中一个就能推导出另一个。
双向性设计（Bilateral Case）：
- 前提：承认晶体管的双向性，即S12≠0S_{12} \neq 0S12=0。这是准确且推荐的正规设计方法。
- 设计内容 ：我们将学习如何在双向情况下求解最大可用增益GmaxG_{max}Gmax，并绘制 双向等增益圆 、可用功率增益圆GAG_AGA 和 功率增益圆GPG_PGP。这些圆图为我们在增益、噪声、功率和匹配之间进行权衡提供了直观的工具。

单向化设计

虽然不推荐使用，但理解单向化假设下的模型有助于厘清概念。

单向化增益GTUG_{TU}GTU

假设 S12=0S_{12} = 0S12=0。这意味信号只能正向传输，没有内部反馈。在此假设下，稳定因子K→∞K \to \inftyK→∞，晶体管无条件稳定。
输入/输出阻抗 ：输入反射系数简化为Γin=S11\Gamma_{in} = S_{11}Γin=S11，输出反射系数简化为Γout=S22\Gamma_{out} = S_{22}Γout=S22。因为不存在反馈路径，负载和源的变化不会相互影响。
增益分解 ：转换功率增益GTG_TGT可完美分解为三个独立部分的乘积（dB值为加和）：
GTU=GS×∣S21∣2×GLG_{TU} = G_S \times |S_{21}|^2 \times G_LGTU=GS×∣S21∣2×GL

其中：
GS=1−∣ΓS∣2∣1−S11ΓS∣2G_S = \frac{1 - |\Gamma_S|^2}{|1 - S_{11}\Gamma_S|^2}GS=∣1−S11ΓS∣21−∣ΓS∣2， 只与源匹配 ΓS\Gamma_SΓS有关。
∣S21∣2|S_{21}|^2∣S21∣2，是晶体管的本征增益。
GL=1−∣ΓL∣2∣1−S22ΓL∣2G_L = \frac{1 - |\Gamma_L|^2}{|1 - S_{22}\Gamma_L|^2}GL=∣1−S22ΓL∣21−∣ΓL∣2， 只与负载匹配 ΓL\Gamma_LΓL有关。

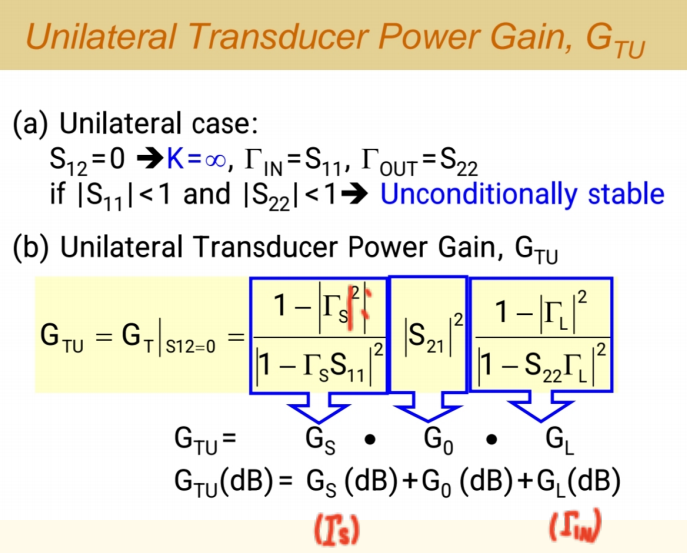
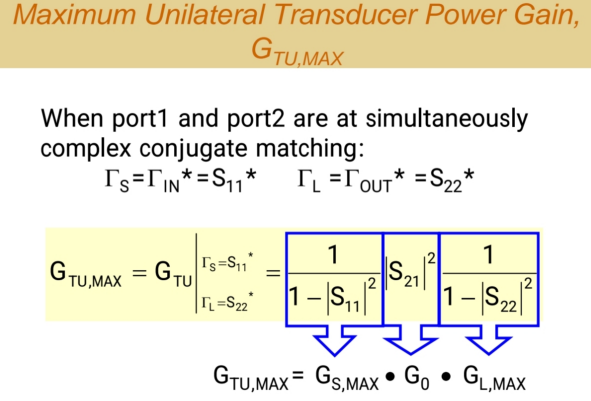
最大单向化增益GTU,maxG_{TU,max}GTU,max

最大增益 ：当输入(Port1)和输出(Port2)均实现共轭匹配ΓS=S11∗\Gamma_S = S_{11}^*ΓS=S11∗，ΓL=S22∗\Gamma_L = S_{22}^*ΓL=S22∗时，获得最大单向化增益：
UTU,max=11−∣S11∣2×∣S21∣2×11−∣S22∣2U_{TU,max} = \frac{1}{1 - |S_{11}|^2} \times |S_{21}|^2 \times \frac{1}{1 - |S_{22}|^2}UTU,max=1−∣S11∣21×∣S21∣2×1−∣S22∣21

等增益圆

等增益圆 ：如果我们不追求最大增益UmaxU_{max}Umax，而是一个更低的增益值 (G)，那么满足该增益条件的ΓS\Gamma_SΓS 和ΓL\Gamma_LΓL在史密斯圆图上会分别构成一个圆，即等增益圆 。这些圆直观地显示了为达到特定增益，源端或负载端可以选择的匹配点范围。

对于输入等增益圆，其圆心和半径的公式是已知的，如下图所示:

画输入增益圆的关键在于参数gSg_SgS归一化源增益

归一化的目的是保证输入增益圆的半径不会超过1，其取值范围从1到0。

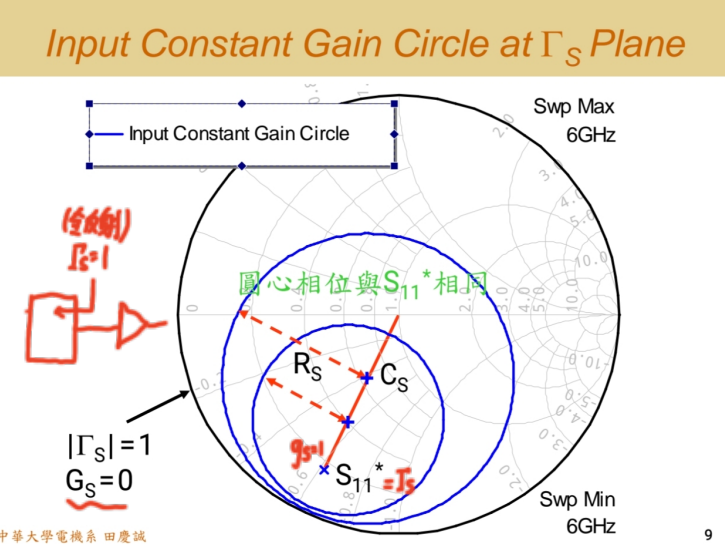
当gS=1g_S = 1gS=1 时 ：圆收缩为一个点，这个点就是ΓS=S11∗\Gamma_S = S_{11}^*ΓS=S11∗。这代表了源端实现共轭匹配，此时源增益GSG_SGS达到理论最大值1/(1−∣S11∣2)1/(1 - |S_{11}|^2)1/(1−∣S11∣2)。
当gSg_SgS逐渐减小时 ：圆的半径会越来越大 。圆上的每一个点ΓS\Gamma_SΓS都对应着相同的 、更低的源增益GSG_SGS。因此，这个圆的物理意义在于：如果你想获得一个特定的、低于最大值的增益，你有无限多种源匹配方式ΓS\Gamma_SΓS的选择，它们都落在同一个圆上。
当gS=0g_S = 0gS=0时 ：圆心位于原点，半径等于1。这是一个覆盖整个史密斯圆图的"最大圆"。在这个圆上（即所有可能的ΓS\Gamma_SΓS，源增益 (GS=0G_S = 0GS=0)。什么时候源增益为零？就是当∣ΓS∣=1|\Gamma_S| = 1∣ΓS∣=1，即发生全反射时。信号完全被反射回去，没有功率进入晶体管，增益自然为零。

同理，我们也可以为输出端绘制负载(输出)等增益圆 。

参数gLg_LgL归一化负载增益的取值范围也是从1到0。圆心和半径公式类似，但这些圆是画在ΓL\Gamma_LΓL的复平面上。

同理，画输出增益圆的关键在于参数gLg_LgL（归一化源增益），其取值范围从1 到 0。

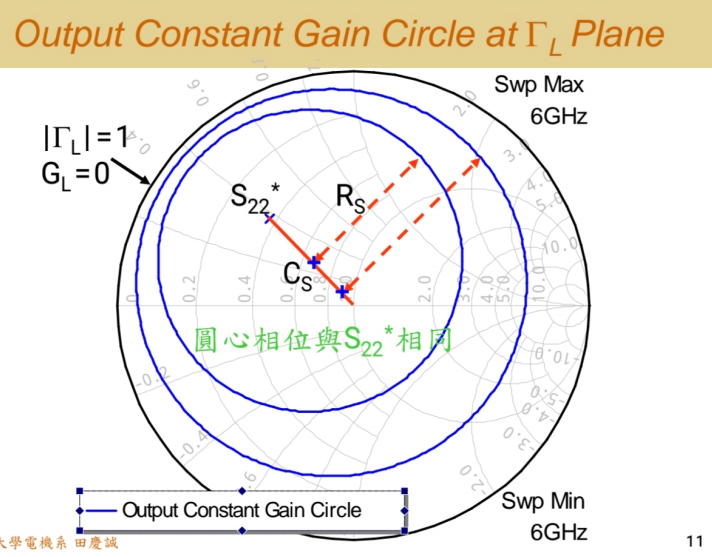
gL=1g_L = 1gL=1 时对应点ΓL=S22∗\Gamma_L = S_{22}^*ΓL=S22∗，输出共轭匹配，负载增益最大。
gLg_LgL减小时，圆半径增大，代表了为获得特定负载增益可供选择的ΓL\Gamma_LΓL的轨迹。
gL=0g_L = 0gL=0时，圆覆盖整个图，对应∣ΓL∣=1|\Gamma_L| = 1∣ΓL∣=1（全反射，无功率输出）。

工程实践要点 ：圆心和半径的具体公式并不需要记忆，因为所有仿真软件（如ADS、Cadence）都能自动计算和绘制这些圆。工程师的核心技能是理解这些圆的含义并学会使用软件工具。

单向化假设的陷阱：U因子判据

单向化设计看似简单，但它基于一个危险的假设：S12=0S_{12} = 0S12=0。而我们说大多数晶体管其实都不满足这个条件，所以并不能使用这个方法。但在某些情况下，晶体管近似单向，那我们就可以通过这种方法，简单迅速的设计出我们想要的输入输出匹配网络。

那么，问题的关键在于，我们如何判断一个晶体管在某个频率下是否"足够接近"单向，从而可以使用这种近似方法呢？

为此，我们引入一个关键指标：单向化优质因数（Unilateral Figure of Merit） ，记为 U 。

其计算公式为：
U=∣S12∣∣S21∣∣S11∣∣S22∣(1−∣S11∣2)(1−∣S22∣2)U = \frac{|S_{12}||S_{21}||S_{11}||S_{22}|}{(1 - |S_{11}|^2)(1 - |S_{22}|^2)}U=(1−∣S11∣2)(1−∣S22∣2)∣S12∣∣S21∣∣S11∣∣S22∣

它量化了使用单向化近似（计算增益GTUG_{TU}GTU，与使用精确双向公式（计算增益GTG_TGT之间的最大可能误差 。

实际增益GTG_TGT被限制在以下范围：
GTU(1+U)2<GT<GTU(1−U)2\frac{G_{TU}}{(1+U)^2} < G_T < \frac{G_{TU}}{(1-U)^2}(1+U)2GTU<GT<(1−U)2GTU

（在dB尺度上，表现为正负某个dB值的误差带）。

如何解读U因子：

U 越小：误差范围越窄，单向化近似越准确，实际增益与近似增益非常接近。
U 越大：误差范围越宽，使用单向化近似会导致很大的设计误差，结果不可靠。

一个常见的误解是：低频时S12S_{12}S12很小，因此晶体管在低频更像单向元件。然而，事实可能恰恰相反。

我们来观察晶体管BFP240它的频率特性曲线：

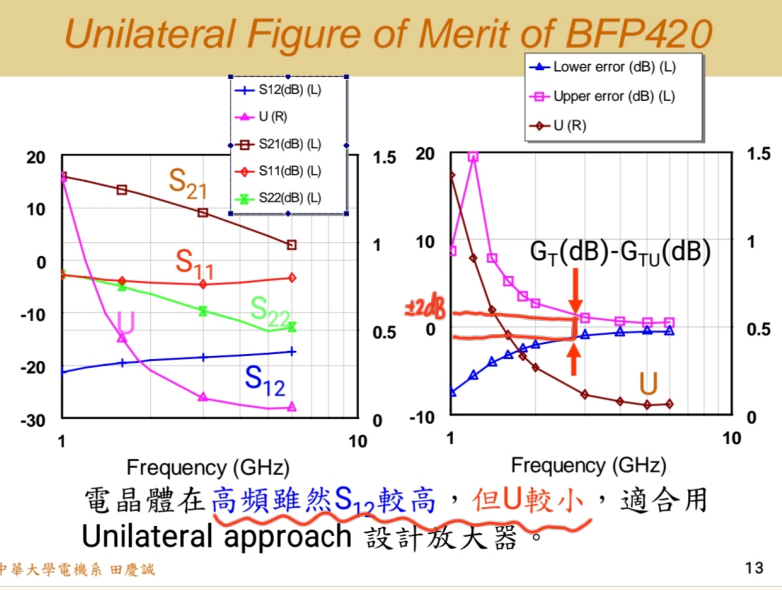
S21S_{21}S21（正向增益）：随频率升高而下降（受寄生电容影响）。
S12S_{12}S12（反向隔离）：随频率升高而上升（也是寄生电容的耦合路径），但在很高频时会趋于平缓，不再急剧增加。
通过实际计算U因子随频率变化的曲线，我们经常发现：在高频区域，U因子反而更小 。这是因为尽管高频时S12S_{12}S12的绝对值可能不小，但 S21S_{21}S21下降得更快，且S11S_{11}S11和S22S_{22}S22的匹配情况也在变化，综合作用下使得U值减小。这意味着，晶体管在高频时可能更适合采用单向化近似，而在中低频段误差可能更大。
补充：为什么S12S_{12}S12在高频会趋于平缓，而不是无限增大？
这需要从晶体管内部的寄生反馈机制理解。
在很高频率下，主要的反馈路径通过基极-集电极电容CbcC_{bc}Cbc（或栅漏电容 CgdC_{gd}Cgd等寄生元件。当频率极高时，这些电容的阻抗变得很小，使得输入和输出端近乎"直通"。此时，从输出到输入的电压传输系数会趋近于一个由内部电阻分压决定的稳态值（通常远小于1），而不是持续增加。
因此S12S_{12}S12的曲线会饱和平缓。而S21S_{21}S21由于跨导随频率下降以及输出节点电容的影响，会持续滚降。这一升一降的动态关系，是造成U因子高频变小的内在原因。

工程启示 ：

这解释了为什么有些工程师"碰巧"用简单的单向匹配ΓS=S11∗\Gamma_S = S_{11}^*ΓS=S11∗，ΓL=S22∗\Gamma_L = S_{22}^*ΓL=S22∗也能做出性能尚可的放大器------他们很可能恰好选在了U值很小的频点上工作。但这是一种依赖运气的"土法炼钢"。正规且可靠的设计流程应该是：

在设计频率点计算U因子。
如果U值足够小（例如，带来的增益误差 < 1 dB），可以考虑使用单向化设计以简化流程。
如果U值较大，必须使用严格的双向性设计方法，并借助等增益圆等工具进行综合。

等增益圆与等回波损耗圆

有些仿真软件（如ADS）提供等增益圆(Constant Gain Circle) 功能，有些仿真软件如MicroOffice，则只提供 等回波损耗圆（Constant Return Loss Circle） 。但这两种圆本质上描述的是同一个物理现象，只是表现形式不同。

为什么它们是等价的？我们需要理解其中的关联：

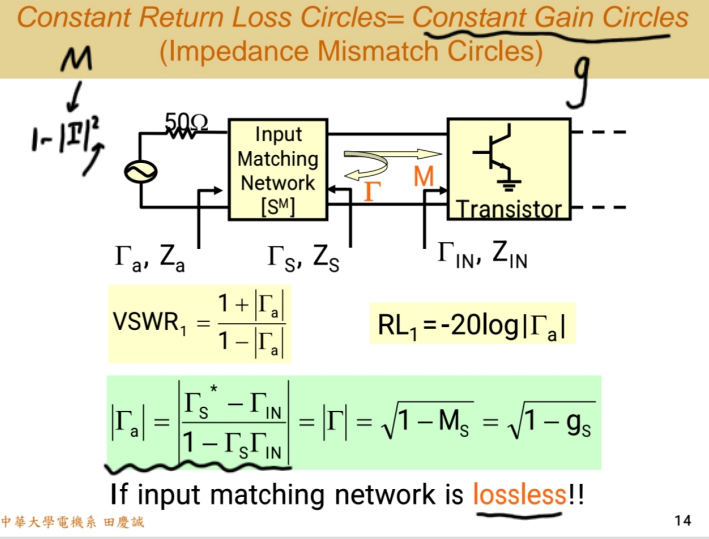
增益（Gain） 的下降源于 失配（Mismatch） 导致的功率损失。归一化增益ggg通常定义为实际增益与理想最大增益的比值。在阻抗匹配的理想情况下，g=1g=1g=1；当存在失配时，ggg下降。若仅考虑功率损失（忽略相位影响 ），ggg和MMM的关系可表示为： g=M g = M g=M
失配因子MMM 与 反射系数Γ\GammaΓ 有确定关系：M=1−∣Γ∣2M = 1 - |\Gamma|^2M=1−∣Γ∣2。失配越大，反射系数模值越大。
当|Γ| = 0时，表示完全匹配，无反射，此时M = 1。
当|Γ| = 1时，表示完全失配，全反射，此时M = 0。
因此，给定一个归一化增益 (g)（或失配 (M)），就确定了一个对应的反射系数模值∣Γ∣|\Gamma|∣Γ∣。
而一个恒定的反射系数模值 ∣Γ∣|\Gamma|∣Γ∣，在史密斯圆图上就是一个圆------这就是等回波损耗圆 或等VSWR圆 。
所以，等增益圆、等失配圆、等回波损耗圆和等VSWR圆，它们在史密斯圆图上画出来是同一个圆。软件可能只提供其中一种，但工程师需要理解它们的等价性，并能通过简单换算进行互认。

这里还有一个非常有用的物理现象，在前面的匹配网络分析中已经证明过：对于一个无损（Lossless） 的匹配网络，网络两端的 稳态反射系数的模值 是完全相同的（仅相位不同）。这意味着：

从匹配网络输入端看进去的反射系数ΓA\Gamma_AΓA，其模值等于从晶体管输入端看进去的反射系数Γin\Gamma_{in}Γin或 (S_{11}) 的稳态效应的模值。
因此，我们可以通过分析匹配网络输入端的反射要求 ，直接推断出源匹配点ΓS\Gamma_SΓS的选择范围。这个关系在进行系统级分析（如评估天线、滤波器、放大器级联后的整体性能时至关重要。

工程稳健性

现在，面对软件画出的等回波损耗圆（例如Return Loss = 10 dB, 对应图中紫色的圆，Return Loss = 5 dB,对应图中蓝色的圆）

真正的工程问题来了：圆上有无数个点ΓS\Gamma_SΓS都能满足相同的回波损耗要求，我究竟该选哪一个？

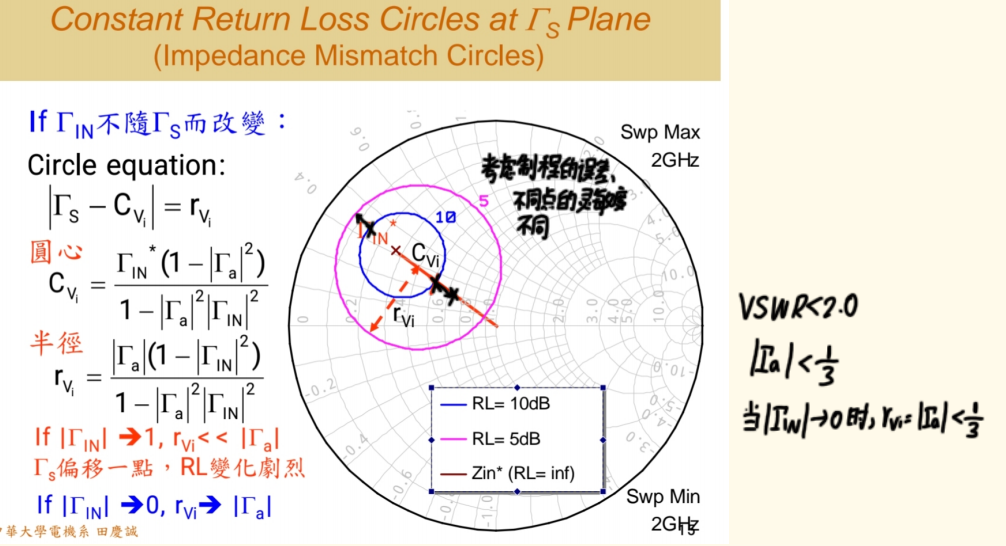
答案并非是我们想怎么选怎么选，而是要基于设计对制造误差和环境变化的鲁棒性Robustness进行选择。我们可以将等回波损耗圆看作一张"等高线地图"：

密集区域（圆上较"陡峭"的部分） ：在这些点附近，反射系数对 (ΓS\Gamma_SΓS) 的微小变化极为敏感。也就是说，如果实际元件值（电感、电容）因工艺偏差、温度变化或老化而略有偏移，ΓS\Gamma_SΓS 会迅速偏离设计点，导致回波损耗急剧恶化（例如从10 dB骤降到5 dB）。
稀疏区域（圆上较"平缓"的部分）：在这些点附近，同样的元件值偏差只会引起反射系数的微小变化，回波损耗保持稳定。
为了确保产品在大批量生产中的一致性和长期可靠性，我们必须选择圆上最稀疏、最平缓的区域 作为设计点。这通常对应着 ΓS\Gamma_SΓS的实部较大、接近实数阻抗的区域。

进一步分析等回波损耗圆圆心和半径的公式，我们可以得到更深层次的洞察------圆心位置与晶体管的 S11S_{11}S11或更精确地说，稳态Γin\Gamma_{in}Γin直接相关。

当Γin\Gamma_{in}Γin或 S11S_{11}S11接近圆心（即模值很小时：
- 公式显示，此时等回波损耗圆的半径 rVir_{Vi}rVi近似等于所允许的反射系数模值∣ΓA∣|\Gamma_A|∣ΓA∣。
- 这意味着，如果晶体管本身的输入端口匹配良好S11S_{11}S11很小，那么为满足系统VSWR要求（例如，若要求VSWR < 2，∣ΓA∣|\Gamma_A|∣ΓA∣ < 1/3），你选择的 ΓS\Gamma_SΓS只需落在以S11S_{11}S11 为中心、半径为1/31/31/3的圆内即可。可选范围很大，设计灵活性高，且对误差不敏感。
当Γin\Gamma_{in}Γin或S11S_{11}S11模值很大（接近圆图边缘时：
- 情况变得严峻。即使你仍然要求系统输入端 ∣ΓA∣<1/3|\Gamma_A| < 1/3∣ΓA∣<1/3，但由于S11S_{11}S11本身很差，ΓS\Gamma_SΓS的选择范围会急剧缩小，只剩下圆图边缘一个很小的弧段。
- 在这种区域设计匹配网络，ΓS\Gamma_SΓS的允许范围极窄，对元件值的任何微小偏差都极其敏感。这相当于在悬崖边上行走，匹配网络的 Q 值会非常高，导致工作带宽极窄，且性能对工艺、温度等变化极为脆弱。

这些分析给我们带来了宝贵的工程启示：

优选器件 ：在项目初期选择晶体管时，应优先考虑S11S_{11}S11和 S22S_{22}S22模值较小的器件。这样的器件不仅本身容易匹配，而且允许的源/负载匹配点范围宽，能设计出对误差不敏感、鲁棒性强的放大器。
警惕高Q值设计：如果一个设计迫使你必须在史密斯圆图的边缘区域选取匹配点，这通常意味着匹配网络的 Q 值极高，带宽极窄。这样的设计在生产中极难控制，良率低，应尽力避免。
从图形到本质：阅读史密斯圆图上的等值线时，不能只看它"是什么"（例如，10 dB回波损耗圆），更要看懂它"为什么是这样"（圆心、半径与器件参数的关系），并判断"哪里是安全区"（稀疏、平坦区域）。这种能力将理论分析与工程实践紧密结合起来。

实际例子

我们接下来通过一个具体的设计范例，来实际操作如何利用单向化等增益圆（或等回波损耗圆）来设计一个放大器，并深入评判这种方法的优劣。

第一步：明确设计约束

许多教科书范例往往只关注如何实现某个增益，而忽略了关键的系统级要求。在实际工程中，第一优先级永远是满足系统规范。我们首先设定明确的设计约束：

目标：设计一个放大器。
核心指标 ：输入/输出端的电压驻波比 VSWR < 2.0（这是一个非常常见的系统要求）。
指标换算 ：
- VSWR < 2.0 等价于反射系数模值 ( ∣Γ∣<1/3|\Gamma| < 1/3∣Γ∣<1/3 )。
- 回波损耗 Return Loss > 10.5 dB（近似取 10 dB 作为设计目标）。
- 对应的失配因子 (M=1−∣Γ∣2=8/9M = 1 - |\Gamma|^2 = 8/9M=1−∣Γ∣2=8/9 )。

这个系统要求直接限制了放大器的潜在增益！

源端和负载端的归一化增益 (gSg_SgS) 和 (gLg_LgL)的最大值只能是 (M = 8/9)（约 -0.51 dB）。
因此，即使晶体管本身能提供很高的本征增益∣S21∣2|S_{21}|^2∣S21∣2，为了满足VSWR要求，从源和负载端"贡献"的增益 gSg_SgS和 gLg_LgL各自最多损失约0.5 dB。
总增益上限 ：GTU,maxG_{TU, max}GTU,max(受VSWR约束) ≈ ∣S21∣2|S_{21}|^2∣S21∣2 - 1.02 dB。无法在不恶化VSWR的情况下获得更高的增益。

课本上让你"随意"选择一个增益值进行设计是不合理的。真正的设计增益范围，从一开始就被系统对端口匹配（VSWR）的要求所严格限定。

第二步：选择器件与评估单向化近似误差

根据工作频率和所需的增益范围，我们选择了一款合适的晶体管。假设其参数如下：

在目标频率（例如3 GHz）下，最大单向化增益 UTU,maxU_{TU,max}UTU,max = 11.4dB。
计算单向化优质因数 U = 0.12。
误差评估 ：根据U值，可以估算出使用单向化近似设计的增益 (( GTUG_{TU}GTU )) 与真实增益GTG_TGT之间的误差范围大约在 ±1 dB 以内 。这个误差在工程上是可以接受的，因此我们暂时可以采用单向化方法进行初步设计。
设定设计目标增益 ：考虑到VSWR约束带来的1 dB损耗，我们的目标增益设定为GTU≈10.38dBG_{TU} \approx 10.38dBGTU≈10.38dB,画10.5dB的等增益圆。

第三步：利用等回波损耗圆进行匹配点选择

我们不再直接使用等增益圆，而是使用与之等价的等回波损耗圆 （例如，10 dB Return Loss圆，对应 ∣Γ∣=1/3|\Gamma| = 1/3∣Γ∣=1/3。

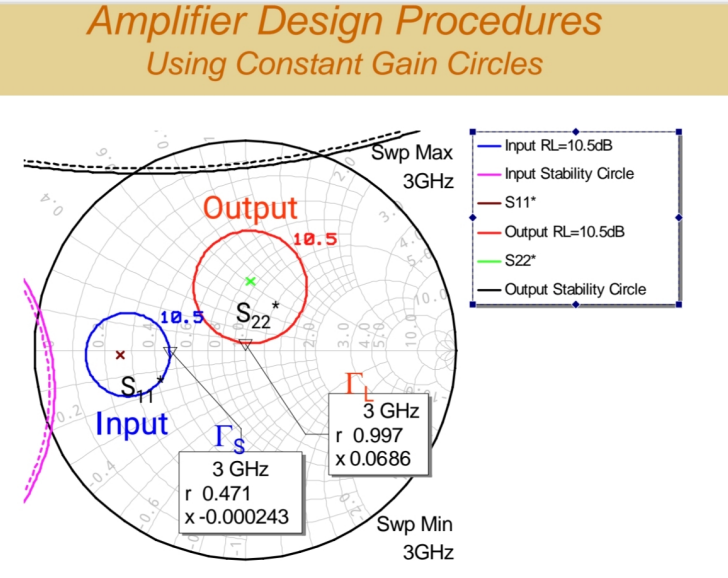
绘制圆圈 ：在史密斯圆图上，分别绘制输入端的等回波损耗圆（在ΓS\Gamma_SΓS平面）和输出端的等回波损耗圆（在ΓL\Gamma_LΓL平面）。圆心分别与 S11S_{11}S11和S22S_{22}S22有关。
选择匹配点 ΓS\Gamma_SΓS和 ΓL\Gamma_LΓL ：圆上的任何一点都能满足10 dB的回波损耗要求。但选择哪一点至关重要。
- 稳定性考量 ：即使假设S12=0S_{12}=0S12=0，我们仍需检查潜在不稳定区域,应选择远离不稳定区的点。
- 设计简便性与鲁棒性 ：观察输出端的圆，我们发现有一点非常接近50Ω点（史密斯圆图中心）。这意味着如果我们选择ΓL\Gamma_LΓL为这一点，输出端几乎不需要进行匹配网络，可以近似直接连接50Ω负载。这极大地简化了设计。
- 因此，我们选择：
  - ΓL\Gamma_LΓL：接近50Ω的点（简化输出匹配）。
  - ΓS\Gamma_SΓS：在输入等回波损耗圆上，选择一个便于实现、且远离不稳定区域的点（通常选择阻抗实部较大、变化平缓的区域）。

第四步：设计匹配网络与仿真验证

根据选定的ΓS\Gamma_SΓS，我们从50Ω出发，往后退，使用串联/并联电感/电容，在史密斯圆图上将阻抗"推移"到目标点，从而设计出输入匹配网络。输出端因 ΓL≈0\Gamma_L \approx 0ΓL≈0，可暂不匹配。

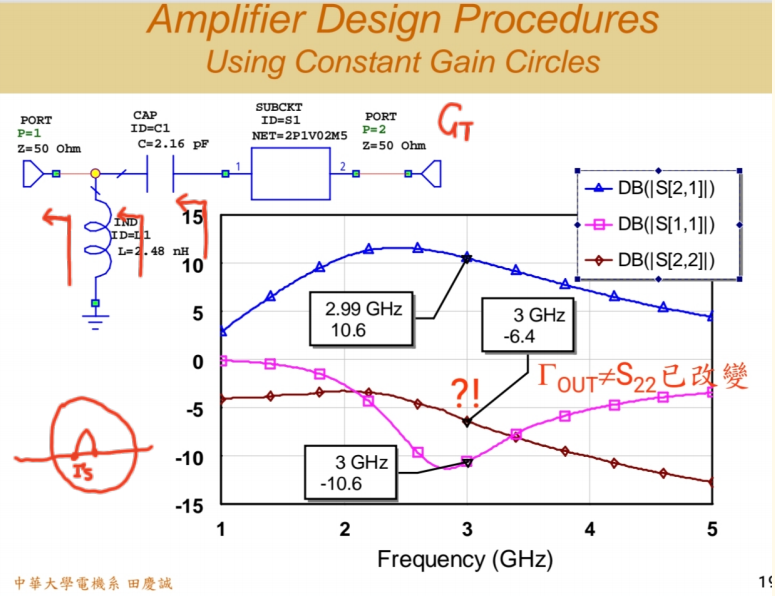
将设计好的电路进行仿真,在50Ω源和负载条件下，得到以下结果：

增益GTG_TGT(S21S_{21}S21) ：仿真结果为 10.6 dB，与我们理论设定的目标10.4 dB非常接近，误差仅0.2 dB。这证明了单向化近似在本例中的有效性。
输入回波损耗S11S_{11}S11：仿真结果良好，接近-10 dB的设计目标。
输出回波损耗S22S_{22}S22 ：仿真结果很差，只有约 -6 dB，远未达到-10 dB的目标。

第五步：深度问题分析------单向化设计的根本缺陷

为什么S22S_{22}S22会失败？这正是单向化设计方法的缺陷。

输入端成功（运气好）的原因 ：我们为输入端设计了匹配网络，将ΓS\Gamma_SΓS匹配到了预定点。由于输出端我们没有添加匹配网络，因此从晶体管输出端看进去的负载就是50Ω。在单向化假设下 S12=0S_{12}=0S12=0，输出负载的变化不会影响输入阻抗 。所以，我们设计好的输入匹配得以保持，S11S_{11}S11表现良好。
为了让输出匹配，应该让负载ΓLΓ_LΓL等于晶体管输出反射系数 Γout∗Γ_{out}^*Γout∗ ,但是，我们为输出端选择的ΓL\Gamma_LΓL是基于一个错误的假设 ：即认为从晶体管输出端看进去的反射系数 Γout\Gamma_{out}Γout等于其自身的S22S_{22}S22。
这个等式只在S12=0S_{12}=0S12=0时才严格成立 。
- 实际上，Γout=S22+S12S21ΓS1−S11ΓS\Gamma_{out} = S_{22} + \frac{S_{12}S_{21}\Gamma_S}{1 - S_{11}\Gamma_S}Γout=S22+1−S11ΓSS12S21ΓS。
- 当我们为输入端添加了匹配网络（改变了ΓS\Gamma_SΓS，这个ΓS\Gamma_SΓS会通过晶体管的内部反馈S12S_{12}S12显著影响Γout\Gamma_{out}Γout。
- 因此，我们之前为输出端选择的、旨在匹配那个错误的ΓoutΓ_{out}Γout的负载ΓLΓ_LΓL，现在面对的是一个受前端匹配网络影响而改变了的 、真实的ΓoutΓ_{out}Γout。二者完全不匹配，导致最终的输出端口匹配S22S₂₂S22性能很差.

这个范例清晰地展示了单向化设计方法的严重局限性 ：它是一个"解耦"的、看似简单的模型，但一旦你开始为任何一端添加真实的匹配电路，另一端的设计就会因为被忽略的反馈S12S_{12}S12而崩溃。你不得不陷入"拆东墙补西墙"的反复调试中。

许多工程师凭经验"调"出一个能用的设计，往往是偶然触碰到了那个唯一的、精确的双向共轭匹配解（即ΓS=Γin∗\Gamma_S = \Gamma_{in}^*ΓS=Γin∗，ΓL=Γout∗\Gamma_L = \Gamma_{out}^*ΓL=Γout∗。但这个过程低效且不可靠。

更优的正规方法 ：我们应该直接采用双向性设计，求解最大可用增益 ( G_{max} ) 及其对应的唯一匹配点 ( (\Gamma_{S, opt}, \Gamma_{L, opt}) )。这个解同时优化了增益和端口匹配（( S_{11} ) 和 ( S_{22} )），避免了单向化方法的内在矛盾。这才是高效、可靠的工程设计流程。

最简设计法：最大可用增益的唯一解

前面演示的单向化设计方法繁琐且效果不佳，常常需要反复调试S11S_{11}S11和 S22S_{22}S22。现在，我要教大家一个最简单、最正规 的放大器设计方法。

如果你想设计一个放大器，并且希望得到最大的增益（Gain） ，那么有一个唯一解 。这个解就是最大转换功率增益GTmaxG_{Tmax}GTmax（也常写作GmaxG_{max}Gmax。
只需要按照这个解去设计，就能同时实现前后端口的共轭匹配。记住，这里提升的是功率增益（Gain），而不是输出功率。输出功率的大小取决于晶体管的直流工作点和负载线（DC-IV曲线），与最大增益匹配是两回事。

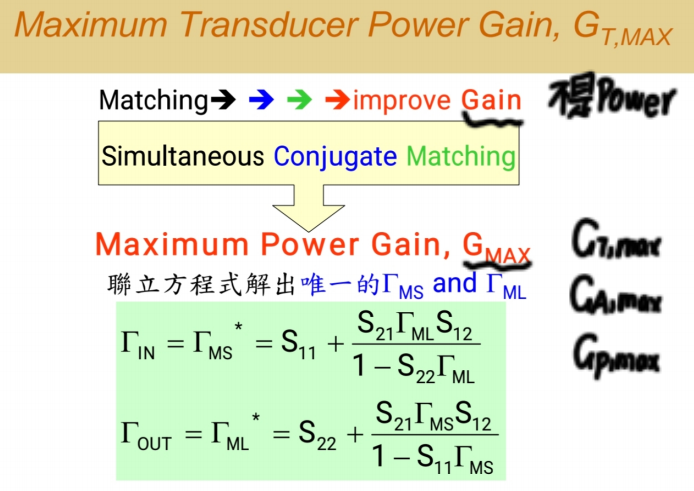
这个唯一解由以下方程定义：

(ΓS=Γin∗\Gamma_S = \Gamma_{in}^*ΓS=Γin∗)
(ΓL=Γout∗\Gamma_L = \Gamma_{out}^*ΓL=Γout∗)

其中：

(Γin=S11+S12S21ΓL1−S22ΓL\Gamma_{in} = S_{11} + \frac{S_{12}S_{21}\Gamma_L}{1 - S_{22}\Gamma_L}Γin=S11+1−S22ΓLS12S21ΓL)
(Γout=S22+S12S21ΓS1−S11ΓS\Gamma_{out} = S_{22} + \frac{S_{12}S_{21}\Gamma_S}{1 - S_{11}\Gamma_S}Γout=S22+1−S11ΓSS12S21ΓS)

这里有两个方程和两个未知数ΓS\Gamma_SΓS和ΓL\Gamma_LΓL，因此可以解出唯一的一组解，我们称之为ΓS,opt\Gamma_{S,opt}ΓS,opt和ΓL,opt\Gamma_{L,opt}ΓL,opt。

注意：如果解出来的反射系数模值 > 1 ，那这个解在物理上是无法实现的（因为无源匹配网络无法产生∣Γ∣>1|\Gamma| > 1∣Γ∣>1的点），我们只能舍弃。什么情况下会出现这种无解呢？

这个唯一解存在的 充分必要条件 ，正是我们反复强调的：晶体管必须绝对稳定，即稳定因子 K > 1 且∣Δ∣<1|\Delta| < 1∣Δ∣<1。

这完美解释了为什么我们设计的第一步 总是先稳定晶体管 。只有当 K > 1 时，那个理想的、能同时最大化增益并完美匹配端口S11S_{11}S11和S22S_{22}S22接近0）的唯一解才存在，并且是物理可实现的∣ΓS,opt∣<1,∣ΓL,opt∣<1|\Gamma_{S,opt}| < 1, |\Gamma_{L,opt}| < 1∣ΓS,opt∣<1,∣ΓL,opt∣<1

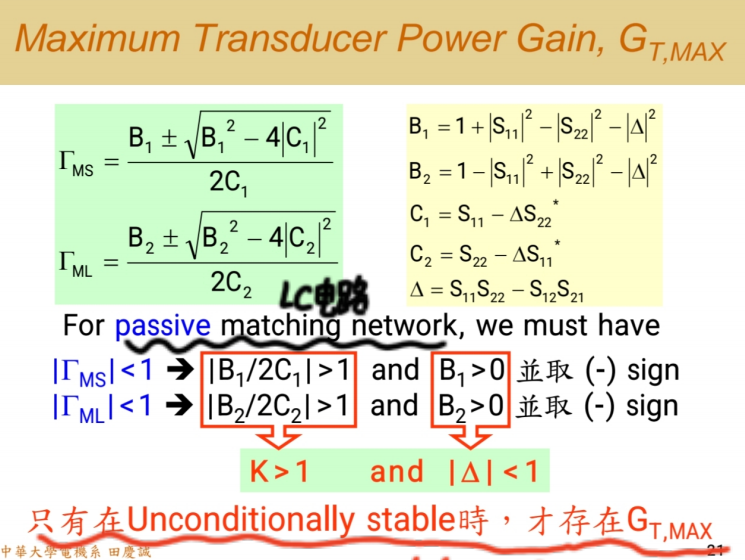
在工程实践中，我们根本不需要手动记忆或推导复杂的求解公式。所有射频仿真软件（如ADS、Cadence）都内置了这个求解功能 。你只需要输入晶体管的S参数，软件会瞬间（不到一秒）计算出 GmaxG_{max}Gmax、ΓS,opt\Gamma_{S,opt}ΓS,opt 和ΓL,opt\Gamma_{L,opt}ΓL,opt(两个复数解)。

PS：

如果给的是晶体管的模型model,ADS 同样可以处理。

给模型后，还需要设定偏置点（Bias Point）。软件会在这个偏置下进行交流（AC）小信号分析 ，从而计算出小信号的 S 参数。

要注意：ADS 的"小信号分析"假设信号是无限小 的。但实际用网络分析仪测量晶体管 S 参数时，如果输入功率是 0dBm（这已经不小了），可能就不算"小信号"了，通常需要设置为 -20 dBm 或 -30 dBm才合适。所以，测量时输入的功率必须足够小，才能和 ADS 的小信号模拟结果对应上。
关于大信号 S 参数的知识： 我们刚才讨论的都是小信号 S 参数。但在大信号工作时（比如功率放大器），晶体管的特性会随输入功率和偏压点变化，此时 S 参数不再是固定的，这就引入了大信号S参数的概念。

在 ADS 中进行大信号模拟时，你需要指定输入功率的大小。对于给定的功率和偏压，会对应一组 S参数。这比小信号模型复杂得多，因为它包含了非线性效应。对于功率放大器、混频器等非线性电路的设计，有时会用到这种方法。

不过，使用大信号 S参数模拟的人并不多，因为它比较复杂，而且准确度也面临挑战：你需要提供足够多、覆盖不同功率和偏压点的数据，模型本身也要足够精确。所以，它通常是介于理想小信号模型和完全非线性模型之间的一种折中方法，其准确性仍需谨慎评估。

设计过程因此变得极其高效：稳定化（如果需要）→ 软件求解 → 根据ΓS,opt\Gamma_{S,opt}ΓS,opt和ΓL,opt\Gamma_{L,opt}ΓL,opt设计匹配网络 → 完成。

PS:
方向千万不能搞错 ，这是学习放大器的核心重点,一旦搞错,全盘皆输。 ΓS,opt\Gamma_{S,opt}ΓS,opt是往哪边看？是往源端方向看 。最前边是 50

欧姆的源阻抗，往后是输入匹配电路。从晶体管输入端看进去，整个源端呈现的反射系数应该是 ΓSΓ_SΓS。

ADS 帮你算出的ΓS,opt(Γms)\Gamma_{S,opt}(\Gamma_{ms})ΓS,opt(Γms)，意思就是你需要设计一个输入匹配网络 ，使得从晶体管输入端向左看，看到的就是(Γms)(\Gamma_{ms})(Γms)。软件给了你答案，接下来就需要你"自己动手"把这个匹配电路做出来。

同样，(Γml)(\Gamma_{ml})(Γml)是往负载端方向看。你的负载最终也要接到 50 欧姆。ADS

解出(Γml)(\Gamma_{ml})(Γml)后，你就需要设计一个输出匹配网络 ，使得从晶体管输出端向右看，看到的就是(Γml)(\Gamma_{ml})(Γml)

最大增益的表达式与K值的关系

在绝对稳定条件下，最大增益 (G_{max}) 有一个简洁的表达式：
Gmax=∣S21∣∣S12∣(K−K2−1)G_{max} = \frac{|S_{21}|}{|S_{12}|} \left( K - \sqrt{K^2 - 1} \right)Gmax=∣S12∣∣S21∣(K−K2−1 )

这个公式清晰揭示了GmaxG_{max}Gmax与稳定因子 (K) 的关系：

当 K = 1 时 ：Gmax=∣S21∣∣S12∣G_{max} = \frac{|S_{21}|}{|S_{12}|}Gmax=∣S12∣∣S21∣，这个值恰好等于 MSG（最大稳定增益）。
当 K > 1 时 ：随着 K 增大，括号内的值(K−K2−1)(K - \sqrt{K^2 - 1})(K−K2−1 )会减小。这意味着，K 值越大，你能获得的最大增益GmaxG_{max}Gmax反而越低。

关键的工程权衡：稳定性裕度 vs. 增益 vs. 设计灵敏度

这引出了一个重要的工程权衡：我们是否应该追求极限的 K=1，以获得理论上的最高增益（MSG）？

答案是否定的，这非常危险！

灵敏度与鲁棒性 ：当 K 非常接近于 1 时，计算出的最佳匹配点 ΓS,opt\Gamma_{S,opt}ΓS,opt和ΓL,opt\Gamma_{L,opt}ΓL,opt会非常靠近稳定圆的边界。这意味着，实际电路中元件的微小偏差（容差、温度漂移、寄生效应）很容易使工作点滑入不稳定区域，导致振荡或性能急剧恶化。你的设计会变得极其脆弱。
匹配难度：此时的匹配点通常在史密斯圆图上远离中心，意味着匹配网络需要很高的电抗（高Q值），难以实现且带宽很窄。
牺牲少量增益换取稳健性 ：因此，在工程上我们宁愿牺牲一点增益 ，通过稳定性电路（如并联电阻）将 K 值提高到 1.1 左右。虽然GmaxG_{max}Gmax会下降到比 MSG 低约 1-2 dB，但换来的是：
- 最佳匹配点移向圆图中心区域，匹配更容易、更宽频。
- 系统对元件变化和环境变化的 鲁棒性（Robustness）大大增强。
- 这正是为什么许多实践经验规则会建议将工作增益设计在 MSG - 2 dB 附近，这背后是深刻的稳定性与可实现性的考量。

设计策略总结

所以，一个完整且稳健的放大器设计策略是：

评估与稳定化 ：检查晶体管在工作频段的稳定性。如果 K < 1，首先使用电阻等无源元件进行稳定化补偿，确保在整个频带内 K > 1（通常目标在1.1左右为宜）。
求解唯一解 ：利用软件求解绝对稳定条件下的GmaxG_{max}Gmax、ΓS,opt\Gamma_{S,opt}ΓS,opt和ΓL,opt\Gamma_{L,opt}ΓL,opt。
实现匹配 ：根据求解出的ΓS,opt\Gamma_{S,opt}ΓS,opt和 ΓL,opt\Gamma_{L,opt}ΓL,opt，设计输入和输出匹配网络。
关于增益过高 ：如果晶体管在某个频段的GmaxG_{max}Gmax过高（例如，超出了级联系统的需求，或可能引发稳定性问题），可以故意在该频段引入更多的电阻性损耗 ，从而进一步提高 K 值，主动将GmaxG_{max}Gmax降低到一个合适的水平。这正是"以可控的增益损失，换取确定性的稳定性和设计裕度"。

实际例子

我们以一颗 BF420 晶体管的仿真曲线为例。在给定的偏压下，软件计算出其 S 参数。

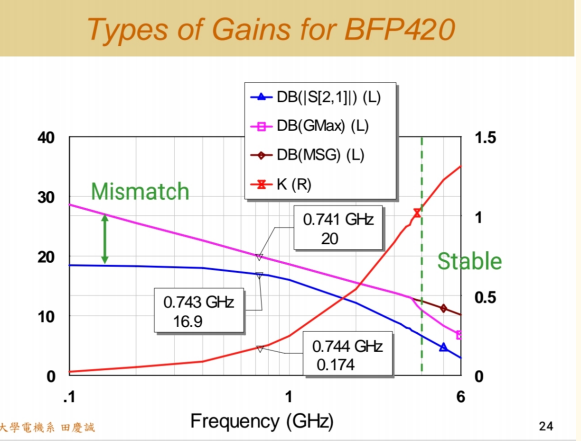
蓝线是 S21S_{21}S21（正向增益）。
粉红线 是计算出的 GmaxG_{max}Gmax（最大可用增益）。
注意看粉红线：在某一点突然出现一个很奇怪的尖峰或突变。这一点对应的就是 K = 1 的频率点。
- 在 K > 1 的区域，GmaxG_{max}Gmax曲线是平滑的（粉色线下半部分）。
- 在 K < 1 的区域，理论上的GmaxG_{max}Gmax公式会算出虚数（无物理意义），实际上意味着增益可以趋向无限大（即振荡），所以粉色的 Gmax 曲线在此区域其实没有意义。
咖啡色线 就是 MSG（最大稳定增益）。实际上，在 K < 1 的整个区域，这条咖啡色线都存在，只是在 K > 1 的区域被粉色的 Gmax 曲线覆盖了。
当我们拿到一颗晶体管的数据手册，或者仿真模型，必须立刻去计算它的 MSG 。它能告诉你，理论上这颗晶体管最多能提供多大的增益 。计算公式是：
MSG=∣S21∣∣S12∣MSG = \frac{|S_{21}|}{|S_{12}|}MSG=∣S12∣∣S21∣
怎么理解 MSG 的物理意义？ 课本的解释可能比较含糊：当 K < 1（潜在不稳定）时，无法实现前后同时共轭匹配（否则会振荡）。此时，我们定义 MSG 作为一个"安全"的增益上限。可以这样简单理解：它是在保证电路能够稳定工作（不振荡）的前提下，通过某种方法（例如只在输入或输出端进行匹配，而非两端同时匹配）所能获得的最大增益的近似值。

实验验证：

接下来我们用一个实验来证明上面讲的结论：稳定后的电路增益，不会超过原不稳定晶体管的 MSG。

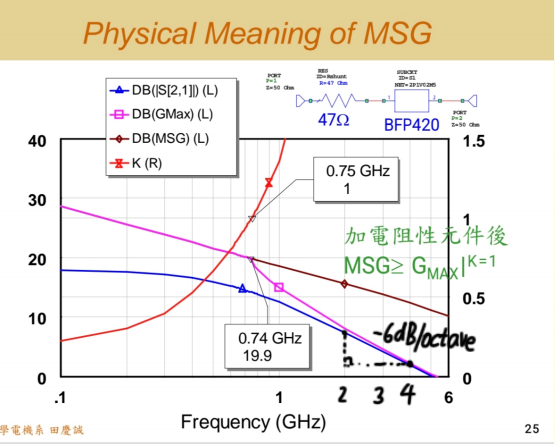
我们关注频率 741 MHz 这个点。原本K=0.174，MSG 是 20 dB.(请看上图)

通过串联一个 47 欧姆电阻 ，将这个频率点的 K 值提升到了 1。

观察结果：

红线（K值）在 750 MHz 附近被拉到了 1。
粉红线（新电路的GmaxG_{max}Gmax）在对应点被拉到了 MSG 曲线之下。
最关键的是：咖啡色的 MSG 曲线几乎没有变化！

实验结论 ：我通过加电阻，在 750 MHz 将 K 值从 0.174 提升到 1，得到了一个新的、稳定的GmaxG_{max}Gmax。但这个新的GmaxG_{max}Gmax绝对没有超过原来不稳定晶体管的 MSG（20 dB）。这就完美验证了之前的论断。

补充说明 ：

1.这个实验用的是串联电阻。你们可以回去自己试试并联电阻，结论类似。但如果使用反馈电阻 来稳定电路，情况会有所不同：即使同样把 K 值调到 1，最终能获得的增益可能会比 MSG 还低 ，而且整个增益曲线的形状会变得平坦许多。所以用反馈方式稳定电路要格外小心，它对增益的压制作用可能更强。

2.关于增益斜率（Roll-off）的经验：

图中 MSG 曲线在高频是下降的，这个斜率是多少？回忆我们很早讲过的晶体管增益特性：频率每增加一倍（一个 Octave），增益大约下降 6 dB。观察图中从 2 GHz 到 4 GHz（一个 Octave），MSG 确实下降了大约 6 dB。而 S21 曲线也有类似的斜率。

不过要注意，这个"6 dB/Octave"的经验规律，在 K > 1 的区域（即 GmaxG_{max}Gmax有效的区域）比较典型和准确。而在 K < 1 的 MSG 区域，斜率可能会缓一些。这需要大家多仿真、多观察，积累经验。

可用功率增益圆GAG_AGA

但我们设计放大器，未必就是为了使功率增益最大，而是有其它的设计目标，比如最小噪声或者最大功率输出，这就是我们接下来要涉及的两大内容。

首先我们研究的是"恒定可用功率增益圆"（Constant Available Power Gain Circle,在ADS里你们去找Ga,CircleG_{a,Circle}Ga,Circle。

我们先简单介绍一下它的理论。

首先，它最适合用来设计低噪声放大器（LNA） 。

为什么呢？因为它不需要前后级同时匹配 。它需要哪一级匹配？后级（输出端） 。那前级（输入端）呢？前级不需要匹配 ，甚至要故意失配（mismatch） 。

为什么？因为要抑制噪声。如果前级匹配太好，信号和噪声都会顺利进来并被放大，那噪声性能就完了。所以前级要故意失配来"阻挡"噪声（主要是实现最佳噪声匹配）。而后级的信号已经放大，不会再引入主要噪声，所以就做匹配，把增益提上来。

因此，GaG_aGa的设计精髓就在于：后级强制匹配，前级根据需求（这里是噪声）来设置 。GaG_aGa的公式就是在传输功率增益GTG_TGT的公式中，强制让后级匹配（ΓL=Γout∗Γ_L = Γ_{out}^*ΓL=Γout∗）后得到的简化形式。

关键点：

后级匹配条件 ：ΓLΓ_LΓL必须等于 Γout∗Γ_{out}^*Γout∗。很多人设计时忽略了这一点，很可惜。软件（如ADS）可以帮你求GaG_aGa，但有些软件可能不会直接给出。这时候你必须自己把ΓoutΓ_{out}Γout算出来，因为这是做输出匹配（output matching）的依据。你最终一定要算出它。
GaG_aGa是单变量函数 ：仔细看GaG_aGa的公式。里面变量似乎有 ΓsΓ_sΓs和ΓoutΓ_{out}Γout？但注意，ΓoutΓ_{out}Γout本身又是 ΓsΓ_sΓs的函数。所以，当后级强制匹配（ΓL=Γout∗Γ_L = Γ_{out}^*ΓL=Γout∗）后，GaG_aGa最终只是ΓsΓ_sΓs的单一函数 。你每给定一个ΓsΓ_sΓs(设计好一个输入匹配网络)，就对应一个GaG_aGa值。
设计流程 ：你先给一个ΓsΓ_sΓs（比如为了低噪声），就能算出一个GaG_aGa。然后，你必须用公式把对应的ΓoutΓ_{out}Γout算出来，这样才完成了输出匹配网络的设计。不能只顾着输入，忘了输出。

为了画图方便，我们定义一个归一化增益 gag_aga：将GaG_aGa除以 ∣S21∣2|S21|²∣S21∣2。这样，gag_aga的范围就在0到 Gmax/∣S21∣2G_{max}/|S21|²Gmax/∣S21∣2 之间。

一个重要原则：
选择ΓsΓ_sΓs时必须避开"输入稳定圆"（Input Stability Circle）

为什么？因为ΓoutΓ_{out}Γout是ΓsΓ_sΓs的函数。如果你选择的 ΓsΓ_sΓs恰好使得 |ΓoutΓ_{out}Γout| = 1，那就糟了------这正是输入稳定圆 的定义。在史密斯圆图上，如果你的ΓsΓ_sΓs 选在这个圆上（或圆内不稳定区域），会发生什么？

此时 |ΓoutΓ_{out}Γout| = 1。由于后级是共轭匹配（ΓLΓ_LΓL = Γout∗Γ_{out}^*Γout∗），那么 |ΓLΓ_LΓL| = 1，且 ΓinΓ_{in}Γin 和ΓsΓ_sΓs也满足某种关系，最终会推导出 |ΓinΓ_{in}Γin*ΓsΓ_sΓs| = 1 的条件。这正是一个完美的振荡器条件！

从GaG_aGa公式也能看出：当 |ΓoutΓ_{out}Γout| → 1 时，分母 (1 - |ΓoutΓ_{out}Γout|²) → 0，导致 GaG_aGa → 无穷大 。增益无穷大，就是振荡了。

所以，选择ΓsΓ_sΓs时必须远离输入稳定圆 。最稳妥的方法就是先让晶体管在整个频段无条件稳定（K>1），否则这个区域太危险。

根据上述理论，现在来画GaG_aGa这个圆

对于给定的一个归一化增益值 gag_aga（对应一个GaG_aGa值），在史密斯圆图（ΓsΓ_sΓs 平面）上，满足该增益的所有ΓsΓ_sΓs 的轨迹，是一个圆 。

这个圆的方程是：|ΓsΓ_sΓs - CaC_aCa| = RaR_aRa。其中 CaC_aCa是圆心，RaR_aRa是半径。

推导过程我们不细究，但有一个非常有趣且课本很少提到的结论：
这个等增益圆的圆心 CaC_aCa，其角度（相位）与输入稳定圆的圆心的角度是完全相同的！

这意味着，从原点（史密斯圆图中心）画一条通过CaC_aCa的射线，这条线也一定会通过输入稳定圆的圆心。换句话说，所有等增益圆的圆心，都落在"输入稳定圆圆心"与"史密斯圆图中心"的连线上 。

这个发现有什么用？

它给了我们一个强大的直觉：你可以简单地画出这条连线，就能预判等增益圆和输入稳定圆的大致分布关系。
圆上有无数点，选哪个？

等增益圆上的每一个点（即每一个 ΓsΓ_sΓs），都能让你得到相同的可用功率增益GaG_aGa 。现在问题来了，给你一个圆，比如图上有A和B两点，你会选哪一点作为你的 ΓsΓ_sΓs设计值？

这需要你为老板和公司着想，考虑产品的可生产性 和鲁棒性。

A点：更靠近史密斯圆图中心（接近50欧姆）。
- 优点：输入阻抗接近50欧姆，匹配网络更容易实现，对元件参数的偏差（容差）不敏感（Robust）。也就是说，即使电感电容值有些许误差，性能变化不大。
- 缺点：可能不是最佳噪声点（对LNA而言），并且匹配网络的Q值可能较高，导致插入损耗增加，对功率放大器（PA）设计不利。
B点：更靠近输入稳定圆（即更靠近不稳定区域）。
- 缺点：非常敏感！元件参数只要有微小偏差，就会引起输入反射系数（Γs）、电压驻波比（VSWR）和增益的剧烈变化。生产时良率会很低。
- 优点：可能更接近你想要的其它性能（如噪声），但稳定性风险极高。

结论：

利用"等增益圆圆心与输入稳定圆圆心共线"这个规律，你可以迅速判断：一定要选择连线内侧（靠近圆图中心一侧）的点（如A点） ，而远离外侧（靠近稳定圆）的点（如B点）。这样设计出的电路稳定性好，对生产公差容忍度高，这才是工程师真正该考虑的重点。

学了这么久，如果做出来的产品不能稳定生产，那就白学了。请记住这个概念。

情况一：K > 1（无条件稳定）

好的，接下来我们讨论恒定可用功率增益圆 在两种情况下的表现：K > 1 和 K < 1。画出来的圆会非常不同。当然，我还是建议大家在 K > 1 的条件下设计。

首先，我们把晶体管设置成无条件稳定（K>1，|Δ|<1）,然后我们来画恒定可用增益圆（GaCircleG_a CircleGaCircle ）。

怎么画这个圆？

通常软件有两种画法：

指定增益值法：你直接指定要画增益为多少 dB（比如 10dB，15dB）的圆。如果增益值超出了可能范围，软件就不画。
从 GmaxG_{max}Gmax 向下递减法 ：这种方法更好用。因为 K>1 时存在一个最大可用增益 GmaxG_{max}Gmax 。这个GmaxG_{max}Gmax 在史密斯圆图上对应的是一个点 ，而不是一个圆。这个点就是 ΓmsΓ_{ms}Γms （源端共轭匹配点）。
所以，用图解法求ΓmsΓ_{ms}Γms的另一种方法，就是画GaG_aGa圆：找到那个半径为零的点，那就是 ΓmsΓ_{ms}Γms。 图解法在匹配设计时很直观，很容易在圆图上完成设计。

从 GmaxG_{max}Gmax 这个点开始，每降低一定增益（比如 1dB），就画一个等增益圆。你可以根据自己的需要画几个。这样就能直观地看到，随着增益降低，可供选择的 ΓsΓ_{s}Γs范围（圆的大小）在变大。

所有等增益圆的圆心，都落在 ΓmsΓ_{ms}Γms点与输入稳定圆（Input Stability Circle）圆心的连线上。前面已经解释过，这是因为圆心角度公式相同决定的。

设计选择与生产良率

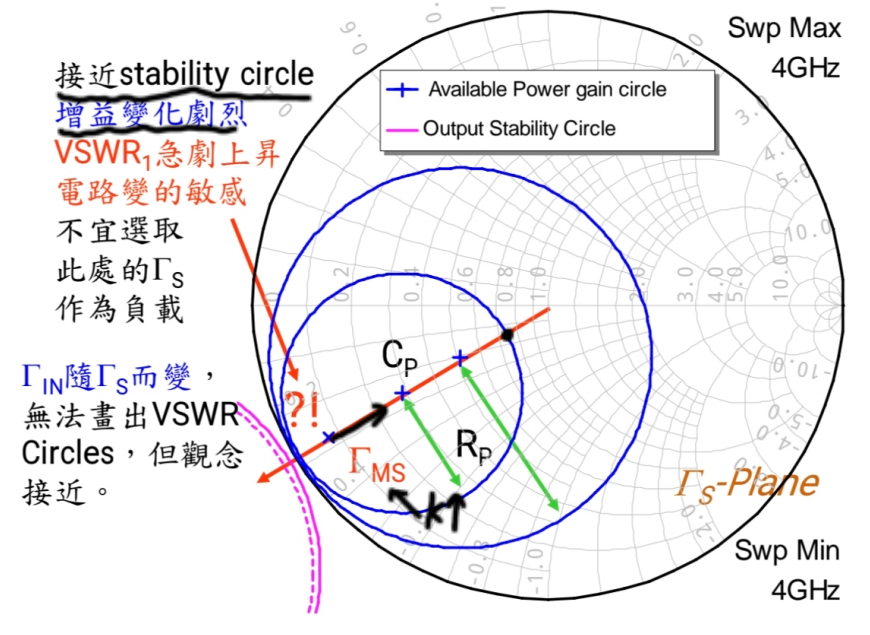
现在看图，K>1 时，输入稳定圆（红色虚线）在史密斯圆图单位圆之外，整个圆图都是稳定区域。

假设我们的设计目标是最大增益 Gmax，对应的点就是ΓmsΓ_{ms}Γms。

现在考虑生产中的元件误差：如果我们设计的匹配网络因为误差，导致实际的 ΓsΓ_{s}Γs偏离了目标点ΓmsΓ_{ms}Γms，会发生什么？

如果向内偏离（朝向圆图中心） ：恭喜你！你进入了一片"青青草原"。这里的等增益线（圆圈）很稀疏，意味着增益变化平缓。即使ΓsΓ_{s}Γs偏了一点，增益下降也不多，电路性能稳定。良率高！
如果向外偏离（朝向稳定圆） ：糟糕！你走向了"悬崖峭壁"。越靠近输入稳定圆，等增益线越密集。这意味着ΓsΓ_{s}Γs的微小偏差就会导致增益急剧下降（甚至可能滑向不稳定区）。良率极低！

于是，我们可以在这里提出一个问题，K 刚好等于 1 到底好不好？

答案是绝对不好！

想象一下，如果 K 刚好等于 1，那么ΓmsΓ_{ms}Γms这个点会落在哪里？它会正好压在输入稳定圆的边界上 ！这时，你的设计点就坐在了"悬崖边"。任何微小的元件误差，都极易将电路推入不稳定区（K<1）或者导致增益暴跌。电路会变得极其敏感，生产几乎无法控制。

因此，我们绝不能 让 K 刚好等于 1。通常会将 K 值设计在 1.05 到 1.1 左右。这样，ΓmsΓ_{ms}Γms点会从"悬崖边"向圆图中心方向移动一些。虽然牺牲了一点理论最大增益（可能零点几到 1dB），但换取的是宽松得多的等增益线 和对误差的强健性（Robustness） 。

从系统角度看，匹配网络本身的损耗也会影响最终增益，所以牺牲一点点理论增益换取高良率和稳定性能，整体效果往往更好。

情况二：K < 1（潜在不稳定）

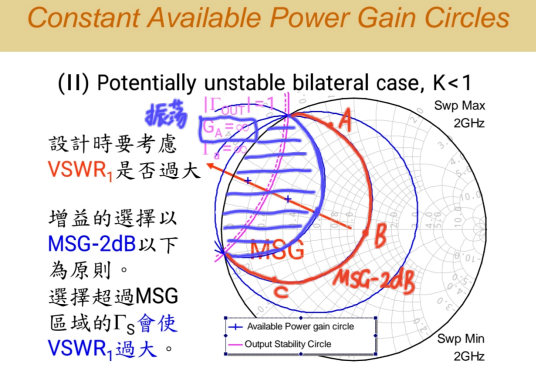
1.当 K < 1 时，输入稳定圆的一部分侵入了史密斯圆图单位圆内部。

这时画出的等增益圆系列会有一个可怕的特征：那个半径为零的"点"（对应理论上的最大增益）并不在圆图内稳定的ΓsΓ_{s}Γs区域，而是落在了输入稳定圆的圆周上。

这意味着什么？

如果你想获得接近理论最大的增益 ，就必须选择非常靠近输入稳定圆的ΓsΓ_{s}Γs点。
这些点极度危险：不仅电路性能（增益、输入驻波比 VSWR）对误差超级敏感，而且很容易因为微小偏差就落入不稳定区，直接振荡。
此时的所谓"最大增益"在理论上是无限大（振荡），但实际设计中你必须主动远离这些点，牺牲大量增益来确保稳定性。这也是为什么 MSG（最大稳定增益）成为一个重要参考指标，它告诉你一个增益上限，但实际设计值必须远低于它（例如 MSG - 2dB 或更多）。

2.并且，我们不难从图中观察到，当 K < 1 时，画出来的等增益圆都有一个共同特点：它们都会通过两个固定的点 。可以证明，这两个点同时也是输入稳定圆（粉红色）与史密斯圆图单位圆的交点 。
这代表什么物理意义？

之前讲过，输入稳定圆（ΓinΓ_{in}Γin=1的轨迹）意味着振荡条件。在这两个交点上，ΓoutΓ_{out}Γout 也等于 1，且互为共轭，满足 |ΓinΓ_{in}Γin * ΓoutΓ_{out}Γout| = 1 的振荡条件。因此，如果你的ΓsΓ_{s}Γs 选在这两点上，增益 Ga 将是无限大 （振荡）。

同时，这也意味着输入反射系数 ΓinΓ_{in}Γin也趋于无穷大，导致输入电压驻波比VSWR 也会变得非常大，远超通常要求的 2.0。

3.同样，这些等增益圆的圆心也落在输入稳定圆圆心与史密斯圆图中心的连线上。

我们设计时必须考虑输入 VSWR < 2.0 的要求。越靠近粉红色的稳定圆，增益可能越高，但 VSWR 绝对超标。

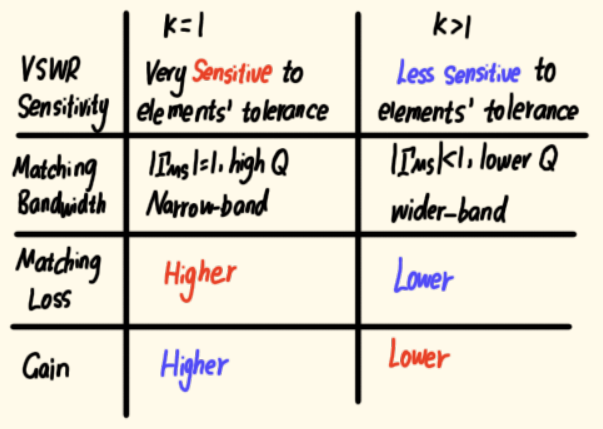
软件（如ADS）在 K<1 时画等增益圆，通常不会从无限大增益开始画 。它画出的第一个等增益圆，通常对应 MSG（最大稳定增益） 。这暗示了：你绝对不应该选择增益超过 MSG 的区域，那是危险区！

很多教材会建议选择在 MSG - 2 dB 的等增益圆上进行设计。

假设我们选定了一个 MSG - 2 dB 的圆（如图示蓝色圆）。圆上有 A、B、C 等多个点，都能得到相同的增益 。但是，它们的输入 VSWR 会一样吗？
答案是完全不同！

VSWR 由ΓinΓ_{in}Γin决定，而ΓinΓ_{in}Γin又是由 ΓsΓ_{s}Γs和 S 参数共同决定的。当你沿着这个圆移动ΓsΓ_{s}Γs时，ΓinΓ_{in}Γin会剧烈变化。

越靠近输入稳定圆 （如图中靠近粉红圆的部分），ΓinΓ_{in}Γin的模值越大，输入 VSWR 越差（趋于无穷大）。
越远离输入稳定圆 （如图中靠近圆图中心的部分），ΓinΓ_{in}Γin的模值越小，输入 VSWR 越好接近1。

综合结论

K = 1 是最差的选择：设计点位于稳定边界，电路极其敏感，良率无法保证。
K > 1（建议 1.05-1.2）是稳健的设计选择：牺牲少量理论增益，换来电路对元件误差的不敏感性和高生产良率。Γms 点位于圆图内部安全区域。
K < 1 应极力避免用于放大器设计：必须采取稳定措施（如加电阻、反馈）将 K 值提升到大于 1，或者被迫工作在大大降低的增益下，设计复杂且风险高。
利用等增益圆辅助设计：通过观察等增益圆的疏密，可以直观判断设计点的稳健性。要选择等增益线稀疏、远离稳定边界的区域。
考虑系统总损耗：软件计算的 Ga 不包含匹配网络的实际损耗。一个高增益但难实现、损耗大的设计，其最终性能可能不如一个增益略低但易实现、损耗小的稳健设计。

如何选择最佳设计点？

这就是课本不会教，而需要工程师经验判断的地方：

性能（增益与VSWR的权衡） ：同样是 MSG - 2 dB 的增益，选择 C点（远离稳定圆）会获得更好的输入 VSWR，但可能离你想要的其它性能（如最佳噪声点）较远。选择 A 点或 B 点 VSWR 会变差。
电路的鲁棒性与生产良率：和之前 K>1 的分析一样，C点附近区域等增益线更稀疏，匹配网络对元件误差（容差）不敏感，生产良率高。而靠近稳定圆的A、B点区域，电路性能对误差极其敏感，属于"悬崖"地带。
匹配网络实现难度：C点更靠近史密斯圆图中心（50欧姆），通常意味着匹配网络更容易设计，可能Q值更低，带宽更宽，插入损耗更小。

我的最终建议：

尽量避免在 K < 1 的不稳定区域直接设计放大器，这绝非好事。最佳实践是：首先通过稳定措施（如加电阻、反馈），让晶体管在目标频段满足 K > 1（且略大于1，如1.05）。然后使用 K>1 的等增益圆进行稳健设计。

在 K>1 的圆图上，选择等增益圆上远离稳定边界、靠近圆图中心的点（即使这意味着牺牲零点几到1 dB的增益），这样设计的电路性能稳定、生产良率高，综合系统性能（算上匹配网络损耗后）往往更优。

恒定工作功率增益圆GPG_PGP

接下来我们看用于功率放大器（PA）设计 的恒定工作功率增益圆。它的思路和可用增益圆是对偶的。

功率放大器追求最大输出功率，这由最佳负载线决定。因此，输出负载 ΓLΓ_LΓL 通常被固定在一个特定的"最佳负载"ΓoptΓ_{opt}Γopt 上，以获得最大功率输出和效率。此时，输出端不一定是共轭匹配 （因为共轭匹配对应最大增益，而非最大功率）。

既然输出负载已为功率优化固定，那么输入端就负责提供足够的增益 。因此，输入端进行共轭匹配（Γs=Γin∗Γ_s = Γ_{in}^*Γs=Γin∗），以使从输入端到负载的功率传输增益最大化。

数学关系

工作功率增益 GpG_pGp 的公式中，当强制输入端共轭匹配（Γs=Γin∗Γ_s = Γ_{in}^*Γs=Γin∗）后，GpG_pGp 最终只是 ΓLΓ_LΓL的单一函数 。因此，我们可以在 ΓLΓ_LΓL平面 上画出等 GpG_pGp 圆。

同样的，和GAG_AGA圆类似，我们需要谨慎选择输出匹配电路，避免选择的 ΓLΓ_LΓL，使得 ΓinΓ_{in}Γin = 1 （即输出稳定圆）。如果ΓLΓ_LΓL选在这个圆上，同样会满足振荡条件，GpG_pGp理论上无限大，输出 VSWR 也会极差。
设计要点

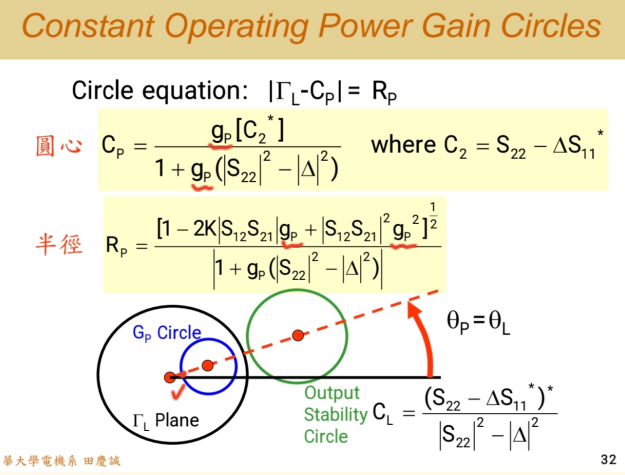
圆心规律 ：同理，等GpG_pGp圆的圆心，与输出稳定圆（Output Stability Circle）的圆心 位于从史密斯圆图中心出发的同一条射线上。
圆上的选择 ：在一个给定的等GpG_pGp圆上，所有ΓLΓ_LΓL点都提供相同的工作功率增益GpG_pGp(即存在不同的输出匹配电路，能够使电路达到同样的功率增益)。但是，它们对应的输出端 VSWR 和电路稳定性（对误差的敏感度）截然不同 。
- 应选择：远离输出稳定圆、更靠近史密斯圆图中心的点。这样的选择能保证更好的输出匹配（VSWR更低）、更宽的带宽、对元件误差更不敏感（高良率）。
- 应避免：靠近输出稳定圆的点，虽然增益相同，但输出匹配差，电路极易因微小误差而性能剧变或不稳定。

所以，工作功率增益GpG_pGp 什么时候达到最大？当输入端已经匹配（Γs=Γin∗Γ_s = Γ_{in}^*Γs=Γin∗）时，如果输出端也实现共轭匹配 （ΓL=ΓmlΓ_L = Γ_{ml}ΓL=Γml），那么这时候的增益就是最大可用增益GmaxG_{max}Gmax 。也就是说，GP,maxG_{P,max}GP,max就是GmaxG_{max}Gmax。当然，这只有在 K > 1 时才成立。

刚才讲可用功率增益 GaG_aGa的部分时，我们似乎忘记提它的最大值证明。其逻辑是一样的：GaG_aGa的最大值也出现在其增益圆的半径等于 0 的时候。注意，GaG_aGa的公式和GpG_pGp不同。

通常，我们所说的 最大增益（MAG, Maximum Available Gain） ，指的是 K>1 时的 Gmax。很少有人特意区分是"最大可用增益"还是"最大工作增益"，习惯上都用 MAG 来表示。

图解法的应用

之前提到，如何用图解法找到ΓmsΓ_{ms}Γms？答案是：画 GaG_aGa圆 ，其最大增益点（半径为零的点）就是ΓmsΓ_{ms}Γms 。

同理，如何用图解法找到ΓmlΓ_{ml}Γml？答案是：画 GpG_pGp圆 ，其最大增益点（半径为零的点）就是ΓmlΓ_{ml}Γml 。

这两个过程是独立的：通过GaG_aGa圆找ΓmsΓ_{ms}Γms，通过GpG_pGp圆找ΓmlΓ_{ml}Γml。但它们在最大值点上是关联的：这两个点分别实现前后级共轭匹配，共同达到同一个理论最大增益 GmaxG_{max}Gmax。

除了用软件直接列表求解ΓmsΓ_{ms}Γms和ΓmlΓ_{ml}Γml，你完全可以用这种图解法找到它们，然后直接设计匹配网络。

找到ΓmlΓ_{ml}Γml后，你就要设计一个匹配网络，将 50 欧姆负载匹配到ΓmlΓ_{ml}Γml。请问，匹配的方向是从 50 欧姆走向ΓmlΓ_{ml}Γml，还是从ΓmlΓ_{ml}Γml走向 50 欧姆？

这个问题极其重要，80% 学习微波工程的人都会搞错方向，我以前也错过。

你必须根据 ΓmlΓ_{ml}Γml的物理意义 来判断：ΓmlΓ_{ml}Γml是从晶体管输出端向负载方向看 所期望的反射系数。因此，匹配网络应该放在晶体管和50欧姆负载之间。设计的思路是：从负载端（50欧姆）开始，通过匹配网络，"变换"到晶体管输出端所期望的ΓmlΓ_{ml}Γml 。

所以，正确的匹配方向是从 50 欧姆（史密斯圆图中心）出发，设计电路，最终到达ΓmlΓ_{ml}Γml点 。如果你反过来从ΓmlΓ_{ml}Γml开始向50欧姆设计，那就全错了。

我一直在强调：反射系数和匹配都是有方向性的。方向搞错，全盘皆输。一定要结合物理电路来理解。

情况一:K > 1 的情况

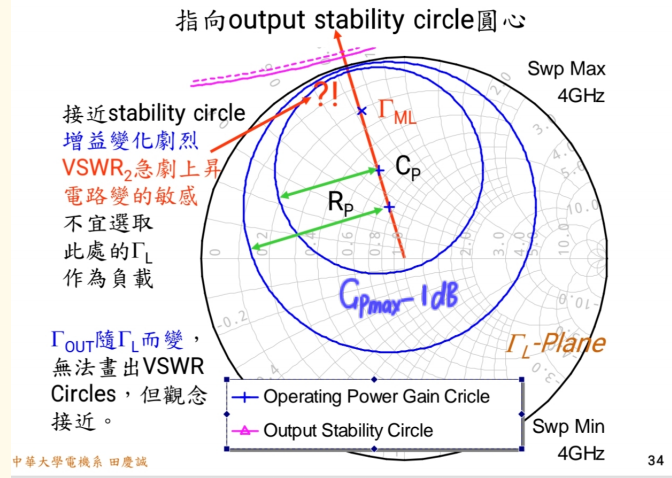
在 K > 1 时，ΓmlΓ_{ml}Γml点会落在史密斯圆图内部（稳定区域）。

K = 1 是危险边界 ：如果 K 刚好等于 1，那么ΓmlΓ_{ml}Γml点会刚好落在输出稳定圆的边界上。选择这一点设计，电路会非常敏感、难以实现，且极不稳定。
稳健设计 ：我们通常不选择理论最大增益点（ΓmlΓ_{ml}Γml）。而是选择比GmaxG_{max}Gmax低 1 dB 的等GpG_{p}Gp圆。在这个圆上，有无穷多个ΓLΓ_{L}ΓL点可供选择，都能提供GmaxG_{max}Gmax - 1 dB 的增益。
- 错误选择：选择靠近输出稳定圆边界的点（如图中某侧）。这里等增益线非常密集，意味着增益和 VSWR 对元件误差极度敏感。性能会剧烈变化，生产良率低。
- 正确选择：选择远离稳定圆、更靠近史密斯圆图中心的点（如图中另一侧）。这里等增益线稀疏，电路对误差不敏感，性能稳定，匹配网络也更容易实现（通常 Q 值更低，带宽更宽）。

情况二:K < 1 的情况

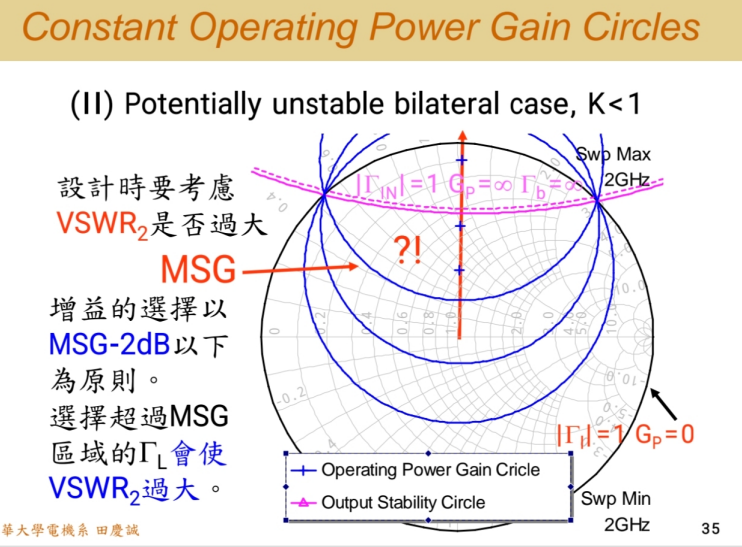
此时画出的GpG_{p}Gp圆系列，第一个圆通常对应 MSG。软件不会给你画出增益超过 MSG 的圆（那是危险的振荡区）。

危险区域 ：当ΓLΓ_{L}ΓL选在输出稳定圆上时，ΓinΓ_{in}Γin = 1，GpG_{p}Gp理论无穷大，输出 VSWR 也趋于无穷。因此，靠近输出稳定圆的区域，增益可能更高，但 VSWR 极差且电路濒临振荡。
设计建议 ：如果必须在 K<1 的区域设计（应尽量避免），课本建议选择 MSG - 2 dB 的等GpG_{p}Gp圆。同样，在这个圆上：
- 应避免：选择靠近输出稳定圆的点（VSWR 差，不稳定）。
- 应选择：选择远离稳定圆、靠近圆图中心的点（虽然增益相同，但输出 VSWR 更好，电路更稳健）。

最佳实践总结

最好的方法仍然是：先通过稳定措施，让晶体管在目标频段满足 K > 1（例如 1.05 到 1.2）。然后在 K>1 的 Gp 圆上，选择一个增益略低于 GmaxG_{max}Gmax、且远离稳定边界的ΓLΓ_{L}ΓL点进行设计。这样牺牲一点理论增益，换来的是电路的稳定性、生产良率和整体性能的可靠性。

不同放大器的通用设计法则

无论设计哪种放大器，前三个步骤都是相同的，如下图所示:

1.确定设计目标/限定范围

2.选择合适的晶体管，计算对应偏压下的S参数，MSG和MAG.

3.将晶体管的K值全部提升至K>1

1. 通用驱动放大器（General Purpose / Driving Amplifier）

这是最简单的情况。

步骤：有了S参数后，首先确保晶体管在目标频段无条件稳定（K > 1） 。然后，软件可以直接解出前后级同时共轭匹配的解（ΓmsΓ_{ms}Γms和 ΓmlΓ_{ml}Γml）。
设计：根据ΓmsΓ_{ms}Γms和ΓmlΓ_{ml}Γml分别设计输入和输出匹配网络。
特点：这种设计追求最大增益，通常噪声性能（NF）不是首要考虑。设计过程可以非常快（理论上15分钟内可完成初步设计）。仿真结果中，增益曲线在目标频率会出现峰值，输入输出驻波比（VSWR）通常也会调得很好。
后续工作：真正的挑战在于将仿真中的理想元件替换为实际元件（考虑寄生参数、封装、可用标称值）并进行优化调试，这个过程可能很漫长。

2. 低噪声放大器（LNA）设计

LNA设计需要权衡增益、噪声和输入匹配。

获取参数 ：首先需要获得晶体管的噪声参数 （最小噪声系数 FminF_{min}Fmin，最佳噪声反射系数ΓoptΓ_{opt}Γopt等）。
权衡过程 ：在史密斯圆图（ΓsΓ_{s}Γs平面）上，你会画出两类圆：
- 等噪声系数圆（Noise Circle） ：越靠近ΓoptΓ_{opt}Γopt点，噪声系数越好。
- 等可用增益圆（Ga Circle） ：越靠近ΓmsΓ_{ms}Γms点，增益越高。
- 通常，ΓoptΓ_{opt}Γopt（最佳噪声点）和ΓmsΓ_{ms}Γms（最大增益点）不重合 。ΓoptΓ_{opt}Γopt 点往往对应较差的输入匹配（高 VSWR）。
设计选择 ：工程师需要在增益（Ga）、噪声系数（NF）和输入 VSWR 三者之间进行权衡。
- 你不能只看噪声最好就选ΓoptΓ_{opt}Γopt，因为那可能导致输入 VSWR > 2.0，不满足系统要求。
- 最终的ΓsΓ_{s}Γs可能选在ΓoptΓ_{opt}Γopt和ΓmsΓ_{ms}Γms之间的某个折中点，以确保噪声可接受、增益足够，同时输入 VSWR 达标（例如 < 2.0）。
完整验证流程 ：
1. 选定一个折中的ΓsΓ_{s}Γs。
2. 由ΓsΓ_{s}Γs计算出ΓoutΓ_{out}Γout。
3. 设定输出匹配：ΓLΓ_{L}ΓL = Γout∗Γ_{out}^*Γout∗（共轭匹配以获取增益）。
4. 由ΓLΓ_{L}ΓL反算出此时的ΓinΓ_{in}Γin。
5. 用ΓsΓ_{s}Γs和ΓinΓ_{in}Γin计算输入 VSWR。如果 VSWR 不达标，回到第1步，重新选择ΓsΓ_{s}Γs。
6. 同时验证ΓLΓ_{L}ΓL是否远离输出稳定圆，确保稳定性。

3. 功率放大器（PA）设计

PA设计追求最大输出功率和效率，其思路与LNA不同。

负载牵引（Load Pull） ：PA的核心是找到能产生最大输出功率（或最佳效率）的最佳负载阻抗 Γopt（或一个范围）。这个点通常通过负载牵引测试或大信号模型获得。
权衡：在史密斯圆图（ΓLΓ_{L}ΓL平面）上，你会看到：
- 等功率输出圆（Power Contour）：形状像"眼睛"，中心是最大功率点。
- 等工作增益圆（Gp Circle） ：中心是最大增益点ΓmlΓ_{ml}Γml。
- 通常，最大功率点ΓoptΓ_{opt}Γopt 和最大增益点 ΓmlΓ_{ml}Γml也不重合 。ΓoptΓ_{opt}Γopt往往位于低阻抗区（实部较小，带感性）。
设计选择 ：对于PA，通常优先选择最大功率点ΓoptΓ_{opt}Γopt，牺牲一些增益来换取功率和效率。只要增益不至于太低而影响整体效率，这个权衡是可接受的。
一个关键点：输出 VSWR ：
- 选择ΓoptΓ_{opt}Γopt通常会导致很差的输出匹配（输出 VSWR 很高，例如 > 4.0）。
- 但是，对于许多PA应用，输出 VSWR 并不严格限制 。为什么？
  考虑信号流：PA输出端一般接的是天线。如果天线是完美匹配的（50欧姆），那么从PA输出端看出去的反射系数 ΓL（天线端）为0。这时，无论PA自身的S22S_{22}S22多差，因为没有反射波从天线回来，所以S22S_{22}S22根本不会影响前向传输的功率。也就是说，在负载（天线）完美匹配的情况下，PA的输出匹配好坏不影响输出功率。
- 例外情况 ：如果天线失配（如被拔掉、损坏或被遮挡），会产生强反射波回到PA，此时PA差的输出匹配S22S_{22}S22会导致问题，可能引起振荡、烧毁或频谱再生。因此，一些系统会要求PA在负载失配时仍能稳定工作（负载失配容限）。

一个实际案例 ：

有位学长在明基遇到一个案例：PA输出功率3W达标，但接上良好天线后，整机辐射杂散（Spurious Emission）超标。他们的"解决方案"是在天线前故意制造一个大的失配（将天线端VSWR调到4.0），让部分功率反射回来以降低辐射功率。但这导致了新的问题：反射回来的信号影响了PA的工作状态（如引起调制失真）。

最终的责任落在了PA设计者（那位学长）身上。他的解决方法是：在调整输出匹配网络时，不仅匹配到功率点，还精细调整了输出网络的相位，使得即使在负载失配（VSWR=4.0）的特定相位下，也能将反射回来的信号"引导"到一个不影响PA核心性能的状态。这需要非常深入的理解和调试能力。

PA设计流程简述：

确定最佳功率负载点ΓoptΓ_{opt}Γopt（通过负载牵引或模型）。
设定 ΓLΓ_{L}ΓL= ΓoptΓ_{opt}Γopt（或在其附近权衡）。
由 ΓLΓ_{L}ΓL计算出此时的 ΓinΓ_{in}Γin。
设计输入匹配：ΓsΓ_{s}Γs = Γin∗Γ_{in}^*Γin∗（共轭匹配以获取增益）。
验证ΓsΓ_{s}Γs是否远离输入稳定圆，确保稳定性。
（可选）计算输出 VSWR，但通常不作为硬性约束，除非系统有特殊要求（如负载失配容限）。