相似矩阵是线性代数中描述矩阵 "等价变换" 的核心概念,核心作用是通过可逆矩阵转化,简化矩阵运算(如幂运算、行列式计算)和结构分析(如对角化),与特征值、特征向量紧密关联。
一、相似矩阵的严格定义
1. 前提条件
仅针对 n 阶方阵 讨论(非方阵无相似关系),涉及的转化矩阵为 可逆 n 阶方阵 (记为P,满足 存在)。
2. 数学定义
设A、B为 n 阶方阵,若存在 可逆矩阵P ,使得: 则称矩阵A与B 相似 ,记为A∼B;可逆矩阵P称为 相似变换矩阵。
3. 核心本质
相似矩阵是 "同一线性变换在不同基下的矩阵表示"------ 矩阵A和B描述的是同一个线性变换,只是选取的向量空间基不同,通过相似变换矩阵P实现基的转换。
二、相似矩阵的核心性质(含推导逻辑)
相似矩阵的核心特征是 "结构等价,关键属性不变",以下性质按 "等价关系→数值属性→运算属性" 分类,均附严谨推导:
1. 相似关系是等价关系(满足 3 条性质)

2. 数值属性不变(核心不变量)
- 性质 1:行列式相等 :若A∼B,则∣A∣=∣B∣
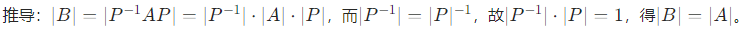
- 性质 2:秩相等:若A∼B,则r(A)=r(B)

- 性质 3:迹相等 :若A∼B,则tr(A)=tr(B)
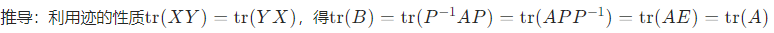
- 性质 4:特征多项式、特征值相同 :若A∼B,则∣A−λE∣=∣B−λE∣,且A与B的特征值完全相同(重数一致)
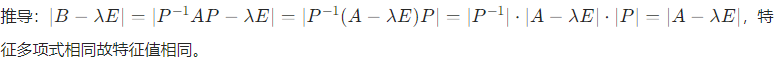
3. 运算属性不变(运算后仍相似)
设A∼B,P为相似变换矩阵,k为常数,m为正整数,f(x)=amxm+⋯+a1x+a0为多项式,则:

三、重要推论(核心应用基础)
