论文基本信息 (Basic Information)
| 标题 (Title) | Analog optical computer for AI inference and combinatorial optimization |
|---|---|
| Adress | https://doi.org/10.1038/s41586-025-09430-z |
| Journal/Time | Nature (24年11月的文章,25年7月accept,25年9月pub) |
| Author | 微软研究院(含Barclays(巴克莱银行) 和 剑桥大学) |
1. 核心思想 (Core Idea)
- 通用的、混合架构的模拟光子计算机(AOC)可以做 AI 推理(AI Inference)和 组合优化问题(Combinatorial Optimization)。
- 不动点搜索(Fixed-point Search):Continuous Analog Loop:信号在每一轮迭代中都不变成数字信号,一直在模拟域里跑。只有在最后算完了,才进行一次读出。这极大地提升了效率和速度。Unifying Abstraction:让输入在网络里循环,直到输出稳定。类似于优化问题找到最低点不再动了。这种特性也能最终抵抗模拟噪声。
2. 研究背景与动机 (Background and Motivation)
现在的数字计算(CPU/GPU)面临能耗和速度的物理瓶颈。
光计算快且省电,但目前存在的问题有:
- 频繁的数模转换(AD/DA 转换): 以前的混合系统,光算完一步就要转成数字信号存起来,处理完再转回光。这导致很高的能耗和时间都浪费在转换上,而不是计算上。
- 专用性太强: 做 AI 的光芯片做不了优化,做优化的做不了通用 AI。
- 模拟噪声: 模拟计算存在噪声,导致精度很难做高。
3. 方法论 (Methodology)
- 输入(Input):
通过 MicroLED 阵列发出的光强度来表示。在 AI 任务中,输入是图像或数据(比如手写数字)。在优化任务中,输入是问题的参数(比如金融交易的约束条件、MRI 图像的测量数据)。
权重/系数: 通过空间光调制器(SLM)的像素透光率来表示。这对应神经网络的权重矩阵 W W W 或优化问题的系数矩阵 - 输出(Output): 系统最终收敛到的"稳定状态"(Fixed Point)。这对应着 AI 的预测结果(分类标签、回归曲线)或优化的最佳解(比如最优的交易结算方案)。
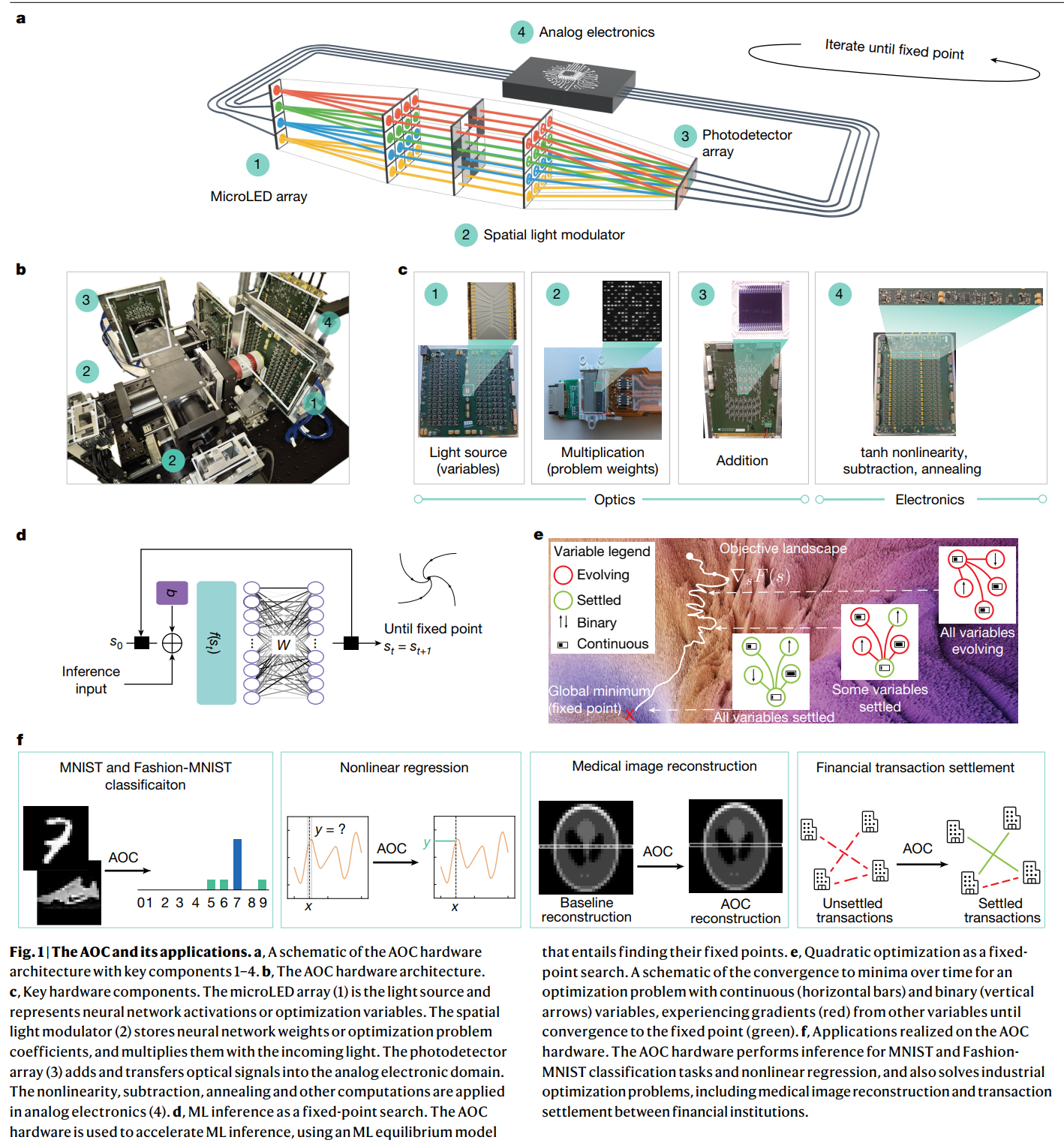
MicroLED(光源/变量)发出光,穿过 SLM,最后打在光电探测器上。这完成了矩阵乘法的操作。然后信号进入旁边的模拟电路,处理完后再控制 MicroLED 发光,形成闭环 。
图 1a & 1c:左边是 MicroLED 阵列(发光,代表变量 s t s_t st),中间是 SLM(存权重矩阵 W W W),光穿过去就是做乘法。右边是 光电探测器(把光变回电流)。然后信号进入下方的 模拟电路板(图 1c 中的 4 号),在这里加上非线性函数 f ( ⋅ ) f(\cdot) f(⋅),再喂回 MicroLED。 Equation (1): s t + 1 = α ( t ) s t + β W f ( s t ) + γ ( s t − s t − 1 ) + b s_{t+1} = \alpha(t)s_t + \beta W f(s_t) + \gamma(s_t - s_{t-1}) + b st+1=α(t)st+βWf(st)+γ(st−st−1)+b
W f ( s t ) W f(s_t) Wf(st): 矩阵乘法需要算力多,光学部分做,因为光传播就是并行的,速度极快且不发热 。光计算算很快,但存不行。
f ( s t ) f(s_t) f(st) 和其他项: 非线性激活、退火、动量,模拟电子电路做。
公式里的每一项,都在硬件上有对应的物理器件。
1d (AI): 输入 x x x,系统自动演化,最终停在 s ∗ s^* s∗,这就是分类结果。1e (优化):最终停在底部的全局最小值 。
利用了第三维度进行光线扇入扇出,比平面光子芯片更容易扩展矩阵大小。
闭环反馈系统。信号在光和电之间不断循环:
- 光路(Optics): 负责最耗算力的矩阵-向量乘法(MVM)。光穿过 SLM,瞬间完成大规模并行计算。
- 模拟电路(Analog Electronics): 负责非线性操作(如 tanh 函数)、加减法、以及引入"退火"和"动量"等算法所需的动态调节。
- 循环(Iteration): 信号不经过数字转换,直接在光和电之间循环几百上千次,直到系统状态不再变化(达到不动点),才进行读出。
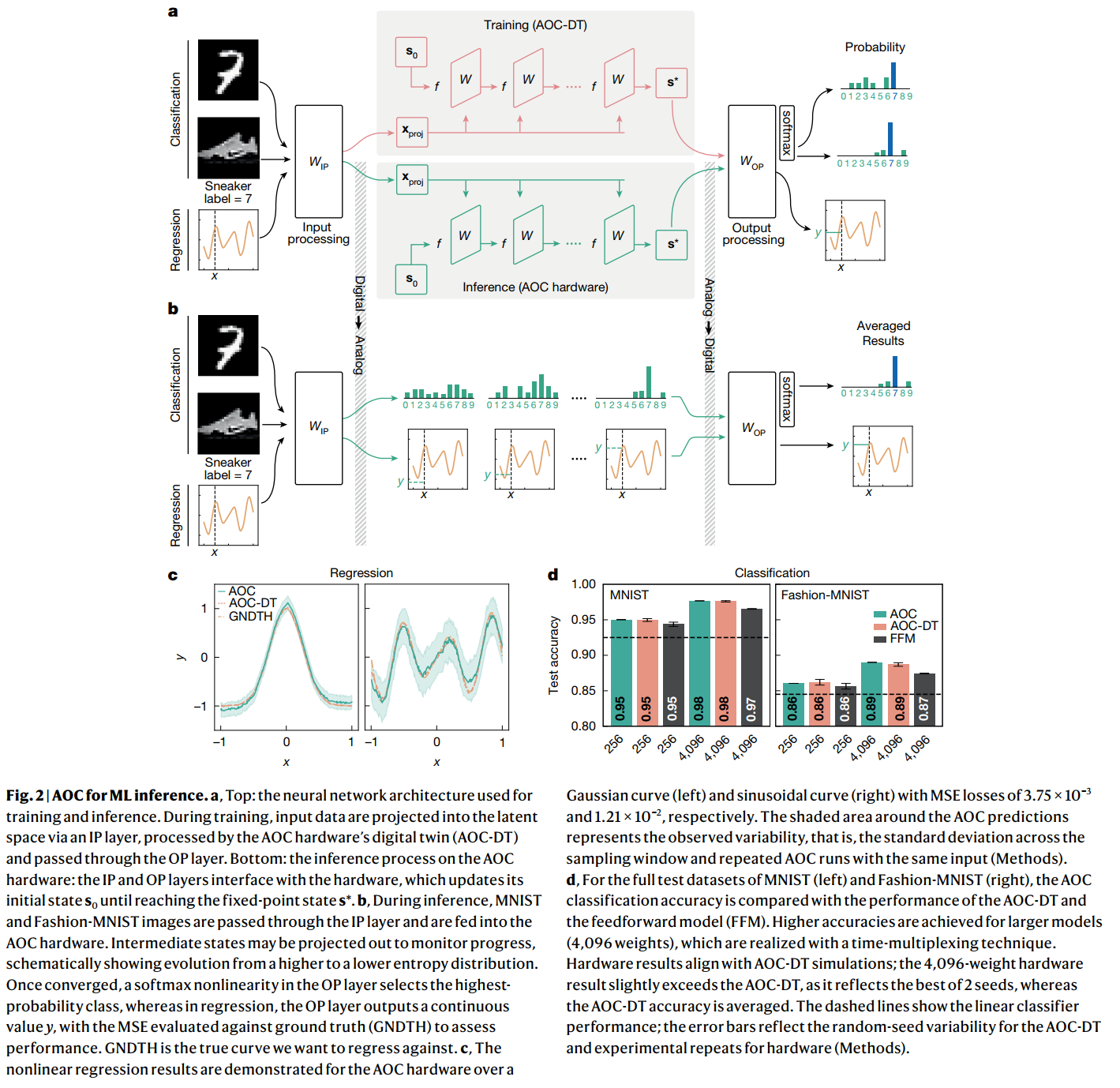
图 2a/b: 展示了怎么做 AI。 MNIST(手写数字)和 Fashion-MNIST(衣物分类)。输入经过一次数字投影(Input Projection),扔进 AOC 循环,出来后再投影一次。可以看到,随着迭代进行,系统输出的概率分布逐渐清晰,最终锁定正确的标签 。
图 2c(非线性回归): 在模拟硬件上拟合了高斯曲线和正弦曲线。那个阴影区域代表了模拟噪声的范围,但平均值(实线)做了正弦波拟合。这证明了光计算机不仅能做简单的分类(如 MNIST),还能做非线性回归,它要求连续数值的高精度输出。
非相干光的使用: 使用的是 MicroLED(非相干光),而不是激光(相干光)。相干光对环境极其敏感(震动、温度都会干扰),而非相干光更鲁棒,更适合大规模制造和集成 。
数字孪生: 在硬件基础上还写了一个与其物理特性高度一致的"可微分数字孪生AOC-DT" 。在电脑上训练模型,把物理缺陷(如噪声)考虑进去,训练好的权重直接部署到光学芯片上就能用,不需要在芯片上重新训练,这大大降低了部署成本 。
全模拟反馈: 在多次迭代直至收敛的过程中,信号从未变成数字信号 。只有在最后读出结果时才做一次转换。这是能效提升的关键。
4. 实验结果 (Experimental Results)
通过图像分类、回归、MRI 重建、金融结算四个案例证明 。
通用性。同一个物理装置,仅仅通过改变输入的系数矩阵和电子增益设置,可以完成分类任务也可以完成优化任务。
在电脑上用数字孪生(AOC-DT)训练。把权重 W W W 量化并写入 SLM,光机直接跑出结果,即使有模拟噪声,因为系统在找"不动点"(吸引子),它会自动修正偏差,抗噪能力很强 。
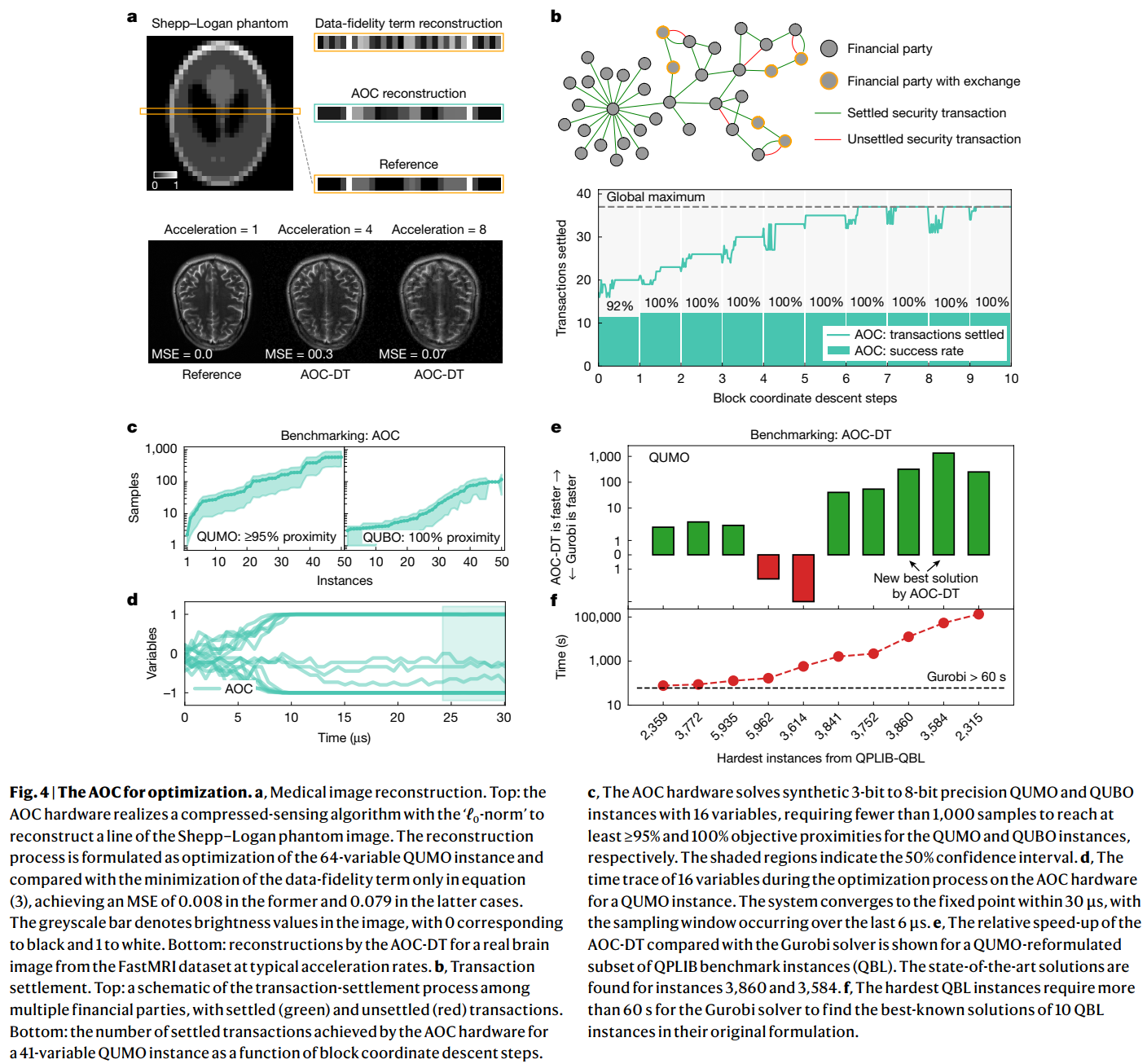
医学MRI用了压缩感知(Compressed Sensing, CS)。虽然图像有百万像素,但如果变换到某个域,大部分系数都是 0(稀疏)。只要能找到那些少数的"非零值",就能用很少的扫描数据还原出完整的图像。 数学公式的理想解决是 L 0 L_0 L0 范数,找到一个图像 x x x,它既能匹配扫描数据 y y y,同时它的非零像素个数( L 0 L_0 L0 范数)最少。传统电子计算去优化 L 1 L_1 L1 范数(像素绝对值之和)。这是一个凸优化问题。
将该问题表达为了二次无约束混合优化(QUMO)。
论文中的 公式 (3) : m i n x , σ 1 2 ∣ ∣ y − A x ∣ ∣ 2 2 + λ 1 1 T σ + λ 2 ( 1 − σ ) T x min_{x, \sigma} \frac{1}{2}||y-Ax||{2}^{2} + \lambda{1}1^{T}\sigma + \lambda_{2}(1-\sigma)^{T}x minx,σ21∣∣y−Ax∣∣22+λ11Tσ+λ2(1−σ)Tx
y y y:扫描到的原始数据(不完整的 k 空间数据)。
A A A:物理过程矩阵(包含了傅里叶变换、小波变换和采样掩码)。
x x x(连续变量): 我们要还原的图像(在小波域的系数),取值范围 [ 0 , 1 ] [0, 1] [0,1] 。
σ \sigma σ: σ ∈ { 0 , 1 } \sigma \in \{0,1\} σ∈{0,1}。
数据保真项 1 2 ∣ ∣ y − A x ∣ ∣ 2 2 \frac{1}{2}||y-Ax||_{2}^{2} 21∣∣y−Ax∣∣22: 这一项要求还原的图像 x x x 必须尽可能符合扫描到的数据 y y y。这在数学上展开是一个二次项( x T A T A x x^T A^T A x xTATAx),正好对应 AOC 硬件中的矩阵乘法部分。
稀疏惩罚项 λ 1 1 T σ \lambda_{1}1^{T}\sigma λ11Tσ: 每当 σ i = 1 \sigma_i=1 σi=1(决定保留一个像素),就得支付 λ 1 \lambda_1 λ1 的代价。为了让总代价最小,系统会倾向于让尽可能多的 σ \sigma σ 变成 0。这就是在模仿 L 0 L_0 L0 范数。
耦合项 λ 2 ( 1 − σ ) T x \lambda_{2}(1-\sigma)^{T}x λ2(1−σ)Tx: 它连接了 x x x 和 σ \sigma σ。展开来看,包含项 σ i x i \sigma_i x_i σixi。这是二进制变量与连续变量的乘积,正是 AOC 擅长的"混合优化(Mixed Optimization)"。如果 σ i = 0 \sigma_i = 0 σi=0(开关关掉): 惩罚变成了 λ 2 x i \lambda_2 x_i λ2xi。为了最小化这一项,系统会强迫 x i x_i xi 趋向于 0。
通过引入二进制变量 σ \sigma σ,将一个极其复杂的组合优化问题,变成了一个 AOC 可以直接求解能量最小值的物理过程。
真实的 MRI 图像有几十万个像素(变量),把巨大的图像矩阵切成很多小块。固定住其他块的变量,只把当前这一小块(比如 8 个变量)扔进 AOC 求解。AOC 一块一块的更新,如此循环迭代,最终拼出完整的大图。
规模(Scale): 目前的原型机只有 16 个物理节点(变量)。用数学方法(分块坐标下降 BCD)解决了如 20 万变量的 MRI 图像,但未来的目标是做成集成光子芯片,直接支持数百万变量。
速度(Speed): 目前受限于分立元件,每次循环大概 20纳秒 。如果集成到芯片上,速度能快 100 倍以上。
精度: 模拟计算总是有噪声的。虽然不动点机制能抗噪 ,但对于需要极高精度的科学计算,目前还不如数字计算机。
5. 结论与讨论 (Conclusion & Discussion)
模拟光学计算机(Analog Optical Computer, AOC)的核心突破在于通用性,能够在同一套模拟硬件上加速AI和组合优化任务。采用了一种光电混合架构,通过迭代反馈回路来寻找系统的"不动点" 。光学部分利用光的并行性处理计算量最大的矩阵-向量乘法 ;模拟电子部分则负责处理非线性激活、减法、动量以及退火等操作 。系统的物理演化过程本身就是计算过程,直到信号稳定在不动点,即为最终解 。通过四个实际应用案例展示了 AOC 的强大性能。