3.3 一般向量空间

csharp 复制代码

坐标系统是联系"矩阵变换"和"线性变换"的桥梁

1).基向量

向量空间R^n的基向量B: {v1, v2, v3...vn}, R^n空间中的向量都可以用基向量唯一表示

csharp 复制代码

基向量会充满整个R^n并且线性无关, 基向量的秩是n(列的维度), 基向量的行的维度也是n,

因此基向量是方阵; 又因为基向量线性无关, 因此基向量是逆矩阵

csharp 复制代码

2).坐标和坐标向量

csharp 复制代码

a.3, 4称为基向量中的坐标值

b.坐标向量是将3, 4组成的向量, 以"基向量为基准"的([V]b)

c.v = B * [v]b

- B是由基向量构成的矩阵

- [v]b是向量v在B中的坐标向量(列向量)

- v是标准坐标系的下的坐标

csharp 复制代码

3).坐标映射

当我们为一个向量空间V选定一组有序基B = {b1, b2,..., bn}, 这个空间中的每一个向量

v∈V都可以唯一地表示为这些基向量的线性组合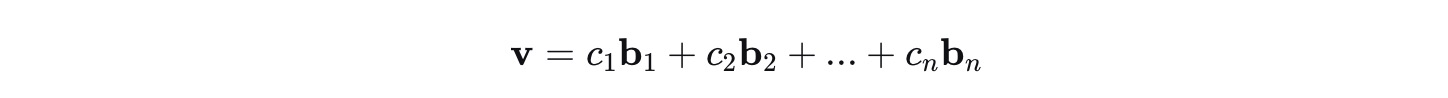

csharp 复制代码

我们将这组唯一确定的系数称为向量v在基向量B中的坐标向量

csharp 复制代码

"坐标映射是线性同构的"

a.线性性(保持加法和数乘)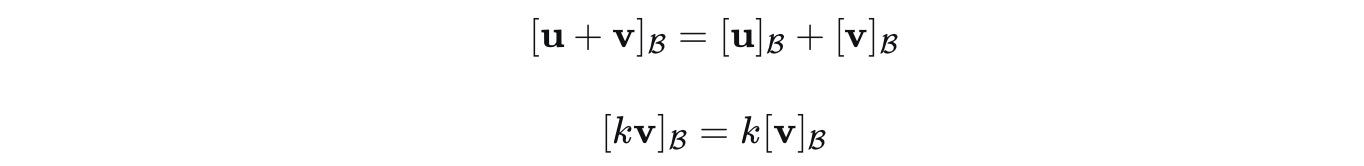

csharp 复制代码

向量空间V中的所有线性关系, 都会原封不动地体现在它的坐标表示中; 在V中做运算, 等同于

在R^n空间中做运算

b.双射性

csharp 复制代码

一个"一般向量空间中的向量", 可以是你能想到的任何东西, 只要它们能进行两种运算, 并且这

两种运算满足八条规则

这两种运算是:

加法: 两个向量可以相加, 得到另一个向量

数乘: 一个向量可以和一个标量(实数/复数)相乘, 得到另一个向量

注: "结果还在这个空间中"

csharp 复制代码

例1: 多项式空间

csharp 复制代码

例2: 矩阵空间