目录
[2.1 MemoryEncoder.forward](#2.1 MemoryEncoder.forward)
[2.1.6 PositionEmbeddingSine.forward](#2.1.6 PositionEmbeddingSine.forward)
一、前言
上一篇我们提到current_vision_feats会被self._encode_new_memory作为输入参数之一传入
current_vision_feats: [
torch.Size([65536, B, 32]),
torch.Size([16384, B, 64]),
torch.Size([4096, B, 256])
]
而_encode_new_memory会调用memory_encoder函数,也就是调用类MemoryEncoder里面的forward函数,MemoryEncoder.forward里面做了什么事呢?其实就是把torch.Size([B, 1, 1024, 1024])对象掩码图masks下采样后跟 torch.Size([B, 256, 64, 64])的图像特征图pix_feat进行融合。
pix_feat怎么来的,就是上面的current_vision_feats的最后一个torch.Size([4096, B, 256]) 变成torch.Size([B, 256, 64, 64])得来的。
下采样经历了什么,就是每次分辨率下降一半,1024->256->128->64,通道数乘4倍,1->4->16->64->256,也就是说分辨率下降一半造成的损失用增加4倍的通道数来弥补,这样就既不会对对象掩码图masks的特征造成过多的损失,又能把masks变成(B,256,64,64)的形状,这样就能跟pix_feat保持相同的尺寸以便进行融合,融合之后得到x。
然后有两条路,一条路是融合之后又经过fuser,又经过out_proj,out_proj里面把(B,256,64,64)变成了(B,64,64,64),得到了一个新的x,这个新的x就是融合了对象掩码的视觉特征,会被返回。
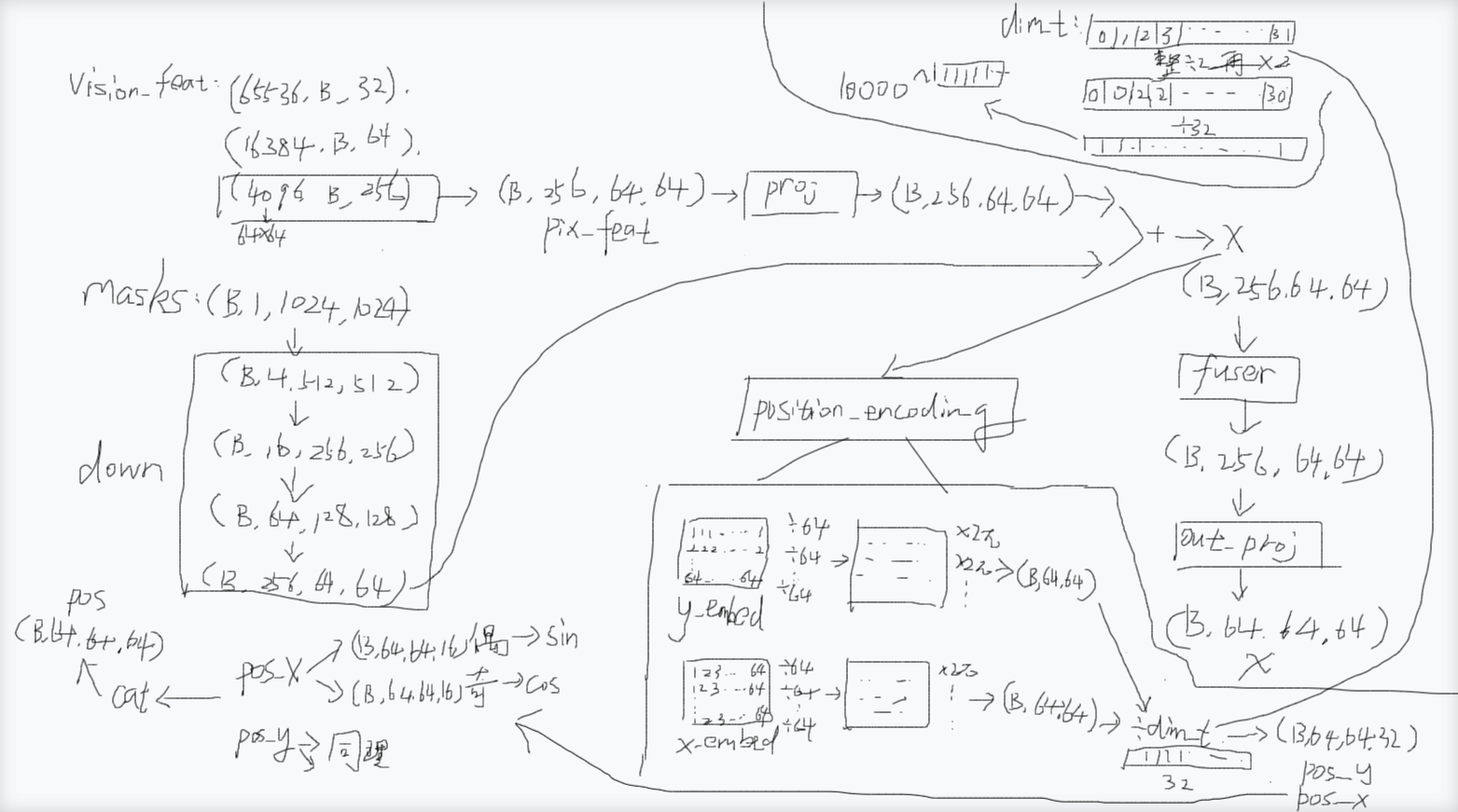
关于位置编码,因为有些物理概念我目前还没研究得特别清楚,所以也没完全搞清楚。怎么时间域和空间域有不同的物理量。
另一条路是x输入到position_encoding进行位置编码,位置编码就是transformer里面位置编码那一套,先整一个64x64的矩阵然后每行除以最大值64进行归一化,然后再乘以2π,此时的形状是(B,64,64), y方向和x方向都会做这个同理的操作,分别得到y_embed和x_embed,随后都会除以dim_t
dim_t是什么东西?我理解编码不同位置其实通过不同频率来编码的,dim_t是波长 λ 的归一化版本,它就是一个0,1,2,3...31的一维向量,每个元素整除2之后变成0,0,1,1...15的一维向量,为什么要整除以2,就是为了让相邻两个位置共用一个频率(波速相同的情况下,波长跟频率成反比关系),为什么相邻两个位置可以共用一个频率?因为相邻两个位置虽然用同一个频率,但随后一个会用sin,一个会用cos,并不冲突。然后再乘以2,然后除以32,为什么要除以32?就是想分成32个波长。最后就是这个一维向量作为指数中底数10000的幂,最终dim_t就变成底数为10000,指数为那32个元素的一维向量。为什么整成10000的幂这种呢?就是为了制造一组波长指数级增长的数值。
然后就是y_embed和x_embed分别除以dim_t(y_embed是(B,64,64)扩展到(B,64,64,1)再广播到(B,64,64,32)就可以除以32个元素了),上面这些操作可能就对应于pos / dim_t = 2π · pos / λ,然后就得到了pos_x和pos_y,它们都是(B,64,64,32),然后pos_x和pos_y各自都要进行这样一个操作:在偶数索引下计算sin,在奇数索引下计算cos,也就是一半用sin计算,一半用cos计算,相当于得到两个(B,64,64,16),就是(B,64,64,16,2),再合成后两个维度又变回(B,64,64,32)。由于pos_x和pos_y都会变成一个新的(B,64,64,32),它们cat连接之后变成(B,64,64,64)。
这样一来位置编码就能应对多尺度。其逻辑是**:**短波长 = 高频 = 区分近邻;长波长 = 低频 = 锚定全局。就是说一个像素的位置被编码成64维,32维x方向,32维y方向,32维度从高频到低频,高频就是说同一个周期(同样一段像素距离)下波长更短,频率更高,相邻像素的数值变化更大,所以能更好的区分邻近像素,低频则是像素之间要更远的距离才有较大变化的数值,所以能区分全局。如此一来,位置编码在局部到全局尺度下都能区分。
标准正弦波:sin(2π · pos / λ) = sin(ω · pos) # ω=2π/λ
位置编码: sin(pos / dim_t)
对比可得:
pos / dim_t = 2π · pos / λ
dim_t = [0, 1, 2, 3, 4, 5, 6, 7, ...]
dim_t // 2 = [0, 0, 1, 1, 2, 2, 3, 3, ...]
2 * (...) = [0, 0, 2, 2, 4, 4, 6, 6, ...]
(...) / 8 = [0, 0, 0.25, 0.25, 0.5, 0.5, 0.75, 0.75, ...]dim_t = 10000^[0, 0, 0.25, 0.25, 0.5, 0.5, 0.75, 0.75
, ...]= [1, 1, 10000^0.25, 10000^0.25, 10000^0.5, 10000^0.5, 10000^0.75, 10000^0.75]
= [1, 1, 10, 10, 100, 100, 1000, 1000]
波长(wavelength),是指波在一个振动周期内传播的距离。也就是沿着波的传播方向,相邻两个振动位相相差2π的点之间的距离。波长λ等于波速u和周期T的乘积,即λ=uT。同一频率的波在不同介质中以不同速度传播,所以波长也不同。

为什么我们有时看到ω=2π/λ,有时看到ω=2π/T?这不是同一个物理量
公式 符号 名称 定义域 单位 ω = 2π/Tω(omega) 角频率 时间域 rad/s k = 2π/λk(k) 角波数 空间域 rad/m ** 它们名字相似但完全不同**:
ω描述** 时间周期**,k描述**空间周期**。
时间域 vs 空间域:完整对应表
时间域(振动) ↔ 空间域(波动) ───────────────────────────────────────────── 时间 t ↔ 位置 x 周期 T(秒) ↔ 波长 λ(米) 频率 f = 1/T(Hz) ↔ 空间频率 = 1/λ(1/米) 角频率 ω = 2π/T ↔ 角波数 k = 2π/λ 相位 = ωt + φ₀ ↔ 相位 = kx + φ₀时间域 ↔ 空间域对应关系:
时间域(振动) 空间域(波动) 位置编码中的应用 时间 t 空间位置 x pos(像素坐标)周期 T(秒) 波长 λ(像素) dim_t(波长参数)频率 f(Hz) 空间频率(1/像素) 1/dim_t相位 ωt + φ₀相位 2πx/λ + φ₀pos/dim_t在 Transformer 位置编码中,我们用的是空间域公式:
PE(pos) = sin(pos / dim_t) # 这里的 dim_t 是波长 λ,不是周期 T位置编码本质上是多尺度的空间正弦波 ,
dim_t控制波长,pos/dim_t计算相
最后MemoryEndoder.foward会返回:
{
"vision_features": torch.Size([B, 64, 64, 64]) # 视觉特征x
"vision_pos_enc":: [torch.Size([B, 64, 64, 64])] # 位置编码[pos]
}
二、_encode_new_memory
2.1 MemoryEncoder.forward
sam2/modeling/memory_encoder.py
python
class MemoryEncoder(nn.Module):
"""
记忆编码器模块:用于将像素特征和对象掩码融合,生成带有位置编码的视觉特征。
该模块通常用于视频分割或对象跟踪任务中,对历史帧的信息进行编码。
"""
def __init__(
self,
out_dim,
mask_downsampler,
fuser,
position_encoding,
in_dim=256, # in_dim of pix_feats
):
"""
初始化记忆编码器
参数:
out_dim: 输出特征的维度
mask_downsampler: 掩码下采样模块,用于降低掩码的空间分辨率
fuser: 特征融合模块,用于融合像素特征和掩码信息
position_encoding: 位置编码模块,为特征添加空间位置信息
in_dim: 输入像素特征的维度,默认为256
"""
super().__init__()
# 掩码下采样器,用于将掩码调整到与特征图匹配的分辨率
self.mask_downsampler = mask_downsampler
# 像素特征投影层,将输入特征映射到统一维度空间
self.pix_feat_proj = nn.Conv2d(in_dim, in_dim, kernel_size=1)
# 特征融合模块,用于融合视觉特征和掩码信息
self.fuser = fuser
# 位置编码模块,为特征添加上下文位置信息
self.position_encoding = position_encoding
# 输出投影层,如果输入输出维度不同则进行维度转换
self.out_proj = nn.Identity()
if out_dim != in_dim:
self.out_proj = nn.Conv2d(in_dim, out_dim, kernel_size=1)
def forward(
self,
pix_feat: torch.Tensor,
masks: torch.Tensor,
skip_mask_sigmoid: bool = False,
) -> Tuple[torch.Tensor, torch.Tensor]:
"""
前向传播过程
参数:
pix_feat: 像素特征张量,形状通常为 [B, C, H, W]
masks: 对象掩码张量,形状通常为 [B, N, H, W],其中N是对象数量
skip_mask_sigmoid: 是否跳过对掩码的sigmoid操作,默认为False
返回:
字典包含:
- vision_features: 融合后的视觉特征 [B, out_dim, H, W]
- vision_pos_enc: 位置编码列表,包含空间位置信息
"""
# pix_feat: torch.Size([B, 256, 64, 64])
# masks: torch.Size([B, 1, 1024, 1024])
# skip_mask_sigmoid: True
## 处理掩码部分
# 对掩码应用sigmoid激活函数,使其值域在[0,1]之间
# 这样可以减少与真实掩码(布尔值)之间的域差异
if not skip_mask_sigmoid:
masks = F.sigmoid(masks)
# 通过下采样器调整掩码分辨率,使其与特征图尺寸匹配
# masks: torch.Size([B, 1, 1024, 1024])
# 经历四次下采样
# 每次空间分辨率/2 (1024->512->256->128->64), 通道数*4 (1->4->16->64->256)
masks = self.mask_downsampler(masks)
# masks: torch.Size([B, 256, 64, 64])
# 融合像素特征和下采样后的掩码
# 如果视觉特征在CPU上,将其转移到与掩码相同的设备(通常是CUDA)
pix_feat = pix_feat.to(masks.device)
# pix_feat: torch.Size([B, 256, 64, 64])
# 对像素特征进行投影,得到统一维度的特征表示
x = self.pix_feat_proj(pix_feat)
# x: torch.Size([B, 256, 64, 64])
# 将掩码信息加到特征图上,实现特征与掩码的融合
# 这里使用加法操作,让模型学习掩码区域的特征增强
x = x + masks
# x: torch.Size([B, 256, 64, 64])
# 通过融合模块进一步处理,增强特征表达能力
x = self.fuser(x)
# x: torch.Size([B, 256, 64, 64])
# 应用输出投影,调整最终输出维度
# Conv2d(256, 64, kernel_size=(1, 1), stride=(1, 1))
x = self.out_proj(x)
# x: torch.Size([B, 64, 64, 64])
# 生成位置编码,用于后续Transformer等模块的注意力计算
pos = self.position_encoding(x).to(x.dtype)
# pos: torch.Size([B, 64, 64, 64])
# {
# "vision_features": torch.Size([B, 64, 64, 64])
# "vision_pos_enc":: [torch.Size([B, 64, 64, 64])]
# }
# 返回包含视觉特征和位置编码的字典
return {"vision_features": x, "vision_pos_enc": [pos]}这段代码实现了一个**记忆编码器(MemoryEncoder)**模块,主要用于视频对象分割或跟踪任务中,将历史帧的视觉信息和对象掩码编码成具有空间位置感知的特征表示:
核心功能:
将像素级视觉特征与对象掩码进行有效融合
为融合后的特征添加位置编码,便于后续注意力机制处理
支持端到端的梯度传播和GPU加速
处理流程:
掩码处理:首先对输入掩码应用sigmoid激活(可选),然后通过下采样模块调整其空间分辨率,使其与特征图尺寸一致
特征对齐:将像素特征投影到统一维度空间,并自动处理设备(CPU/CUDA)不匹配问题
信息融合:通过加法操作将掩码信息注入特征图,然后通过专门的融合模块增强特征表达
维度转换:根据配置调整输出通道数
位置编码:生成空间位置信息,为后续Transformer等架构提供位置感知能力
设计特点:
模块化:将下采样、融合、位置编码等组件解耦,便于替换和扩展
灵活性:支持跳过sigmoid操作,适应不同的掩码输入格式
兼容性:自动处理设备迁移,确保不同张量在同一设备上运算
高效性:使用1x1卷积和恒等映射优化计算开销
该模块通常作为视频分割系统中的记忆库组件,用于编码历史帧信息,为当前帧的对象预测提供时序上下文支持。
2.1.6 PositionEmbeddingSine.forward
回到MemoryEncoder.forward
生成位置编码,用于后续Transformer等模块的注意力计算
pos = self.position_encoding(x).to(x.dtype)
sam2/modeling/position_encoding.py
python
class PositionEmbeddingSine(nn.Module):
"""
基于正弦函数的位置编码层,将像素坐标映射为高维特征向量。
这是对Transformer论文《Attention Is All You Need》中位置编码的2D扩展版本,
使其适用于图像特征图。核心思想是为每个空间位置生成唯一的、具有相对位置
感知能力的编码向量。
每个位置的编码由不同频率的正弦和余弦函数值组成,高频捕捉精细位置,
低频捕捉全局位置关系。
"""
def __init__(
self,
num_pos_feats, # 位置编码的特征维度(必须是偶数)
temperature: int = 10000, # 温度参数,控制频率范围
normalize: bool = True, # 是否将坐标归一化到[0, 2π]区间
scale: Optional[float] = None, # 归一化时的缩放因子
):
"""初始化位置编码器"""
super().__init__()
# 位置编码维度必须为偶数,因为一半给x坐标,一半给y坐标
assert num_pos_feats % 2 == 0, "Expecting even model width"
# 实际每个坐标(x或y)使用的特征维度
self.num_pos_feats = num_pos_feats // 2
self.temperature = temperature
self.normalize = normalize
# scale参数仅在normalize=True时有效,用于控制编码的幅度范围
if scale is not None and normalize is False:
raise ValueError("normalize should be True if scale is passed")
if scale is None:
# 默认使用2π作为坐标归一化的目标范围
scale = 2 * math.pi
self.scale = scale
# 缓存已计算过的位置编码,避免重复计算相同尺寸的特征图
self.cache = {}
def _encode_xy(self, x, y):
"""
内部方法:对归一化的x,y坐标进行正弦编码
参数:
x: x坐标的一维张量,已归一化到[0,1]区间
y: y坐标的一维张量,已归一化到[0,1]区间
返回:
pos_x: x坐标的编码结果 [len(x), num_pos_feats*2]
pos_y: y坐标的编码结果 [len(y), num_pos_feats*2]
"""
# 确保输入的x,y长度相同且为一维
assert len(x) == len(y) and x.ndim == y.ndim == 1
# 将坐标从[0,1]缩放到[0, scale]区间
x_embed = x * self.scale
y_embed = y * self.scale
# 生成维度索引,用于计算不同频率
# 公式: dim_t = temperature^(2i/d_model),i从0到num_pos_feats-1
dim_t = torch.arange(self.num_pos_feats, dtype=torch.float32, device=x.device)
dim_t = self.temperature ** (2 * (dim_t // 2) / self.num_pos_feats)
# 计算位置编码的原始值:坐标除以频率
# x_embed[:, None] 将形状从[N]变为[N,1],支持广播到[N, num_pos_feats]
pos_x = x_embed[:, None] / dim_t # 形状: [num_positions, num_pos_feats]
pos_y = y_embed[:, None] / dim_t
# 对每个维度的编码,偶数索引用sin,奇数索引用cos
# 这样可以生成不同频率的正弦和余弦值,捕捉多尺度位置信息
pos_x = torch.stack(
(pos_x[:, 0::2].sin(), pos_x[:, 1::2].cos()), dim=2
).flatten(1) # flatten将最后两维合并
pos_y = torch.stack(
(pos_y[:, 0::2].sin(), pos_y[:, 1::2].cos()), dim=2
).flatten(1)
return pos_x, pos_y
@torch.no_grad()
def encode_boxes(self, x, y, w, h):
"""
编码边界框:将中心坐标(x,y)和宽高(w,h)编码为位置特征
参数:
x, y: 边界框中心的归一化坐标 [N]
w, h: 边界框的宽高 [N]
返回:
pos: 编码结果 [N, num_pos_feats*4]
"""
# 先编码中心坐标
pos_x, pos_y = self._encode_xy(x, y)
# 将编码后的坐标与宽高信息拼接
# h[:, None] 增加一维以便拼接
pos = torch.cat((pos_y, pos_x, h[:, None], w[:, None]), dim=1)
return pos
encode = encode_boxes # 向后兼容旧版本
@torch.no_grad()
def encode_points(self, x, y, labels):
"""
编码点坐标:将点坐标(x,y)和标签编码为位置特征
参数:
x, y: 点的归一化坐标 [B, N]
labels: 点的标签 [B, N]
返回:
pos: 编码结果 [B, N, num_pos_feats*2+1]
"""
# 获取批大小和点数
(bx, nx), (by, ny), (bl, nl) = x.shape, y.shape, labels.shape
assert bx == by and nx == ny and bx == bl and nx == nl # 维度一致性检查
# 展平后编码,再恢复原始形状
pos_x, pos_y = self._encode_xy(x.flatten(), y.flatten())
pos_x, pos_y = pos_x.reshape(bx, nx, -1), pos_y.reshape(by, ny, -1)
# 拼接编码后的坐标和标签
pos = torch.cat((pos_y, pos_x, labels[:, :, None]), dim=2)
return pos
@torch.no_grad()
def forward(self, x: torch.Tensor):
"""
前向传播:为输入特征图的每个像素生成位置编码
参数:
x: 输入特征图 [B, C, H, W]
返回:
pos: 位置编码 [B, num_pos_feats*2, H, W]
"""
# x: torch.Size([B, 64, 64, 64])
# 使用(H,W)作为缓存键,避免重复计算相同尺寸的特征图
cache_key = (x.shape[-2], x.shape[-1])
# cache_key: (64, 64)
# self.cache:{}
if cache_key in self.cache:
# 从缓存中读取并重复batch维度
return self.cache[cache_key][None].repeat(x.shape[0], 1, 1, 1)
# 生成y方向坐标:[[1,2,3,...,H]]重复W次
# view和repeat操作创建完整坐标网格
y_embed = (
torch.arange(1, x.shape[-2] + 1, dtype=torch.float32, device=x.device) # [H]
.view(1, -1, 1) # [1, H, 1]
.repeat(x.shape[0], 1, x.shape[-1]) # [B, H, W]
)
# y_embed: torch.Size([B, 64, 64]) 第1行64个1,第2行64个2....第64行64个64
# 生成x方向坐标:[[1,2,3,...,W]]重复H次
x_embed = (
torch.arange(1, x.shape[-1] + 1, dtype=torch.float32, device=x.device) # [W]
.view(1, 1, -1) # [1, 1, W]
.repeat(x.shape[0], x.shape[-2], 1) # [B, H, W]
)
# x_embed:torch.Size([B, 64, 64]) 64行都是[1,2,...64]
# 将坐标归一化到[0, scale]区间
# 除以最大值并乘以scale,使坐标范围从[1, H/W]变为[0, scale]
# self.normalize:True
if self.normalize:
eps = 1e-6 # 防止除零
# self.scale: 6.283185307179586
y_embed = y_embed / (y_embed[:, -1:, :] + eps) * self.scale
# y_embed :torch.Size([B, 64, 64]) 数值都在0到2π
x_embed = x_embed / (x_embed[:, :, -1:] + eps) * self.scale
# x_embed:torch.Size([B, 64, 64]) 数值都在0到2π
# 生成频率维度,用于不同尺度的正弦编码
# self.num_pos_feats: 32
dim_t = torch.arange(self.num_pos_feats, dtype=torch.float32, device=x.device)
# dim_t: tensor([0,1,2,...,31], device='cuda:0')
# 温度参数控制频率范围,temperature越大,频率变化越慢
# self.temperature: 10000
dim_t = self.temperature ** (2 * (dim_t // 2) / self.num_pos_feats)
# dim_t: torch.Size([32])
# dim_t: tensor([1.0000e+00, 1.0000e+00, 1.7783e+00, ...])
# 计算位置编码:坐标除以频率
# 增加一维以便广播: [B, H, W, 1] / [num_pos_feats] -> [B, H, W, num_pos_feats]
pos_x = x_embed[:, :, :, None] / dim_t
# pos_x: torch.Size([B, 64, 64, 32])
pos_y = y_embed[:, :, :, None] / dim_t
# pos_y: torch.Size([B, 64, 64, 32])
# 对每个维度的编码,偶数索引用sin,奇数索引用cos
# 这样每个位置得到唯一的编码,且编码具有相对位置感知能力
pos_x = torch.stack(
(pos_x[:, :, :, 0::2].sin(), pos_x[:, :, :, 1::2].cos()), dim=4
).flatten(3) # 合并sin/cos维度
# pos_x: torch.Size([B, 64, 64, 32])
pos_y = torch.stack(
(pos_y[:, :, :, 0::2].sin(), pos_y[:, :, :, 1::2].cos()), dim=4
).flatten(3)
# pos_y: torch.Size([B, 64, 64, 32])
# 拼接y和x的编码,并调整维度顺序
# permute将维度从[B, H, W, C]变为[B, C, H, W],符合特征图格式
pos = torch.cat((pos_y, pos_x), dim=3).permute(0, 3, 1, 2)
# pos: torch.Size([B, 64, 64, 64])
# 缓存第一个样本的编码,供后续相同尺寸的batch复用
self.cache[cache_key] = pos[0]
# self.cache:{(64, 64): torch.Size([64, 64, 64])}
# pos: torch.Size([B, 64, 64, 64])
return pos这个
PositionEmbeddingSine类实现了基于正弦函数的位置编码,是Transformer架构在计算机视觉任务中的关键组件:核心设计思想
借鉴《Attention Is All You Need》的位置编码方案,为2D特征图的每个像素生成唯一且相对位置敏感的编码向量,使模型能够感知空间位置关系。
工作流程
坐标网格生成 :为输入特征图的每个像素生成整数坐标网格
[1..H]和[1..W]坐标归一化 :将坐标缩放到
[0, 2π]区间,消除不同尺寸特征图的尺度差异频率生成:通过温度参数创建从低频到高频的多个正弦/余弦频率
位置编码计算 :每个坐标的编码是多个频率下
sin和cos值的组合维度拼接:将x和y方向的编码拼接,形成最终的2D位置特征
关键特性
特性 说明 作用 正弦编码 PE(pos,2i) = sin(pos/10000^(2i/d))PE(pos,2i+1) = cos(pos/10000^(2i/d))生成唯一编码,支持相对位置计算 多频率 从低频到高频覆盖不同尺度 高频捕捉精细位置,低频捕捉全局结构 归一化 坐标先归一化到固定范围 使编码对特征图尺寸不敏感 缓存机制 相同尺寸的特征图复用编码 大幅提升推理效率 偶数维度 编码维度(num_pos_feats)必须为偶数 确保sin/cos能配对使用 数学公式
位置编码的核心公式来自Transformer论文:
PE(pos, 2i) = sin(pos / 10000^(2i/d_model)) PE(pos, 2i+1) = cos(pos / 10000^(2i/d_model))其中
pos是归一化后的坐标,i是特征维度索引,d_model是编码维度。应用场景
目标检测:为DETR等检测器提供空间位置信息
视频分割:让模型知道哪些像素属于时序中的哪个空间位置
图像生成:在扩散模型中保持空间结构一致性
SAM (Segment Anything):为图像编码器提供位置感知能力
缓存优化
通过
self.cache存储已计算过的尺寸编码,避免对相同分辨率的重复计算,在视频处理中显著加速(连续帧通常分辨率相同)。
y_embed = (
torch.arange(1, x.shape[-2] + 1, dtype=torch.float32, device=x.device) # [H]
.view(1, -1, 1) # [1, H, 1]
.repeat(x.shape[0], 1, x.shape[-1]) # [B, H, W]
)
这什么意思?解释一下语法
这段代码是 PyTorch 链式调用 的写法,用于生成 y 方向(高度方向)的坐标网格。让我逐行拆解语法和含义:
整体功能
创建一个形状为
[B, H, W]的张量,其中每个元素值等于其 y 坐标(从1开始计数)。
逐行语法解释
y_embed = ( torch.arange(1, x.shape[-2] + 1, dtype=torch.float32, device=x.device) # [H] .view(1, -1, 1) # [1, H, 1] .repeat(x.shape[0], 1, x.shape[-1]) # [B, H, W] )1.
torch.arange(...)- 创建基础坐标
torch.arange(1, x.shape[-2] + 1, dtype=torch.float32, device=x.device)
**
x.shape[-2]**: 获取特征图的 ** 高度 H ****
torch.arange(1, H+1)**: 生成一维张量[1, 2, 3, ..., H]**
dtype=torch.float32**: 指定浮点数类型(后续计算需要)**
device=x.device**: 确保与输入张量 ** 在同一设备 **(CPU或GPU)** 结果形状 **:
[H](一维向量)** 2.
.view(1, -1, 1)- 重塑形状 **
.view(1, -1, 1)
**
.view(): PyTorch 的 形状重塑 方法, 不复制数据 **,只改变视图**
1, -1, 1**:
第0维:
1(Batch维度)第1维:
-1(自动推断,这里是H)第2维:
1(宽度维度占位)** 结果形状 **:
[1, H, 1](三维张量)** 示例 **:
[1, 2, 3, 4]→view(1, -1, 1)→[[[1], [2], [3], [4]]]3.
.repeat(B, 1, W)- 复制扩展
.repeat(x.shape[0], 1, x.shape[-1])
**
.repeat(): 在 指定维度上复制 **数据(会分配新内存)** 参数含义 **:
x.shape[0]: ** Batch 大小 B **,在Batch维度重复B次
1: 在H维度** 不重复 **(保持原样)
x.shape[-1]: ** 宽度 W **,在宽度维度重复W次** 结果形状 **:
[B, H, W]** 数据内容 **: 每行都是相同的y坐标值
** 示例 **:
[[[1], [2]]]+.repeat(2, 1, 3)→
[[[1,1,1], [2,2,2]], [[1,1,1], [2,2,2]]] # 2个batch,每个都是2x3的网格
完整执行过程示例
假设输入
x的形状是[2, 256, 4, 4](B=2, H=4, W=4):
# Step 1: torch.arange(1, 4+1) → tensor([1., 2., 3., 4.]) 形状[4] # Step 2: .view(1, -1, 1) → tensor([[[1.], [2.], [3.], [4.]]]) 形状[1,4,1] # Step 3: .repeat(2, 1, 4) → tensor([[[1., 1., 1., 1.], [2., 2., 2., 2.], [3., 3., 3., 3.], [4., 4., 4., 4.]], [[1., 1., 1., 1.], [2., 2., 2., 2.], [3., 3., 3., 3.], [4., 4., 4., 4.]]]) # 形状[2,4,4]
对应代码块
# 生成的 y_embed 是每个像素的y坐标 y_embed = [[[1,1,1,1], x_embed = [[[1,2,3,4], [2,2,2,2], [1,2,3,4], [3,3,3,3], [1,2,3,4], [4,4,4,4]]] [1,2,3,4]]] # 后续会将它们归一化并编码,最终得到位置编码与 x_embed 的区别
x_embed = ( torch.arange(1, x.shape[-1] + 1, ...) # [W] = [1,2,3,4] .view(1, 1, -1) # [1, 1, W] .repeat(x.shape[0], x.shape[-2], 1) # [B, H, W] )
x_embed生成的是 ** x方向坐标 **,每列相同两者配合为每个像素提供 ** (x, y) ** 完整坐标
核心语法点总结
语法 作用 是否分配新内存 torch.arange()创建等差数列 是 .view()重塑形状 ** 否 **(仅改变视图) .repeat()复制数据 ** 是 **(深拷贝) x.shape[-2]取倒数第二维(H) - [:, None, None]维度扩展(等同于 .unsqueeze())否 这段代码是 ** 位置编码 ** 的经典实现,通过重复和广播高效生成坐标网格,为后续的正弦编码做准备。
y_embed = y_embed / (y_embed[:, -1:, :] + eps) * self.scale
y_embed :torch.Size([B, 64, 64]) 数值都在0到2π
x_embed = x_embed / (x_embed[:, :, -1:] + eps) * self.scale
x_embed:torch.Size([B, 64, 64]) 数值都在0到2π
什么意思?
这两行代码是坐标归一化 操作,将 整数坐标 转换为** 相对位置**([0, 1] 范围),再缩放到目标范围(通常是
[0, 2π])。让我一步步拆解:
代码作用总览
y_embed = y_embed / (y_embed[:, -1:, :] + eps) * self.scale x_embed = x_embed / (x_embed[:, :, -1:] + eps) * self.scale**目标 **: 将原始坐标
[1, 2, 3, ..., H]转换为[0, scale]区间的归一化坐标。
逐行拆解
** y_embed 的归一化 **
y_embed / (y_embed[:, -1:, :] + eps) * self.scale1.
y_embed[:, -1:, :]- 获取最后一行
# 假设 y_embed 形状: [B, 64, 64] # y_embed[:, -1:, :] 取最后一个行,形状: [B, 1, 64] # 示例(B=1, H=4, W=4): y_embed = [[[1,1,1,1], [2,2,2,2], [3,3,3,3], [4,4,4,4]]] # 形状[1,4,4] y_embed[:, -1:, :] = [[[4,4,4,4]]] # 形状[1,1,4],最后一个值是H=42.
+ eps- 防止除零
+ 1e-6 # 避免除以0的数值稳定性保护3.
/ ( ... )- 归一化到 [0, 1]
# 每个元素除以该维度的最大值(最后一行的值) # 示例: y_embed = [[[1,1,1,1], /4 = [[[0.25, 0.25, 0.25, 0.25], [2,2,2,2], /4 [0.5 , 0.5 , 0.5 , 0.5 ], [3,3,3,3], /4 [0.75, 0.75, 0.75, 0.75], [4,4,4,4]]] /4 [1.0 , 1.0 , 1.0 , 1.0 ]]]4.
* self.scale- 缩放到目标范围
self.scale = 2 * math.pi ≈ 6.283 # 结果: [[[0.25*2π, 0.25*2π, ...], = [[[π/2, π/2, π/2, π/2], [0.5 *2π, 0.5 *2π, ...], [π , π , π , π ], [0.75*2π, 0.75*2π, ...], [3π/2, 3π/2, ...], [1.0 *2π, 1.0 *2π, ...]]] [2π , 2π , 2π , 2π ]]]
** x_embed 的归一化 **
x_embed[:, :, -1:] # 取最后一列,形状: [B, 64, 1]逻辑完全相同,只是操作维度不同:
原始
x_embed:[[[1,2,3,4], [1,2,3,4], ...]]# 每列是坐标取最后一列:
[[[4], [4], [4], ...]]# 最大值W=4归一化结果:
[[[0.25,0.5,0.75,1.0], ...]]# 每行是0到1
完整示例(H=4, W=4, scale=2π)
归一化前
y_embed = [[[1, 1, 1, 1], x_embed = [[[1, 2, 3, 4], [2, 2, 2, 2], [1, 2, 3, 4], [3, 3, 3, 3], [1, 2, 3, 4], [4, 4, 4, 4]]] [1, 2, 3, 4]]]归一化后
y_embed = [[[0.25π, 0.25π, 0.25π, 0.25π], [0.5π , 0.5π , 0.5π , 0.5π ], [0.75π, 0.75π, 0.75π, 0.75π], [1.0π , 1.0π , 1.0π , 1.0π ]]] x_embed = [[[0.25π, 0.5π , 0.75π, 1.0π ], [0.25π, 0.5π , 0.75π, 1.0π ], [0.25π, 0.5π , 0.75π, 1.0π ], [0.25π, 0.5π , 0.75π, 1.0π ]]]
为什么要这样做?
1. 尺寸不变性(Scale Invariance)
无论输入是
64x64还是512x512,归一化后坐标都在[0, 2π]区间:
模型学到的位置编码模式与图像尺寸无关
泛化能力更强
2. 频率范围控制
正弦编码的公式是
sin(pos / temperature^(2i/d)):
如果
pos是原始像素值(如1..512),高频分量会迅速饱和归一化到
[0, 2π]确保频率分布在有效范围内3. 数值稳定性
避免大数值坐标(如512, 1024)导致指数运算溢出
temperature=10000配合[0, 2π]生成合理的频率范围4. 相对位置保持
归一化后,** 相对位置关系**仍然保留:
左上角的点永远是
(0, 0)右下角的点永远是
(2π, 2π)模型可以更稳定地学习空间关系
核心语法点
语法 含义 作用 [:, -1:, :]取倒数第二个维度的最后一个元素 获取该维度的最大值 [:, :, -1:]取最后一个维度的最后一个元素 获取该维度的最大值 + eps加极小值防止除零 数值稳定性保护 / max每个元素除以最大值 归一化到 [0, 1] * scale乘以缩放因子 映射到目标范围 这两行代码是位置编码的预处理核心,确保不同尺寸的输入都能被编码到统一的分布空间。
y_embed / (y_embed[:, -1:, :] + eps) * self.scale 一个矩阵除以一行数据,python语法为什么是允许的呢?
PyTorch 允许这种"形状不同 "的张量运算,靠的不是 Python 语法本身,而是 PyTorch 的广播机制(broadcasting) 。
只要两个张量的形状满足广播规则,运算就会自动、隐式地把较小的那个张量"复制扩展"到与较大的张量一致,然后再做逐元素运算。
1. 广播规则(Broadcasting Rule)
(官方文档:torch.broadcast)
从右往左逐维比较:
条件 说明 ① 维度相等 任意一方 dim == 1也算相等② 维度大小相等 或者有一方 dim == 1只要每一维都满足上面任意一条,就可以广播。
2. 你的例子拆解
假设运行时:
y_embed.shape # [B, H, W] 例如 [2, 64, 64] y_embed[:, -1:, :] # [B, 1, W] 例如 [2, 1, 64]维度对比(从右往左):
维度 张量 A 张量 B 是否满足 最右 64 64 ✅ 相等 中间 64 1 ✅ 有一方为 1 最左 2 2 ✅ 相等 → 广播合法 ,PyTorch 会自动把
[B, 1, W]沿H维复制H次,变成[B, H, W],然后做逐元素除法。
3. 广播过程可视化(小例子)
import torch a = torch.arange(1, 5).view(2, 2).float() # [[1, 2], [3, 4]] b = a[:, -1:, :] # [[3, 4]] shape(1, 2) c = a / b print(c)内部广播:
a: [[1, 2], b: [[3, 4]] → 复制为 [[3, 4], [3, 4]] [3, 4]]结果:
c = [[1/3, 2/4], [3/3, 4/4]] = [[0.3333, 0.5], [1.0, 1.0]]
4. 回到你的代码
y_embed = y_embed / (y_embed[:, -1:, :] + eps) * self.scale广播步骤:
y_embed[:, -1:, :]→ 形状[B, 1, W]
+ eps→ 仍是[B, 1, W]PyTorch 自动把它沿 H 维广播 成
[B, H, W]做逐元素除法 → 结果形状保持
[B, H, W]语义 :
把每一行的 y 坐标都除以该 batch、该列的最大值 (即最后一行的值),从而把坐标归一化到
[0, 1],再乘以self.scale得到[0, 2π]。
5. 小结
不是 Python 原生语法 ,而是 PyTorch 广播机制
只要维度满足"从右往左逐维相等或有一方为 1"即可
运算时会隐式复制数据,不额外分配大量内存(视图 + 广播)
因此"矩阵 ÷ 一行"或"矩阵 ÷ 一列"在 PyTorch 里都是合法且高效的单行写法
dim_t = torch.arange(self.num_pos_feats, dtype=torch.float32, device=x.device)
dim_t = self.temperature ** (2 * (dim_t // 2) / self.num_pos_feats)
什么意思?
这两行代码是位置编码的频率生成核心,用于创建不同波长的正弦/余弦函数。让我一步步拆解:
代码目的总览
dim_t = self.temperature ** (2 * (dim_t // 2) / self.num_pos_feats)这行代码计算的是** 分母中的频率项 **,即
10000^(2i/d_model),控制不同维度上的波长。
逐行拆解
** 1.
dim_t = torch.arange(...)**
dim_t = torch.arange(self.num_pos_feats, dtype=torch.float32, device=x.device)
作用 : 生成 维度索引 数组
[0, 1, 2, 3, ..., num_pos_feats-1]示例 : 若
num_pos_feats=8,则dim_t = [0, 1, 2, 3, 4, 5, 6, 7]
2.
dim_t // 2- 整数除法(核心技巧)
dim_t // 2
作用 : 将相邻两个维度映射到 同一个索引值 ,实现
sin/cos配对** 示例**:
dim_t = [0, 1, 2, 3, 4, 5, 6, 7] dim_t // 2 = [0, 0, 1, 1, 2, 2, 3, 3] ^ ^ ^ ^ ^ ^ ^ ^ | | | | | | | | 对应sin/cos s c s c s c s c为什么这样做? : 确保
PE(pos, 2i)和PE(pos, 2i+1)使用 相同的频率 ,只是一个是sin,一个是cos
** 3.
2 * (dim_t // 2) / self.num_pos_feats**
2 * (dim_t // 2) / self.num_pos_feats这是** 指数部分的分子**,设计目的是让频率** 指数级衰减 **。
** 计算示例 **(
num_pos_feats=8):
pythondim_t // 2 = [0, 0, 1, 1, 2, 2, 3, 3] 2 * (...) = [0, 0, 2, 2, 4, 4, 6, 6] (...) / 8 = [0, 0, 0.25, 0.25, 0.5, 0.5, 0.75, 0.75]** 数学意义 :
2i / d_model,其中i是维度索引的 一半 **
i = 0 → 2i/d = 0/8 = 0 i = 1 → 2i/d = 2/8 = 0.25 i = 2 → 2i/d = 4/8 = 0.5 i = 3 → 2i/d = 6/8 = 0.75
** 4.
self.temperature ** (...)**
self.temperature ** (...)
**
temperature=10000: 控制 频率范围 **的底数作用 : 生成 从低频到高频的指数级变化的频率
完整计算示例 (
num_pos_feats=8,temperature=10000):
python指数部分 = [0, 0, 0.25, 0.25, 0.5, 0.5, 0.75, 0.75] dim_t = 10000^[0, 0, 0.25, 0.25, 0.5, 0.5, 0.75, 0.75] = [1, 1, 10000^0.25, 10000^0.25, 10000^0.5, 10000^0.5, 10000^0.75, 10000^0.75] = [1, 1, 10, 10, 100, 100, 1000, 1000]
最终
dim_t的物理意义
dim_t是位置编码的分母 ,即波长:
pos_x = x_embed / dim_t
dim_t值含义 对应周期 作用 1 最短波长,对应最高频 2π 捕捉极精细位置 10 较短波长,对应高频 20π 捕捉局部位置 100 中等波长,对应中频 200π 捕捉区域位置 1000 最长波长,对应低频 2000π 捕捉全局位置
完整流程示例
假设
x_embed=π(位置在高度中间):
python# dim_t = [1, 1, 10, 10, 100, 100, 1000, 1000] pos_x = π / dim_t = [3.14, 3.14, 0.314, 0.314, 0.0314, 0.0314, 0.00314, 0.00314] # 经过 sin/cos 后: sin(pos_x) = [0.0016, 0.0016, 0.309, 0.309, 0.0314, 0.0314, 0.00314, 0.00314] cos(pos_x) = [-0.9999, -0.9999, 0.951, 0.951, 0.9995, 0.9995, 0.999995,0.999995]
为什么这样设计?
多尺度位置感知:不同频率捕捉不同尺度的位置关系
高频:区分相邻像素
低频:区分远距离像素
相对位置计算 :这种编码方式使得
PE(pos+k)可以表示为PE(pos)和PE(k)的线性函数,便于注意力机制学习相对位置
Transformer原始设计 :直接沿用论文中的
10000^(2i/d_model),在大规模语料上验证有效sin/cos配对:使用相同频率生成 sin 和 cos,能唯一确定相位,避免位置冲突
这两行代码是整个位置编码的数学核心,通过优雅的频率设计让模型以不同粒度感知空间位置。
计算位置编码:坐标除以频率
增加一维以便广播: [B, H, W, 1] / [num_pos_feats] -> [B, H, W, num_pos_feats]
pos_x = x_embed[:, :, :, None] / dim_t
pos_x: torch.Size([B, 64, 64, 32])
pos_y = y_embed[:, :, :, None] / dim_t
pos_y: torch.Size([B, 64, 64, 32])
对每个维度的编码,偶数索引用sin,奇数索引用cos
这样每个位置得到唯一的编码,且编码具有相对位置感知能力
pos_x = torch.stack(
(pos_x[:, :, :, 0::2].sin(), pos_x[:, :, :, 1::2].cos()), dim=4
).flatten(3) # 合并sin/cos维度
pos_x: torch.Size([B, 64, 64, 32])
pos_y = torch.stack(
(pos_y[:, :, :, 0::2].sin(), pos_y[:, :, :, 1::2].cos()), dim=4
).flatten(3)
pos_y: torch.Size([B, 64, 64, 32])
拼接y和x的编码,并调整维度顺序
permute将维度从[B, H, W, C]变为[B, C, H, W],符合特征图格式
pos = torch.cat((pos_y, pos_x), dim=3).permute(0, 3, 1, 2)
什么意思?
这段代码把"归一化后的 x、y 坐标"变成最终能拿来加在特征图上的位置编码张量 。
一句话:先算 sin/cos,再拼成 2D 位置特征,最后调成 CNN 喜欢的通道优先格式。
下面按执行顺序拆给你看(以 B=1, H=W=64, num_pos_feats=32 为例):
1️⃣ 坐标 ÷ 波长→ 拿到"角度(弧度)"
pos_x = x_embed[:, :, :, None] / dim_t # [B, 64, 64, 32] pos_y = y_embed[:, :, :, None] / dim_t # [B, 64, 64, 32]
x_embed形状[B, 64, 64],最后一维加 1 变成[B, 64, 64, 1]
dim_t形状[32](频率向量)广播 → 每个像素位置都得到 32 个"角度值"
结果:每张图每个像素都有 32 个不同波长的"相位"。
2️⃣ sin/cos 交错 → 生成唯一编码
pos_x = torch.stack( (pos_x[:, :, :, 0::2].sin(), pos_x[:, :, :, 1::2].cos()), dim=4 ).flatten(3)
0::2取偶数索引做 sin,1::2取奇数索引做 cos
stack(..., dim=4)把 sin/cos 拼成新的一维 → 形状[B, 64, 64, 16, 2]
flatten(3)把最后两维压平 → 恢复[B, 64, 64, 32]
效果 :每 2 个通道一组(sin, cos),保持 Transformer 原论文的"正弦-余弦对"设计,使编码具有相对位置可分解性。对
pos_y做同样操作,得到另一组 32 通道。
3️⃣ 拼接 x、y 方向 → 2D 位置特征
pos = torch.cat((pos_y, pos_x), dim=3) # [B, 64, 64, 64]
沿最后一维(通道维)把 y 编码与 x 编码拼起来
总共 64 通道 = 32 (y) + 32 (x)
4️⃣ 调换维度顺序 → CNN 标准格式
pos = pos.permute(0, 3, 1, 2) # [B, 64, 64, 64]
从
[B, H, W, C]→[B, C, H, W]这样后续可以直接
feature_map + pos或torch.cat([feature, pos], dim=1),无需额外转置。
结果
得到张量
pos形状[B, 64, 64, 64],其中:
每个像素都有 64 维向量
前 32 维是 y 方向的正弦-余弦混合编码
后 32 维是 x 方向的正弦-余弦混合编码
不同像素的向量不同,且满足"相对位置=可分解"的数学性质,方便注意力机制学习。
这就是最终能与图像特征逐像素相加的 2D 位置编码。
为什么坐标 ÷ 波长 → 拿到"角度"? 每张图每个像素都有 32 个不同波长的"相位"是什么意思?什么是波长?什么是相位?为什么每个像素要64维向量,前 32 维是 y 方向的正弦-余弦混合编码,后 32 维是 x 方向的正弦-余弦混合编码,是因为针对64x64的图才能保证位置编码唯一性吗?
这几个问题触及了位置编码的数学本质。我一层层解释:
1. 为什么坐标 ÷ 波长 → 拿到"角度"?
pos_x = x_embed / dim_t
x_embed:归一化坐标(单位:弧度,范围 0~2π)
dim_t:波长参数(单位:像素,范围 1~10000)
pos_x:相位角(单位:弧度,表示在该波长下的位置)物理意义 :像素位置在不同尺度的正弦波上处于什么相位。就像在一条波长为10米的波上,你站在3米处,相位就是 3/10 × 2π。
每张图每个像素都有 32 个不同波长的"相位"是什么意思?
每个像素 (如坐标
(20, 30))在 32 个不同波长(dim_t[0]~dim_t[31])
各有一个相位角(pos_x, pos_y)
经过 sin/cos 后得到 32 维编码向量
类比:像素同时参与 32 支不同节奏的舞蹈,每支舞的节奏(波长)不同,它在每支舞中的站位(相位)也不同。
举例:
x_embed = 3.14 # 像素位置(已归一化到[0, 2π]) dim_t = [1, 10, 100, 1000] # 波长参数(单位:像素) # 计算相位角(弧度) pos_x = 3.14 / [1, 10, 100, 1000] = [3.14, 0.314, 0.0314, 0.00314] # 对应sin/cos值: sin: [0.0016, 0.309, 0.0314, 0.00314] # 不同精度的位置特征 cos: [-0.9999, 0.951, 0.9995, 0.999995]
2. "波长" 和 "相位" 是什么意思?
概念 数学定义 在位置编码中的作用 波长 λ 正弦函数一个完整周期所覆盖的像素数 控制位置感的粗细粒度 相位 φ 在某个像素上,正弦波处于周期的哪个角度: φ = 2π × 像素位置 / λ唯一确定该像素在该波长下的特征值 关系式:
phase_angle = pos / dim_t # 弧度
sin_value = sin(phase_angle) # 编码值
总结
x_embed/y_embed是像素坐标,dim_t是波长参数,坐标除以波长得到相位角,经过 sin/cos 后生成多尺度位置编码,64维是超参数选择,与图像尺寸无关。
波长 (Wavelength)正弦函数走完一个完整周期(从 0 到 2π)对应的空间距离。
低频 (如
dim_t=1000):波长很长(≈6283),在64x64图上几乎不变 → 捕捉全局/粗粒度位置高频 (如
dim_t=1):波长很短(≈6.28),在图上快速振荡 → 捕捉局部/细粒度位置相位 (Phase)
在某个具体位置上,正弦波处于周期的哪个阶段。
# 位置0.1π和位置0.9π的相位不同 sin(0.1π) = 0.309 # 上升阶段 sin(0.9π) = 0.951 # 接近峰值32个不同波长 = 32个不同尺度的"尺子" 同时测量位置,有的看整体,有的看局部。
为什么每个像素要64维向量?是唯一性必需的吗?
64维的构成
64维 = 32维(y方向) + 32维(x方向) = [sin(y/1), cos(y/1), sin(y/10), cos(y/10), ..., sin(y/10000), cos(y/10000), sin(x/1), cos(x/1), sin(x/10), cos(x/10), ..., sin(x/10000), cos(x/10000)]为什么是64?------ 与图像尺寸无关!
这不是为64x64图设计的:
维度选择 是模型容量 的权衡:32对 sin/cos 足以编码任意尺寸图像的相对和绝对位置
即使1024x1024的图 ,64维也足够,因为编码不是存坐标,而是学习位置的模式
维度太少:高频不足,无法区分相邻像素
维度太多:冗余,增加计算负担
唯一性保证
64维能保证唯一性,靠的是数学原理,而非维度数=图像尺寸:
关键点 :不同频率的
sin/cos组合构成一个高维空间中的唯一坐标。
# 假设只有2个频率(频率1和10),足以解释原理 位置 (x=0.3π, y=0.7π) 的编码: y_enc = [sin(0.7π), cos(0.7π), sin(0.07π), cos(0.07π)] x_enc = [sin(0.3π), cos(0.3π), sin(0.03π), cos(0.03π)] 总编码 = [0.588, -0.809, 0.218, 0.976, 0.809, 0.588, 0.094, 0.996]唯一性来源:
sin/cos配对 :仅用
sin(y)无法区分y和π-y(因为sin(y)=sin(π-y)),但加上cos(y)就能唯一确定角度。多频率 :每个频率提供不同周期 的约束,像多层密码,组合后几乎不可能冲突。
线性代数视角 :只要频率选择合理,映射
f: (x, y) → R^64是单射(injective),不同输入对应不同输出。
4. 为什么前32维是y,后32维是x?
设计考量
pos = torch.cat((pos_y, pos_x), dim=3) # [B, H, W, 64]
解耦性 :y和x方向独立编码,模型可以分别学习垂直 和水平位置模式
对称性:两个方向用相同编码函数,符合图像的各向同性
拼接顺序:只是约定俗成,先y后x或先x后y都可以,只要模型训练时一致
能否反过来?
完全可以:
pos = torch.cat((pos_x, pos_y), dim=3) # [B, H, W, 64]只要整个模型统一使用这个顺序,效果等价。
self.temperature为什么设置为10000?32对 sin/cos 足以编码任意尺寸图像的相对和绝对位置这个有什么依据?我还是没理解dim_t的大小,跟 捕捉全局/粗粒度位置和捕捉局部/细粒度位置的推理逻辑在哪?
问题1:为什么
temperature=10000?
dim_t = temperature^(2i / d_model)设计目标 :让波长 λ = 2π·dim_t 在 对数尺度 上均匀覆盖 1 到约 10,000 像素。
为什么选择10000?
下限 1 :最短波长 2π·1 ≈ 6.28 像素,能区分相邻像素
上限 10000 :最长波长 2π·10000 ≈ 62,800 像素,在大图像中仍缓慢变化,提供全局锚点
对数均匀 :像素位置从 1 到 10000 跨越 4个数量级,覆盖所有尺度
如果 temperature=100?
dim_t = [1, 1.41, 2, ... 100] # 范围太窄,只能捕捉局部,无法建模全局关系问题2:32对 sin/cos 凭什么"够用"?
"远超常规图像需求"。
信息容量计算
64维编码空间理论上可区分 2⁶⁴ ≈ 1.8×10¹⁹ 个不同位置
即使考虑 sin/cos 的连续性,有效容量也 >> 10⁶
224×224=50,176 个像素的位置编码绰绰有余
工程验证
论文实验:在 1000×1000 以内的图像上效果良好
超过1000×1000? 需要增大
num_pos_feats或temperature结论 :32对编码是一种性价比权衡,对大多数视觉任务足够
问题3:dim_t 与粒度的推理逻辑
这是最核心的物理直觉
逻辑链(从数学到直觉)
pythondim_t 越小 → 波长 λ 越短 → 在固定坐标范围内振荡越快 → 对微小位置变化敏感 → 细粒度 dim_t 越大 → 波长 λ 越长 → 在固定坐标范围内振荡越慢 → 对微小位置变化鲁棒 → 粗粒度在 64×64 图像中的具体表现
dim_t 波长 λ 在 64 像素内经历周期数 ** 物理意义 ** ** 捕捉粒度 ** ** 1 ** 6.28 像素 ** 64/6.28 ≈ 10 周期 ** ** 每 6 像素重复一次 ** ** 超细:区分相邻像素 ** ** 10 ** 62.8 像素 ** 64/62.8 ≈ 1 周期 ** ** 整个图约 1 个波 ** ** 细:区分局部区域 ** ** 100 ** 628 像素 ** 64/628 ≈ 0.1 周期 ** ** 变化极缓慢 ** ** 粗:捕捉全局趋势 ** ** 1000 ** 6280 像素 ** 64/6280 ≈ 0.01 周期 ** ** 几乎不变 ** ** 超粗:编码极远关系 ** ** 图形化理解 **
# 像素位置: [0, 1, 2, 3, ..., 63] # dim_t=1 (λ≈6): sin([0, 1, 2, 3, ...]/1) = [0, 0.84, 0.91, 0.14, -0.76, ...] # ^^^ 剧烈振荡,相邻像素值差异大 # dim_t=100 (λ≈628): sin([0, 1, 2, 3, ...]/100) = [0, 0.01, 0.02, 0.03, ...] # ^^^ 缓慢变化,相邻像素几乎相同** 关键洞察 **:
** 高频(短波长)** = 差异放大器:对局部位置变化敏感
低频(长波长) = 平滑滤波器:提供全局位置基准
整体逻辑图
# 输入:像素位置矩阵 x_embed [B, H, W] # 每个像素的列坐标 (0~2π) # 步骤1:计算多尺度相位角 pos_x = x_embed[:, :, :, None] / dim_t[None, None, None, :] # 结果 [B, H, W, 32],每个像素得到32个不同波长下的相位 # 步骤2:sin/cos 编码 # dim_t=1 → 相位角变化快 → sin值剧烈振荡 → 捕捉像素级细节 # dim_t=1000 → 相位角变化慢 → sin值几乎不变 → 捕捉图像级全局位置 # 步骤3:拼接 y 方向 pos = torch.cat((pos_y, pos_x), dim=3) # 前32维是垂直位置,后32维是水平位置 # 最终:每个像素获得64维位置指纹,包含从6像素到6000像素的多尺度位置信息
一句话回答你的三个疑问
temperature=10000:让波长从 1 到 10,000 对数均匀分布,覆盖局部到全局32对编码够用:64维信息容量远超常规图像需求,是工程最优而非理论极限
dim_t 与粒度逻辑 :小 dim_t = 短波长 = 高频 = 区分近邻;大 dim_t = 长波长 = 低频 = 锚定全局
** 本质 :通过 多尺度波长 的叠加,让每个像素的位置编码同时包含" 我在局部很精确**"和"**我在全局有坐标**"的双重信息。
