无导数随机优化方法 是一类不依赖目标函数梯度信息 ,通过随机采样、迭代更新来寻找最优解的优化算法,
核心适用于梯度难以计算、不存在或计算成本极高的复杂优化场景。
本文综述了一种基于近似动态规划 ADP 的俄罗斯方块求解算法 CBMPI。
针对传统 ADP 依赖值函数 近似导致性能受限的问题,该算法创新性转向策略空间搜索,
通过 "采样 - 回归器 - 分类器 " 三步流程实现策略优化:
基于 m 步截断滚动 采样估计价值函数,利用最小二乘拟合回归器近似值函数,
借助 CMA-ES 优化分类器得到近似贪婪策略。
效果:在 20×10 大型棋盘上,CBMPI 平均消除 5100 万行,
首次使 ADP 类算法性能超越交叉熵(CE)方法,且样本用量仅为 CE 的 1/6,突破了传统ADP的局限性。
目录
[0. Motivaition:](#0. Motivaition:)
[1. 相关工作:](#1. 相关工作:)
[1.1 值函数算法](#1.1 值函数算法)
[1.2 描述棋盘的特征](#1.2 描述棋盘的特征)
[1.3 交叉熵方法 CEM](#1.3 交叉熵方法 CEM)
[1.4 noisy CE 玩 CartPole](#1.4 noisy CE 玩 CartPole)
[2. CBMPI 采样 + 回归器 + 分类器](#2. CBMPI 采样 + 回归器 + 分类器)
[3. 与其他方法的区别比较](#3. 与其他方法的区别比较)
0. Motivaition:
CE -> 直接学习策略参数 在Tetris 表现好 ;传统 ADP 算法几乎完全依赖 价值函数近似表现不好。
启发:采用在策略空间内搜索的 ADP 算法,而非传统的、在值函数空间内搜索的算法。
- 状态 :由当前棋盘布局 与正在下落的方块共同定义;
- 动作 :方块的所有可行旋转 角度与放置位置的组合;
- 奖励 :最大化该状态对应的游戏得分。
- 特性:状态 s 下执行动作 a 的 s' 和 r 是固定的。
1. 相关工作:
1.1 值函数算法与局限性
(如值迭代、λ-PI); 值函数空间 F 是一组用于近似 "状态价值函数v(s)" 的函数族。
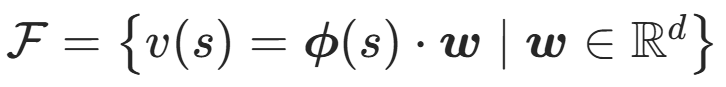
直接学值函数:
- 定义值函数的特征 ϕ(s)(比如最大列高度、各列高度、列高度差以及孔洞数量);
- 采样近似估计状态真实价值 v(s)
- 利用回归等方法 得到 ϕ(s) = v(s) * w;给状态打分
学习完值函数,可以进行贪心策略 转换为得分最高的状态:
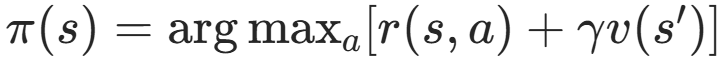
局限性是:如果值函数本身难以被值函数空间 F 准确表征,那么推导出来的策略性能会很差。
1.2 描述 Tetris 盘面的三种特征

-
Bertsekas:22个特征 棋盘孔洞数量、每列高度、相邻两列的高度差以及棋盘最大高度。
-
D-T特征:6 + 3 的特征(在后文的实验中最优)
-
高斯核 RBF 特征 exp (−|c−ih/4|²/(2 (h/5)²))
1.3 交叉熵方法 CEM
(Cross Entropy Method)找最优的均值和方差
每轮迭代 用现在的参数采样 n个样本,分别玩 L 把得到分数;
用排名前 ρ% 的参数的均值和方差,计算新的均值方差,进入下一轮迭代。

交叉熵 CE 参考学习文献:
Learning Tetris Using the Noisy Cross-Entropy Method 论文链接 带噪交叉熵(防止过早收敛)
A Tutorial on the Cross-Entropy Method Download PDF
1.4 noisy CE 玩 CartPole
4维状态 s(位置、速度、角度、角速度) -> 1 维动作 (向左还是向右推)
交叉熵学权重 w;再用 w与s的内积 决定动作。
- 玩一把 评估权重 w。
python
import gymnasium as gym
import numpy as np
def evaluation(env, W):
"""使用参数向量W为策略运行1个episode,返回该episode的奖励"""
reward_sum = 0
state, _ = env.reset()
while True:
action = int(np.dot(W, state) > 0) # w*s 内积决定动作
state, reward, terminated, truncated, info = env.step(action)
reward_sum += reward
if terminated or truncated:
break
return reward_sum- 利用均值和方差 产生一堆4维向量;随着步数衰减的噪声。
python
def init_params(mu, sigma, n):
"""使用均值向量mu和标准差向量sigma创建参数矩阵"""
m = mu.shape[0]
w_matrix = np.zeros((n, m)) # 行数为样本数 列数为w维度
for p in range(m): # 每列正态分布
w_matrix[:, p] = np.random.normal(
loc=mu[p], # 均值
scale=sigma[p] + 1e-17, # 标准差
size=(n,)
)
return w_matrix
def get_constant_noise(step):
"""随时间衰减的噪声"""
return np.maximum(5 - step / 10.0, 0)3. 迭代训练 生成 n 组权重 保留分数前 p 名的;并用前 p 的均值方差进入下一轮迭代。
python
n = 40 # 每代种群大小
p = 8 # 精英集大小
n_iter = 30 # 训练迭代次数
env = gym.make('CartPole-v1', render_mode=None) # 训练时
# 参数向量的均值(mu)和标准差(sigma) 对应状态空间维度
mu = np.random.uniform(size=env.observation_space.shape[0])
sigma = np.random.uniform(low=0.001, size=env.observation_space.shape[0])
for i in range(n_iter):
# 根据当前均值方差 初始化参数向量数组
w = init_params(mu, sigma, n)
# 评估每个参数向量
reward_sums = np.zeros(n)
for k in range(n):
reward_sums[k] = evaluation(env, w[k, :])
# 选取奖励最高的p个向量(精英集)
rankings = (np.argsort(reward_sums))[-p:] # 根据奖励对参数向量排序
top_vectors = w[rankings, :]
# 用精英集更新 均值和方差
for q in range(top_vectors.shape[1]):
mu[q] = top_vectors[:, q].mean()
sigma[q] = top_vectors[:, q].std() + get_constant_noise(i) # 方差加噪声
print("=" * 80)
print(f"iteration: {i}, mean reward: {reward_sums.mean():.2f}")
print(f"reward range: {reward_sums.min():.2f} to {reward_sums.max():.2f}\n")
if reward_sums.mean() > 480: # 算平均分+早停
print("Solved!")
break
env.close()- 测试最终的权重w。
python
# 测试最终的权重w
env_test = gym.make('CartPole-v1', render_mode="human") # 测试时human模式
print("\nTesting final policy...")
test_rewards, final_W = [], mu
print("parameters: ", final_W)
for test_ep in range(10):
# 使用最终的均值作为策略参数
reward = evaluation(env_test, final_W)
test_rewards.append(reward)
print(f"Test episode {test_ep + 1}: Reward = {reward}")
print(f"\nAverage test reward: {np.mean(test_rewards):.2f}")
env_test.close()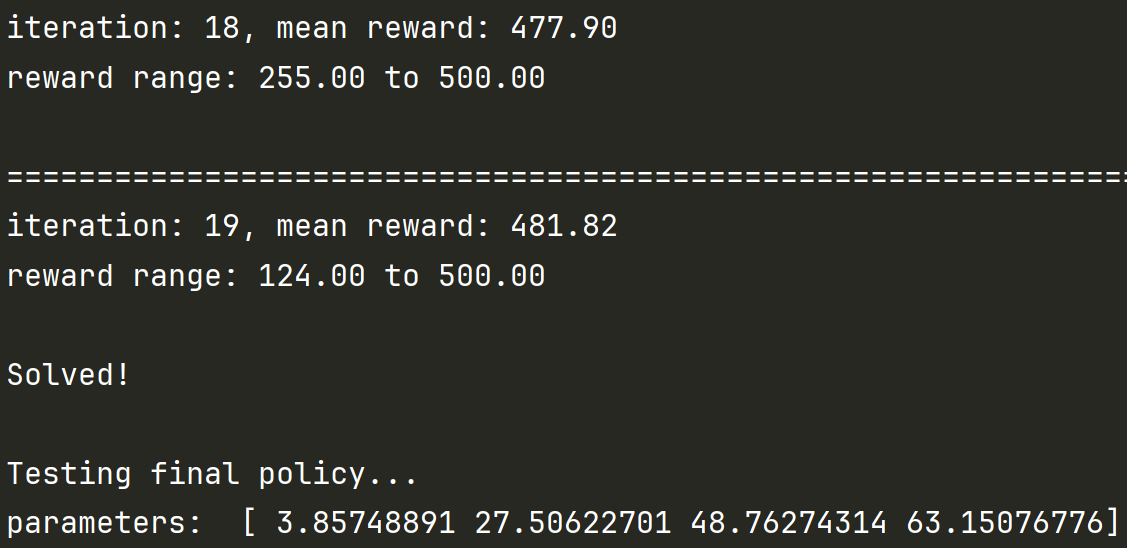

2. CBMPI 采样 + 回归器 + 分类器
输入:值函数空间 F (包含ϕ(s)值特征向量 )策略空间 Π (包含φ(s,a)动作特征向量)状态分布 µ
(这两个空间,再学习参数,和 DQN 之类的方法 差别很大)
-
rollouts 利用上一轮得到的 π 采样轨迹,近似 动作价值函数v(s) 和状态价值函数 Q(s,a);
-
回归器 根据状态的特征 回归 v(s);
-
分类器 利用 v(s) 学策略。
步骤1:rollouts 往后 m 步,用 π_k(s|a) 采样轨迹 (由上一轮迭代的步骤3得到)
得到 状态价值函数 V(s) 和 动作价值函数 Q(s,a) 的估计值。
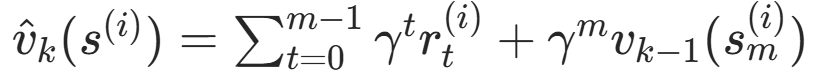
其中 m 步截断,m 步之后的价值 由上一次迭代的价值回归器 v_k-1(s_m) 得到。
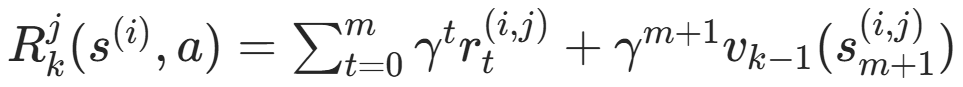
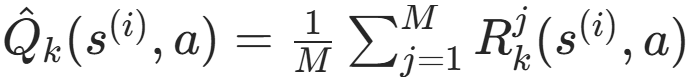
V(s) 和 Q(s,a) 本来需要分别采样 ,但为了效率更高 共用采样样本集D(实验发现效果并未下降)
步骤 2(回归器) :近似值函数,回归问题。
在值函数空间 F 中找一个函数 v_k,尽可能接近 "当前策略 π_k 对应的 m 步贝尔曼算子结果"。
(本文使用最小二乘 求解得系数 w )(这一部分衔接 相关工作中 值函数算法)
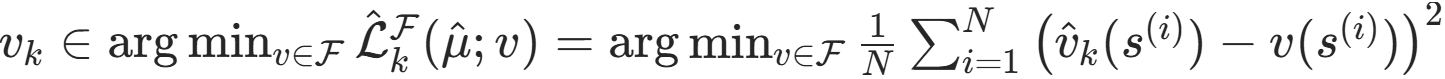
步骤 3(分类器) :近似贪婪策略。
在策略空间中找一个策略 π_{k+1} ,使得它尽可能接近 "基于当前值函数的最优贪婪策略"。
新的 π_{k+1} 在下一次迭代时 用于 rollouts。
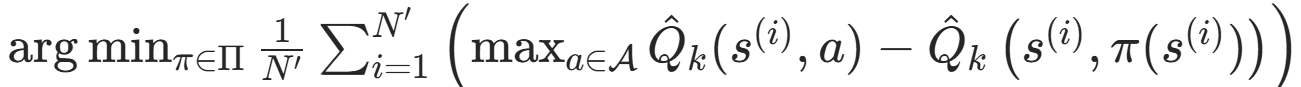
训练数据集为:动作空间大小为 |A|,则对于每个状态对应长度为 |A| 的向量,
为每个动作对应的 Q(s,a) 与 最优值差多少,Q(s,a) - max Q(s,a)。
状态 s 下的策略 π,依赖于策略参数权重 u ,是策略特征向量 φ(s,a) 的权重。
策略特征向量 φ(s,a) 和 值特征向量 ϕ(s) 都是盘面相关的特征表征。
u * φ(s,a) 对应分数最大的动作 a 即为 π(s) 的输出动作。
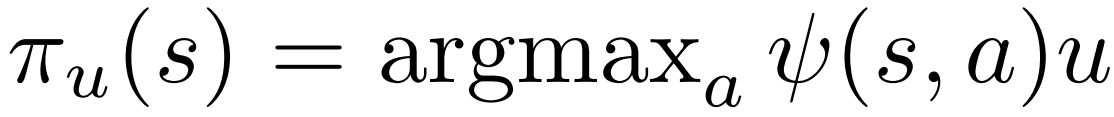
调权重 u :CMA-ES 协方差矩阵自适应进化策略
优势:在训练集已知的情况下 评估 u 只需计算经验误差,无需任何游戏模拟。
而交叉熵(CE )方法在策略评估 阶段,必须运行多局游戏才能完成评估。
故 相同效果的情况下,只需要CE 1/6 的样本用量。
3. 与其他方法的区别比较
此为 m 步截断:
m=1 则为经典值迭代 算法(从值函数推导策略,每一步都做 "一步贝尔曼更新");
m=∞ 则为策略迭代 算法(精确计算 当前策略的价值函数,相当于无限步贝尔曼更新)。
移除回归器 模块不拟合 v ,仅使用截断长度为 m 的滚动采样轨迹;则退化为 直接策略迭代(DPI)。
DPI 只看 m 步内的奖励 ,忽略 v(s_m);而 CBMPI 上一步的回归器 v_k-1 帮忙评估状态 s_m。
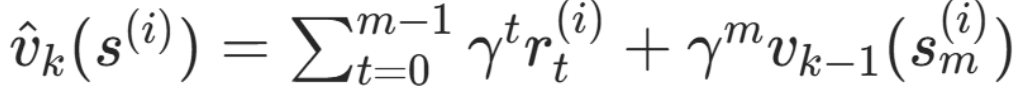
继承 CbPI 的核心思想:在策略空间中搜索 (而非从值函数推导策略),
避免传统 ADP "值函数 难以被值函数空间 F 准确表征" ,那么策略性能会很差 的局限性。
两个参考的 Tetris github 项目:
https://github.com/LoveDaisy/tetris_game
https://github.com/corentinpla/Learning-Tetris-Using-the-Noisy-Cross-Entropy-Method