在很多理论分析中,我们常常将神经网络的第一层统一抽象为:
Z=WX+b \mathbf{Z} = \mathbf{WX}+\mathbf{b} Z=WX+b
对于不同任务,这一抽象可能对应不同的具体实现: 在表格、语音或中间表示中,它往往就是显式的线性映射; 在视觉等具有空间结构的任务中,则常由卷积层实现。那么,当第一层采用卷积结构时,这种统一的线性写法是否仍然合理?在什么前提下成立?
本文尝试从结构展开 → 统计视角 → 理论分析适用性三个层次,系统回答这些问题。
一、问题的来源:为什么"卷积 ≈ 线性映射"?
在深度学习的数值分析与优化理论中,我们经常看到如下处理:
- 忽略卷积的空间结构
- 忽略权重共享带来的稀疏与重复
- 将第一层视为一次线性映射 z=Wx+bz = Wx + bz=Wx+b
这种写法并不是在"否认卷积结构的存在",而是基于一个更高层次的问题意识:我们真正关心的,是输入随机变量的统计特性,如何通过第一层被线性组合并传播。
要理解这一点,首先需要拆解:卷积的线性性究竟体现在哪里。
二、卷积的线性结构并非"一步完成"
以标准二维卷积为例。对于第 kkk 个输出通道,在空间位置 (u,v)(u,v)(u,v) 处,其计算为:
zk(u,v)=∑c=1C∑i,jWk,c,i,jXc(u+i,v+j)+bk z_k(u, v) = \sum_{c=1}^{C}\sum_{i,j}W_{k,c,i,j}X{_c}(u+i, v+j)+b_k zk(u,v)=c=1∑Ci,j∑Wk,c,i,jXc(u+i,v+j)+bk
可以看出,这一表达式清楚地表明:卷积本身是线性的。但更重要的是,它的线性性并不是一个"整体动作",而是由两个层次的线性操作组合而成。
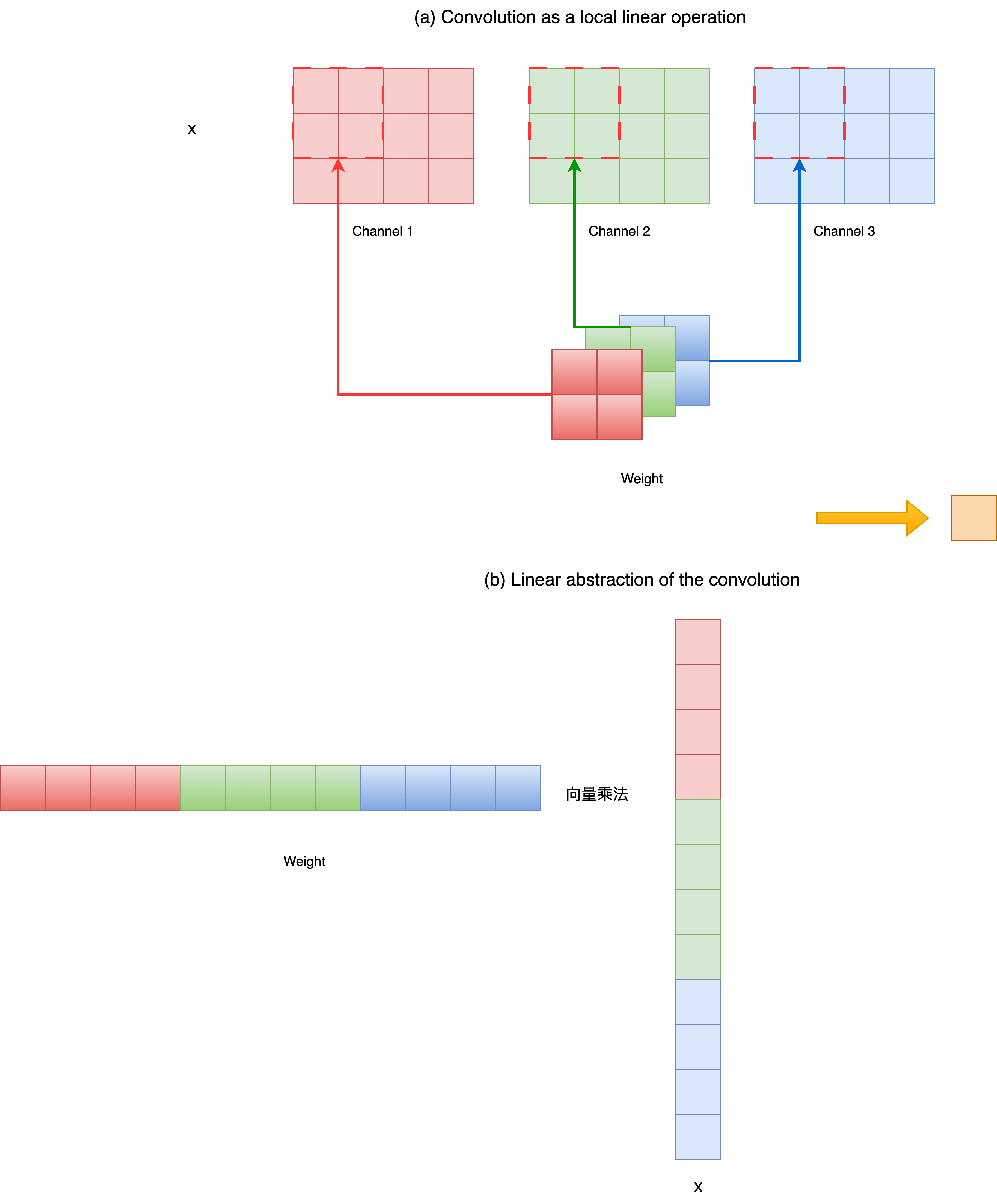
2.1 通道内的空间线性组合
对于固定的输入通道 xcx_cxc,在局部感受野 (i,j)(i,j)(i,j) 内,对空间位置的像素进行加权求和。这是一个局部空间向量与权重向量的内积。
从线性代数角度看,每一个空间窗口,都可以被展开为一个向量,与对应的卷积核权重做一次线性映射。
2.2 跨通道的线性叠加
在得到每个通道的空间响应后,不同输入通道的响应按通道权重再次进行加权求和。
这一步本质上是通道维度上的线性组合。
2.3 小结:卷积的线性性来自"结构组合"
因此,卷积层的线性性并不是「一次矩阵乘法」,而是:空间线性 + 通道线性 的组合结果。
这一点在实现层面非常重要,但在统计分析层面,恰恰为进一步抽象创造了条件。
三、从结构线性到统计等价
在很多理论分析中(尤其是初始化与 Normalize 相关讨论),我们往往刻意不区分以下因素:不同空间位置、不同卷积核尺寸、权重共享所带来的稀疏结构。
原因并不是这些因素不重要,而是:它们并不改变线性组合对随机变量统计量的传播方式。
3.1 空间窗口作为高维随机向量
从概率视角看,一个局部感受野内的输入,可以被视为一个高维随机向量 x∈Rdx \in \mathbb{R}^dx∈Rd。
无论这个向量来自:图像的一个 patch、或者特征图的一个窗口,只要操作是:
z=WTX+b z = \mathbf{W}^T\mathbf{X}+b z=WTX+b
那么,E[z]\mathbb{E}[z]E[z],Var(z)\mathrm{Var}(z)Var(z)的计算方式,只依赖于线性加权结构本身。
3.2 显式矩阵 vs. 隐式结构
因此,在统计意义上是先做空间卷积、再做通道求和,还是将整个窗口展开为向量、做一次矩阵乘法是等价的。
- 区别只存在于:
- 参数共享方式
- 计算效率
- 表达结构约束
- 而不体现在:均值、方差、尺度如何传播。
4. 为什么这种抽象对 Normalize 分析是充分的?
Normalize(如 transforms.Normalize、BatchNorm 前的输入归一化)直接作用于:各通道输入随机变量的均值和各通道输入随机变量的方差尺度。
关键问题是这些统计量,如何通过第一层被放大、缩小或失衡?
4.1 Normalize 只关心"线性响应"
设输入随机向量x∈Rd\mathbf{x} \in \mathbb{R}^dx∈Rd ,其均值与协方差分别为:
E[x],Var(x) \mathbb{E}[\mathbf{x}], \quad \mathrm{Var}(\mathbf{x}) E[x],Var(x)
其中,x\mathbf{x}x 是一个 ddd 维随机向量,表示输入的 ddd 个随机变量(例如图像的 ddd 个像素或特征维度)。因此,E[x]∈Rd\mathbb{E}[\mathbf{x}] \in \mathbb{R}^dE[x]∈Rd 是均值向量,每个分量 E[xi]\mathbb{E}[x_i]E[xi] 表示对应输入维度的期望。 Var(x)∈Rd×d\mathrm{Var}(\mathbf{x}) \in \mathbb{R}^{d \times d}Var(x)∈Rd×d 是协方差矩阵,用来描述各输入维度之间的方差及协方差。
当对 x\mathbf{x}x 施加线性变换 Wx+bW \mathbf{x} + \mathbf{b}Wx+b 时,输出的均值与方差可以用这些统计量直接计算。
- 第一层的线性映射写为:
z=Wx+b \mathbf{z} = W \mathbf{x} + \mathbf{b} z=Wx+b
其中,WWW 表示权重矩阵(或等价的线性算子),b\mathbf{b}b 为偏置项。卷积层也可被抽象为受结构约束的线性算子 WWW。
(1) 输出的均值
由于期望算子对线性运算具有可交换性,有:
E[z]=E[Wx+b]=E[Wx]+E[b]=W E[x]+b \begin{align} \mathbb{E}[\mathbf{z}] &= \mathbb{E}[W \mathbf{x} + \mathbf{b}] \\ &= \mathbb{E}[W \mathbf{x}] + \mathbb{E}[\mathbf{b}] \\ &= W \, \mathbb{E}[\mathbf{x}] + \mathbf{b} \end{align} E[z]=E[Wx+b]=E[Wx]+E[b]=WE[x]+b
可以看到,输出均值仅由输入均值经过线性变换得到,与WWW的具体结构形式(卷积或全连接)无关。偏置bbb仅平移均值,不影响方差传播。
-
推导过程
-
根据期望的线性性质:
E[z]=E[Wx+b] \mathbb{E}[\mathbf{z}] = \mathbb{E}[W\mathbf{x}+\mathbf{b}] E[z]=E[Wx+b] -
期望对加法可分配:
E[Wx+b]=E[Wx]+E[b] \mathbb{E}[W\mathbf{x}+\mathbf{b}] =\mathbb{E}[W\mathbf{x}]+\mathbb{E}[\mathbf{b}] E[Wx+b]=E[Wx]+E[b] -
偏置bbb是常数向量,所以E[b]=b\mathbb{E}[\mathbf{b}] = \mathbf{b}E[b]=b:
E[Wx]+E[b]=E[Wx]+b \mathbb{E}[W\mathbf{x}]+\mathbb{E}[\mathbf{b}] = \mathbb{E}[W\mathbf{x}]+\mathbf{b} E[Wx]+E[b]=E[Wx]+b -
期望对线性算子可交换:
E[Wx]=WE[x] \mathbb{E}[W\mathbf{x}]=W\mathbb{E}[\mathbf{x}] E[Wx]=WE[x] -
最终得到:
E[z]=WE[x]+b \mathbb{E}[\mathbf{z}] = W\mathbb{E}[\mathbf{x}]+\mathbf{b} E[z]=WE[x]+b
-
(2) 输出的方差
输出方差的定义如下:
Var(z)=E[(z−E[z])(z−E[z])T] \mathrm{Var}(\mathbf{z}) = \mathbb{E}\Big[(\mathbf{z} - \mathbb{E}[\mathbf{z}]) (\mathbf{z} - \mathbb{E}[\mathbf{z}])^T \Big] Var(z)=E[(z−E[z])(z−E[z])T]
代入z=WX+bz = WX+bz=WX+b:
z−E[z]=(Wx+b)−(WE[x]+b)=W(x−E[x]) \mathbf{z}-\mathbb{E}[\mathbf{z}] = (W\mathbf{x}+\mathbf{b})-(W\mathbb{E}[\mathbf{x}]+\mathbf{b})= W(\mathbf{x}-\mathbb{E}[\mathbf{x}]) z−E[z]=(Wx+b)−(WE[x]+b)=W(x−E[x])
可以看出偏置b\mathbf{b}b在减去均值后消掉了,所以不影响方差。
所以:
Var(z)=E[(W(x−E[x]))(W(x−E[x]))T] \mathrm{Var}(\mathbf{z}) = \mathbb{E} \Big[ (W (\mathbf{x} - \mathbb{E}[\mathbf{x}])) (W (\mathbf{x} - \mathbb{E}[\mathbf{x}]))^T \Big] Var(z)=E[(W(x−E[x]))(W(x−E[x]))T]
利用矩阵乘法规则:
(W(x−E[x]))(W(x−E[x]))T=W[(x−E[x])(x−E[x])T]WT (W (\mathbf{x} - \mathbb{E}[\mathbf{x}])) (W (\mathbf{x} - \mathbb{E}[\mathbf{x}]))^T = W[(\mathbf{x}-\mathbb{E}[\mathbf{x}])(\mathbf{x}-\mathbb{E}[\mathbf{x}])^T] W^T (W(x−E[x]))(W(x−E[x]))T=W[(x−E[x])(x−E[x])T]WT
而E[(x−E[x])(x−E[x])T]=Var(x)\mathbb{E}[ (\mathbf{x} - \mathbb{E}[\mathbf{x}]) (\mathbf{x} - \mathbb{E}[\mathbf{x}])^T] = \mathrm{Var}(\mathbf{x})E[(x−E[x])(x−E[x])T]=Var(x),所以得到:
Var(z)=WVar(x)WT \mathrm{Var}(\mathbf{z}) = W \mathrm{Var}(\mathbf{x})W^T Var(z)=WVar(x)WT
这表明,输出方差由输入方差在权重算子下的线性变换决定。无论WWW来源于显式全连接矩阵还是卷积展开,形式都是一致的。
4.2 与初始化和梯度稳定性的关系
这正是为什么在分析Xavier / Kaiming 初始化的隐含假设:输入尺度失衡对激活分布的影响、梯度在前几层是否稳定传播时,可以放心地将:卷积层等价视为一个"带结构约束的线性映射"。
因为这种抽象:
- 不损失统计正确性
- 显著降低分析复杂度
- 使 Normalize 的作用机制一目了然
五、总结
-
卷积层本质上是线性的,但其线性性来自空间与通道两个层次的组合
-
在统计分析视角下,卷积与全连接的差异并不影响均值、方差与尺度传播规律
-
Normalize 只改变输入随机变量的统计属性,而这些属性的传播只依赖线性结构本身
-
因此,在初始化与稳定性分析中,将卷积层抽象为 z=Wx+b\mathbf{z} = W\mathbf{x}+ \mathbf{b}z=Wx+b 是合理且充分的
如果说实现层面的卷积是"结构化计算",那么在理论分析中,它完全可以被看作:**一个受约束的线性算子。**这正是理论与工程之间最常见、也最容易被误解的一次"视角切换"。